Saltar al contenido principal
LibreTexts Español

14.6E: Ejercicios para la Sección 14.6

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    116210

    • Edwin “Jed” Herman & Gilbert Strang
    • OpenStax
    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    En el ejercicio 1, encuentra la derivada direccional utilizando únicamente la definición de límite.

    1) a.\( f(x,y)=5−2x^2−\frac{1}{2}y^2\) en el punto\( P(3,4)\) en la dirección de\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Responder
    a.\( D_{\vecs u}f(3,4) =−8\sqrt{2}\)

    1) b.\( f(x,y)=y^2\cos(2x)\) en el punto\( P(\frac{π}{3},2)\) en la dirección de\(\vecs u=(\cos\frac{π}{4})\,\hat{\mathbf i}+(\sin\frac{π}{4})\,\hat{\mathbf j}\)

    Responder
    b.\( D_{\vecs u}f(\frac{π}{3},2) =−2\sqrt{6}-\sqrt{2}\)

    2) Encontrar la derivada direccional de\( f(x,y)=y^2\sin(2x)\) en el punto\( P(\frac{π}{4},2)\) en la dirección de\(\vecs u=5\,\hat{\mathbf i}+12\,\hat{\mathbf j}\).

    En los ejercicios 3 - 13, encontrar la derivada direccional de la función en la dirección de\(\vecs v\) como una función de\(x\) y\(y\). Recuerda que primero necesitas encontrar un vector unitario en la dirección del vector de dirección. Luego encuentra el valor de la derivada direccional en el punto\(P\).

    3)\( f(x,y)=xy, \quad P(-2,0), \quad \vecs v=\frac{1}{2}\,\hat{\mathbf i}+\frac{\sqrt{3}}{2}\,\hat{\mathbf j}\)

    Responder
    \(D_{\vecs v}f(x, y) = \frac{1}{2}y + \frac{\sqrt{3}}{2}x \)
    \(D_{\vecs v}f(-2, 0) = −\sqrt{3}\)

    4)\( h(x,y)=e^x\sin y,\quad P(1,\frac{π}{2}),\quad \vecs v=−\,\hat{\mathbf i}\)

    5)\( f(x,y)=x^2y,\quad P(−5,5),\quad \vecs v=3\,\hat{\mathbf i}−4\,\hat{\mathbf j}\)

    Responder
    \(D_{\vecs v}f(x, y) = \frac{6}{5}xy - \frac{4}{5}x^2 \)
    \(D_{\vecs v}f(-5,5)= -50\)

    6)\( f(x,y)=xy,\quad P(1,1), \quad \vecs u=⟨\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}⟩\)

    7)\( f(x,y)=x^2−y^2, \quad P(1,0), \quad \vecs u=⟨\frac{\sqrt{3}}{2},\frac{1}{2}⟩\)

    Responder
    \(D_{\vecs u}f(x, y) = x\sqrt{3} - y \)
    \(D_{\vecs u}f(1,0)= \sqrt{3}\)

    8)\( f(x,y)=3x+4y+7,\quad P(0,\frac{π}{2}), \quad \vecs u=⟨\frac{3}{5},\frac{4}{5}⟩\)

    9)\( f(x,y)=e^x\cos y,\quad P=(0,\frac{π}{2}), \quad \vecs u=⟨0,5⟩\)

    Responder
    \(D_{\vecs u}f(x, y) = -e^x\sin y \)
    \(D_{\vecs u}f(0, \frac{π}{2})= −1\)

    10)\( f(x,y)=y^{10},\quad \vecs u=⟨0,−3⟩,\quad P=(1,−1)\)

    11)\( f(x,y)=\ln(x^2+y^2),\quad \vecs u=⟨2,-5⟩,\quad P(1,2)\)

    Responder
    \(D_{\vecs u}f(x, y) = \frac{\sqrt{29}}{29}\left( \dfrac{4x-10y}{x^2 +y^2}\right) \)
    \(D_{\vecs u}f(1,2)= -\frac{16\sqrt{29}}{145}\)

    12)\( h(x,y,z)=xyz, \quad P(2,1,1),\quad \vecs v=2\,\hat{\mathbf i}+\,\hat{\mathbf j}−\,\hat{\mathbf k}\)

    Responder
    \( D_{\vecs v}h(x, y, z) = \frac{\sqrt{6}}{6}(2yz + xz - xy)\)
    \( D_{\vecs v}h(2,1,1) = \frac{2}{\sqrt{6}} = \frac{\sqrt{6}}{3}\)

    13)\( f(x,y,z)=y^2+xz,\quad P(1,2,2),\quad \vecs v=⟨2,−1,2⟩\)

    Contestar
    \( D_{\vecs v}f(x, y, z) = \frac{2}{3}(z - y + x)\)
    \(D_{\vecs v}f(1,2,2)= \frac{2}{3}\)

    En los ejercicios 14 - 19, encuentra la derivada direccional de la función en la dirección del vector unitario\(\vecs u=\cos θ \,\hat{\mathbf i}+\sin θ \,\hat{\mathbf j}.\)

    14)\( f(x,y)=x^2+2y^2,\quad θ=\frac{π}{6}\)

    15)\( f(x,y)=\dfrac{y}{x+2y},\quad θ=−\frac{π}{4}\)

    Contestar
    \( D_{\vecs u}f(x,y) = \dfrac{−\sqrt{2}(x+y)}{2(x+2y)^2}\)

    16)\( f(x,y)=\cos(3x+y),\quad θ=\frac{π}{4}\)

    17)\( w(x,y)=ye^x,\quad θ=\frac{π}{3}\)

    Contestar
    \( D_{\vecs u}f(x,y) = \dfrac{e^x(y+\sqrt{3})}{2}\)

    18)\( f(x,y)=x\arctan(y),\quad θ=\frac{π}{2}\)

    19)\( f(x,y)=\ln(x+2y),\quad θ=\frac{π}{3}\)

    Contestar
    \( D_{\vecs u}f(x,y) = \dfrac{1+2\sqrt{3}}{2(x+2y)}\)

    En los ejercicios 20 - 23, encuentra el gradiente\(\vecs \nabla f\).

    20) Encuentra el gradiente de\( f(x, y) = 3x^2 + y^3 - 3x + y\). Entonces encuentra su valor en el punto\(P(2,3)\).

    21) Encuentra el gradiente de\( f(x,y)=\dfrac{14−x^2−y^2}{3}\). Después, encuentra el gradiente en el punto\( P(1,2)\).

    Contestar
    \( \vecs \nabla f(x, y) = -\frac{2}{3}x\,\hat{\mathbf i} -\frac{2}{3}y\,\hat{\mathbf j}\)
    \( \vecs \nabla f(1,2) = -\frac{2}{3}\,\hat{\mathbf i} -\frac{4}{3}\,\hat{\mathbf j}\)

    22) Encuentra el gradiente de\( f(x,y)=\ln(4x^3 - 3y)\). Después, encuentra el gradiente en el punto\( P(1,1)\).

    23) Encuentra el gradiente de\( f(x,y,z)=xy+yz+xz\). Luego encuentra el gradiente en el punto\( P(1,2,3).\)

    Contestar
    \( \vecs \nabla f(x, y, z) = ⟨y+z, x+z, y + x⟩\)
    \( \vecs \nabla f(1,2,3) = ⟨5,4,3⟩\)

    En los ejercicios 24 - 25, encuentra la derivada direccional de la función en el punto\( P\) en la dirección de\( Q\).

    24)\( f(x,y)=x^2+3y^2,\quad P(1,1),\quad Q(4,5)\)

    25)\( f(x,y,z)=\dfrac{y}{x+z},\quad P(2,1,−1),\quad Q(−1,2,0)\)

    Contestar
    \( D_{\vecd{PQ}}f(x,y) = \frac{3}{\sqrt{11}}\)

    26) Encontrar la derivada direccional de\( f(x,y,z))\) en\( P\) y en la dirección de\( \vecs u: \quad f(x,y,z)=\ln(x^2+2y^2+3z^2),\quad P(2,1,4),\quad \vecs u=\frac{−3}{13}\,\hat{\mathbf i}−\frac{4}{13}\,\hat{\mathbf j}−\frac{12}{13}\,\hat{\mathbf k}\).

    En los ejercicios 27 - 29, encuentra la derivada direccional de la función\( P\) en la dirección de\(\vecs u\).

    27)\( f(x,y)=\ln(5x+4y),\quad P(3,9),\quad \vecs u=6\,\hat{\mathbf i}+8\,\hat{\mathbf j}\)

    Contestar
    \( D_{\vecs u}f(3,9) = \frac{31}{255}\)

    28)\( f(x,y)=−7x+2y,\quad P(2,−4),\quad \vecs u=4\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    29)\( f(x,y,z)=4x^5y^2z^3,\quad P(2,−1,1),\quad \vecs u=\frac{1}{3}\,\hat{\mathbf i}+\frac{2}{3}\,\hat{\mathbf j}−\frac{2}{3}\,\hat{\mathbf k}\)

    Contestar
    \( D_{\vecs u}f(2,-1,1) = -320\)

    30) [T] Utilice la tecnología para bosquejar la curva de nivel\( f(x,y)=4x−2y+3\) que pasa a través\( P(1,2)\) y dibujar el vector de gradiente en\( P\).

    31) [T] Utilice la tecnología para bosquejar la curva de nivel\( f(x,y)=x^2+4y^2\) que pasa a través\( P(−2,0)\) y dibujar el vector de gradiente en\(P\).

    Contestar
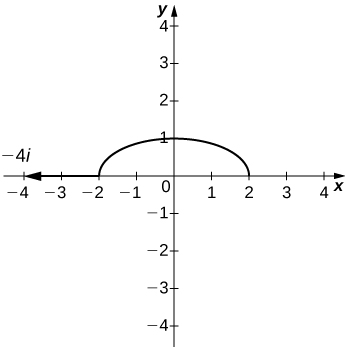
    Croquis de la curva de nivel de f (x, y) =x^2+4y^2 que pasa por P (−2,0) y mostrando el vector de gradiente en P.

    En los ejercicios 32 - 35, encuentra el vector de gradiente en el punto indicado.

    32)\( f(x,y)=xy^2−yx^2,\quad P(−1,1)\)

    33)\( f(x,y)=xe^y−\ln(x),\quad P(−3,0)\)

    Contestar
    \(\vecs \nabla f(-3,0) = \frac{4}{3}\,\hat{\mathbf i}−3\,\hat{\mathbf j}\)

    34)\( f(x,y,z)=xy−\ln(z),\quad P(2,−2,2)\)

    35)\( f(x,y,z)=x\sqrt{y^2+z^2}, \quad P(−2,−1,−1)\)

    Contestar
    \(\vecs \nabla f(-2,-1,-1) = \sqrt{2}\,\hat{\mathbf i}+\sqrt{2}\,\hat{\mathbf j}+\sqrt{2}\,\hat{\mathbf k}\)

    En los ejercicios 36 - 40, encuentra la derivada direccional indicada de la función.

    36)\( f(x,y)=x^2+xy+y^2\) en el punto\( (−5,−4)\) en la dirección en que la función aumenta más rápidamente.

    37)\( f(x,y)=e^{xy}\) en el punto\( (6,7)\) en la dirección en que la función aumenta más rápidamente.

    Contestar
    \( 1.6(10^{19})\)

    38)\( f(x,y)=\arctan\left(\dfrac{y}{x}\right)\) en el punto\( (−9,9)\) en la dirección en que la función aumenta más rápidamente.

    39)\( f(x,y,z)=\ln(xy+yz+zx)\) en el punto\( (−9,−18,−27)\) en la dirección en que la función aumenta más rápidamente.

    Contestar
    \( \frac{5\sqrt{2}}{99}\)

    40)\( f(x,y,z)=\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\) en el punto\( (5,−5,5)\) en la dirección en que la función aumenta más rápidamente.

    En los ejercicios 41 - 43, encuentra la tasa máxima de cambio de\( f\) en el punto dado y la dirección en la que ocurre.

    41)\( f(x,y)=xe^{−y}, \quad (-2,0)\)

    Contestar
    \(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \sqrt{5}, \quad ⟨1,2⟩\)
    Solución:
    \( \vecs \nabla f(x, y) = e^{-y} \mathbf{\hat i} - xe^{-y} \mathbf{\hat j}.\)Entonces\(\text{max}\big\{D_{\vecs u} f(-2,0)\big\} = \|\vecs \nabla f(-2, 0)\| = \sqrt{5}.\)
    La dirección en la que ocurre será solo la dirección del vector de gradiente:\(\vecs \nabla f(-2, 0) = ⟨1,2⟩.\)

    42)\( f(x,y)=\sqrt{x^2+2y}, \quad (4,10)\)

    43)\( f(x,y)=\cos(3x+2y),\quad (\frac{π}{6},−\frac{π}{8})\)

    Contestar
    \( \text{max}\big\{D_{\vecs u} f\left(\frac{π}{6},−\frac{π}{8}\right)\big\} = \sqrt{\frac{13}{2}} = \frac{\sqrt{26}}{2},\quad ⟨−3,−2⟩\)

    En los ejercicios 44 - 47, encuentra ecuaciones de

    a. el plano tangente y

    b. la línea normal a la superficie dada en el punto dado.

    44) La curva de nivel\( f(x,y,z)=12\) para\( f(x,y,z)=4x^2−2y^2+z^2\) en el punto\( (2,2,2).\)

    45)\( f(x,y,z)=xy+yz+xz=3\) en el punto\( (1,1,1)\)

    Contestar
    a. ecuación del plano tangente:\(x+y+z=3\),
    b. ecuaciones de línea normal:\(x−1=y−1=z−1\)

    46)\( f(x,y,z)=xyz=6\) en el punto\( (1,2,3)\)

    47)\( f(x,y,z)=xe^y\cos z−z=1\) en el punto\( (1,0,0)\)

    Contestar
    a. ecuación del plano tangente:\(x+y−z=1\),
    b. ecuaciones de línea normal:\(x−1=y=−z\)

    En los ejercicios 48 - 51, resolver el problema planteado.

    48) La temperatura\( T\) en una esfera metálica es inversamente proporcional a la distancia desde el centro de la esfera (el origen:\( (0,0,0))\). La temperatura en el punto\( (1,2,2)\) es de\( 120\) °C.

    a. Encontrar la tasa de cambio de la temperatura en el punto\( (1,2,2)\) en la dirección hacia el punto\( (2,1,3).\)

    b. Demostrar que, en cualquier punto de la esfera, la dirección de mayor incremento de temperatura viene dada por un vector que apunta hacia el origen.

    49) El potencial eléctrico (voltaje) en una determinada región del espacio viene dado por la función\( V(x,y,z)=5x^2−3xy+xyz.\)

    a. Encontrar la tasa de cambio de la tensión en el punto\( (3,4,5)\) en la dirección del vector\( ⟨1,1,−1⟩.\)

    b. ¿En qué dirección cambia el voltaje más rápidamente en el punto\( (3,4,5)\)?

    c. ¿Cuál es la tasa máxima de cambio de la tensión en el punto\( (3,4,5)\)?

    Contestar
    a.\(\frac{32}{\sqrt{3}}\),
    b.\(⟨38,6,12⟩\),
    c.\(2\sqrt{406}\)

    50) Si el potencial eléctrico en un punto\( (x,y)\) en el\(xy\) plano es\( V(x,y)=e^{−2x}\cos(2y)\), entonces el vector de intensidad eléctrica at\( (x,y)\) es\( E=−\vecs \nabla V(x,y).\)

    a. Encuentra el vector de intensidad eléctrica en\( (\frac{π}{4},0).\)

    b. Demostrar que, en cada punto del plano, el potencial eléctrico disminuye más rápidamente en la dirección del vector\( E.\)

    51) En dos dimensiones, el movimiento de un fluido ideal se rige por un potencial de velocidad\( φ\). Los componentes de velocidad del fluido\(u\) en la dirección\(x\) - y\(v\) en la\(y\) dirección -dirección, están dados por\( ⟨u,v⟩=\vecs \nabla φ\). Encuentre los componentes de velocidad asociados con el potencial de velocidad\( φ(x,y)=\sin πx\sin 2πy.\)

    Contestar
    \( ⟨u,v⟩=⟨π\cos(πx)\sin(2πy),2π\sin(πx)\cos(2πy)⟩\)

    Colaboradores

    This page titled 14.6E: Ejercicios para la Sección 14.6 is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Edwin “Jed” Herman & Gilbert Strang (OpenStax) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.