14.8E: Ejercicios para la Sección 14.8

Última actualización
Guardar como PDF

Page ID: 116235

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1-15, utilice el método de multiplicadores Lagrange para encontrar los valores máximo y mínimo de la función sujeta a la restricción dada.

1) Función objetiva:$f(x, y) = 4xy$ Restricción:$\dfrac{x^2}{9} + \dfrac{y^2}{16} = 1$

Contestar: Sujeto a la restricción dada, la función$f$ tiene un mínimo relativo de$-24$ en ambos$ \left(-\frac{3\sqrt{2}}{2}, 2\sqrt{2}\right) $$ \left(\frac{3\sqrt{2}}{2}, -2\sqrt{2}\right) $ y y un máximo relativo de$24$ en ambos$ \left(\frac{3\sqrt{2}}{2}, 2\sqrt{2}\right) $ y$ \left(-\frac{3\sqrt{2}}{2}, -2\sqrt{2}\right) $

2) Función objetiva:$f(x, y) = x^2y$ Restricción:$x^2 + 2y^2 = 6$

3) Función objetiva:$f(x,y)=x^2 +y^2 +2x−2y+1$ Restricción:$ g(x,y)= x^2 +y^2 =2 $

Contestar: Sujeto a la restricción dada,$f$ tiene un mínimo relativo de$-1$ at$ (-1, 1) $ y un máximo relativo de$7$ at$ (1,-1) $.

4) Función objetiva:$f(x, y) = xy$ Restricción:$4x^2 + 8y^2 = 16$

5) Función objetiva:$f(x, y) = x^2 + y^2$ Restricción:$xy = 1$

Contestar: $f$tiene un mínimo relativo de$2$ en ambos$ (-1, -1) $ y$ (1,1) $, sujeto a la restricción dada.

6) Función objetiva:$f(x, y) = x^2 - y^2$ Restricción:$x−2y+6=0$

7) Función objetiva:$f(x, y) = x^2 + y^2$ Restricción:$x+2y−5=0$

Contestar: Sujeto a la restricción dada,$f$ tiene un mínimo relativo de$ f(1,2)=5$ en el punto$ (1, 2) $.

8) Función objetiva:$f(x, y) = x^2 + y^2$ Restricción:$(x−1)^2+4y^2=4$

9) Función objetiva:$f(x, y) = 4x^3 + y^2$ Restricción:$2x^2 + y^2 = 1$

Contestar: Sujeto a la restricción dada, la función$f$ tiene un mínimo relativo de$-\sqrt{2}$ at$ \left(-\frac{\sqrt{2}}{2}, 0\right) $,
un mínimo relativo de$\frac{25}{27}$ en ambos puntos$ \left(\frac{1}{3}, -\frac{\sqrt{7}}{3}\right) $ y$ \left(\frac{1}{3}, \frac{\sqrt{7}}{3}\right) $,
un máximo relativo de$\sqrt{2}$ at$ \left(\frac{\sqrt{2}}{2}, 0\right) $, y un máximo relativo de $1$en ambos puntos$ (0,1) $ y$ (0,-1) $.

Solución:: Dejar$g(x,y) = 2x^2 + y^2$ ser la función de restricción. Entonces:

$\vecs\nabla f(x,y) = 12x^2 \,\hat{\mathbf i} + 2y \,\hat{\mathbf j}$ y$\vecs\nabla g(x,y) = 4x \,\hat{\mathbf i} + 2y \,\hat{\mathbf j}$

Usando la ecuación del Multiplicador de Lagrange,\[\vecs\nabla f(x, y) = \lambda\vecs\nabla g(x, y),\nonumber \]
tenemos:\[12x^2 \,\hat{\mathbf i} + 2y \,\hat{\mathbf j} = 4x\lambda \, \hat{\mathbf i} + 2y\lambda \,\hat{\mathbf j}\nonumber \]
dándonos el sistema de ecuaciones:\[12x^2 = 4x\lambda, \quad 2y = 2y\lambda, \quad \text{and the constraint}\quad 2x^2 + y^2 = 1\nonumber \]
Reescribir el primero dos ecuaciones como cero productos (moviéndose a un lado y factorizando), obtenemos:
\[\begin{align*} 4x(3x - \lambda) &= 0 & \text{and} && 2y(1 - \lambda) &= 0 \\ x = 0 \quad \text{or}\quad \lambda &= 3x & & &y = 0 \quad \text{or}\quad \lambda &= 1 \end{align*}\]
Ahora consideramos las combinaciones de estas soluciones a las dos ecuaciones anteriores y conectamos cada una de ellas en la ecuación de restricción para resolver para los puntos Lagrange correspondientes.

La combinación$x = 0$ y$y = 0$ produce una contradicción cuando se coloca en la ecuación de restricción, ya que este punto no está en la elipse.

Tomando la combinación$x = 0$ y$\lambda = 1$, nos ponemos$0$$x$ en la restricción y resolvemos para$y$, obteniendo:$ y = \pm 1$. Esto nos da dos puntos Lagrange:$ (0, 1) $ y$ (0, -1)$.

Tomando la combinación$\lambda = 3x$ y$y = 0$, nos ponemos$0$$y$ en la restricción y resolvemos para$x$, obteniendo:$ x = \pm \frac{\sqrt{2}}{2}$. Esto nos da dos puntos Lagrange:$ \left(-\frac{\sqrt{2}}{2}, 0\right) $ y$ \left(\frac{\sqrt{2}}{2}, 0\right) $.

Tomando la combinación$\lambda = 3x$ y$\lambda = 1$, sustituimos$1$ en la primera ecuación por$\lambda$, dándonos$ 1 = 3x$ así$x = \frac{1}{3}$. Tapando este valor en para$x$ en la ecuación de restricción y resolviendo para$y$, obtenemos$y = \pm \frac{\sqrt{7}}{3}$ lo que nos da los dos puntos Lagrange:$ \left(\frac{1}{3}, -\frac{\sqrt{7}}{3}\right) $ y$ \left(\frac{1}{3}, \frac{\sqrt{7}}{3}\right) $.

Evaluando la función$f$ en estos puntos Lagrange, encontramos:\[\begin{align*} f(0, -1) &= 1 & f(0, 1) &= 1 \\ f\left(-\tfrac{\sqrt{2}}{2}, 0\right) &= \frac{-4(\sqrt{2})^3}{8} = -\sqrt{2} & f\left(\tfrac{\sqrt{2}}{2}, 0\right) &= \frac{4(\sqrt{2})^3}{8} = \sqrt{2} \\ f\left(\tfrac{1}{3}, -\tfrac{\sqrt{7}}{3}\right) &= \tfrac{25}{27} & f\left(\tfrac{1}{3}, \tfrac{\sqrt{7}}{3}\right) &= \tfrac{25}{27} \end{align*}\]

Comparando estos valores con donde se encuentran los puntos Lagrange correspondientes en la curva de restricción, concluimos los resultados establecidos en la respuesta arriba.

10) Función objetiva:$f(x,y)=2x^2 +y^2$ Restricción:$ g(x,y)= x^2 +y^2 =1 $

11) Función objetiva:$f(x,y,z)=x+3y−z$ Restricción:$ x^2+y^2+z^2=4 $

Contestar: Sujeto a la restricción dada,$f$ tiene un mínimo relativo de$-2\sqrt{11}$ en el punto$ \left(-\frac{2\sqrt{11}}{11}, \, -\frac{6\sqrt{11}}{11}, \, \frac{2\sqrt{11}}{11}\right) $ y un máximo relativo de$2\sqrt{11}$ en el punto$ \left(\frac{2\sqrt{11}}{11}, \, \frac{6\sqrt{11}}{11}, \, -\frac{2\sqrt{11}}{11}\right).$

12) Función objetiva:$f(x, y, z) = x + y + z$ Restricción:$\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1$

13) Función objetiva:$f(x, y, z) = xyz$ Restricción:$x^2+2y^2+3z^2=6$

Contestar: Sujeto a la restricción dada,$f$ tiene un mínimo relativo de$-\frac{2\sqrt{3}}{3}$ at$ \left( \sqrt{2},\, 1,\, -\frac{\sqrt{6}}{3} \right),\; \left( \sqrt{2},\, -1,\, \frac{\sqrt{6}}{3} \right),\; \left( -\sqrt{2},\, 1,\, \frac{\sqrt{6}}{3} \right),$$ \left( -\sqrt{2},\, -1,\, -\frac{\sqrt{6}}{3} \right) $ y y un máximo relativo de$\frac{2\sqrt{3}}{3}$ at$ \left( \sqrt{2},\, 1,\, \frac{\sqrt{6}}{3} \right),\; \left( \sqrt{2},\, -1,\, -\frac{\sqrt{6}}{3} \right),\; \left( -\sqrt{2},\, -1,\, \frac{\sqrt{6}}{3} \right),$ y$ \left( -\sqrt{2},\, 1,\, -\frac{\sqrt{6}}{3} \right) $.

14) Función objetiva:$f(x, y, z) = x^2 + y^2 + z^2$ Restricción:$x^4+y^4+z^4=1$

15) Función objetiva:$f(x, y, z) = x^2 + y^2 + z^2$ Restricción:$xyz=4$

Contestar: Sujeto a la restricción dada,$f$ tiene un mínimo relativo de$ 6\sqrt[3]{2}$ en los puntos$ \left(\sqrt[3]{4},\,\sqrt[3]{4},\,\sqrt[3]{4}\right),$$ \left(\sqrt[3]{4},\,-\sqrt[3]{4},\,-\sqrt[3]{4}\right),$$ \left(-\sqrt[3]{4},\,\sqrt[3]{4},\,-\sqrt[3]{4}\right),$ y$ \left(-\sqrt[3]{4},\,-\sqrt[3]{4},\,\sqrt[3]{4}\right).$
Para ver una visualización 3D de este problema, consulte: CalcPlot3D para Problema 15.

En los ejercicios 16-21, utilice el método de multiplicadores Lagrange para encontrar el extremo solicitado de la función dada sujeto a la restricción dada.

16) Maximizar$f(x,y) = \sqrt{6 - x^2 - y^2}$ sujeto a la restricción,$ x+y−2=0$.

17) Maximizar$f(x,y) = x^2 - y^2$ sujeto a las restricciones,$ g(x,y)=y−x^2=0, \quad x>0,\quad y>0$.

Contestar: Sujeto a las restricciones dadas,$f$ tiene un máximo relativo de$ f\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right)=\frac{1}{4}$ en el punto$ \left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right) $. Si no$x > 0$ fuera una restricción, habría habido otros dos puntos Lagrange con extremos relativos de$f$ sujeto a las otras dos restricciones. Estos habrían sido$ (0, 0) $ y$ \left(-\frac{\sqrt{2}}{2},\,\frac{1}{2}\right) .$

Para verificar que$f$ realmente tiene un máximo relativo en el punto$ \left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right), $ necesitaríamos verificar el valor de a cada$f$ lado de este punto en la curva de restricción,$y−x^2=0.$

Si$ x = 0.5$ cuál es menor que$\frac{\sqrt{2}}{2}$,$y$ sería$ y = (0.5)^2 = 0.25.$
Si$ x = 1$ cuál es mayor que$\frac{\sqrt{2}}{2}$,$y$ sería$ y = (1)^2 = 1.$

Entonces comparamos el valor de $f$en el punto Lagrange,$\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right)$, con los valores de$f$ en estos otros puntos en la restricción.
Tenemos$f(0.5, 0.25) = (0.5)^2 - (0.25)^2 = 0.25 - 0.0625 = 0.1875 < \frac{1}{4}$ y$f(1, 1) = (1)^2 - (1)^2 = 0 < \frac{1}{4}.$

por lo tanto, podemos concluir que$f$ efectivamente tiene un máximo relativo de$\frac{1}{4}$ en el punto$\left(\frac{\sqrt{2}}{2},\,\frac{1}{2}\right).$

18) Maximizar$U(x,y) = 8x^{4/5}y^{1/5}$ sujeto a la restricción,$ 4x+2y=12$.

19) Minimizar$f(x,y,z)=x^2+y^2+z^2$ sujeto a la restricción,$x+y+z=1$.

Contestar: Sujeto a la restricción dada,$f$ tiene un mínimo relativo de$ f\left(\frac{1}{3},\,\frac{1}{3},\,\frac{1}{3}\right)=\frac{1}{3}$ en el punto$ \left(\frac{1}{3},\,\frac{1}{3},\,\frac{1}{3}\right) $.

20) Minimizar$f(x,y)=xy$ en la elipse$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$.

21) Maximizar$f(x,y,z)=2x+3y+5z$ en la esfera$x^2+y^2+z^2=19$.

Contestar: Sujeto a la restricción dada,$f$ tiene un máximo relativo de$ 19\sqrt{2} $ en el punto$ \left( \sqrt{2},\, \frac{3\sqrt{2}}{2},\, \frac{5\sqrt{2}}{2} \right) $.
Obsérvese que, sujeto a esta restricción,$f$ también tiene un mínimo relativo de$ -19\sqrt{2} $ en el punto$ \left( -\sqrt{2},\, -\frac{3\sqrt{2}}{2},\, -\frac{5\sqrt{2}}{2} \right) $.
Para ver una visualización 3D de este problema, consulte: CalcPlot3D para Problema 21.

En los ejercicios 22-23, utilice el método de multiplicadores Lagrange con dos restricciones.

22) Optimizar$f(x,y,z)=yz+xy$ sujeto a las restricciones:$xy=1, \quad y^2+z^2=1$.

Contestar: máximo:$\frac{3}{2}$, mínimo:$\frac{1}{2}$

23) Minimizar$f(x,y,z)=x^2+y^2+z^2$ cuándo$x+y+z=9$ y$x+2y+3z=20$.

Contestar: mínimo:$f(2,3,4)=29$

Utilice el método de multiplicadores Lagrange para resolver los siguientes problemas aplicados.

24) Un recipiente grande en forma de sólido rectangular debe tener un volumen de 480 m ³. La parte inferior del contenedor cuesta $5/m ² para construir mientras que la parte superior y los lados cuestan $3/m ² para construir. Utilice multiplicadores Lagrange para encontrar las dimensiones del contenedor de este tamaño que tenga el costo mínimo.

25) Una caja rectangular sin tapa (una caja en topless) debe ser hecha de 12 pies ² de cartón. Encuentra el volumen máximo de una caja de este tipo.

Contestar: El volumen máximo es$4$ ft ³. Las dimensiones son$1×2×2$ ft.

26) Encuentra la distancia mínima de la parábola$y=x^2$ al punto$(0,3)$.

27) Encuentra el punto en la línea$y=2x+3$ que está más cerca del punto$(4,2)$.

Contestar: $ (25,195) $

29) Encuentra la distancia mínima del punto$(0,1)$ a la parábola$x^2=4y.$

Contestar: $1.0$unidad

30) Encuentra las distancias mínima y máxima entre la elipse$x^2+xy+2y^2=1$ y el origen.

31) Encuentra la distancia mínima del plano$x+y+z=1$ a punto$(2,1,1)$.

Contestar: $\sqrt{3}$unidades

32) Encuentra el punto en el plano$4x+3y+z=2 $ que está más cerca del punto$(1,−1,1)$.

33) Encuentra el punto en la superficie$x^2−2xy+y^2−x+y=0$ más cercano al punto$(1,2,−3).$

Contestar: $ \left(1,\,\frac{1}{2},\,−3\right) $

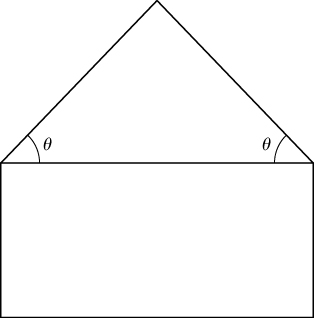
34) Un pentágono se forma colocando un triángulo isósceles sobre un rectángulo, como se muestra en el diagrama. Si el perímetro del pentágono es de 10 pulg., encuentra las longitudes de los lados del pentágono que maximizarán el área del pentágono.

$CNX_Calc_Figure_14_08_201.jpg$

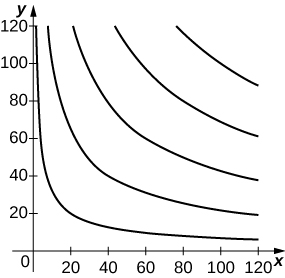
35) [T] Al invertir$x$ unidades de mano de obra y$y$ unidades de capital, un fabricante de relojes puede producir$P(x,y)=50x^{0.4}y^{0.6}$ relojes. Encuentre el número máximo de relojes que se pueden producir con un presupuesto de $20,000 si la mano de obra cuesta $100/unidad y los costos de capital $200/unidad. Utilice un grafo como CalcPlot3D para esbozar una gráfica de contorno de la función.

Contestar

Aproximadamente 3365 relojes en el punto crítico ($80,60).$

$Una serie de curvas en el primer cuadrante, con la primera comenzando cerca (2, 120), disminuyendo bruscamente a cerca (20, 20), y luego disminuyendo lentamente a (120, 5). La siguiente curva comienza cerca (10, 120), disminuye bruscamente a cerca (40, 40), y luego disminuye lentamente a (120, 20). La siguiente curva comienza cerca (20, 120), disminuye bruscamente a cerca (60, 60), y luego disminuye lentamente a (120, 40). La siguiente curva comienza cerca (40, 120), disminuye a cerca (80, 80), y luego disminuye un poco lentamente a (120, 60). La última curva comienza cerca de (60, 120) y disminuye de manera bastante uniforme a través de (100, 100) a (120, 90).$

36) Un sólido rectangular está contenido dentro de un tetraedro con vértices en$(1,0,0),\,(0,1,0),\,(0,0,1)$, y el origen. La base de la caja tiene dimensiones$x$ y$y$, y la altura de la caja es$z$. Si la suma de$x$,$y$, y$z$ es$1$, encontrar las dimensiones que maximizan el volumen del sólido rectangular.

37) Encuentra el valor máximo de$f(x,y)=\sin x\sin y,$ dónde$x$ y$y$ denota los ángulos agudos de un triángulo rectángulo. Dibuja la gráfica de superficie y la gráfica de contorno de la función usando un CAS.

Contestar: Sujeto a esta restricción,$f$ tiene un máximo relativo de$\frac{1}{2}$ cuándo$x = \frac{\pi}{4}$ y$y = \frac{\pi}{4}$.
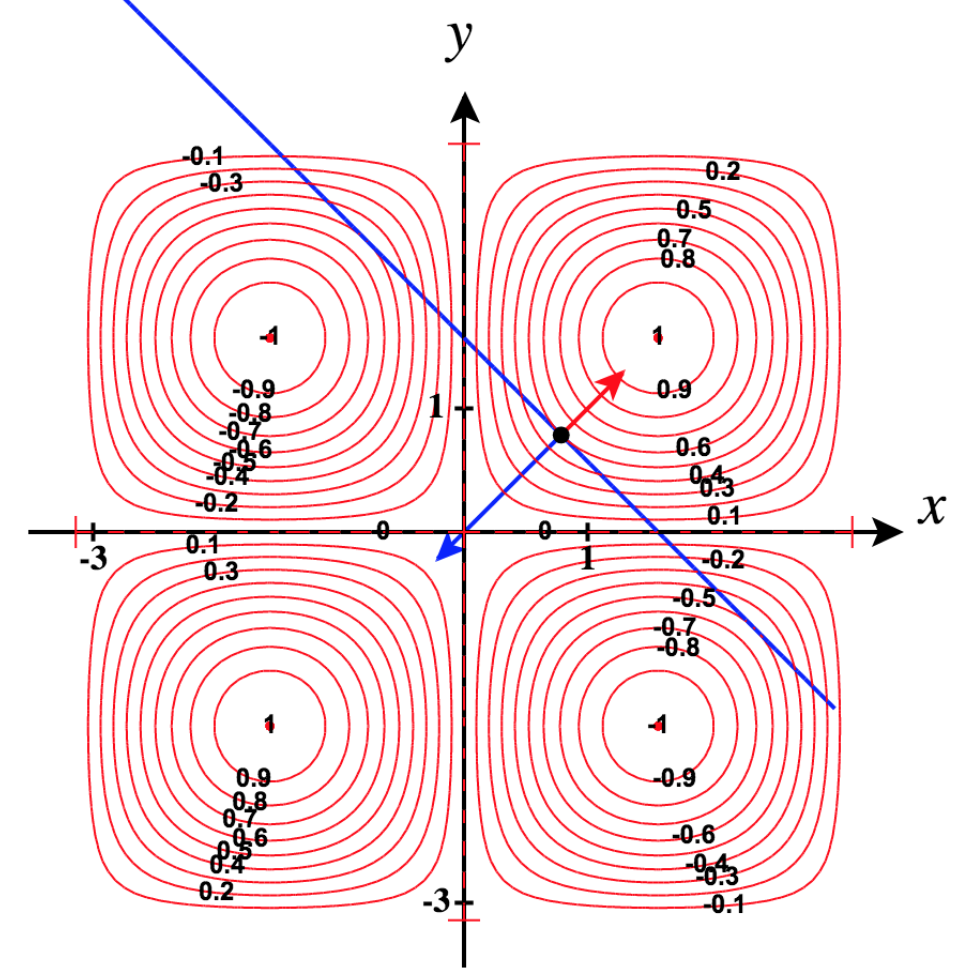
Trazado de superficie y trazado de contorno para$f$: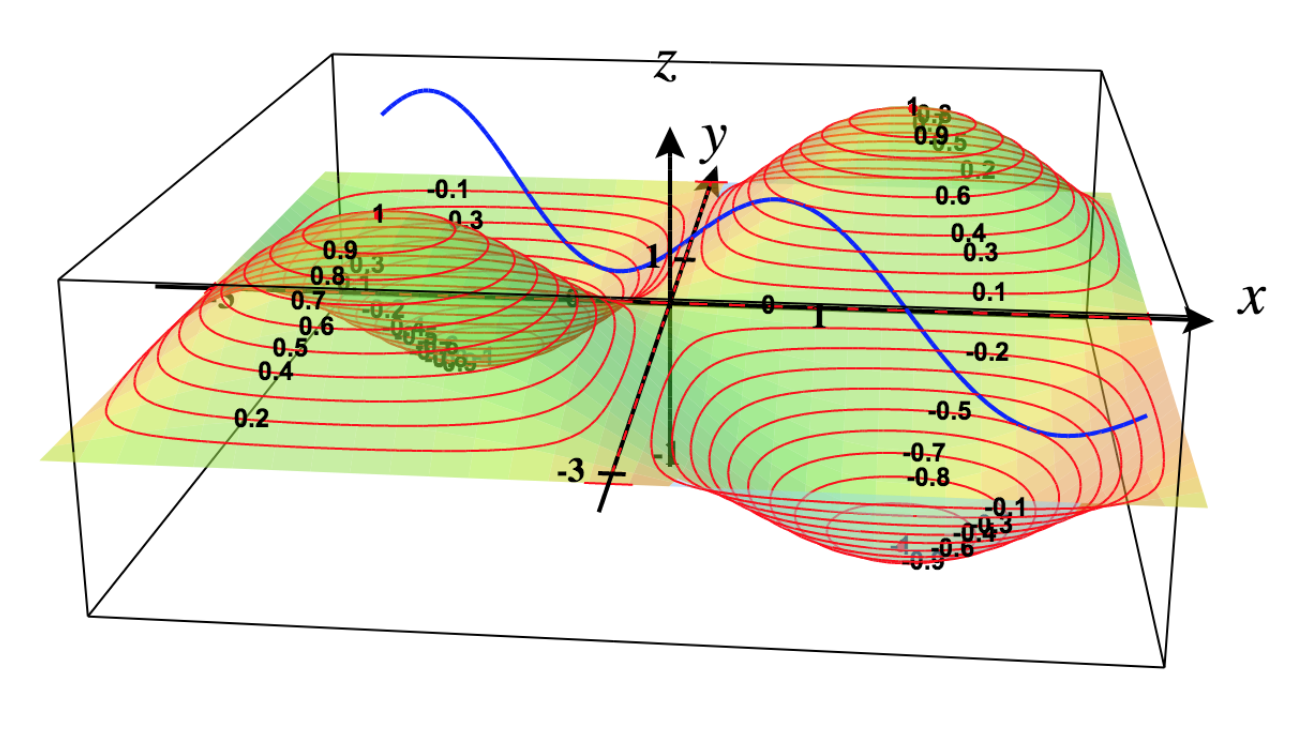
$Una serie alterna de colinas y valles de amplitud 1 a través del espacio xyz.$ $Gráfico de contorno para f (x, y) = sin x sin y$

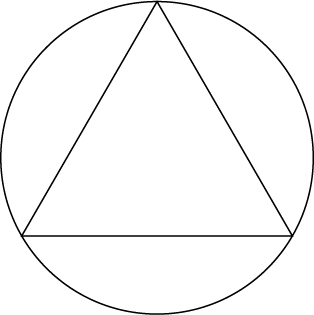
38) Mostrar que, de todos los triángulos inscritos en un círculo de radio$R$ (ver diagrama), el triángulo equilátero tiene el perímetro más grande.

$Un círculo con un triángulo equilátero dibujado dentro de él de tal manera que cada vértice del triángulo toca el círculo.$

Contributors

Template:ContribOpenStaxCalc
Paul Seeburger (Monroe Community College) reordered these problems, adding problems 3 and 10 and answers for problems 15 and 17. He also added a full worked-out solution for problem 9 and a link to CalcPlot3D in problems 15, 21 and 35. He also created new images for Problem 37 and expanded the answers for many problems.