14.9: Capítulo 14 Ejercicios de revisión

Última actualización
Guardar como PDF

Page ID: 116213

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Para los siguientes ejercicios, determinar si la afirmación es verdadera o falsa. Justifica tu respuesta con una prueba o un contraejemplo.

1. El dominio de$f(x,y)=x^3\arcsin(y)$ es$ \big\{ (x,y) \, | \, x \in \mathbb R\text{ and }−\pi≤y≤\pi \big\}.$

2. Si la función$f(x,y)$ es continua en todas partes, entonces$f_{xy}(x,y) =f_{yx}(x,y).$

Responder: Cierto, según el teorema de Clairaut

3. La aproximación lineal a la función de$f(x,y)=5x^2+x\tan y$ en el punto$(2,π)$ viene dada por$L(x,y)=22+21(x−2)+(y−π).$

4. $(34,916)$es un punto crítico de$g(x,y)=4x^3−2x^2y+y^2−2.$

Responder: Falso

Para los siguientes ejercicios, esboce la función en una gráfica y, en una segunda, esboce varias curvas de nivel.

5. $f(x,y)=e^{−\left(x^2+2y^2\right)}$

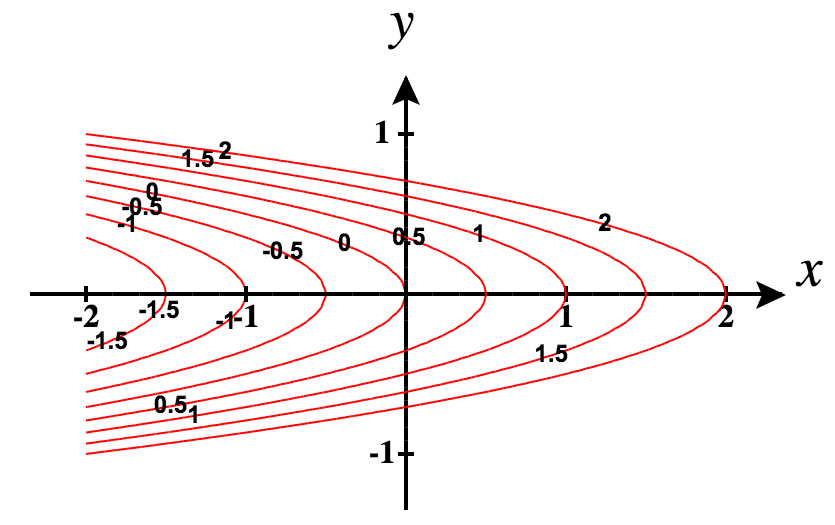
6. $f(x,y)=x+4y^2$

Responder: $Gráfica de Contorno para la función z = x + 4y^2$

Para los siguientes ejercicios, evalúe los siguientes límites, si existen. Si no existen, probarlo.

7. $\displaystyle \lim_{(x,y)→(1,1)}\frac{4xy}{x−2y^2}$

8. $\displaystyle \lim_{(x,y)→(0,0)}\frac{4xy}{x−2y^2}$

Responder: No existe.

Para los siguientes ejercicios, encuentra el mayor intervalo de continuidad para la función.

9. $f(x,y)=x^3\arcsin y$

10. $g(x,y)=\ln(4−x^2−y^2)$

Responder: Continuo en todos los puntos del$xy$ plano, excepto donde$x^2 + y^2 > 4.$

Para los siguientes ejercicios, encuentra todas las primeras derivadas parciales.

11. $f(x,y)=x^2−y^2$

12. $u(x,y)=x^4−3xy+1,$con$x=2t$ y$y=t^3$

Responder: $\dfrac{∂u}{∂x}=4x^3−3y,$

$ \dfrac{∂u}{∂y}=−3x,$

$\dfrac{dx}{dt} = 2$y$\dfrac{dy}{dt} = 3t^2$

\ (\ comenzar {alinear*}\ dfrac {du} {dt} &=\ dfrac {u} {x}\ cdot\ dfrac {dx} {dt} +\ dfrac {u} {y}\ cdot\ dfrac {dy} {dt}\\ [4pt]
&= 8x^3-6y -9xt^2\\ [4pt]
&= 8\ grande (2t\ grande) ^3 - 6 (t^3) - 9 (2t) t^2\\ [4pt]
&= 64t^3 - 6t^3 - 18t^3\\ [4pt]
&= 40t^3\ final {align*}\)

Para los siguientes ejercicios, encuentra todas las segundas derivadas parciales.

13. $g(t,x)=3t^2−\sin(x+t)$

14. $h(x,y,z)=\dfrac{x^3e^{2y}}{z}$

Responder: $h_{xx}(x,y,z) = \dfrac{6xe^{2y}}{z},$
$h_{xy}(x,y,z) = \dfrac{6x^2e^{2y}}{z},$
$h_{xz}(x,y,z) = −\dfrac{3x^2e^{2y}}{z^2},$
$h_{yx}(x,y,z) = \dfrac{6x^2e^{2y}}{z},$
$h_{yy}(x,y,z) = \dfrac{4x^3e^{2y}}{z},$
$h_{yz}(x,y,z) = −\dfrac{2x^3e^{2y}}{z^2},$
$h_{zx}(x,y,z) = −\dfrac{3x^2e^{2y}}{z^2},$
$h_{zy}(x,y,z) = −\dfrac{2x^3e^{2y}}{z^2},$
$h_{zz}(x,y,z) = \dfrac{2x^3e^{2y}}{z^3}$

Para los siguientes ejercicios, busque la ecuación del plano tangente a la superficie especificada en el punto dado.

15. $z=x^3−2y^2+y−1$en punto$(1,1,−1)$

16. $z=e^x+\dfrac{2}{y}$en punto$(0,1,3)$

Contestar: $z = x - 2y + 5$

17. Aproximado$f(x,y)=e^{x^2}+\sqrt{y}$ en$(0.1,9.1).$ Anota tu función de aproximación lineal$L(x,y).$ ¿Qué tan precisa es la aproximación a la respuesta exacta, redondeada a cuatro dígitos?

18. Encuentra el diferencial$dz$ de$h(x,y)=4x^2+2xy−3y$ y aproximado$Δz$ en el punto$(1,−2).$ Let$Δx=0.1$ y$Δy=0.01.$

Contestar: $dz=4\,dx−dy, \; dz(0.1,0.01)=0.39, \; Δz = 0.432$

19. Encuentra la derivada direccional de$f(x,y)=x^2+6xy−y^2$ en la dirección$\vecs v=\mathbf{\hat i}+4\,\mathbf{\hat j}.$

20. Encuentre la magnitud y dirección de la derivada direccional máxima para la función$f(x,y)=x^3+2xy−\cos(πy)$ en el punto$(3,0).$

Contestar: $3\sqrt{85}\langle 27, 6\rangle$

Para los siguientes ejercicios, encuentra el gradiente.

21. $c(x,t)=e(t−x)^2+3\cos t$

22. $f(x,y)=\dfrac{\sqrt{x}+y^2}{xy}$

Contestar: $\vecs \nabla f(x, y) = -\dfrac{\sqrt{x}+2y^2}{2x^2y}\,\mathbf{\hat i} + \left( \dfrac{1}{x} + \dfrac{1}{\sqrt{x}y^2} \right) \,\mathbf{\hat j}$

Para el siguiente ejercicio, encontrar y clasificar los puntos críticos.

23. $z=x^3−xy+y^2−1$

Para los siguientes ejercicios, use multiplicadores Lagrange para encontrar los valores máximo y mínimo para las funciones con las restricciones dadas.

24. $f(x,y)=x^2y,$sujeto a la restricción:$x^2+y^2=4$

Contestar: máximo:$\dfrac{16}{3\sqrt{3}},$ mínimo:$-\dfrac{16}{3\sqrt{3}},$

25. $f(x,y)=x^2−y^2,$sujeto a la restricción:$x+6y=4$

26. Un maquinista está construyendo un cono circular derecho a partir de un bloque de aluminio. La máquina da un error$5\%$ de altura y$2\%$ radio. Encuentra el error máximo en el volumen del cono si el maquinista crea un cono de altura$6$ cm y radio$2$ cm.

Contestar: $2.3228$cm ³

27. Un compactador de basura tiene la forma de un cuboide. Supongamos que el compactador de basura está lleno de líquido incompresible. La longitud y el ancho están disminuyendo a velocidades de$2$ pies/seg y$3$ pies/seg, respectivamente. Encuentre la velocidad a la que aumenta el nivel de líquido cuando la longitud es$14$ ft, el ancho es$10$ ft y la altura es$4$ ft.