15.2E: Ejercicios para la Sección 15.2

Última actualización
Guardar como PDF

Page ID: 116258

Edwin “Jed” Herman & Gilbert Strang
OpenStax

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1) La región$D$ delimitada por$y = x^3, \space y = x^3 + 1, \space x = 0,$ y$x = 1$ como se da en la siguiente figura.

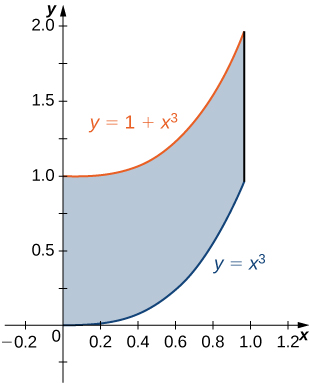
$Una región está delimitada por y = 1 + x en cubos, y = x en cubos, x = 0 y x = 1.$

a. Clasificar esta región como vertical simple (Tipo I) u horizontalmente simple (Tipo II).

Tipo:: Tipo I pero no Tipo II

b. Encontrar el área de la región$D$.

c. Find the average value of the function $f(x,y) = 3xy$ on the region graphed in the previous exercise.

Answer: $\frac{27}{20}$

2) The region $D$ bounded by $y = \sin x, \space y = 1 + \sin x, \space x = 0$, and $x = \frac{\pi}{2}$ as given in the following figure.

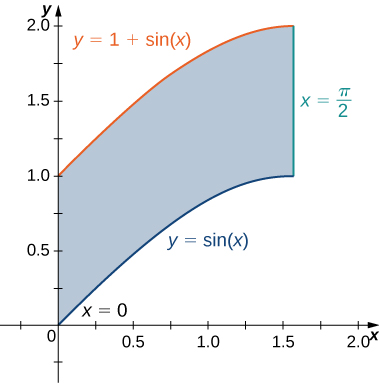
$A region is bounded by y = 1 + sin x, y = sin x, x = 0, and x = pi/2.$

a. Clasificar esta región como vertical simple (Tipo I) u horizontalmente simple (Tipo II).

Tipo:: Tipo I pero no Tipo II

b. Encontrar la zona de la región$D$.

Contestar: $\frac{\pi}{2}\, \text{units}^2$

c. Encuentra el valor promedio de la función$f(x,y) = \cos x$ en la región$D$.

3) La región$D$ delimitada por$x = y^2 - 1$ y$x = \sqrt{1 - y^2}$ como se da en la siguiente figura.

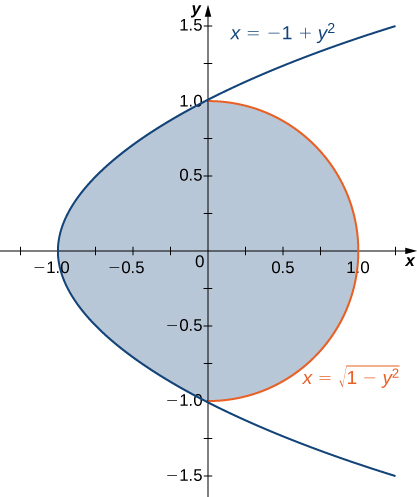
$Una región está delimitada por x = negativo 1 + y cuadrado y x = la raíz cuadrada de la cantidad (1 menos y al cuadrado).$

a. Clasificar esta región como vertical simple (Tipo I) u horizontalmente simple (Tipo II).

Tipo:: Tipo II pero no Tipo I

b. Encuentra el volumen del sólido bajo la gráfica de la función$f(x,y) = xy + 1$ and above the region $D$.

Answer: $\frac{1}{6}(8 + 3\pi)\, \text{units}^3$

4) The region $D$ bounded by $y = 0, \space x = -10 + y,$ and $x = 10 - y$ as given in the following figure.

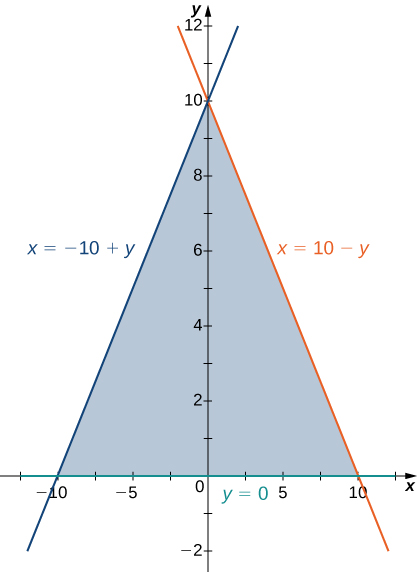
$A region is bounded by x = negative 10 + y, x = 10 minus y, and y = 0.$

a. Clasificar esta región como vertical simple (Tipo I) u horizontalmente simple (Tipo II).

Tipo:: Tipo II pero no Tipo I

b. encontrar el volumen del sólido bajo la gráfica de la función$f(x,y) = x + y$ y por encima de la región en la figura del ejercicio anterior.

Contestar: $\frac{1000}{3}\, \text{units}^3$

5) La región$D$ delimitada por$y = 0, \space x = y - 1, \space x = \frac{\pi}{2}$ como se indica en la siguiente figura.

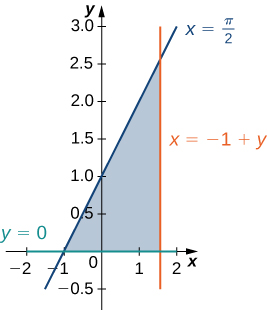
$Una región está delimitada por x = pi/2, y = 0, y x = negativo 1 + y.$

Clasificar esta región como vertical simple (Tipo I) u horizontalmente simple (Tipo II).

Tipo:: Tipo I y Tipo II

6) La región$D$ bounded by $y = 0$ and $y = x^2 - 1$ as given in the following figure.

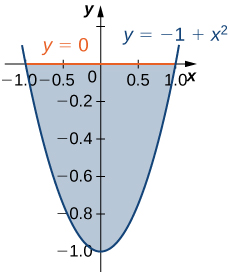
$A region is bounded by y = 0 and y = negative 1 + x squared.$

Clasificar esta región como vertical simple (Tipo I) u horizontalmente simple (Tipo II).

Tipo:: Tipo I y Tipo II

7) Dejar$D$ ser la región delimitada por las curvas de ecuaciones$y = \cos x$ y$y = 4 - x^2$ y el$x$ eje -eje. Explique por qué no$D$ es ni de Tipo I ni de II.

Contestar: La región no$D$ es de Tipo I: no se encuentra entre dos líneas verticales y las gráficas de dos funciones continuas$g_1(x)$ y$g_2(x)$. La región no es de Tipo II: no se encuentra entre dos líneas horizontales y las gráficas de dos funciones continuas$h_1(y)$ y$h_2(y)$.

8) Dejar$D$ ser la región delimitada por las curvas de ecuaciones$y = x, \space y = -x$ y$y = 2 - x^2$. Explique por qué no$D$ es ni de Tipo I ni de II.

En los ejercicios 9 - 14, evaluar la doble integral$\displaystyle \iint_D f(x,y) \,dA$ sobre la región$D$.

9)$f(x,y) = 1$ y

$D = \big\{(x,y)| \, 0 \leq x \leq \frac{\pi}{2}, \space \sin x \leq y \leq 1 + \sin x \big\}$

Contestar: $\frac{\pi}{2}$

10)$f(x,y) = 2$ y

$D = \big\{(x,y)| \, 0 \leq y \leq 1, \space y - 1 \leq x \leq \arccos y \big\}$

11)$f(x,y) = xy$ y

$D = \big\{(x,y)| \, -1 \leq y \leq 1, \space y^2 - 1 \leq x \leq \sqrt{1 - y^2} \big\}$

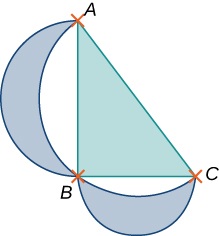
Contestar: $0$

12)$f(x,y) = \sin y$ y$D$ es la región triangular con vértices$(0,0), \space (0,3)$, y$(3,0)$

13)$f(x,y) = -x + 1$ y$D$ es la región triangular con vértices$(0,0), \space (0,2)$, y$(2,2)$

Contestar: $\frac{2}{3}$

14)$f(x,y) = 2x + 4y$ y

$D = \big\{(x,y)|\, 0 \leq x \leq 1, \space x^3 \leq y \leq x^3 + 1 \big\}$

En los ejercicios 15 - 20, evaluar las integrales iteradas.

15)$\displaystyle \int_0^1 \int_{2\sqrt{x}}^{2\sqrt{x}+1} (xy + 1) \,dy \space dx$

Contestar: $\frac{41}{20}$

16)$\displaystyle \int_0^3 \int_{2x}^{3x} (x + y^2) \,dy \space dx$

17)$\displaystyle \int_1^2 \int_{-u^2-1}^{-u} (8 uv) \,dv \space du$

Contestar: $-63$

18)$\displaystyle \int_e^{e^2} \int_{\ln u}^2 (v + \ln u) \,dv \space du$

19)$\displaystyle \int_0^{1/2} \int_{-\sqrt{1-4y^2}}^{\sqrt{1-4y^2}} 4 \,dx \space dy$

Contestar: $\pi$

20)$\displaystyle \int_0^1 \int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} (2x + 4y^3) \,dx \space dy$

21) Dejemos$D$ ser la región delimitada por$y = 1 - x^2, \space y = 4 - x^2$, y los ejes$x$ - y$y$ -ejes.

a. Demostrar que$\displaystyle \iint_D x\,dA = \int_0^1 \int_{1-x^2}^{4-x^2} x \space dy \space dx + \int_1^2 \int_0^{4-x^2} x \space dy \space dx$ dividiendo la región$D$ en dos regiones de Tipo I.

b. Evaluar la integral$\displaystyle \iint_D x \,dA.$

22) Dejar$D$ ser la región delimitada por$y = 1, \space y = x, \space y = \ln x$, y el$x$ -eje.

a. mostrar que$\displaystyle \iint_D y^2 \,dA = \int_{-1}^0 \int_{-x}^{2-x^2} y^2 dy \space dx + \int_0^1 \int_x^{2-x^2} y^2 dy \space dx$ dividiendo la región$D$ en dos regiones de Tipo I, donde$D = \big\{(x,y)\,|\,y \geq x, y \geq -x, \space y \leq 2-x^2\big\}$.

b. Evaluar la integral$\displaystyle \iint_D y^2 \,dA.$

23)$D$ Sea la región delimitada por$y = x^2$,$y = x + 2$, y$y = -x$.

a. Demostrar que$\displaystyle \iint_D x \, dA = \int_0^1 \int_{-y}^{\sqrt{y}} x \space dx \space dy + \int_1^4 \int_{y-2}^{\sqrt{y}} x \space dx \space dy$ dividiendo la región$D$ en dos regiones de Tipo II, donde$D = \big\{(x,y)\,|\,y \geq x^2, \space y \geq -x, \space y \leq x + 2\big\}$.

b. Evaluar la integral$\displaystyle \iint_D x \,dA.$

Contestar: a. Las respuestas pueden variar;
b.$\frac{8}{12}$

24) La región$D$ delimitada por$x = 0, y = x^5 + 1$, y$y = 3 - x^2$ se muestra en la siguiente figura. Encuentra la zona$A(D)$ de la región$D$.

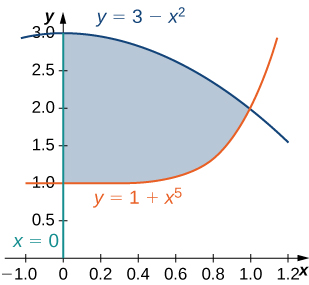
$Una región está delimitada por y = 1 + x a la quinta potencia, y = 3 menos x al cuadrado y x = 0.$

25) La región$D$ bounded by $y = \cos x, \space y = 4 + \cos x$, and $x = \pm \frac{\pi}{3}$ is shown in the following figure. Find the area $A(D)$ of the region $D$.

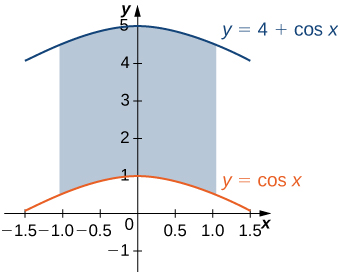
$A region is bounded by y = cos x, y = 4 + cos x, x = negative 1, and x = 1.$

Contestar: $\frac{8\pi}{3}$

26) Encontrar la zona$A(D)$ de la región$D = \big\{(x,y)| \, y \geq 1 - x^2, y \leq 4 - x^2, \space y \geq 0, \space x \geq 0 \big\}$.

27) Dejar$D$ ser la región delimitada por$ y = 1, \space y = x, \space y = \ln x$, y el$x$ -eje. Encuentra la zona$A(D)$ de la región$D$.

Contestar: $\left(e - \frac{3}{2}\right)\, \text{units}^2$

28) Encontrar el valor promedio de la función$f(x,y) = \sin y$ en la región triangular con vértices$(0,0), \space (0,3)$, y$(3,0)$.

29) Encontrar el valor promedio de la función$f(x,y) = -x + 1$ en la región triangular con vértices$(0,0), \space (0,2)$, y$(2,2)$.

Contestar: El valor promedio de$f$ en esta región triangular es$\frac{1}{3}.$

En los ejercicios 30 - 33, cambiar el orden de integración y evaluar la integral.

30)$\displaystyle \int_{-1}^{\pi/2} \int_0^{x+1} \sin x \, dy \, dx$

31)$\displaystyle \int_0^1 \int_{x-1}^{1-x} x \, dy \, dx$

Contestar: $\displaystyle \int_0^1 \int_{x-1}^{1-x} x \space dy \space dx = \int_{-1}^0 \int_0^{y+1} x \space dx \space dy + \int_0^1 \int_0^{1-y} x \space dx \space dy = \frac{1}{3}$

32)$\displaystyle \int_{-1}^0 \int_{-\sqrt{y+1}}^{\sqrt{y+1}} y^2 dx \space dy$

33)$\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy$

Contestar: $\displaystyle \int_{-1/2}^{1/2} \int_{-\sqrt{y^2+1}}^{\sqrt{y^2+1}} y \space dx \space dy = \int_1^2 \int_{-\sqrt{x^2-1}}^{\sqrt{x^2-1}} y \space dy \space dx = 0$

34) La región$D$ se muestra en la siguiente figura. Evaluar la doble integral$\displaystyle \iint_D (x^2 + y) \,dA$ utilizando el orden de integración más fácil.

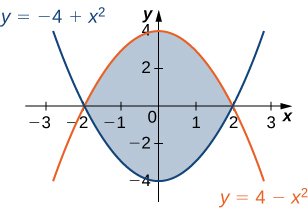
$Una región está delimitada por y = negativo 4 + x cuadrado e y = 4 menos x cuadrado.$

35) La región$D$ is shown in the following figure. Evaluate the double integral $\displaystyle \iint_D (x^2 - y^2) \,dA$ by using the easier order of integration.

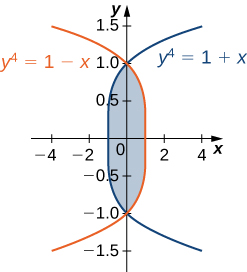
$A region is bounded by y to the fourth power = 1 minus x and y to the fourth power = 1 + x.$

Contestar: $\displaystyle \iint_D (x^2 - y^2) dA = \int_{-1}^1 \int_{y^4-1}^{1-y^4} (x^2 - y^2)dx \space dy = \frac{464}{4095}$

36) Encuentra el volumen del sólido bajo la superficie$z = 2x + y^2$ y por encima de la región delimitada por$y = x^5$ y$y = x$.

37) Encontrar el volumen del sólido bajo el plano$z = 3x + y$ y por encima de la región determinada por$y = x^7$ y$y = x$.

Contestar: $\frac{4}{5}\, \text{units}^3$

38) Encontrar el volumen del sólido bajo el plano$z = 3x + y$ y por encima de la región delimitada por$x = \tan y, \space x = -\tan y$, y$x = 1$.

39) Encuentra el volumen del sólido debajo de la superficie$z = x^3$ y por encima de la región plana delimitada por$x = \sin y, \space x = -\sin y$, y$x = 1$.

Contestar: $\frac{5\pi}{32}\, \text{units}^3$

40) Dejar$g$ ser una función positiva, creciente y diferenciable en el intervalo$[a,b]$. Mostrar que el volumen del sólido bajo la superficie$z = g'(x)$ y por encima de la región delimitada por$y = 0, \space y = g(x), \space x = a$, y$x = b$ está dada por$\frac{1}{2}(g^2 (b) - g^2 (a))$.

41) Dejar$g$ ser una función positiva, creciente y diferenciable en el intervalo$[a,b]$ y dejar$k$ ser un número real positivo. Mostrar que el volumen del sólido bajo la superficie$z = g'(x)$ y por encima de la región delimitada por$y = g(x), \space y = g(x) + k, \space x = a$, y$x = b$ está dado por$k(g(b) - g(a)).$

42) Encontrar el volumen del sólido situado en el primer octante y determinado por los planos$z = 2$,$z = 0, \space x + y = 1, \space x = 0$, y$y = 0$.

43) Encontrar el volumen del sólido situado en el primer octante y delimitado por los planos$x + 2y = 1$,$x = 0, \space z = 4$, y$z = 0$.

Contestar: $1\, \text{units}^3$

44) Encontrar el volumen del sólido delimitado por los planos$x + y = 1, \space x - y = 1, \space x = 0, \space z = 0$, y$z = 10$.

45) Encontrar el volumen del sólido delimitado por los planos$x + y = 1, \space x - y = 1, \space x + y = -1\space x - y = -1, \space z = 1$, y$z = 0$

Contestar: $2\, \text{units}^3$

46) Dejar$S_1$ y$S_2$ ser los sólidos situados en el primer octante bajo los planos$x + y + z = 1$ y$x + y + 2z = 1$ respectivamente, y dejar que$S$ sea el sólido situado entre$S_1, \space S_2, \space x = 0$, y$y = 0$.

Encuentra el volumen del sólido$S_1$.
Encuentra el volumen del sólido$S_2$.
Encontrar el volumen del sólido$S$ restando los volúmenes de los sólidos$S_1$ y$S_2$.

47) Dejar$S_1$ y$S_2$ ser los sólidos situados en el primer octante bajo los planos$2x + 2y + z = 2$ y$x + y + z = 1$ respectivamente, y dejar que$S$ sea el sólido situado entre$S_1, \space S_2, \space x = 0$, y$y = 0$.

Encuentra el volumen del sólido$S_1$.
Encuentra el volumen del sólido$S_2$.
Encontrar el volumen del sólido$S$ restando los volúmenes de los sólidos$S_1$ y$S_2$.

Contestar: a.$\frac{1}{3}\, \text{units}^3$
b.$\frac{1}{6}\, \text{units}^3$
c.$\frac{1}{6}\, \text{units}^3$

48) Dejar$S_1$ y$S_2$ ser los sólidos situados en el primer octante bajo el plano$x + y + z = 2$ y debajo de la esfera$x^2 + y^2 + z^2 = 4$, respectivamente. Si el volumen del sólido$S_2$ es$\frac{4\pi}{3}$ determinar el volumen del sólido$S$ situado entre$S_1$ y$S_2$ restando los volúmenes de estos sólidos.

49) Dejar$S_1$ y$S_2$ ser los sólidos situados en el primer octante bajo el plano$x + y + z = 2$ y delimitados por el cilindro$x^2 + y^2 = 4$, respectivamente.

Encuentra el volumen del sólido$S_1$.
Encuentra el volumen del sólido$S_2$.
Encontrar el volumen del sólido$S$ situado entre$S_1$ y$S_2$ restando los volúmenes de los sólidos$S_1$ y$S_2$.

Contestar: a.$\frac{4}{3}\, \text{units}^3$
b.$2\pi\, \text{units}^3$
c.$\frac{6\pi - 4}{3}\, \text{units}^3$

50) [T] La siguiente figura muestra la región$D$ delimitada por las curvas$y = \sin x, \space x = 0$, y$y = x^4$. Utilice una calculadora gráfica o CAS para encontrar las$x$ coordenadas de los puntos de intersección de las curvas y determinar el área de la región$D$. Redondee sus respuestas a seis decimales.

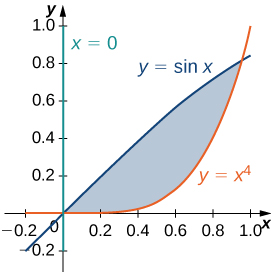
$Una región está limitada por y = sin x, y = x a la cuarta potencia, y x = 0.$

51) [T] La región$D$ bounded by the curves $y = \cos x, \space x = 0$, and $y = x^3$ is shown in the following figure. Use a graphing calculator or CAS to find the $x$-coordinates of the intersection points of the curves and to determine the area of the region $D$. Round your answers to six decimal places.

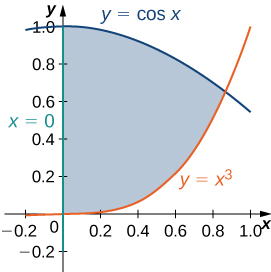
$A region is bounded by y = cos x, y = x cubed, and x = 0.$

Contestar: 0 y 0.865474;$A(D) = 0.621135\, \text{units}^3$

52) Supongamos que ese$(X,Y)$ es el resultado de un experimento que debe ocurrir en una región determinada$S$ en el$xy$ plano. En este contexto, la región$S$ se denomina espacio muestral del experimento y$X$ y$Y$ son variables aleatorias. Si$D$ es una región incluida en$S$, entonces la probabilidad de$(X,Y)$ estar en$D$ se define como$P[(X,Y) \in D] = \iint_D p(x,y)dx \space dy$, donde$p(x,y)$ está la densidad de probabilidad conjunta del experimento. Aquí,$p(x,y)$ es una función no negativa para la cual$\iint_S p(x,y) dx \space dy = 1$. Supongamos que un punto$(X,Y)$ se elige arbitrariamente en el cuadrado$[0,3] \times [0,3]$ con la densidad de probabilidad

\[p(x,y) = \frac{1}{9} (x,y) \in [0,3] \times [0,3],\nonumber \]

\[p(x,y) = 0 \space \text{otherwise}\nonumber \]

Encuentra la probabilidad de que el punto$(X,Y)$ esté dentro del cuadrado unitario e interpreta el resultado.

53) Considerar$X$ y$Y$ dos variables aleatorias de densidades de probabilidad$p_1(x)$ y$p_2(x)$, respectivamente. Las variables aleatorias$X$ y$Y$ se dice que son independientes si su función de densidad conjunta viene dada por$p_(x,y) = p_1(x)p_2(y)$. En un restaurante drive-thru, los clientes pasan, en promedio, 3 minutos haciendo sus pedidos y 5 minutos adicionales pagando y recogiendo sus comidas. Supongamos que realizar el pedido y pagar/recoger la comida son dos eventos independientes$X$ y$Y$. Si los tiempos de espera son modelados por las densidades de probabilidad exponencial

\[p_1(x) = \frac{1}{3}e^{-x/3} \space x\geq 0,\nonumber \]

\[p_1(x) = 0 \space \text{otherwise}\nonumber \]

\[p_2(y) = \frac{1}{5} e^{-y/5} \space y \geq 0\nonumber \]

\[p_2(y) = 0 \space \text{otherwise}\nonumber \]

respectivamente, la probabilidad de que un cliente pase menos de 6 minutos en la línea drive-thru viene dada por$P[X + Y \leq 6] = \iint_D p(x,y) dx \space dy$, donde$D = {(x,y)|x \geq 0, \space y \geq 0, \space x + y \leq 6}$. Encuentra$P[X + Y \leq 6]$ e interpreta el resultado.

Contestar: $P[X + Y \leq 6] = 1 + \frac{3}{2e^2} - \frac{5}{e^{6/5}} \approx 0.45$; existe la$45\%$ posibilidad de que un cliente pase$6$ minutos en la línea drive-thru.

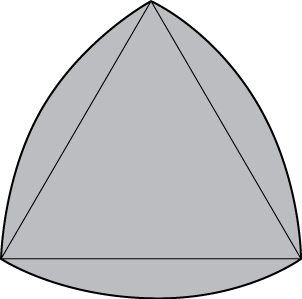
54) [T] El triángulo de Reuleaux consiste en un triángulo equilátero y tres regiones, cada una de ellas delimitada por un lado del triángulo y un arco de un círculo de radio s centrado en el vértice opuesto del triángulo. Mostrar que el área del triángulo de Reuleaux en la siguiente figura de longitud lateral$s$ es$\frac{s^2}{2}(\pi - \sqrt{3})$.

$Un triángulo equilátero con regiones adicionales que consta de tres arcos de un círculo con radio igual a la longitud del lado del triángulo. Estos arcos conectan dos vértices adyacentes, y el radio se toma del vértice opuesto.$

55) [T] Demostrar que la zona del lunes de Alhazen, los dos lunes azules en la siguiente figura, es la misma que la zona del triángulo rectángulo$ABC.$ The outer boundaries of the lunes are semicircles of diameters $AB$ and $AC$ respectively, and the inner boundaries are formed by the circumcircle of the triangle $ABC$.

$A right triangle with points A, B, and C. Point B has the right angle. There are two lunes drawn from A to B and from B to C with outer diameters AB and AC, respectively, and with the inner boundaries formed by the circumcircle of the triangle ABC.$