15.5: Integrales triples en coordenadas cilíndricas y esféricas
- Page ID
- 116290
- Evaluar una triple integral cambiando a coordenadas cilíndricas.
- Evaluar una triple integral cambiando a coordenadas esféricas.
Anteriormente en este capítulo mostramos cómo convertir una doble integral en coordenadas rectangulares en una doble integral en coordenadas polares para tratar de manera más conveniente los problemas que involucran la simetría circular. Una situación similar ocurre con las integrales triples, pero aquí necesitamos distinguir entre simetría cilíndrica y simetría esférica. En esta sección convertimos integrales triples en coordenadas rectangulares en una triple integral en coordenadas cilíndricas o esféricas.
Recordemos también el preludio capitular, que mostraba el teatro de ópera L'hemisphèric en Valencia, España. Tiene cuatro secciones siendo una de las secciones un teatro en una esfera (pelota) de cinco pisos de altura bajo un techo ovalado tan larga como un campo de fútbol. En su interior hay una pantalla IMAX que transforma la esfera en un planetario con un cielo lleno de estrellas\(9000\) centelleantes. Utilizando integrales triples en coordenadas esféricas, podemos encontrar los volúmenes de diferentes formas geométricas como estas.
Revisión de coordenadas cilíndricas
Como hemos visto anteriormente, en el espacio bidimensional se\((x,y)\) puede identificar\(\mathbb{R}^2\) un punto con coordenadas rectangulares con\((r,\theta)\) en coordenadas polares y viceversa, donde\(x = r \, \cos \theta\),\(y = r \, \sin \, \theta, \, r^2 = x^2 + y^2\) y\(\tan \, \theta = \left(\frac{y}{x}\right)\) son las relaciones entre las variables.
En el espacio tridimensional se\((x,y,z)\) puede identificar\(\mathbb{R}^3\) un punto con coordenadas rectangulares con coordenadas cilíndricas\((r, \theta, z)\) y viceversa. Podemos usar estas mismas relaciones de conversión, agregando\(z\) como la distancia vertical al punto desde el\((xy\) plano -como se muestra en\(\PageIndex{1}\).
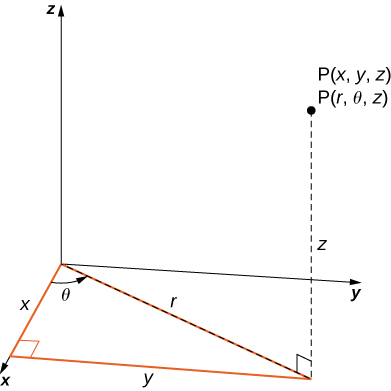
Para convertir de coordenadas rectangulares a cilíndricas, utilizamos la conversión
- \(x = r \, \cos \theta\)
- \(y = r \, \sin \, \theta\)
- \(z=z\)
Para convertir de coordenadas cilíndricas a rectangulares, utilizamos
- \(r^2 = x^2 + y^2\)y
- \(\theta = \tan^{-1} \left(\frac{y}{x}\right)\)
- \(z=z\)
Tenga en cuenta que esa\(z\) coordenada sigue siendo la misma en ambos casos.
En el plano bidimensional con un sistema de coordenadas rectangular, cuando decimos\(x = k\) (constante) nos referimos a una línea vertical no acotada paralela al\(y\) eje -y cuando\(y = l\) (constante) nos referimos a una línea horizontal no acotada paralela al\(x\) eje -eje. Con el sistema de coordenadas polares, cuando decimos\(r = c\) (constante), nos referimos a un círculo de\(c\) unidades de radio y cuando\(\theta = \alpha\) (constante) nos referimos a un rayo infinito haciendo un ángulo\(\alpha\) con el\(x\) eje positivo.
De igual manera, en\((x,y,z)\) el espacio tridimensional con coordenadas rectangulares las ecuaciones\(x = k, \, y = l\)\(k, \, l\) y\(z = m\) donde y\(m\) son constantes, representan planos no delimitados paralelos al\(yz\) -plano,\(xz\) -plano y\(xy\) -plano, respectivamente. Con coordenadas cilíndricas\((r, \theta, z)\)\(r = c, \, \theta = \alpha\), por\(z = m\), y, donde\(c, \alpha\), y\(m\) son constantes, nos referimos a un cilindro vertical sin límites con el eje z como eje radial; un plano que forma un ángulo constante\(\alpha\) con el\(xy\) plano -y un plano horizontal no acotado paralelo al\(xy\) plano -respectivamente. Esto significa que el cilindro circular\(x^2 + y^2 = c^2\) en coordenadas rectangulares se puede representar simplemente como\(r = c\) en coordenadas cilíndricas. (Consulte Coordenadas Cilíndricas y Esféricas para más revisión.)
Integración en coordenadas cilíndricas
Las integrales triples a menudo se pueden evaluar más fácilmente usando coordenadas cilíndricas en lugar de coordenadas rectangulares. Algunas ecuaciones comunes de superficies en coordenadas rectangulares junto con ecuaciones correspondientes en coordenadas cilíndricas se enumeran en la Tabla\(\PageIndex{1}\). Estas ecuaciones serán útiles a medida que avanzamos con la resolución de problemas usando integrales triples.
| Cilindro circular | Cono circular | Esfera | Paraboloide | |
|---|---|---|---|---|
| Rectangular | \(x^2 + y^2 = c^2\) | \(z^2 = c^2 (x^2 + y^2)\) | \(x^2 + y^2 + z^2 = c^2\) | \(z = c(x^2 + y^2)\) |
| Cilindrica | \(r = c\) | \(z = cr\) | \(r^2 + z^2 = c^2\) | \(z = cr^2\) |
Como antes, comenzamos con la región\(B\) delimitada más simple\(\mathbb{R}^3\) para describirla en coordenadas cilíndricas, en forma de caja cilíndrica,\(B = \{(r,\theta,z) | a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}\) (Figura\(\PageIndex{2}\)). Supongamos que dividimos cada intervalo en\(l, \, m\), y\(n\) subdivisiones tales que\(\Delta r = \frac{b \cdot a}{l}, \, \Delta \theta = \frac{\beta \cdot \alpha}{m}\), y\(\Delta z = \frac{d \cdot c}{n}\). Entonces podemos exponer la siguiente definición para una triple integral en coordenadas cilíndricas.
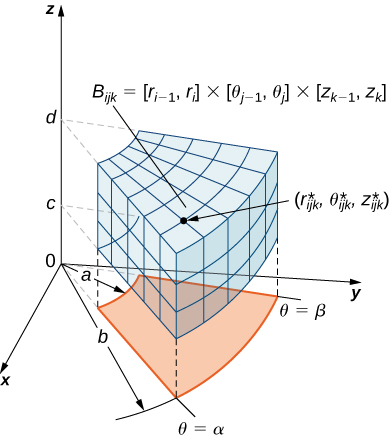
Considere la caja cilíndrica (expresada en coordenadas cilíndricas)
\[B = \{(r, \theta, z)|a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}. \nonumber \]
Si la función\(f(r, \theta, z)\) es continua\(B\) y si\((r_{ijk}^*, \theta_{ijk}^*, z_{ijk}^*)\) hay algún punto de muestra en el subcuadro cilíndrico\(B_{ijk} = |r_{i-1}, r_i| \times |\theta_{j-1}, \theta_j| \times |z_{k-1}, k_i|\) (Figura\(\PageIndex{2}\)), entonces podemos definir la triple integral en coordenadas cilíndricas como el límite de una suma triple de Riemann, siempre que exista el siguiente límite:
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(r_{ijk}^*, \theta_{ijk}^*, z_{ijk}^*) \Delta r \Delta \theta \Delta z. \nonumber \]
Tenga en cuenta que si\(g(x,y,z)\) es la función en coordenadas rectangulares y la caja\(B\) se expresa en coordenadas rectangulares, entonces la triple integral
\[\iiint_B g(x,y,z)dV \nonumber \]
es igual a la triple integral
\[\iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz \nonumber \]
y tenemos
\[\iiint_B g(x,y,z)dV = \iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz = \iiint_B f(r, \theta \, z) r \, dr \, d\theta \, dz. \nonumber \]
Como se mencionó en el apartado anterior, todas las propiedades de una doble integral funcionan bien en triples integrales, ya sea en coordenadas rectangulares o en coordenadas cilíndricas. También se mantienen para integrales iteradas. Para reiterar, en coordenadas cilíndricas, el teorema de Fubini toma la siguiente forma:
Supongamos que\(g(x,y,z)\) es continuo sobre una caja rectangular\(B\) que cuando se describe en coordenadas cilíndricas se ve así\(B = \{(r,\theta,z) | a \leq r \leq b, \, \alpha \leq \theta \leq \beta, \, c \leq z \leq d\}\).
Entonces\(g(x,y,z) = g(r \, \cos \theta, r \, \sin \, \theta,z) = f(r, \theta,z)\) y
\[\iiint_B g(x,y,z)dV = \int_c^d \int_{\beta}^{\alpha} \int_a^b f(r, \theta, z) r \, dr \, d\theta \, dz. \nonumber \]
La integral iterada puede ser reemplazada de manera equivalente por cualquiera de las otras cinco integrales iteradas obtenidas integrando con respecto a las tres variables en otros órdenes.
Los sistemas de coordenadas cilíndricos funcionan bien para sólidos que son simétricos alrededor de un eje, como cilindros y conos. Veamos algunos ejemplos antes de definir la triple integral en coordenadas cilíndricas en regiones cilíndricas generales.
Evaluar la triple integral
\[\iiint_B (zr \, \sin \, \theta) r \, dr \, d\theta \, dz \nonumber \]
donde se\(B\) encuentra la caja cilíndrica\(B = \{(r,\theta,z) |0 \leq r \leq 2, \, 0 \leq \theta \leq \pi/2, \, 0, \leq z \leq 4\}.\)
Solución
Como se afirma en el teorema de Fubini, podemos escribir la triple integral como la integral iterada
\[\iiint_B (zr \, \sin \, \theta) r \, dr \, d\theta \, dz = \int_{\theta=0}^{\theta=\pi/2} \int_{r=0}^{r=2} \int_{z=0}^{z=4} (zr \, \sin \, \theta) r \, dz \, dr \, d\theta. \nonumber \]
La evaluación de la integral iterada es sencilla. Cada variable en la integral es independiente de las demás, por lo que podemos integrar cada variable por separado y multiplicar los resultados juntos. Esto hace que el cálculo sea mucho más fácil:
\[\int_{\theta=0}^{\theta=\pi/2} \int_{r=0}^{r=2} \int_{z=0}^{z=4} (zr \, \sin \, \theta) r \, dz \, dr \, d\theta = \left(\int_0^{\pi/2} \sin \, \theta \, d\theta \right) \left( \int_0^2 r^2 dr\right) \left( \int_0^4 z \, dz\right) = \left(\left. -\cos \theta \right|_0^{\pi/2} \right) \left(\left.\frac{r^3}{3} \right|_0^2 \right) \left( \left. \frac{z^2}{2} \right|_0^4 \right) = \frac{64}{3}. \nonumber \]
Evaluar la triple integral\[\int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=1} \int_{z=0}^{z=4} rz \, \sin \, \theta r \, dz \, dr \, d\theta. \nonumber \]
- Pista
-
Sigue los mismos pasos que en el ejemplo anterior.
- Contestar
-
\(8\)
Si la región cilíndrica sobre la que tenemos que integrar es un sólido general, observamos las proyecciones sobre los planos de coordenadas. De ahí que la triple integral de una función continua\(f(r, \theta, z)\) sobre una región sólida general\(E = \{(r, \theta, z)|(r, \theta) \in D, u_1 (r, \theta) \leq z \leq u_2 (r, \theta)\}\) en\(\mathbb{R}^3\) donde\(D\) está la proyección de\(E\) sobre el\(r\theta\) plano, es
\[\iiint_E f(r, \theta, z) r \, dr \, d\theta \, dz = \iint_D \left[\int_{u_1(r,\theta)}^{u_2(r,\theta)} f(r, \theta, z) dz \right] r \, dr \, d\theta. \nonumber \]
En particular, si\(D = \{(r, \theta) |G_1 (\theta) \leq r \leq g_2(\theta), \alpha \leq \theta \leq \beta \}\), entonces tenemos
\[ \iiint_E f(r,\theta, z) r \, dr \, d\theta = \int_{\theta=\alpha}^{\theta=\beta} \int_{r=g_1(\theta)}^{r=g_2(\theta)} \int_{z=u_1(r,\theta)}^{z=u_2(r,\theta)} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
Existen fórmulas similares para proyecciones en los otros planos de coordenadas. Podemos usar coordenadas polares en esos planos si es necesario.
Considera la región\(E\) dentro del cilindro circular derecho con ecuación\(r = 2 \, \sin \, \theta\), delimitada abajo por el\(r\theta\) plano y delimitada arriba por la esfera con radio\(4\) centrado en el origen (Figura 15.5.3). Configure una triple integral sobre esta región con una función\(f(r, \theta, z)\) en coordenadas cilíndricas.
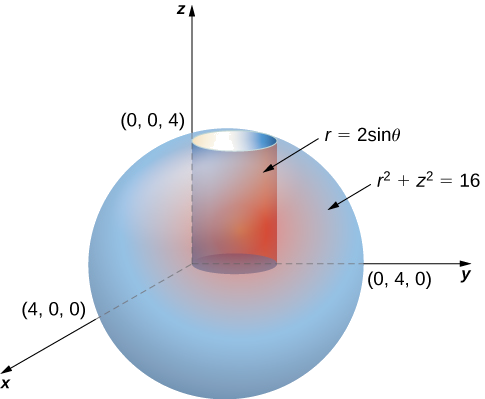
Solución
Primero, identificar que la ecuación para la esfera es\(r^2 + z^2 = 16\). Podemos ver que los límites para\(z\) son de\(0\) a\(z = \sqrt{16 - r^2}\). Entonces los límites para\(r\) son de\(0\) a\(r = 2 \, \sin \, \theta\). Por último, los límites para\(\theta\) son de\(0\) a\(\pi\). De ahí que la región sea\(E = \{(r,\theta, z)|0 \leq \theta \leq \pi, \, 0 \leq r \leq 2 \, \sin \, \theta, \, 0 \leq z \leq \sqrt{16 - r^2} \}.\) Por lo tanto, la triple integral es
\[\iiint_E f(r,\theta, z) r \, dz \, dr \, d\theta = \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \sin \, \theta} \int_{z=0}^{z=\sqrt{16-r^2}} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
Considera la región dentro del cilindro circular derecho con ecuación\(r=2 \, \sin \, \theta\) delimitada por debajo por el\(r\theta\) plano y delimitada arriba por\(z = 4 - y\). Configure una triple integral con una función\(f(r,\theta,z)\) en coordenadas cilíndricas.
- Pista
-
Analiza la región y dibuja un boceto.
- Contestar
-
\[\iiint_E f(r,\theta, z) r \, dz \, dr \, d\theta = \int_{\theta=0}^{\theta=\pi} \int_{r=0}^{r=2 \, \sin \, \theta} \int_{z=0}^{z=4-r \, \sin \, \theta} f(r,\theta,z) r \, dz \, dr \, d\theta. \nonumber \]
Dejar\(E\) ser la región delimitada abajo por el cono\(z = \sqrt{x^2 + y^2}\) y arriba por el paraboloide\(z = 2 - x^2 - y^2\). (Figura 15.5.4). Configure una triple integral en coordenadas cilíndricas para encontrar el volumen de la región, utilizando los siguientes órdenes de integración:
a.\(dz \, dr \, d\theta\)
b.\(dr \, dz \, d\theta\)
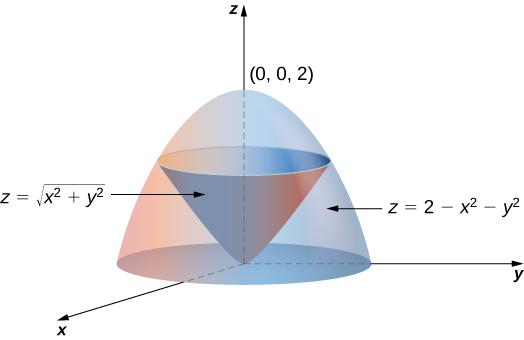
Solución
a. El cono es de radio 1 donde se encuentra con el paraboloide. Desde\(z = 2 - x^2 - y^2 = 2 - r^2\) y\(z = \sqrt{x^2 + y^2} = r^2\) (asumiendo que no\(r\) es negativo), tenemos\(2 - r^2 = r\). Resolviendo, tenemos\(r^2 + r - 2 = (r + 2)(r - 1) = 0\). Ya que\(r \geq 0\), tenemos\(r = 1\). Por lo tanto\(z = 1\). Entonces la intersección de estas dos superficies es un círculo de radio\(1\) en el plano\(z = 1\). El cono es el límite inferior para\(z\) y el paraboloide es el límite superior. La proyección de la región sobre el\(xy\) plano es el círculo de radio\(1\) centrado en el origen.
Así, podemos describir la región como\(E = \{(r, \theta, z) |0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 1, \, r \leq z \leq 2 - r^2 \}\).
De ahí que la integral para el volumen es
\[V = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \int_{z=r}^{z=2-r^2} r \, dz \, dr \, d\theta. \nonumber \]
b. también podemos escribir la superficie del cono como\(r = z\) y el paraboloide como\(r^2 = 2 - z\). El límite inferior para\(r\) es cero, pero el límite superior es a veces el cono y las otras veces es el paraboloide. El plano\(z = 1\) divide la región en dos regiones. Entonces la región puede describirse como\[E = \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 0 \leq z \leq 1, \, 0 \leq r \leq z\} \cup \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 1 \leq z \leq 2, \, 0 \leq r \leq \sqrt{2 - z}\}. \nonumber \]
Ahora la integral para el volumen se convierte
\[V = \int_{\theta=0}^{\theta=2\pi} \int_{z=0}^{z=1} \int_{r=0}^{r=z} r \, dr \, dz \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{z=1}^{z=2} \int_{r=0}^{r=\sqrt{2-z}} r \, dr \, dz \, d\theta. \nonumber \]
Rehacer el ejemplo anterior con el orden de integración\(d\theta \, dz \, dr\).
- Pista
-
Tenga en cuenta que\(\theta\) es independiente de\(r\) y\(z\).
- Contestar
-
\(E = \{(r,\theta,z)|0 \leq \theta \leq 2\pi, \, 0 \leq z \leq 1, \, 0 \leq r \leq 2 - z^2\}\)y\[V = \int_{r=0}^{r=1} \int_{z=0}^{z=2 - r^2} \int_{\theta=0}^{\theta=2\pi} r \, d\theta \, dz \, dr. \nonumber \]
Solución
a. Obsérvese que la ecuación para la esfera es
\[x^2 + y^2 + z^2 = 4 \, \text{or} \, r^2 + z^2 = 4 \nonumber \]
y la ecuación para el cilindro es
\[x^2 + y^2 = 1 \, \text{or} \, r^2 = 1. \nonumber \]
Así, tenemos para la región\(E\)
\[E = \{(r,\theta,z)|0 \leq z \leq \sqrt{4 - r^2}, \, 0 \leq r \leq 1, \, 0 \leq \theta \leq 2\pi\} \nonumber \]
De ahí que la integral para el volumen es
\[\begin{align} V (E) = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \int_{z=0}^{z=\sqrt{4-r^2}} r \, dz \, dr \, d\theta \\ = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \left[ \left>rz\right|_{z=0}^{z=\sqrt{4-r^2}}\right] dr \, d\theta = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=1} \left(r\sqrt{4 - r^2}\right) dr \, d\theta\\ = \int_0^{2\pi} \left(\frac{8}{3} - \sqrt{3} \right) d\theta = 2\pi \left(\frac{8}{3} - \sqrt{3} \right) \, \text{cubic units.} \end{align} \nonumber \]
b. ya que la esfera es\(x^2 + y^2 + z^2 = 4\), que es\(r^2 + z^2 = 4\), y el cilindro es\(x^2 + y^2 = 1\), que es\(r^2 = 1\), tenemos\(1 + z^2 = 4\), es decir,\(z^2 = 3\). Así tenemos dos regiones, ya que la esfera y el cilindro se cruzan\((1,\sqrt{3})\) en el\(rz\) plano -
\[E_1 = \{ (r,\theta,z) | 0 \leq r \leq \sqrt{4 - r^2}, \, \sqrt{3} \leq z \leq 2, \, 0 \leq \theta \leq 2\pi\} \nonumber \]y
\[E_2 = \{(r,\theta,z) | 0 \leq r \leq 1, \, 0 \leq z \leq \sqrt{3}, \, 0 \leq \theta \leq 2\pi\}. \nonumber \]
De ahí que la integral para el volumen es
\[\begin{align} V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{z=\sqrt{3}}^{z=2} \int_{r=0}^{r=\sqrt{4-r^2}} r \, dr \, dz \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{z=0}^{z=\sqrt{3}} \int_{r=0}^{r=1} r \, dr \, dz \, d\theta\\ = \sqrt{3} \pi + \left( \dfrac{16}{3} - 3 \sqrt{3} \right) \pi = 2\pi \left( \frac{8}{3} - \sqrt{3} \right) \, \text{cubic units.} \end{align} \nonumber \]
Rehacer el ejemplo anterior con el orden de integración\(d\theta \, dz \, dr\).
- Pista
-
Una figura puede ser útil. Tenga en cuenta que\(\theta\) es independiente de\(r\) y\(z\).
- Contestar
-
\(E_2 = \{(r,\theta,z) | 0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 1, \, r \leq z \leq \sqrt{4 - r^2}\}\)y
\[V = \int_{r=0}^{r=1} \int_{z=r}^{z=\sqrt{4-r^2}} \int_{\theta=0}^{\theta=2\pi} r \, d\theta \, dz \, dr. \nonumber \]
Revisión de Coordenadas Esféricas
En el espacio tridimensional\(\mathbb{R}^3\) en el sistema de coordenadas esféricas, especificamos un punto\(P\) por su distancia\(\rho\) desde el origen, el ángulo polar\(\theta\) desde el\(x\) eje positivo (igual que en el sistema de coordenadas cilíndrico), y el ángulo\(\varphi\) desde el positivo \(z\)-eje y la línea\(OP\) (Figura\(\PageIndex{6}\)). Tenga en cuenta que\(\rho > 0\) y\(0 \leq \varphi \leq \pi\). (Consulte Coordenadas Cilíndricas y Esféricas para una revisión.) Las coordenadas esféricas son útiles para integrales triples sobre regiones que son simétricas con respecto al origen.
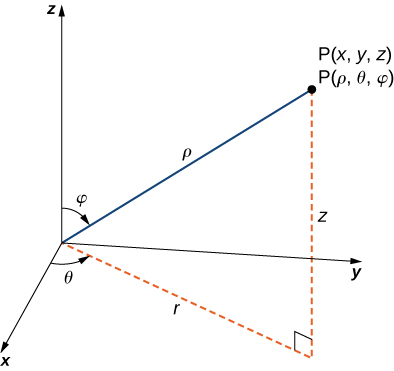
Recordemos las relaciones que conectan coordenadas rectangulares con coordenadas esféricas.
De coordenadas esféricas a coordenadas rectangulares:
\[x = \rho \, \sin \, \varphi \, \cos \theta, \, y = \rho \, \sin \, \varphi \, \sin \, \theta, \, and \, z = \rho \, \cos \, \varphi. \nonumber \]
De coordenadas rectangulares a coordenadas esféricas:
\[\rho^2 = x^2 + y^2 + z^2, \, \tan \, \theta = \frac{y}{x}, \, \varphi = \arccos \left( \frac{z}{\sqrt{x^2 + y^2 + z^2}}\right). \nonumber \]
Otras relaciones que es importante conocer para las conversiones son
- \(r = \rho \, \sin \, \varphi\)
- \(\theta = \theta\)Estas ecuaciones se utilizan para convertir de coordenadas esféricas a coordenadas cilíndricas.
- \(z = \rho \, \cos \, \varphi\)
y
- \(\rho = \sqrt{r^2 + z^2}\)
- \(\theta = \theta\)Estas ecuaciones se utilizan para convertir de coordenadas cilíndricas a coordenadas esféricas.
- \(\varphi = \arccos \left(\frac{z}{\sqrt{r^2 + z^2}}\right)\)
\(\PageIndex{7}\)muestra algunas regiones sólidas que son convenientes para expresar en coordenadas esféricas.
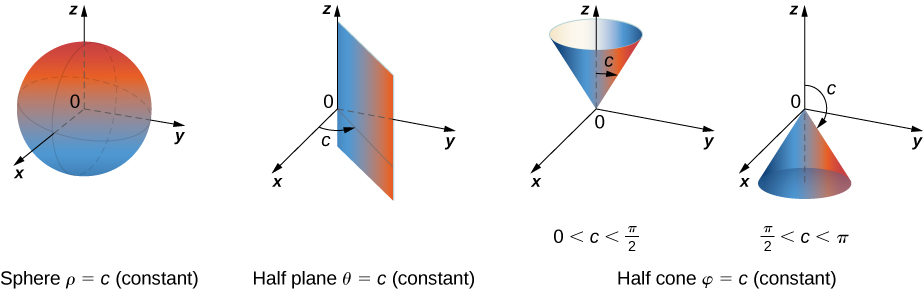
Integración en Coordenadas Esféricas
Ahora establecemos una triple integral en el sistema de coordenadas esféricas, como hicimos antes en el sistema de coordenadas cilíndricas. Deje que la función\(f(\rho,\theta,\varphi)\) sea continua en una caja esférica acotada,\(B = \{(\rho,\theta,\varphi) | a \leq \rho \leq b, \, \alpha \leq \theta \leq \beta, \, \gamma \leq \varphi \leq \psi \}\). Luego dividimos cada intervalo en\(l,m,n\) y\(n\) subdivisiones de tal manera que\(\Delta \rho = \frac{b - a}{l}, \, \Delta \theta = \frac{\beta - \alpha}{m}. \, \Delta \varphi = \frac{\psi - \gamma}{n}\). Ahora podemos ilustrar el siguiente teorema para integrales triples en coordenadas esféricas con\((\rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*)\) ser cualquier punto de muestra en el subcuadro esférico\(B_{ijk}\). Para el elemento volumen del subcuadro\(\Delta V\) en coordenadas esféricas, tenemos\(\Delta V = (\Delta \rho)\, (\rho \Delta \varphi)\, (\rho \, \sin \, \varphi \, \Delta \theta)\), como se muestra en la siguiente figura.
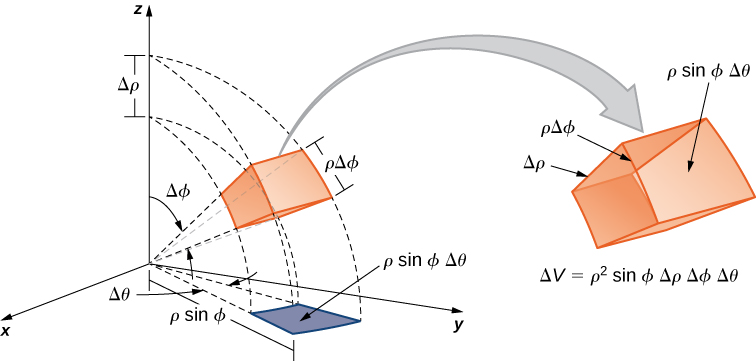
La triple integral en coordenadas esféricas es el límite de una triple suma de Riemann,
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( \rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*) (\rho_{ijk}^*)^2 \sin \, \varphi \Delta \rho \Delta \theta \Delta \varphi \nonumber \]
siempre que exista el límite.
Al igual que con las otras integrales múltiples que hemos examinado, todas las propiedades funcionan de manera similar para una triple integral en el sistema de coordenadas esféricas, y también lo hacen las integrales iteradas. El teorema de Fubini toma la siguiente forma.
Si\(f(\rho,\theta, \varphi)\) es continuo en una caja sólida esférica\(B = [a,b] \times [\alpha,\beta] \times [\gamma , \psi]\), entonces
\[\iiint_B f(\rho,\theta,\varphi ) \, \rho^2 \sin \, \varphi d\rho \, d\varphi \, d\theta = \int_{\varphi=\gamma}^{\varphi=\psi} \int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=a}^{\rho=b} f(\rho,\theta,\varphi) \, \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Esta integral iterada puede ser reemplazada por otras integrales iteradas integrando con respecto a las tres variables en otros órdenes.
Como se indicó anteriormente, los sistemas de coordenadas esféricas funcionan bien para sólidos que son simétricos alrededor de un punto, como esferas y conos. Veamos algunos ejemplos antes de considerar integrales triples en coordenadas esféricas en regiones esféricas generales.
Evaluar la triple integral iterada
\[\int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/2} \int_{\rho=0}^{\rho=1} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Solución
Como antes, en este caso las variables en la integral iterada son realmente independientes entre sí y de ahí podemos integrar cada pieza y multiplicar:
\[\int_0^{2\pi} \int_0^{\pi/2} \int_0^1 \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta = \int_0^{2\pi} d\theta \int_0^{\pi/2} \sin \, \varphi \, d\varphi \int_0^1 \rho^2 d\rho = (2\pi) \, (1) \, \left(\frac{1}{3}\right) = \frac{2\pi}{3} \nonumber \]
El concepto de triple integración en coordenadas esféricas se puede extender a la integración sobre un sólido general, utilizando las proyecciones en los planos de coordenadas. Tenga en cuenta que\(dV\) y\(dA\) media los incrementos en volumen y área, respectivamente. Las variables\(V\) y se\(A\) utilizan como variables de integración para expresar las integrales.
La triple integral de una función continua\(f(\rho,\theta,\varphi)\) sobre una región sólida general
\[E = \{(\rho,\theta,\varphi) |(\rho,\theta) \in D, u_1 (\rho, \theta) \leq \varphi \leq u_2 (\rho,\theta)\} \nonumber \]
en\(\mathbb{R}^3\), donde\(D\) esta la proyeccion de\(E\) sobre el\(\rho \theta\) -plano, es
\[\iiint_E f(\rho, \theta,\varphi) dV = \iint_D \left[ \int_{u_1(\rho,\theta)}^{u_2(\rho,\theta)} f(\rho,\theta,\varphi) \, d\varphi \right] \, dA. \nonumber \]
En particular\(D = \{(\rho,\theta) | g_1 (\theta) \leq \rho \leq g_2 (\theta), \, \alpha \leq \theta \leq \beta\}\), si, tenemos
\[\iiint_E f(\rho,\theta,\varphi) dV = \int_{\alpha}^{\beta} \int_{g_1(\theta)}^{g_2(\theta)} \int_{u_1(\rho,\theta)}^{u_2(\rho,\theta)} f(\rho,\theta,\varphi ) \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta. \nonumber \]
Fórmulas similares ocurren para proyecciones en los otros planos de coordenadas.
Establecer una integral para el volumen de la región delimitada por el cono\(z = \sqrt{3(x^2 + y^2)}\) y el hemisferio\(z = \sqrt{4 - x^2 - y^2}\) (ver la figura a continuación).
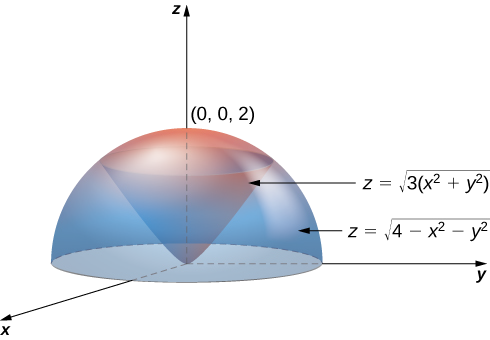
Solución
Usando las fórmulas de conversión de coordenadas rectangulares a coordenadas esféricas, tenemos:
Para el cono:\(z = \sqrt{3(x^2 + y^2)}\) o\(\rho \, \cos \, \varphi = \sqrt{3} \rho \, \sin \, \varphi\) o\(\tan \, \varphi = \frac{1}{\sqrt{3}}\) o\(\varphi = \frac{\pi}{6}\).
Para la esfera:\(z = \sqrt{4 - x^2 - y^2}\) o\(z^2 + x^2 + y^2 = 4\) o\(\rho^2 = 4\) o\(\rho = 2\).
Así, la triple integral para el volumen es
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi+\pi/6} \int_{\rho=0}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Establecer una triple integral para el volumen de la región sólida delimitada arriba por la esfera\(\rho = 2\) y delimitada por debajo por el cono\(\varphi = \pi/3\).
- Pista
-
Sigue los pasos del ejemplo anterior.
- Contestar
-
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/3} \int_{\rho=0}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta \nonumber \]
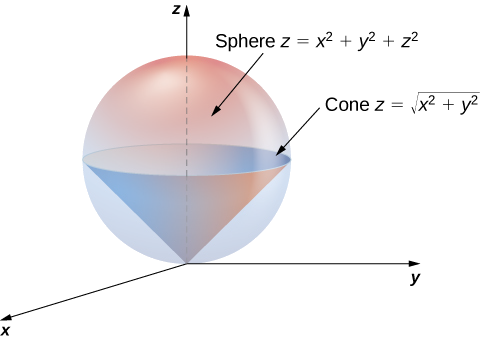
Dejar\(E\) ser la región delimitada abajo por el cono\(z = \sqrt{x^2 + y^2}\) y arriba por la esfera\(z = x^2 + y^2 + z^2\) (Figura 15.5.10). Configura una triple integral en coordenadas esféricas y encuentra el volumen de la región usando los siguientes órdenes de integración:
- \(d\rho \, d\phi \, d\theta\)
- \(d\varphi \, d\rho \, d\theta\)
Solución
a. Utilice las fórmulas de conversión para escribir las ecuaciones de la esfera y el cono en coordenadas esféricas.
Para la esfera:
\[\begin{align} x^2 + y^2 + z^2 = z \\\rho^2 = \rho \, \cos \, \varphi \\\rho = \cos \, \varphi. \end{align} \nonumber \]
Para el cono:
\[\begin{align} z = \sqrt{x^2 + y^2}\\\rho \, \cos \, \varphi = \sqrt{\rho^2 \sin^2 \, \varphi \, \cos^2 \phi } \\ \rho \, \cos \, \varphi = \sqrt{\rho^2 \sin^2 \varphi \, (\cos^2\phi + \sin^2 \phi)}\\ \rho \, \cos \, \varphi = \rho \, \sin \, \varphi\\ \cos \, \varphi = \sin \, \varphi\\ \varphi = \pi/4. \end{align} \nonumber \]
De ahí que la integral para el volumen de la región sólida\(E\) se convierte en
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\varphi=0}^{\varphi=\pi/4} \int_{\rho=0}^{\rho=\cos \, \varphi} \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
b. Considerar el\(\varphi\rho\) -plano. Tenga en cuenta que los rangos para\(\varphi\) y\(\rho\) (de la parte a.) son
\[\begin{align} 0\leq \rho \sqrt{2}/2 \text{and}\, \sqrt{2} \leq \rho 1 \\ 0 \leq \varphi \leq \pi/4 0 \leq \rho \leq \cos \, \varphi \end{align} \nonumber \]
La curva\(\rho = \cos \, \varphi\) se encuentra con la línea\(\varphi = \pi/4\) en el punto\((\pi/4,\sqrt{2}/2)\). Así, para cambiar el orden de integración, necesitamos usar dos piezas:
\[0 \leq \rho \leq \sqrt{2}/2, \, 0 \leq \varphi \leq \pi/4 \nonumber \]y
\[\sqrt{2}/2 \leq \rho \leq 1, \, 0 \leq \varphi \leq \cos^{-1} \rho. \nonumber \]
De ahí que la integral para el volumen de la región sólida\(E\) se convierte en
\[V(E) = \int_{\theta=0}^{\theta=2\pi} \int_{\rho=0}^{\rho=\sqrt{2}/2} \int_{\varphi=0}^{\varphi=\pi/4} \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta + \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\sqrt{2}/2}^{\rho=1} \int_{\varphi=0}^{\varphi=\cos^{-1}\rho} \rho^2 \sin \, \varphi \, d\varphi \, d\rho \, d\theta \nonumber \]
En cada caso, la integración resulta en\(V(E) = \frac{\pi}{8}\).
Antes de terminar esta sección, presentamos un par de ejemplos que pueden ilustrar la conversión de coordenadas rectangulares a coordenadas cilíndricas y de coordenadas rectangulares a coordenadas esféricas.
Convierta la siguiente integral en coordenadas cilíndricas:
\[\int_{y=-1}^{y=1} \int_{x=0}^{x=\sqrt{1-y^2}} \int_{z=x^2+y^2}^{z=\sqrt{x^2+y^2}} xyz \, dz \, dx \, dy. \nonumber \]
Solución
Los rangos de las variables son
\[\begin{align} -1 \leq y \leq y \\ 0 \leq x \leq \sqrt{1 - y^2} \\x^2 + y^2 \leq z \leq \sqrt{x^2 + y^2}. \end{align} \nonumber \]
Las dos primeras desigualdades describen la mitad derecha de un círculo de radio\(1\). Por lo tanto, los rangos para\(\theta\) y\(r\) son
\[-\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2} \, \text{and} \, 0 \leq r \leq 1. \nonumber \]
Los límites de\(z\) son\(r^2 \leq z \leq r\), por lo tanto
\[\int_{y=-1}^{y=1} \int_{x=0}^{x=\sqrt{1-y^2}} \int_{z=x^2+y^2}^{z=\sqrt{x^2+y^2}} xyz \, dz \, dx \, dy = \int_{\theta=-\pi/2}^{\theta=\pi/2} \int_{r=0}^{r=1} \int_{z=r^2}^{z=r} r(r \, \cos \theta) \, (r \, \sin \, \theta) \, z \, dz \, dr \, d\theta. \nonumber \]
Convierte la siguiente integral en coordenadas esféricas:
\[\int_{y=0}^{y=3} \int_{x=0}^{x=\sqrt{9-y^2}} \int_{z=\sqrt{x^2+y^2}}^{z=\sqrt{18-x^2-y^2}} (x^2 + y^2 + z^2) dz \, dx \, dy. \nonumber \]
Solución
Los rangos de las variables son
\[\begin{align} 0 \leq y \leq 3\\ 0 \leq x \leq \sqrt{9 - y^2} \\ \sqrt{x^2 + y^2} \leq z \leq \sqrt{18 - x^2 - y^2}. \end{align} \nonumber \]
Los dos primeros rangos de variables describen un cuarto de disco en el primer cuadrante del\(xy\) plano. De ahí el rango para\(\theta\) es\(0 \leq \theta \leq \frac{\pi}{2}\).
El límite inferior\(z = \sqrt{x^2 + y^2}\) es la mitad superior de un cono y el límite superior\(z = \sqrt{18 - x^2 - y^2}\) es la mitad superior de una esfera. Por lo tanto, tenemos\(0 \leq \rho \leq \sqrt{18}\), que es\(0 \leq \rho \leq 3\sqrt{2}\).
Para los rangos de\(\varphi\) necesitamos encontrar donde se cruzan el cono y la esfera, así resolver la ecuación
\[\begin{align} r^2 + z^2 = 18\\(\sqrt{x^2 + y^2})^2 + z^2 = 18 \\z^2 + z^2 = 18 \\2z^2 = 18 \\z^2 = 9 \\z = 3. \end{align} \nonumber \]
Esto da
\[\begin{align} 3\sqrt{2} \, \cos \, \varphi = 3 \\\cos \, \varphi = \frac{1}{\sqrt{2}} \\\varphi = \frac{\pi}{4}. \end{align} \nonumber \]
Armando esto, obtenemos
\[\int_{y=0}^{y=3} \int_{x=0}^{x=\sqrt{9-y^2}} \int_{z=\sqrt{x^2+y^2}}^{z=\sqrt{18-x^2-y^2}} (x^2 + y^2 + z^2) dz \, dx \, dy = \int_{\varphi=0}^{\varphi=\pi/4} \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=3\sqrt{2}} \rho^4 \sin \, \varphi \, d\rho \, d\theta \, d\varphi. \nonumber \]
Utilice coordenadas rectangulares, cilíndricas y esféricas para establecer integrales triples para encontrar el volumen de la región dentro de la esfera\(x^2 + y^2 + z^2 = 4\) pero fuera del cilindro\(x^2 + y^2 = 1\).
- Respuesta: Rectangular
-
\[\int_{x=-2}^{x=2} \int_{y=-\sqrt{4-x^2}}^{y=\sqrt{4-x^2}} \int_{z=-\sqrt{4-x^2-y^2}}^{z=\sqrt{4-x^2-y^2}} dz \, dy \, dx - \int_{x=-1}^{x=1} \int_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}} \int_{z=-\sqrt{4-x^2-y^2}}^{z=\sqrt{4-x^2-y^2}} dz \, dy \, dx. \nonumber \]
- Respuesta: Cylindrico
-
\[\int_{\theta=0}^{\theta=2\pi} \int_{r=1}^{r=2} \int_{z=-\sqrt{4-r^2}}^{z=\sqrt{4-r^2}} r \, dz \, dr \, d\theta. \nonumber \]
- Respuesta: Esférico
-
\[\int_{\varphi=\pi/6}^{\varphi=5\pi/6} \int_{\theta=0}^{\theta=2\pi} \int_{\rho=\csc \, \varphi}^{\rho=2} \rho^2 \sin \, \varphi \, d\rho \, d\theta \, d\varphi. \nonumber \]
Ahora que estamos familiarizados con el sistema de coordenadas esféricas, encontremos el volumen de algunas figuras geométricas conocidas, como esferas y elipsoides.
Encuentra el volumen del planetario esférico en l'Hemisphèric en Valencia, España, que mide cinco pisos de altura y tiene un radio de aproximadamente\(50\) pies, usando la ecuación\(x^2 + y^2 + z^2 = r^2\).

Solución
Calculamos el volumen de la bola en el primer octante, donde, y\(x \leq 0, \, y \leq 0\)\(z \leq 0\), usando coordenadas esféricas, y luego multiplicamos el resultado por\(8\) para simetría. Dado que consideramos la región\(D\) como el primer octante en la integral, los rangos de las variables son
\[0 \leq \varphi \leq \frac{\pi}{2}, \, 0 \leq \rho \leq r, \, 0 \leq \theta \leq \frac{\pi}{2}. \nonumber \]
Por lo tanto,
\[\begin{align} V = \iiint_D dx \, dy \, dz = 8 \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=\pi} \int_{\varphi=0}^{\varphi=\pi/2} \rho^2 \sin \, \theta \, d\varphi \, d\rho \, d\varphi \\ =8 \int_{\varphi=0}^{\varphi=\pi/2} d\varphi \int_{\rho=0}^{\rho=r} \rho^2 d\rho \int_{\theta=0}^{\theta=\pi/2} \sin \, \theta \, d\theta \\ = 8 \, \left(\frac{\pi}{2}\right) \, \left( \frac{r^3}{3} \right) \, (1) \\ =\dfrac{4}{3} \pi r^3.\end{align} \nonumber \]
Esto coincide exactamente con lo que sabíamos. Entonces, para una esfera con un radio de aproximadamente\(50\) pies, el volumen es\(\frac{4}{3} \pi (50)^3 \approx 523,600 \, ft^3\).
Para el siguiente ejemplo encontramos el volumen de un elipsoide.
Encuentra el volumen del elipsoide\(\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1\).
Solución
Nuevamente usamos la simetría y evaluamos el volumen del elipsoide usando coordenadas esféricas. Como antes, usamos el primer octante\(x \leq 0, \, y \leq 0\),\(z \leq 0\) y luego multiplicamos el resultado por\(8\).
En este caso los rangos de las variables son
\[0 \leq \varphi \leq \frac{\pi}{2} \, 0 \leq \rho \leq 1, \, \text{and} \, 0 \leq \theta \leq \frac{\pi}{2}. \nonumber \]
Además, necesitamos cambiar las coordenadas rectangulares a esféricas de esta manera:
\[x = a \rho \, \cos \, \varphi \, \sin \, \theta, \, y = b\rho \, \sin \, \varphi \, \sin \, \theta, \, \text{and} \, z = cp \, \cos \theta. \nonumber \]
Entonces el volumen del elipsoide se convierte
\[\begin{align} V = \iiint_D dx \, dy \, dz \\ = 8 \int_{\theta=0}^{\theta=\pi/2} \int_{\rho=0}^{\rho=1} \int_{\varphi=0}^{\varphi=\pi/2} abc \, \rho^2 \sin \, \theta \, d\varphi \, d\rho \, d\theta \\ \\ = 8abc \int_{\varphi=0}^{\varphi=\pi/2} d\varphi \int_{\rho=0}^{\rho=1} \rho^2 d\rho \int_{\theta=0}^{\theta=\pi/2} \sin \, \theta \, d\theta \\ = 8abc \left(\frac{\pi}{2}\right) \left( \frac{1}{3}\right) (1) \\ = \frac{4}{3} \pi abc. \end{align} \nonumber \]
Encuentra el volumen del espacio dentro del elipsoide\(\frac{x^2}{75^2} + \frac{y^2}{80^2} + \frac{z^2}{90^2} = 1\) y fuera de la esfera\(x^2 + y^2 + z^2 = 50^2\).
Solución
Este problema está directamente relacionado con la estructura de l'Hemisphèric. El volumen de espacio dentro del elipsoide y fuera de la esfera podría ser útil para encontrar el gasto de calentar o enfriar ese espacio. Podemos usar los dos ejemplos anteriores para el volumen de la esfera y elipsoide y luego sustraer.
Primero encontramos el volumen del elipsoide usando\(a = 75\) ft,\(b = 80\) ft y\(c = 90\) ft en el resultado del Ejemplo. De ahí que el volumen del elipsoide sea
\[V_{ellipsoid} = \frac{4}{3} \pi (75)(80)(90) \approx 2,262,000 \, ft^3. \nonumber \]
De Ejemplo, el volumen de la esfera es
\[V_{sphere} \approx 523,600 \, ft^3. \nonumber \]
Por lo tanto, el volumen del espacio dentro del elipsoide\(\frac{x^2}{75^2} + \frac{y^2}{80^2} + \frac{z^2}{90^2} = 1\) y fuera de la esfera\(x^2 + y^2 + z^2 = 50^2\) es aproximadamente
\[V_{Hemispheric} = V_{ellipsoid} - V_{sphere} = 1,738,400 \, ft^3. \nonumber \]
Los globos aerostáticos son un pasatiempo relajante y pacífico que mucha gente disfruta. Muchas reuniones de globos se llevan a cabo en todo el mundo, como la Albuquerque International Balloon Fiesta. El evento de Albuquerque es el festival de globos aerostáticos más grande del mundo., con más de\(500\) globos participando cada año.

Como su nombre lo indica, los globos aerostáticos utilizan aire caliente para generar elevación. (El aire caliente es menos denso que el aire más frío, por lo que el globo flota mientras el aire caliente permanezca caliente). El calor es generado por un quemador de propano suspendido debajo de la abertura de la canasta. Una vez que el globo despega, el piloto controla la altitud del globo, ya sea usando el quemador para calentar el aire y ascender o usando un respiradero cerca de la parte superior del globo para liberar aire caliente y descender. El piloto tiene muy poco control sobre dónde va el globo, sin embargo, los globos están a merced de los vientos. La incertidumbre sobre dónde terminaremos es una de las razones por las que los globos se sienten atraídos por el deporte.
En este proyecto utilizamos integrales triples para conocer más sobre los globos aerostáticos. Modelamos el globo en dos piezas. La parte superior del globo está modelada por una media esfera de radio 28
pies. El fondo del globo está modelado por un tronco de cono (piense en un cono de helado con el extremo puntiforme cortado). El radio del extremo grande del tronco es\(28\) pies y el radio del extremo pequeño del tronco es\(28\) pies. En la siguiente figura se muestra una gráfica de nuestro modelo de globo y un diagrama transversal que muestra las dimensiones.
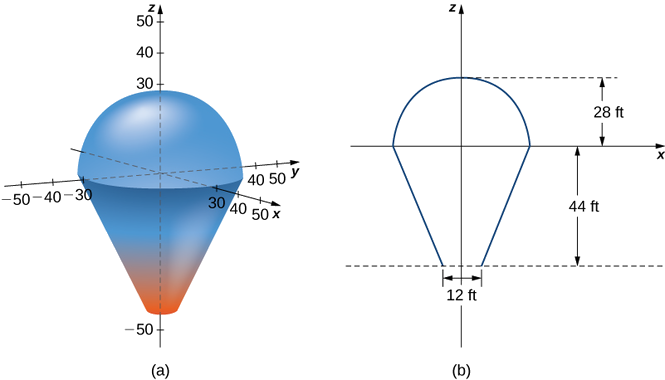
Primero queremos encontrar el volumen del globo. Si miramos la parte superior y la parte inferior del globo por separado, vemos que son sólidos geométricos con fórmulas de volumen conocidas. No obstante, todavía vale la pena configurar y evaluar las integrales que necesitaríamos para encontrar el volumen. Si calculamos el volumen usando integración, podemos usar las fórmulas de volumen conocidas para verificar nuestras respuestas. Esto ayudará a asegurar que tengamos las integrales ajustadas correctamente para las etapas posteriores y más complicadas del proyecto.
1. Encuentra el volumen del globo de dos maneras.
a. Utilice integrales triples para calcular el volumen. Considera cada parte del globo por separado. (Considere usar coordenadas esféricas para la parte superior y coordenadas cilíndricas para la parte inferior).
b. verificar la respuesta utilizando las fórmulas para el volumen de una esfera,\(V = \frac{4}{3}\pi r^3\), y para el volumen de un cono,\(V = \frac{1}{3} \pi r^2 h\).
En realidad, calcular la temperatura en un punto dentro del globo es un esfuerzo tremendamente complicado. De hecho, toda una rama de la física (termodinámica) se dedica a estudiar el calor y la temperatura. Para los fines de este proyecto, sin embargo, vamos a hacer algunas suposiciones simplificadoras sobre cómo la temperatura varía de punto a punto dentro del globo. Supongamos que justo antes del despegue, la temperatura (en grados Fahrenheit) del aire dentro del globo varía según la función\[T_0 (r,\theta,z) = \frac{z - r}{10} + 210. \nonumber \]
2. ¿Cuál es la temperatura promedio del aire en el globo justo antes del despegue? (Nuevamente, mire cada parte del globo por separado, y no olvide convertir la función en coordenadas esféricas al mirar la parte superior del globo).
Ahora el piloto activa el quemador por\(10\) segundos. Esta acción afecta la temperatura en una columna\(12\) de pies de ancho de\(20\) pies de altura, directamente por encima del quemador. Una sección transversal del globo que representa esta columna se muestra en la siguiente figura
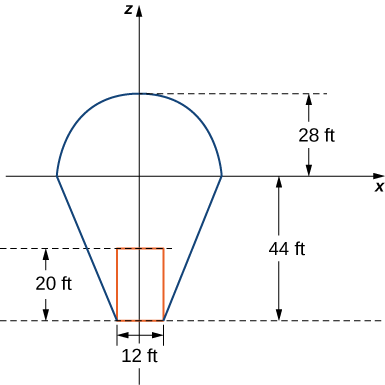
Supongamos que después de que el piloto active el quemador por\(10\) segundos, la temperatura del aire en la columna descrita anteriormente aumenta de acuerdo con la fórmula
\[H(r,\theta,z) = -2z - 48. \nonumber \]
Entonces la temperatura del aire en la columna viene dada por\[T_1(r,\theta,z) = \frac{z - r}{10} + 210 + (-2z - 48), \nonumber \]
mientras que la temperatura en el resto del globo sigue siendo dada por\[T_0(r,\theta,z) = \frac{z - r}{10} + 210. \nonumber \]
3. Encuentra la temperatura promedio del aire en el globo después de que el piloto haya activado el quemador por\(10\) segundos.
Conceptos clave
- Para evaluar una integral triple en coordenadas cilíndricas, utilice la integral iterada\[\int_{\theta=\alpha}^{\theta=\beta} \int_{r=g_1(\theta)}^{r=g_2(\theta)} \int_{z=u_1(r,\theta)}^{u_2(r,\theta)} f(r,\theta,z)r \, dz \, dr \, d\theta. \nonumber \nonumber \]
- Para evaluar una triple integral en coordenadas esféricas, utilice la integral iterada\[\int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=g_1(\theta)}^{\rho=g_2(\theta)} \int_{\varphi=u_1(r,\theta)}^{u_2(r,\theta)} f(\rho,\theta,\varphi) \, \rho^2 \sin \varphi \, d\varphi \, d\rho \, d\theta. \nonumber \nonumber \]
Ecuaciones Clave
- Triple integral en coordenadas cilíndricas\[\iiint_B g(s,y,z)dV = \iiint_B g(r \, \cos \theta, \, r \, \sin \, \theta, \, z) r \, dr \, d\theta \, dz = \iiint_B f(r,\theta,z) r \, dr \, d\theta \, dz \nonumber \]
- Triple integral en coordenadas esféricas\[\iiint_B f(\rho,\theta,\varphi) \rho^2 \sin \varphi \, d\rho \, d\varphi \, d\theta = \int_{\varphi=\gamma}^{\varphi=\psi} \int_{\theta=\alpha}^{\theta=\beta} \int_{\rho=a}^{\rho=b} f(\rho, \theta, \varphi) \rho^2 \sin \, \varphi \, d\rho \, d\varphi \, d\theta\nonumber \]
Glosario
- triple integral en coordenadas cilíndricas
-
el límite de una suma triple de Riemann, siempre que exista el siguiente límite:
\[lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(r_{ijk}^*, \theta_{ijk}^*, s_{ijk}^*) r_{ijk}^* \Delta r \Delta \theta \Delta z \nonumber \]
- triple integral en coordenadas esféricas
-
el límite de una suma triple de Riemann, siempre que exista el siguiente límite:
\[lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(\rho_{ijk}^*, \theta_{ijk}^*, \varphi_{ijk}^*) (\rho_{ijk}^*)^2 \sin \, \varphi \Delta \rho \Delta \theta \Delta \varphi \nonumber \]



Sea E la región delimitada por debajo por el\(r\theta\) plano, arriba por la esfera\(x^2 + y^2 + z^2 = 4\) y en los lados por el cilindro\(x^2 + y^2 = 1\) (Figura 15.5.5). Configura una triple integral en coordenadas cilíndricas para encontrar el volumen de la región utilizando los siguientes órdenes de integración, y en cada caso encontrar el volumen y verificar que las respuestas sean las mismas: