15.6: Cálculo de Centros de Masa y Momentos de Inercia

Objetivos de aprendizaje

• Utilice integrales dobles para ubicar el centro de masa de un objeto bidimensional.
• Utilice integrales dobles para encontrar el momento de inercia de un objeto bidimensional.
• Utilice integrales triples para ubicar el centro de masa de un objeto tridimensional.

Ya hemos discutido algunas aplicaciones de múltiples integrales, como encontrar áreas, volúmenes y el valor promedio de una función sobre una región delimitada. En esta sección desarrollamos técnicas computacionales para encontrar el centro de masa y momentos de inercia de varios tipos de objetos físicos, utilizando dobles integrales para una lámina (placa plana) y triples integrales para un objeto tridimensional con densidad variable. La densidad suele considerarse como un número constante cuando la lámina o el objeto es homogéneo; es decir, el objeto tiene densidad uniforme.

Centro de masa en dos dimensiones

El centro de masa también se conoce como el centro de gravedad si el objeto se encuentra en un campo gravitacional uniforme. Si el objeto tiene densidad uniforme, el centro de masa es el centro geométrico del objeto, que se denomina centroide. La figura\(\PageIndex{1}\) muestra un punto\(P\) como el centro de masa de una lámina. La lámina está perfectamente equilibrada alrededor de su centro de masa.

Figura\(\PageIndex{1}\): Una lámina está perfectamente equilibrada en un husillo si el centro de masa de la lámina se asienta sobre el husillo.

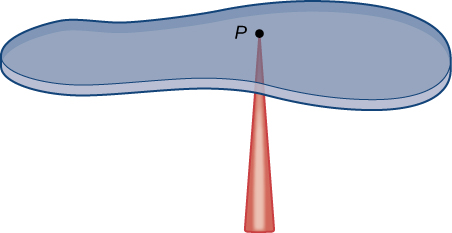
Para encontrar las coordenadas del centro de masa\(P(\bar{x},\bar{y})\) de una lámina, necesitamos encontrar el momento\(M_x\) de la lámina alrededor del\(x\) eje -y el momento\(M_y\) alrededor del\(y\) eje -eje. También necesitamos encontrar la masa\(m\) de la lámina. Entonces

\[\bar{x} = \dfrac{M_y}{m} \nonumber \]

y

\[\bar{y} = \dfrac{M_x}{m}. \nonumber \]

Consulte Momentos y Centros de Masa para conocer las definiciones y los métodos de integración única para encontrar el centro de masa de un objeto unidimensional (por ejemplo, una varilla delgada). Aquí vamos a usar una idea similar excepto que el objeto es una lámina bidimensional y usamos una doble integral.

Si permitimos una función de densidad constante, entonces\(\bar{x} = \dfrac{M_y}{m}\) y\(\bar{y} = \dfrac{M_x}{m}\) damos el centroide de la lámina.

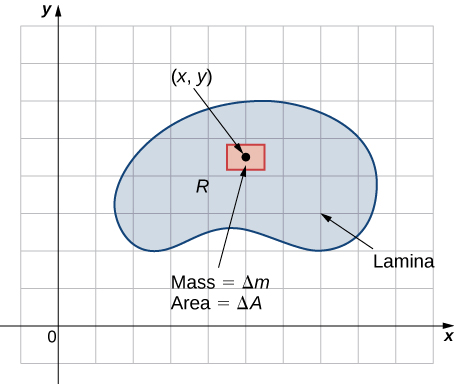
Supongamos que la lámina ocupa una región\(R\) en el\(xy\) plano -y deja\(\rho (x,y)\) ser su densidad (en unidades de masa por unidad de área) en cualquier punto\((x,y)\). Por lo tanto,

\[\rho(x,y) = \lim_{\Delta A \rightarrow 0} \dfrac{\Delta m}{\Delta A} \nonumber \]

donde\(\Delta m\) y\(\Delta A\) son la masa y área de un pequeño rectángulo que contiene el punto\((x,y)\) y el límite se toma como van las dimensiones del rectángulo a\(0\) (ver la siguiente figura).

Figura\(\PageIndex{2}\): La densidad de una lámina en un punto es el límite de su masa por área en un pequeño rectángulo alrededor del punto a medida que el área va a cero.

Al igual que antes, dividimos la región\(R\) en pequeños rectángulos\(R_{ij}\) con área\(\Delta A\) y elegimos\((x_{ij}^*, y_{ij}^*)\) como puntos de muestra. Entonces la masa\(m_{ij}\) de cada uno\(R_{ij}\) es igual a\(\rho (x_{ij}^*, y_{ij}^*) \Delta A\) (Figura\(\PageIndex{2}\)). Dejar\(k\) y\(l\) ser el número de subintervalos en\(x\) y\(y\) respectivamente. Además, tenga en cuenta que la forma podría no ser siempre rectangular pero el límite funciona de todos modos, como se vio en secciones anteriores.

Figura\(\PageIndex{3}\): Subdividiendo la lámina en pequeños rectángulos\(R_{ij}\) cada uno conteniendo un punto de muestra\((x_{ij}^*,y_{ij}^*)\).

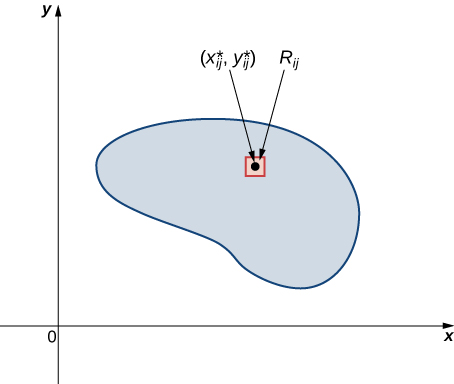
Por lo tanto, la masa de la lámina es

\[m =\lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l \rho(x_{ij}^*,y_{ij}^*) \Delta A = \iint_R \rho(x,y) dA. \nonumber \]

Veamos ahora un ejemplo de encontrar la masa total de una lámina triangular.

Ejemplo\(\PageIndex{1}\): Finding the Total Mass of a Lamina

Considera una lámina triangular\(R\) con vértices\((0,0), \, (0,3), \, (3,0)\) y con densidad\(\rho(x,y) = xy \, kg/m^2\). Encuentra la masa total.

Solución

Un boceto de la región siempre\(R\) es útil, como se muestra en la siguiente figura.

Figura\(\PageIndex{4}\): Una lámina en el\(xy\) plano con densidad\(\rho (x,y) = xy\).

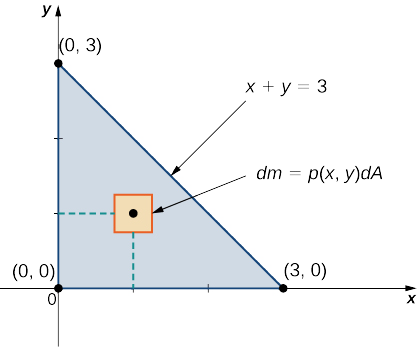
Usando la expresión desarrollada para la masa, vemos que

\[m = \iint_R \, dm = \iint_R \rho (x,y) dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} xy \, dy \, dx = \int_{x=0}^{x=3} \left[ \left. x \dfrac{y^2}{2} \right|_{y=0}^{y=3} \right] \, dx = \int_{x=0}^{x=3} \dfrac{1}{2} x (3 - x)^2 dx = \left.\left[ \dfrac{9x^2}{4} - x^3 + \dfrac{x^4}{8} \right]\right|_{x=0}^{x=3} = \dfrac{27}{8}. \nonumber \]

El cómputo es sencillo, dando la respuesta\(m = \dfrac{27}{8} \, kg\).

Ejercicio\(\PageIndex{1}\)

Considera la\(R\) misma región que en el ejemplo anterior, y usa la función de densidad\(\rho (x,y) = \sqrt{xy}\). Encuentra la masa total.

Contestar

\(\dfrac{9\pi}{8} \, kg\)

Ahora que hemos establecido la expresión para la masa, tenemos las herramientas que necesitamos para calcular momentos y centros de masa. El momento\(M_z\) alrededor del\(x\) eje para\(R\) es el límite de las sumas de momentos de las regiones\(R_{ij}\) alrededor del\(x\) eje. De ahí

\[M_x = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) \rho(x_{ij}^*,y_{ij}^*) \,\Delta A = \iint_R y\rho (x,y) \,dA \nonumber \]

De igual manera, el momento\(M_y\) alrededor\(y\) del eje para\(R\) es el límite de las sumas de momentos de las regiones\(R_{ij}\) alrededor del\(y\) eje -eje. De ahí

\[M_y = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)m_{ij} = \lim_{k,l \rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) \rho(x_{ij}^*,y_{ij}^*) \,\Delta A = \iint_R x\rho (x,y) \,dA \nonumber \]

Ejemplo\(\PageIndex{2}\): Finding Moments

Considera la misma lámina triangular\(R\) con vértices\((0,0), \, (0,3), \, (3,0)\) y con densidad\(\rho (x,y) = xy\). Encuentra los momentos\(M_x\) y\(M_y\).

Solución

Usa integrales dobles para cada momento y calcula sus valores:

\[M_x = \iint_R y\rho (x,y) \,dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} x y^2 \, dy \, dx = \dfrac{81}{20}, \nonumber \]

\[M_y = \iint_R x\rho (x,y) \,dA = \int_{x=0}^{x=3} \int_{y=0}^{y=3-x} x^2 y \, dy \, dx = \dfrac{81}{20}, \nonumber \]

El cómputo es bastante sencillo.

Ejercicio\(\PageIndex{2}\)

Considera la\(R\) misma lámina que la anterior y usa la función de densidad\(\rho (x,y) = \sqrt{xy}\). Encuentra los momentos\(M_x\) y\(M_y\).

Contestar

\(M_x = \dfrac{81\pi}{64}\)y\(M_y = \dfrac{81\pi}{64}\)

Finalmente estamos listos para reafirmar las expresiones para el centro de masa en términos de integrales. Denotamos la coordenada x del centro de masa por\(\bar{x}\) y la coordenada y por\(\bar{y}\). Específicamente,

\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} \nonumber \]

y

\[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} \nonumber \]

Ejemplo\(\PageIndex{3}\): center of mass

Consideremos nuevamente la misma región triangular\(R\) con vértices\((0,0), \, (0,3), \, (3,0)\) y con función de densidad\(\rho (x,y) = xy\). Encuentra el centro de masa.

Solución

Usando las fórmulas que desarrollamos, tenemos

\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{81/20}{27/8} = \dfrac{6}{5}, \nonumber \]

\[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{81/20}{27/8} = \dfrac{6}{5}. \nonumber \]

Por lo tanto, el centro de masa es el punto\(\left(\dfrac{6}{5},\dfrac{6}{5}\right).\)

Análisis

Si elegimos la densidad\(\rho(x,y)\) para que sea uniforme en toda la región (es decir, constante), como el valor 1 (cualquier constante servirá), entonces podemos calcular el centroide,

\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R \,dA} = \dfrac{9/2}{9/2} = 1, \nonumber \]

\[y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R \,dA} = \dfrac{9/2}{9/2} = 1. \nonumber \]

Observe que el centro de masa no\(\left(\dfrac{6}{5},\dfrac{6}{5}\right)\) es exactamente el mismo que el centroide\((1,1)\) de la región triangular. Esto se debe a la densidad variable de\(R\) Si la densidad es constante, entonces solo usamos\(\rho(x,y) = c\) (constante). Este valor se cancela de las fórmulas, por lo que para una densidad constante, el centro de masa coincide con el centroide de la lámina.

Ejercicio\(\PageIndex{3}\)

Nuevamente use la\(R\) misma región que la anterior y use la función de densidad\(\rho (x,y) = \sqrt{xy}\). Encuentra el centro de masa.

Contestar

\(\bar{x} = \dfrac{M_y}{m} = \dfrac{81\pi/64}{9\pi/8} = \dfrac{9}{8}\)y\(\bar{y} = \dfrac{M_x}{m} = \dfrac{81\pi}{9\pi/8} = \dfrac{0}{8}\).

Una vez más, a partir de los comentarios al final de Ejemplo \(\PageIndex{3}\), tenemos expresiones para el centroide de una región en el plano:

\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R \,dA} \, \text{and} \, y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R \,dA}. \nonumber \]

Deberíamos usar estas fórmulas y verificar el centroide de la región triangular RR" role="presentation" style="position:relative;" tabindex="0">R a que se hace referencia en los últimos tres ejemplos.

Ejemplo\(\PageIndex{4}\): Finding Mass, Moments, and Center of Mass

Encuentra la masa, los momentos y el centro de masa de la lámina de densidad\(\rho(x,y) = x + y\) que ocupa la región\(R\) bajo la curva\(y = x^2\) en el intervalo\(0 \leq x \leq 2\) (ver la siguiente figura).

Figura\(\PageIndex{5}\): Localización del centro de masa de una lámina\(R\) con densidad\(\rho(x,y) = x+y\).

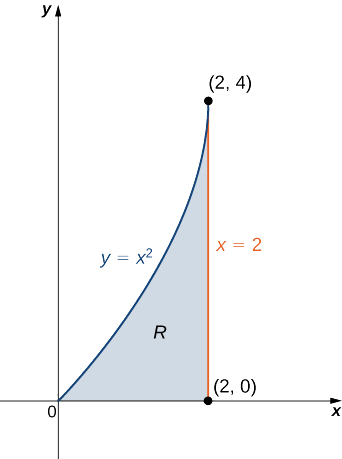
Solución

Primero calculamos la masa\(m\). Necesitamos describir la región entre la gráfica de\(y = x^2\) y las líneas verticales\(x = 0\) y\(x = 2\):

\[m = \iint_R \,dm = \iint_R \rho (x,y) \,dA = \int_{x=0}{x=2} \int_{y=0}^{y=x^2} (x + y) dy \, dx = \int_{x=0}^{x=2} \left[\left. xy + \dfrac{y^2}{2}\right|_{y=0}^{y=x^2} \right] \,dx \nonumber \]

\[= \int_{x=0}^{x=2} \left[ x^3 + \dfrac{x^4}{2} \right] dx = \left.\left[ \dfrac{x^4}{4} + \dfrac{x^5}{10}\right] \right|_{x=0}^{x=2} = \dfrac{36}{5}. \nonumber \]

Ahora computa los momentos\(M_x\) y\(M_y\):

\[M_x = \iint_R y \rho (x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x^2} y(x + y) \,dy \, dx = \dfrac{80}{7}, \nonumber \]

\[M_y = \iint_R x \rho (x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x^2} x(x + y) \,dy \, dx = \dfrac{176}{15}. \nonumber \]

Finalmente, evaluar el centro de masa,

\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x \rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{176/15}{36/5} = \dfrac{44}{27}, \nonumber \]

\[\bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y \rho (x,y) \,dA}{\iint_R \rho (x,y)\,dA} = \dfrac{80/7}{36/5} = \dfrac{100}{63}. \nonumber \]

De ahí que el centro de masa sea\((\bar{x},\bar{y}) = \left(\dfrac{44}{27}, \dfrac{100}{63} \right)\).

Ejercicio\(\PageIndex{4}\)

Calcular la masa, los momentos y el centro de masa de la región entre las curvas\(y = x\) y\(y = x^2\) con la función de densidad\(\rho(x,y) = x\) en el intervalo\(0 \leq x \leq 1\).

Contestar

\(\bar{x} = \dfrac{M_y}{m} = \dfrac{1/20}{1/12} = \dfrac{3}{5}\)y\(\bar{y} = \dfrac{M_x}{m} = \dfrac{1/24}{1/12} = \dfrac{1}{2}\)

Ejemplo\(\PageIndex{5}\): Finding a Centroid

Encuentra el centroide de la región bajo la curva\(y = e^x\) a lo largo del intervalo\(1 \leq x \leq 3\) (Figura\(\PageIndex{6}\)).

Figura\(\PageIndex{6}\): Encontrar un centroide de una región por debajo de la curva\(y = e^x\).

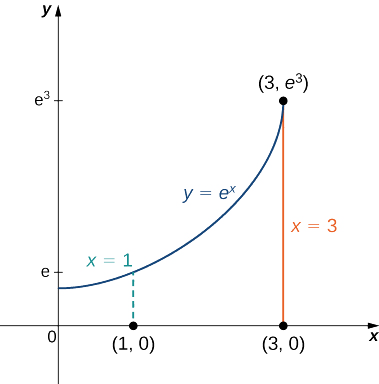
Solución

Para calcular el centroide, asumimos que la función de densidad es constante y, por lo tanto, cancela:

\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} \, and \, y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA}, \nonumber \]

\[x_c = \dfrac{M_y}{m} = \dfrac{\iint_R x \, dA}{\iint_R dA} = \dfrac{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} x \, dy \, dx}{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} \,dy \, dx} = \dfrac{\int_{x=1}^{x=3} xe^x dx}{\int_{x=1}^{x=3} e^x dx} = \dfrac{2e^3}{e^3 - e} = \dfrac{2e^2}{e^2 - 1}, \nonumber \]

\[y_c = \dfrac{M_x}{m} = \dfrac{\iint_R y \, dA}{\iint_R dA} = \dfrac{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} y \, dy \, dx}{\int_{x=1}^{x=3} \int_{y=0}^{y=e^x} \,dy \, dx} = \dfrac{\int_{x=1}^{x=3} \dfrac{e^{2x}}{2} dx}{\int_{x=1}^{x=3} e^x dx} =\dfrac{\dfrac{1}{4} e^2 (e^4 - 1)}{e(e^2 - 1)} = \dfrac{1}{4} e(e^2 + 1). \nonumber \]

Así el centroide de la región es

\[(x_c,y_c) = \left( \dfrac{2e^2}{e^2 - 1}, \dfrac{1}{4} e(e^2 + 1)\right). \nonumber \]

Ejercicio\(\PageIndex{5}\)

Calcular el centroide de la región entre las curvas\(y = x\) y\(y = \sqrt{x}\) con densidad uniforme en el intervalo\(0 \leq x \leq 1\).

Contestar

\(x_c = \dfrac{M_y}{m} = \dfrac{1/15}{1/6} = \dfrac{2}{5}\)y\( y_c = \dfrac{M_x}{m} = \dfrac{1/12}{1/6} = \dfrac{1}{2}\)

Momentos de inercia

Para una comprensión clara de cómo calcular los momentos de inercia utilizando dobles integrales, necesitamos volver a la definición general en la Sección\(6.6\). El momento de inercia de una partícula de masa\(m\) alrededor de un eje es\(mr^2\) donde\(r\) está la distancia de la partícula desde el eje. Podemos ver en Figura\(\PageIndex{3}\) que el momento de inercia del subrectángulo\(R_{ij}\) alrededor del\(x\) eje es\((y_{ij}^*)^2 \rho(x_{ij}^*,y_{ij}^*) \Delta A\). De igual manera, el momento de inercia del subrectángulo\(R_{ij}\) alrededor del\(y\) eje es\((x_{ij}^*)^2 \rho(x_{ij}^*,y_{ij}^*) \Delta A\). El momento de inercia está relacionado con la rotación de la masa; específicamente, mide la tendencia de la masa a resistir un cambio en el movimiento rotacional alrededor de un eje.

El momento de inercia\(I_x\) alrededor del\(x\) eje para la región\(R\) es el límite de la suma de momentos de inercia de las regiones\(R_{ij}\) alrededor del\(x\) eje. De ahí

\[I_x = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)^2 m_{ij} = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*)^2 \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R y^2 \rho(x,y)\,dA. \nonumber \]

De igual manera, el momento de inercia\(I_y\) alrededor del\(y\) eje para\(R\) es el límite de la suma de momentos de inercia de las regiones\(R_{ij}\) alrededor del\(y\) eje -eje. De ahí

\[I_y = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)^2 m_{ij} = \lim_{k,l\rightarrow \infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*)^2 \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R x^2 \rho(x,y)\,dA. \nonumber \]

A veces, necesitamos encontrar el momento de inercia de un objeto sobre el origen, que se conoce como el momento polar de inercia. Denotamos esto por\(I_0\) y lo obtenemos sumando los momentos de inercia\(I_x\) y\(I_y\). De ahí

\[I_0 = I_x + I_y = \iint_R (x^2 + y^2) \rho (x,y) \,dA. \nonumber \]

Todas estas expresiones se pueden escribir en coordenadas polares sustituyendo\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\), y\(dA = r \, dr \, d\theta\). Por ejemplo,\(I_0 = \iint_R r^2 \rho (r \, \cos \, \theta, \, r \, \sin \, \theta)\,dA\).

Ejemplo\(\PageIndex{6}\): Finding Moments of Inertia for a Triangular Lamina

Utilice la región triangular\(R\) con vértices\((0,0), \, (2,2)\),\((2,0)\) y con densidad\(\rho (x,y) = xy\) como en ejemplos anteriores. Encuentra los momentos de inercia.

Solución

Utilizando las expresiones establecidas anteriormente para los momentos de inercia, tenemos

\[I_x = \iint_R y^2 \rho(x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x} xy^3 \,dy \, dx = \dfrac{8}{3}, \nonumber \]

\[I_y = \iint_R x^2 \rho(x,y) \,dA = \int_{x=0}^{x=2} \int_{y=0}^{y=x} x^3y \,dy \, dx = \dfrac{16}{3}, \nonumber \]

\[I_0 = \iint_R (x^2 + y^2) \rho(x,y) \,dA = \int_0^2 \int_0^x (x^2 + y^2) xy \, dy \, dx = I_x + I_y = 8 \nonumber \]

Ejercicio\(\PageIndex{6}\)

Nuevamente use la\(R\) misma región que la anterior y la función de densidad\(\rho (x,y) = \sqrt{xy}\). Encuentra los momentos de inercia.

Contestar

\[I_x = \int_{x=0}^{x=2} \int_{y=0}^{y=x} y^2 \sqrt{xy} \, dy \, dx = \dfrac{64}{35} \nonumber \]y

\[I_y = \int_{x=0}^{x=2} \int_{y=0}^{y=x} x^2 \sqrt{xy} \, dy \, dx = \dfrac{64}{35}. \nonumber \]Además,

\[I_0 = \int_{x=0}^{x=2} \int_{y=0}^{y=x} (x^2 + y^2) \sqrt{xy} \, dy \, dx = \dfrac{128}{21} \nonumber \]

Como se mencionó anteriormente, el momento de inercia de una partícula de masa\(m\) alrededor de un eje\(r\) es\(mr^2\) donde está la distancia de la partícula desde el eje, también conocido como el radio de giro.

De ahí que los radios de giro con respecto al\(x\) eje -eje, el\(y\) -eje y el origen sean

\[R_x = \sqrt{\dfrac{I_x}{m}}, \, R_y = \sqrt{\dfrac{I_y}{m}}, \, and \, R_0 = \sqrt{\dfrac{I_0}{m}}, \nonumber \]

respectivamente. En cada caso, el radio de giro nos dice hasta qué punto (distancia perpendicular) del eje de rotación podría concentrarse toda la masa de un objeto. Los momentos de un objeto son útiles para encontrar información sobre el equilibrio y el par del objeto alrededor de un eje, pero los radios de giro se utilizan para describir la distribución de la masa alrededor de su eje centroidal. Hay muchas aplicaciones en ingeniería y física. En ocasiones es necesario encontrar el radio de giro, como en el siguiente ejemplo.

Ejemplo\(\PageIndex{7}\): Finding the Radius of Gyration for a Triangular Lamina

Considera la misma lámina triangular\(R\) con vértices\((0,0), \, (2,2)\),\((2,0)\) y con densidad\(\rho(x,y) = xy\) que en los ejemplos anteriores. Encuentra los radios de giro con respecto al\(x\) eje -eje el eje\(y\) -eje y el origen.

Solución

Si calculamos la masa de esta región nos encontramos con eso\(m = 2\). Encontramos los momentos de inercia de esta lámina en Ejemplo\(\PageIndex{4}\). A partir de estos datos, los radios de giro con respecto al\(x\) eje,\(y\) eje y origen son, respectivamente,

\[\begin{align} R_x = \sqrt{\dfrac{I_x}{m}} = \sqrt{\dfrac{8/3}{2}} = \sqrt{\dfrac{8}{6}} = \dfrac{2\sqrt{3}}{3},\\R_y = \sqrt{\dfrac{I_y}{m}} = \sqrt{\dfrac{16/3}{2}} = \sqrt{\dfrac{8}{3}} = \dfrac{2\sqrt{6}}{3}, \\R_0 = \sqrt{\dfrac{I_0}{m}} = \sqrt{\dfrac{8}{2}} = \sqrt{4} = 2.\end{align} \nonumber \]

Ejercicio\(\PageIndex{7}\)

Utilice la misma región\(R\) de Ejemplo\(\PageIndex{7}\) y la función de densidad\(\rho (x,y) = \sqrt{xy}\). Encuentra los radios de giro con respecto al\(x\) eje -eje, el\(y\) eje -y el origen.

Pista

Sigue los pasos que se muestran en el ejemplo anterior.

Contestar

\(R_x = \dfrac{6\sqrt{35}}{35}, \, R_y = \dfrac{6\sqrt{15}}{15},\)y\(R_0 = \dfrac{4\sqrt{42}}{7}\).

Centro de Masa y Momentos de Inercia en Tres Dimensiones

Todas las expresiones de dobles integrales discutidas hasta ahora pueden ser modificadas para convertirse en integrales triples.

Definición

Si tenemos un objeto sólido\(Q\) con una función de densidad\(\rho(x,y,z)\) en cualquier punto\((x,y,z)\) del espacio, entonces su masa es

\[m = \iiint_Q \rho(x,y,z) \,dV. \nonumber \]

Sus momentos sobre el\(xy\) -plano el\(xz\) -avión y el\(yz\) -plano son

\[M_{xy} = \iiint_Q z\rho (x,y,z) \,dV, \, M_{xz} = \iiint_Q y\rho(x,y,z) \,dV, \, M_{yz} = \iiint_Q x\rho(x,y,z) \,dV. \nonumber \]

Si el centro de masa del objeto es el punto\((\bar{x}, \bar{y}, \bar{z})\), entonces

\[\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}. \nonumber \]

Además, si el objeto sólido es homogéneo (con densidad constante), entonces el centro de masa se convierte en el centroide del sólido. Finalmente, los momentos de inercia sobre el\(yz\) -plano,\(xz\) -plano, y el\(xy\) -plano son

\[I_x = \iiint_Q (y^2 + z^2) \, \rho (x,y,z) \, dV, \nonumber \]

\[I_y = \iiint_Q (x^2 + z^2) \, \rho (x,y,z) \, dV, \nonumber \]

\[I_z = \iiint_Q (x^2 + y^2) \, \rho (x,y,z) \, dV. \nonumber \]

Ejemplo\(\PageIndex{8}\): Finding the Mass of a Solid

Supongamos que\(Q\) es una región sólida delimitada por\(x + 2y + 3z = 6\) y los planos de coordenadas y tiene densidad\(\rho (x,y,z) = x^2 yz\). Encuentra la masa total.

Solución

La región\(Q\) es un tetraedro (Figura\(\PageIndex{7}\)) que se encuentra con los ejes en los puntos\((6,0,0), \, (0,3,0),\) y\((0,0,2)\). Para encontrar los límites de la integración, deja\(z = 0\) entrar el plano inclinado\(z = \dfrac{1}{3} (6 - x - 2y)\). Después para\(x\) y\(y\) encontrar la proyección de\(Q\) sobre el\(xy\) -plano, que está delimitado por los ejes y la línea\(x + 2y = 6\). De ahí que la masa sea

\[m = \iiint_Q \rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=1/2(6-x)} \int_{z=0}^{z=1/3(6-x-2y)} x^2 yz \, dz \, dy \, dx = \dfrac{108}{35} \nonumber \]

Figura\(\PageIndex{7}\): Hallar la masa de un sólido tridimensional\(Q\).

Ejercicio\(\PageIndex{8}\)

Considere la misma región\(Q\) (Figura\(\PageIndex{7}\)), y utilice la función de densidad\(\rho (x,y,z) = xy^2z\). Encuentra la misa.

Pista

Sigue los pasos del ejemplo anterior.

Contestar

\(\dfrac{54}{35} = 1.543\)

Ejemplo\(\PageIndex{9}\): Finding the Center of Mass of a Solid

Supongamos que\(Q\) es una región sólida delimitada por el plano\(x + 2y + 3z = 6\) y los planos de coordenadas con densidad\(\rho (x,y,z) = x^2yz\) (ver Figura\(\PageIndex{7}\)). Encuentra el centro de masa usando aproximación decimal.

Solución

Hemos utilizado este tetraedro antes y conocemos los límites de la integración, por lo que podemos proceder a los cálculos de inmediato. Primero, necesitamos encontrar los momentos sobre el\(xy\) -avión, el\(xz\) -avión, y el\(yz\) -plano:

\[M_{xy} = \iiint_Q z\rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} x^2 yz^2 \,dz \, dy \, dx = \dfrac{54}{35} \approx 1.543, \nonumber \]

\[M_{xz} = \iiint_Q y\rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} x^2 y^2z \, dz \, dy \, dx = \dfrac{81}{35} \approx 2.314, \nonumber \]

\[M_{yz} = \iiint_Q x\rho (x,y,z) \,dV = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} x^3 yz \, dz \, dy \, dx = \dfrac{243}{35} \approx 6.943. \nonumber \]

De ahí que el centro de masa sea

\[\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}, \nonumber \]

\[\bar{x} = \dfrac{M_{yz}}{m} = \dfrac{243/35}{108/35} = \dfrac{243}{108} = 2.25, \nonumber \]

\[\bar{y} = \dfrac{M_{xz}}{m} = \dfrac{81/35}{108/35} = \dfrac{81}{108} = 0.75, \nonumber \]

\[\bar{z} = \dfrac{M_{xy}}{m} = \dfrac{54/35}{108/35} = \dfrac{54}{108} = 0.5 \nonumber \]

El centro de masa para el tetraedro\(Q\) es el punto\((2.25, 0.75, 0.5)\).

Ejercicio\(\PageIndex{9}\)

Considera la misma región\(Q\) (Figura\(\PageIndex{7}\)) y usa la función de densidad\(\rho (x,y,z) = xy^2z\). Encuentra el centro de masa.

Pista

Verifica eso\(M_{xy} = \dfrac{27}{35}, \, M_{xz} = \dfrac{243}{140},\) y\(M_{yz} = \dfrac{81}{35}\). Luego use\(m\) de una pregunta de punto de control anterior.

Contestar

\(\left(\dfrac{3}{2}, \dfrac{9}{8}, \dfrac{1}{2}\right)\)

Concluimos esta sección con un ejemplo de encontrar momentos de inercia\(I_x, \, I_y\), y\(I_z\).

Ejemplo\(\PageIndex{10}\): Finding the Moments of Inertia of a Solid

Supongamos que\(Q\) es una región sólida y está delimitada por\(x + 2y + 3z = 6\) y los planos de coordenadas con densidad\(\rho (x,y,z) = x^2 yz\) (ver Figura\(\PageIndex{7}\)). Encuentra los momentos de inercia del tetraedro\(Q\) sobre el\(yz\) plano, el\(xz\) plano y el\(xy\) plano.

Solución

Una vez más, casi de inmediato podemos escribir los límites de la integración y de ahí que podamos proceder rápidamente a evaluar los momentos de inercia. Usando la fórmula antes señalada, los momentos de inercia del tetraedro\(Q\) alrededor del\(yz\) -plano, el\(xz\) -plano, y el\(xy\) -plano son

\[I_x = \iiint_Q (y^2 + z^2) \rho(x,y,z) \,dV, \nonumber \]

\[I_y = \iiint_Q (x^2 + z^2) \rho(x,y,z) \,dV, \nonumber \]y

\[I_z = \iiint_Q (x^2 + y^2) \rho(x,y,z) \,dV \, with \, \rho(x,y,z) = x^2yz. \nonumber \]

Procediendo con los cómputos, tenemos

\[\begin{align*} I_x = \iiint_Q (y^2 + z^2) x^2 \rho(x,y,z) \,dV \\[4pt] = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} (y^2 + z^2) x^2 yz \, dz \, dy \, dx = \dfrac{117}{35} \approx 3.343,\end{align*}\]

\[\begin{align*} I_y = \iiint_Q (x^2 + z^2) x^2 \rho(x,y,z) \,dV \\[4pt] = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} (x^2 + z^2) x^2 yz \, dz \, dy \, dx = \dfrac{684}{35} \approx 19.543, \end{align*}\]

\[\begin{align*} I_z = \iiint_Q (x^2 + y^2) x^2 \rho(x,y,z) \,dV \\[4pt] = \int_{x=0}^{x=6} \int_{y=0}^{y=\frac{1}{2}(6-x)} \int_{z=0}^{z=\frac{1}{3}(6-x-2y)} (x^2 + y^2) x^2 yz \, dz \, dy \, dx = \dfrac{729}{35} \approx 20.829. \end{align*}\]

Así, los momentos de inercia del tetraedro\(Q\) alrededor del\(yz\) -plano, el\(xz\) -plano, y el\(xy\) -plano son\(117/35, \, 684/35\), y\(729/35\), respectivamente.

Ejercicio\(\PageIndex{10}\)

Considere la misma región\(Q\) (Figura\(\PageIndex{7}\)), y utilice la función de densidad\(\rho(x,y,z) = xy^2z\). Encuentra los momentos de inercia sobre los tres planos de coordenadas.

Contestar

Los momentos de inercia del tetraedro\(Q\) alrededor del\(yz\) plano, el\(xz\) plano y el\(xy\) plano son\(99/35, \, 36/7\) y\(243/35\), respectivamente.

Conceptos clave

Encontrar la masa, el centro de masa, los momentos y los momentos de inercia en dobles integrales:

• Para una lámina\(R\) con una función de densidad\(\rho (x,y)\)\((x,y)\) en cualquier punto del plano, la masa es\[m = \iint_R \rho (x,y) \,dA. \nonumber \]
• Los momentos sobre el\(x\) eje y el\(y\) eje son\[M_x = \iint_R y\rho(x,y) \,dA \, and \, M_y = \iint_R x\rho(x,y) \,dA. \nonumber \]
• El centro de masa está dado por\(\bar{x} = \dfrac{M_y}{m}, \, \bar{y} = \dfrac{M_x}{m}\).
• El centro de masa se convierte en el centroide del plano cuando la densidad es constante.
• Los momentos de inercia alrededor del\(x\) eje -eje,\(y\) -eje, y el origen son\[I_x = \iint_R y^2 \rho(x,y) \,dA, \, I_y = \iint_R x^2 \rho(x,y) \,dA, \, and \, I_0 = I_x + I_y = \iint_R (x^2 + y^2) \rho(x,y) \,dA. \nonumber \]

Encontrar la masa, el centro de masa, los momentos y los momentos de inercia en triples integrales:

• Para un objeto sólido\(Q\) con una función de densidad\(\rho(x,y,z)\) en cualquier punto\((x,y,z)\) del espacio, la masa es\[m = \iiint_Q \rho (x,y,z) \,dV. \nonumber \]
• Los momentos sobre el\(xy\) avión, el\(xz\) plano y el\(yz\) plano son\[M_{xy} = \iiint_Q z\rho (x,y,z)\,dV, \, M_{xz} = \iiint_Q y\rho (x,y,z)\,dV, \, M_{yz} = \iiint_Q x\rho (x,y,z)\,dV \nonumber \]
• El centro de masa está dado por\(\bar{x} = \dfrac{M_{yz}}{m}, \, \bar{y} = \dfrac{M_{xz}}{m}, \, \bar{z} = \dfrac{M_{xy}}{m}.\)
• El centro de masa se convierte en el centroide del sólido cuando la densidad es constante.
• Los momentos de inercia sobre el\(yz\) plano, el\(xz\) plano y el\(xy\) plano son\[I_x = \iiint_Q (y^2 + z^2) \, \rho (x,y,z) \, dV, \, I_y = \iiint_Q (x^2 + z^2) \, \rho (x,y,z) \, dV, \, I_z = \iiint_Q (x^2 + y^2) \, \rho (x,y,z) \, dV. \nonumber \]

Ecuaciones Clave

• Masa de una lámina\[m = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R \rho(x,y) \,dA \nonumber \]
• Momento sobre el eje x\[M_x = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (y_{ij}^*) \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R y\rho(x,y)\,dA \nonumber \]
• Momento sobre el eje y\[M_y = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) m_{ij} = \lim_{k,l \rightarrow\infty} \sum_{i=1}^k \sum_{j=1}^l (x_{ij}^*) \rho (x_{ij}^*, y_{ij}^*) \,\Delta A = \iint_R x\rho(x,y)\,dA \nonumber \]
• Centro de masa de una lámina\[\bar{x} = \dfrac{M_y}{m} = \dfrac{\iint_R x\rho (x,y) \,dA}{\iint_R \rho (x,y) \,dA} \, and \, \bar{y} = \dfrac{M_x}{m} = \dfrac{\iint_R y\rho (x,y) \,dA}{\iint_R \rho (x,y) \,dA} \nonumber \]

Glosario

radio de giro

la distancia desde el centro de masa de un objeto hasta su eje de rotación