15.7E: Ejercicios para la Sección 15.7

Última actualización
Guardar como PDF

Page ID: 116282

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En los ejercicios 1 - 6, se da la función$T : S \rightarrow R, \space T (u,v) = (x,y)$ sobre la región$S = \big\{(u,v) \,|\, 0 \leq u \leq 1, \space 0 \leq v \leq 1\big\}$ delimitada por la unidad cuadrada, donde$R \in R^2$ está la imagen de$S$ debajo$T$.

a. Justificar que la función$T$ es una$C^1$ transformación.

b. Encuentra las imágenes de los vértices de la unidad cuadrada$S$ a través de la función$T$.

c. Determinar la imagen$R$ de la unidad cuadrada$S$ y graficarla.

1. $x = 2u, \space y = 3v$

2. $x = \frac{u}{2}, \space y = \frac{v}{3}$

Contestar

a.$T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = \frac{u}{2}$ y$y = h(u,v) = \frac{v}{3}$. Las funciones$g$ y$h$ son continuas y diferenciables, y las derivadas parciales$g_u (u,v) = \frac{1}{2}, \space g_v (u,v) = 0, \space h_u (u,v) = 0$ y$h_v (u,v) = \frac{1}{3}$ son continuas$S$;

b.$T(0,0) = (0,0), \space T(1,0) = \left(\frac{1}{2},0\right), \space T(0,1) = \left(0,\frac{1}{3}\right)$, y$T(1,1) = \left(\frac{1}{2}, \frac{1}{3} \right)$;

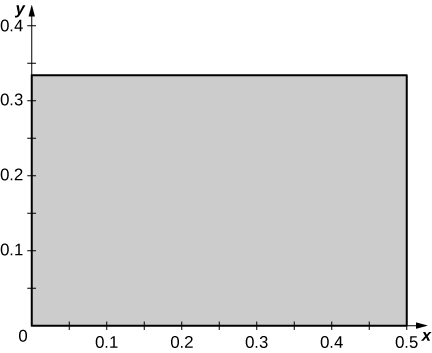
c.$R$ es el rectángulo de vértices$(0,0), \space \left(0,\frac{1}{3}\right), \space \left(\frac{1}{2}, \frac{1}{3} \right)$, y$\left(0,\frac{1}{3}\right)$ en el$xy$ plano -plano; la siguiente figura.

$Un rectángulo con una esquina en el origen, longitud horizontal 0.5 y altura vertical 0.34.$

3. $x = u - v, \space y = u + v$

4. $x = 2u - v, \space y = u + 2v$

Answer

a. $T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = 2u - v$ and $y = h(u,v) = u + 2v$. The functions $g$ and $h$ are continuous and differentiable, and the partial derivatives $g_u (u,v) = 2, \space g_v (u,v) = -1, \space h_u (u,v) = 1$ and $h_v (u,v) = 2$ are continuous on $S$;

b. $T(0,0) = (0,0), \space T(1,0) = (2,1), \space T(0,1) = (-1,2)$, and $T(1,1) = (1,3)$;

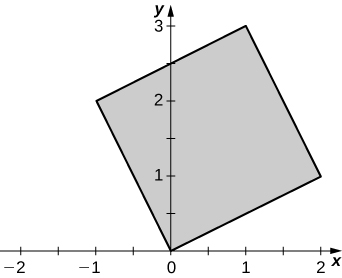
c. $R$ is the parallelogram of vertices $(0,0), \space (2,1) \space (1,3)$, and $(-1,2)$ in the $xy$-plane; the following figure.

$A square of side length square root of 5 with one corner at the origin and another at (2, 1).$

5. $x = u^2, \space y = v^2$

6. $x = u^3, \space y = v^3$

Contestar

a.$T(u,v) = (g(u,v), \space h(u,v), \space x = g(u,v) = u^3$ y$y = h(u,v) = v^3$. Las funciones$g$ y$h$ son continuas y diferenciables, y las derivadas parciales$g_u (u,v) = 3u^2, \space g_v (u,v) = 0, \space h_u (u,v) = 0$ y$h_v (u,v) = 3v^2$ son continuas$S$;

b.$T(0,0) = (0,0), \space T(1,0) = (1,0), \space T(0,1) = (0,1)$, y$T(1,1) = (1,1)$;

c.$R$ es la unidad cuadrada en el$xy$ plano -ver la figura en la respuesta al ejercicio anterior.

En los ejercicios 7 - 12, determinar si las transformaciones$T : S \rightarrow R$ son uno a uno o no.

7. $x = u^2, \space y = v^2$, donde$S$ está el rectángulo de vértices$(-1,0), \space (1,0), \space (1,1)$, y$(-1,1)$.

8. $x = u^4, \space y = u^2 + v$, donde$S$ está el triángulo de vértices$(-2,0), \space (2,0)$, y$(0,2)$.

Contestar: $T$no es uno a uno: dos puntos de$S$ tienen la misma imagen. Efectivamente,$T(-2,0) = T(2,0) = (16,4)$.

9. $x = 2u, \space y = 3v$, donde$S$ está el cuadrado de vértices$(-1,1), \space (-1,-1), \space (1,-1)$, y$(1,1)$.

10. $T(u, v) = (2u - v, u),$donde$S$ está el triángulo con vértices$(-1,1), \, (-1,-1)$, y$(1,-1)$.

Contestar: $T$es uno a uno: Argumentamos por contradicción. $T(u_1,v_1) = T(u_2,v_2)$implica$2u_1 - v_1 = 2u_2 - v_2$ y$u_1 = u_2$. Así,$u_1 = u+2$ y$v_1 = v_2$.

11. $x = u + v + w, \space y = u + v, \space z = w$, donde$S = R = R^3$.

12. $x = u^2 + v + w, \space y = u^2 + v, \space z = w$, donde$S = R = R^3$.

Contestar: $T$no es uno a uno:$T(1,v,w) = (-1,v,w)$

En los ejercicios 13 - 18, las transformaciones$T : R \rightarrow S$ son uno a uno. Encuentra sus transformaciones inversas relacionadas$T^{-1} : R \rightarrow S$.

13. $x = 4u, \space y = 5v$, donde$S = R = R^2$.

14. $x = u + 2v, \space y = -u + v$, donde$S = R = R^2$.

Contestar: $u = \frac{x-2y}{3}, \space v= \frac{x+y}{3}$

15. $x = e^{2u+v}, \space y = e^{u-v}$, donde$S = R^2$ y$R = \big\{(x,y) \,|\, x > 0, \space y > 0\big\}$

16. $x = \ln u, \space y = \ln(uv)$, donde$S = \big\{(u,v) \,|\, u > 0, \space v > 0\big\}$ y$R = R^2$.

Contestar: $u = e^x, \space v = e^{-x+y}$

17. $x = u + v + w, \space y = 3v, \space z = 2w$, donde$S = R = R^3$.

18. $x = u + v, \space y = v + w, \space z = u + w$, donde$S = R = R^3$.

Contestar: $u = \frac{x-y+z}{2}, \space v = \frac{x+y-z}{2}, \space w = \frac{-x+y+z}{2}$

En los ejercicios 19 - 22 se da la transformación$T : S \rightarrow R, \space T (u,v) = (x,y)$ y la región$R \subset R^2$. Encuentra la región$S \subset R^2$.

19. $x = au, \space y = bv, \space R = \big\{(x,y) \,|\, x^2 + y^2 \leq a^2 b^2\big\}$donde$a,b > 0$

20. $x = au, \space y = bc, \space R = \big\{(x,y) \,|\, \frac{x^2}{a^2} + \frac{y^2}{b^2} \leq 1\big\}$, donde$a,b > 0$

Contestar: $S = \big\{(u,v) \,|\, u^2 + v^2 \leq 1\big\}$

21. $x = \frac{u}{a}, \space y = \frac{v}{b}, \space z = \frac{w}{c}, \space R = \big\{(x,y)\,|\,x^2 + y^2 + z^2 \leq 1\big\}$, donde$a,b,c > 0$

22. $x = au, \space y = bv, \space z = cw, \space R = \big\{(x,y)\,|\,\frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} \leq 1, \space z > 0\big\}$, donde$a,b,c > 0$

Contestar: $R = \big\{(u,v,w)\,|\,u^2 - v^2 - w^2 \leq 1, \space w > 0\big\}$

En los ejercicios 23 - 32, encuentra al jacobiano$J$ de la transformación.

23. $x = u + 2v, \space y = -u + v$

24. $x = \frac{u^3}{2}, \space y = \frac{v}{u^2}$

Contestar: $\frac{3}{2}$

25. $x = e^{2u-v}, \space y = e^{u+v}$

26. $x = ue^v, \space y = e^{-v}$

Contestar: $-1$

27. $x = u \space \cos (e^v), \space y = u \space \sin(e^v)$

28. $x = v \space \sin (u^2), \space y = v \space \cos(u^2)$

Contestar: $2uv$

29. $x = u \space \cosh v, \space y = u \space \sinh v, \space z = w$

30. $x = v \space \cosh \left(\frac{1}{u}\right), \space y = v \space \sinh \left(\frac{1}{u}\right), \space z = u + w^2$

Contestar: $\frac{v}{u^2}$

31. $x = u + v, \space y = v + w, \space z = u$

32. $x = u - v, \space y = u + v, \space z = u + v + w$

Contestar: $2$

33. La región triangular$R$ con los vértices$(0,0), \space (1,1)$, y$(1,2)$ se muestra en la siguiente figura.

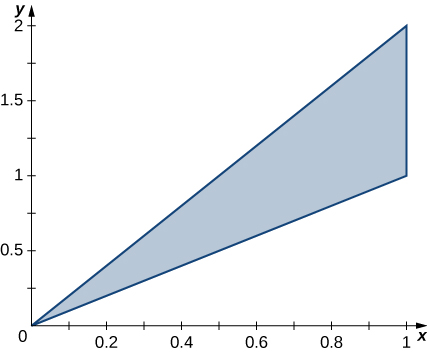
$Un triángulo con esquinas en el origen, (1, 1), y (1, 2).$

a. Encontrar una transformación$T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)$, where $a,b,c$, and $d$ are real numbers with $ad - bc \neq 0$ such that $T^{-1} (0,0) = (0,0), \space T^{-1} (1,1) = (1,0)$, and $T^{-1}(1,2) = (0,1)$.

b. Use the transformation $T$ to find the area $A(R)$ of the region $R$.

34. The triangular region $R$ with the vertices $(0,0), \space (2,0)$, and $(1,3)$ is shown in the following figure.

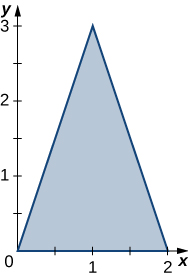
$A triangle with corners at the origin, (2, 0), and (1, 3).$

a. encontrar una transformación$T : S \rightarrow R, \space T(u,v) = (x,y) = (au + bv + dv)$, donde$a,b,c$, y$d$ son números reales con$ad - bc \neq 0$ tal que$T^{-1} (0,0) = (0,0), \space T^{-1} (2,0) = (1,0)$, y$T^{-1}(1,3) = (0,1)$.

b. Utilizar la transformación$T$ para encontrar el área$A(R)$ de la región$R$.

Contestar: a.$T (u,v) = (2u + v, \space 3v)$
b. El área de$R$ es$\displaystyle A(R) = \int_0^3 \int_{y/3}^{(6-y)/3} \, dx \, dy = \int_0^1 \int_0^{1-u} \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \, dv \space du = \int_0^1 \int_0^{1-u} 6 \, dv \, du = 3.$

En los ejercicios 35 - 36, utilice la transformación$u = y - x, \space v = y$, para evaluar las integrales en el paralelogramo$R$ de vértices$(0,0), \space (1,0), \space (2,1)$, y$(1,1)$ se muestra en la siguiente figura.

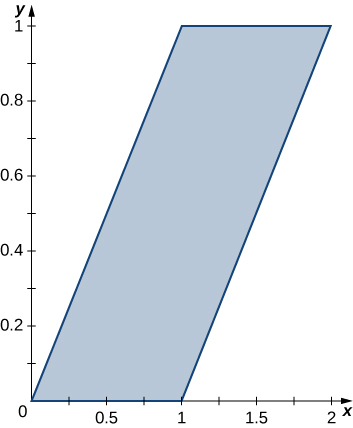
$Un rombo con esquinas en el origen, (1, 0), (1, 1) y (2, 1).$

35. $\displaystyle \iint_R (y - x) \, dA$

36. $\displaystyle \iint_R (y^2 - xy) \, dA$

Answer: $-\frac{1}{4}$

In exercises 37 - 38, use the transformation $y = x = u, \space x + y = v$ to evaluate the integrals on the square $R$ determined by the lines $y = x, \space y = -x + 2, \space y = x + 2$, and $y = -x$ shown in the following figure.

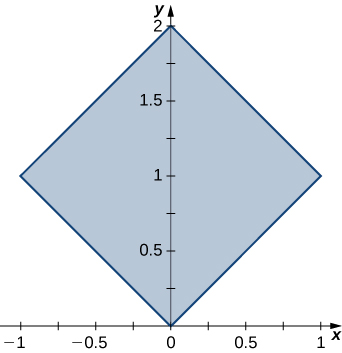
$A square with side lengths square root of 2 rotated 45 degrees with one corner at the origin and another at (1, 1).$

37. $\displaystyle \iint_R e^{x+y} \, dA$

38. $\displaystyle \iint_R \sin (x - y) \, dA$

Contestar: $-1 + \cos 2$

En los ejercicios 39 - 40, utilice la transformación$x = u, \space 5y = v$ para evaluar las integrales en la región$R$ delimitada por la elipse$x^2 + 25y^2 = 1$ mostrada en la siguiente figura.

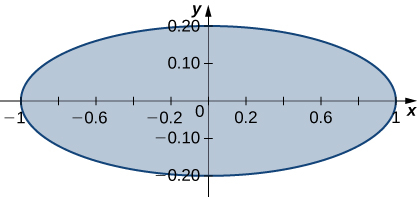
$Una elipse con centro en el origen, eje mayor 2 y menor 0.4.$

39. $\displaystyle \iint_R \sqrt{x^2 + 25y^2} \, dA$

40. $\displaystyle \iint_R (x^2 + 25y^2)^2 \, dA$

Answer: $\frac{\pi}{15}$

In exercises 41 - 42, use the transformation $u = x + y, \space v = x - y$ to evaluate the integrals on the trapezoidal region $R$ determined by the points $(1,0), \space (2,0), \space (0,2)$, and $(0,1)$ shown in the following figure.

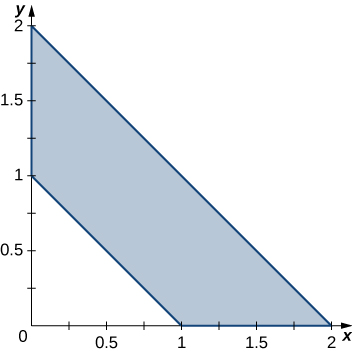
$A trapezoid with corners at (1, 0), (0, 1), (0, 2), and (2, 0).$

41. $\displaystyle \iint_R (x^2 - 2xy + y^2) \space e^{x+y} \, dA$

42. $\displaystyle \iint_R (x^3 + 3x^2y + 3xy^2 + y^3) \, dA$

Contestar: $\frac{31}{5}$

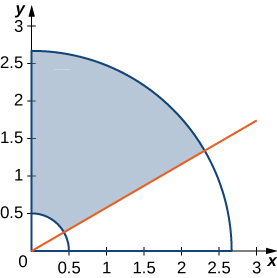
43. El sector anular circular$R$ delimitado por los círculos$4x^2 + 4y^2 = 1$ y$9x^2 + 9y^2 = 64$, la línea$x = y \sqrt{3}$, y el$y$ eje -se muestra en la siguiente figura. Encuentre una transformación$T$ de una región rectangular$S$ en el$r\theta$ plano -a la región$R$ en el$xy$ plano. Gráfica$S$.

$En el primer cuadrante, una sección de un anillo descrito por un radio interno de 0.5, radio exterior ligeramente superior a 2.5, y centrar el origen. Hay una línea que divide este anillo que proviene de aproximadamente un ángulo de 30 grados. La porción correspondiente a 60 grados está sombreada.$

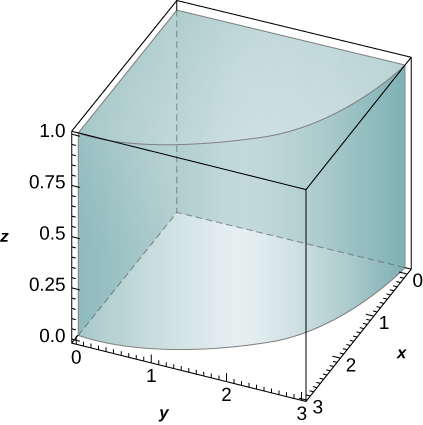
44. El sólido$R$ bounded by the circular cylinder $x^2 + y^2 = 9$ and the planes $z = 0, \space z = 1, \space x = 0$, and $y = 0$ is shown in the following figure. Find a transformation $T$ from a cylindrical box $S$ in $r\theta z$-space to the solid $R$ in $xyz$-space.

$A quarter of a cylinder with height 1 and radius 3. The center axis is the z axis.$

Contestar: $T (r,\theta,z) = (r \space \cos \theta, \space r \space \sin \theta, \space z); \space S = [0,3] \times [0,\frac{\pi}{2}] \times [0,1]$en el$r\theta z$ -espacio

45. Mostrar que\[\iint_R f \left(\sqrt{\frac{x^2}{3} + \frac{y^2}{3}}\right) dA = 2 \pi \sqrt{15} \int_0^1 f (\rho) \rho \space d\rho, \nonumber \] donde$f$ es una función continua$[0,1]$ y$R$ es la región delimitada por la elipse$5x^2 + 3y^2 = 15$.

46. Mostrar que\[\iiint_R f \left(\sqrt{16x^2 + 4y^2 + z^2}\right) dV = \frac{\pi}{2} \int_0^1 f (\rho) \rho^2 d\rho, \nonumber \] donde$f$ es una función continua$[0,1]$ y$R$ es la región delimitada por el elipsoide$16x^2 + 4y^2 + z^2 = 1$.

47. [T] Encontrar el área de la región delimitada por las curvas$xy = 1, \space xy = 3, \space y = 2x$, y$y = 3x$ mediante el uso de la transformación$u = xy$ y$v = \frac{y}{x}$. Utilice un sistema de álgebra por computadora (CAS) para graficar las curvas de contorno de la región$R$.

48. [T] Encontrar el área de la región delimitada por las curvas$x^2y = 2, \space x^2y = 3, \space y = x$, y$y = 2x$ mediante el uso de la transformación$u = x^2y$ y$v = \frac{y}{x}$. Utilice un CAS para graficar las curvas de contorno de la región$R$.

Contestar

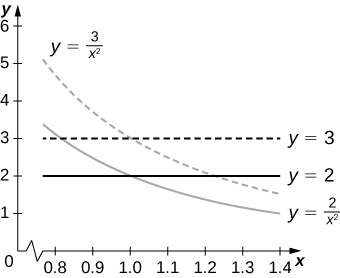
El área de$R$ es$10 - 4\sqrt{6}$; las curvas de límite de$R$ están graficadas en la siguiente figura.

$Se dibujan cuatro líneas, a saber, y = 3, y = 2, y = 3/ (x cuadrado), e y = 2/ (x cuadrado). Las líneas y = 3 e y = 2 son paralelas entre sí. Las líneas y = 3/ (x cuadrado) e y = 2/ (x cuadrado) son curvas que corren algo paralelas entre sí.$

49. Evaluar la triple integral\[\int_0^1 \int_1^2 \int_z^{z+1} (y + 1) \space dx \space dy \space dz \nonumber \] by using the transformation $u = x - z, \space v = 3y$, and $w = \frac{z}{2}$.

50. Evaluate the triple integral \[\int_0^2 \int_4^6 \int_{3z}^{3z+2} (5 - 4y) \space dx \space dy \space dz \nonumber \] by using the transformation $u = x - 3z, \space v = 4y$, and $w = z$.

Answer: $8$

51. A transformation $T : R^2 \rightarrow R^2, \space T (u,v) = (x,y)$ of the form $x = au + bv, \space y = cu + dv$, where $a,b,c$, and $d$ are real numbers, is called linear. Show that a linear transformation for which $ad - bc \neq 0$ maps parallelograms to parallelograms.

52. A transformation $T_{\theta} : R^2 \rightarrow R^2, \space T_{\theta} (u,v) = (x,y)$ of the form $x = u \space \cos \theta - v \space \sin \theta, \space y = u \space \sin \theta + v \space \cos \theta$, is called a rotation angle $\theta$. Show that the inverse transformation of $T_{\theta}$ satisfies $T_{\theta}^{-1} = T_{-\theta}$ where $T_{-\theta}$ is the rotation of angle $-\theta$.

53. [T] Find the region $S$ in the $uv$-plane whose image through a rotation of angle $\frac{\pi}{4}$ is the region $R$ enclosed by the ellipse $x^2 + 4y^2 = 1$. Use a CAS to answer the following questions.

a. Graph the region $S$.

b. Evaluate the integral $\displaystyle \iint_S e^{-2uv} \, du \, dv.$ Round your answer to two decimal places.

54. [T] The transformations $T_i : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space i = 1, . . . , 4,$ defined by $T_1(u,v) = (u,-v), \space T_2 (u,v) = (-u,v), \space T_3 (u,v) = (-u, -v)$, and $T_4 (u,v) = (v,u)$ are called reflections about the $x$-axis, $y$-axis origin, and the line $y = x$, respectively.

a. Find the image of the region $S = \big\{(u,v)\,|\,u^2 + v^2 - 2u - 4v + 1 \leq 0\big\}$ in the $xy$-plane through the transformation $T_1 \circ T_2 \circ T_3 \circ T_4$.

b. Use a CAS to graph $R$.

c. Evaluate the integral $\displaystyle \iint_S \sin (u^2) \, du \, dv$ by using a CAS. Round your answer to two decimal places.

Answer

a. $R = \big\{(x,y)\,|\,y^2 + x^2 - 2y - 4x + 1 \leq 0\big\}$;
b. $R$ is graphed in the following figure;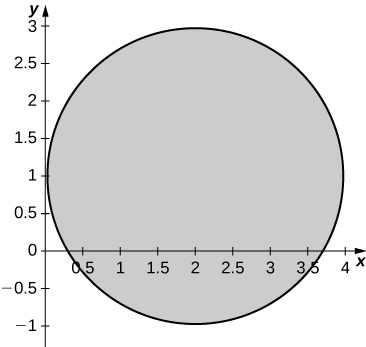

$A circle with radius 2 and center (2, 1).$

c.$3.16$

55. [T] Las transformaciones$T_{k,1,1} : \mathbb{R}^3 \rightarrow \mathbb{R}^3, \space T_{k,1,1}(u,v,w) = (x,y,z)$ de la forma$x = ku, \space y = v, \space z = w$, donde$k \neq 1$ es un número real positivo, se llama estiramiento si$k > 1$ y compresión si$0 < k < 1$ en la$x$ dirección -dirección. Utilice un CAS para evaluar la integral$\displaystyle \iiint_S e^{-(4x^2+9y^2+25z^2)} \, dx \, dy \, dz$ en el sólido$S = \big\{(x,y,z) \,|\, 4x^2 + 9y^2 + 25z^2 \leq 1\big\}$ considerando la compresión$T_{2,3,5}(u,v,w) = (x,y,z)$ definida por$x = \frac{u}{2}, \space y = \frac{v}{3}$, y$z = \frac{w}{5}$. Redondee su respuesta a cuatro decimales.

56. [T] La transformación$T_{a,0} : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \space T_{a,0} (u,v) = (u + av, v)$, donde$a \neq 0$ es un número real, se llama cizallamiento en la$x$ dirección -dirección. La transformación$T_{b,0} : R^2 \rightarrow R^2, \space T_{o,b}(u,v) = (u,bu + v)$, donde$b \neq 0$ es un número real, se llama cizallamiento en la$y$ dirección -dirección.

a. Encontrar transformaciones$T_{0,2} \circ T_{3,0}$.

b. Encontrar la imagen$R$ de la región trapezoidal$S$ delimitada por$u = 0, \space v = 0, \space v = 1$, y$v = 2 - u$ a través de la transformación$T_{0,2} \circ T_{3,0}$.

c. Utilice un CAS para graficar la imagen$R$ en el$xy$ plano.

d. Encontrar el área de la región$R$ utilizando el área de la región$S$.

Contestar

a.$T_{0,2} \circ T_{3,0}(u,v) = (u + 3v, 2u + 7v)$;

b. La imagen$S$ es el cuadrilátero de vértices$(0,0), \space (3,7), \space (2,4)$, y$(4,9)$;

c.$S$ se grafica en la siguiente figura;

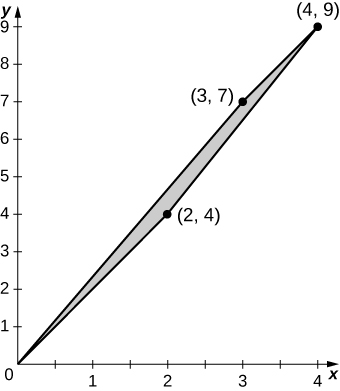
$Una figura de cuatro lados con puntos el origen, (2, 4), (4, 9) y (3, 7).$

Template:ContribOpenStaxCalc