16.4E: Ejercicios para la Sección 16.4

Para los siguientes ejercicios, evalúe las integrales de línea aplicando el teorema de Green.

1. \(\displaystyle \int_C 2xy\,dx+(x+y)\,dy\), donde\(C\) es el camino de\((0, 0)\) a\((1, 1)\) lo largo de la gráfica de\(y=x^3\) y de\((1, 1)\) a\((0, 0)\) lo largo de la gráfica de\(y=x\) orientado en el sentido contrario a las agujas del reloj

2. \(\displaystyle \int_C 2xy\,dx+(x+y)\,dy\), donde\(C\) está el límite de la región que se encuentra entre las gráficas de\(y=0\) y\(y=4−x^2\) orientado en sentido contrario a las agujas del reloj

Contestar

\(\displaystyle \int_C2xy\,dx+(x+y)\,dy=\frac{32}{3}\)unidades de trabajo

3. \(\displaystyle \int_C 2\arctan\left(\frac{y}{x}\right)\,dx+\ln(x^2+y^2)\,dy\), donde\(C\) se define por\(x=4+2\cos θ,\;y=4\sin θ\) orientado en el sentido contrario a las agujas del reloj

4. \(\displaystyle \int_C \sin x\cos y\,dx+(xy+\cos x\sin y)\,dy\), donde\(C\) está el límite de la región que se encuentra entre las gráficas de\(y=x\) y\(y=\sqrt{x}\) orientado en sentido contrario a las agujas del reloj

Contestar

\(\displaystyle \int_C\sin x\cos y\,dx+(xy+\cos x\sin y)\,dy=\frac{1}{12}\)unidades de trabajo

5. \(\displaystyle \int_C xy\,dx+(x+y)\,dy\), donde\(C\) está el límite de la región que se encuentra entre las gráficas de\(x^2+y^2=1\) y\(x^2+y^2=9\) orientado en sentido contrario a las agujas del reloj

6. \(\displaystyle ∮_C (−y\,dx+x\,dy)\), donde\(C\) consiste en un segmento\(C_1\) de línea de\((−1,0)\) a\((1, 0)\), seguido por el arco semicircular\(C_2\) de\((1, 0)\) vuelta a\((-1, 0)\)

Contestar

\(\displaystyle ∮_C (−y\,\,dx+x\,\,dy)=π\)unidades de trabajo

Para los siguientes ejercicios, use el teorema de Green.

7. Dejar\(C\) ser la curva que consiste en segmentos de línea de\((0, 0)\) a\((1, 1)\) a\((0, 1)\) y de vuelta a\((0, 0)\). Encuentra el valor de\(\displaystyle \int_C xy\,dx+\sqrt{y^2+1}\,dy\).

8. Evaluar integral de línea\(\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy\), donde\(C\) está el límite de la región entre círculos\(x^2+y^2=1\) y\(x^2+y^2=4\), y es una curva orientada positivamente.

Contestar

\(\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy=0\)unidades de trabajo

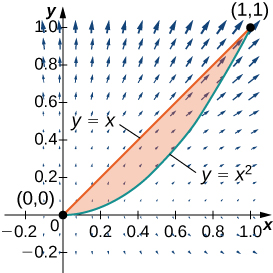
9. Encuentra la circulación de campo en sentido antihorario\(\vecs F(x,y)=xy\,\mathbf{\hat i}+y^2\,\mathbf{\hat j}\) alrededor y sobre el límite de la región encerrada por curvas\(y=x^2\) y\(y=x\) en el primer cuadrante y orientada en sentido antihorario.

10. Evaluar\(\displaystyle ∮_C y^3\,dx−x^3y^2\,dy\), donde\(C\) está el círculo de radio orientado positivamente\(2\) centrado en el origen.

Contestar

\(\displaystyle ∮_C y^3\,dx−x^3y^2\,dy=−20π\)unidades de trabajo

11. Evaluar\(\displaystyle ∮_C y^3\,dx−x^3\,dy\), donde\(C\) incluye los dos círculos de radio\(2\) y radio\(1\) centrados en el origen, ambos con orientación positiva.

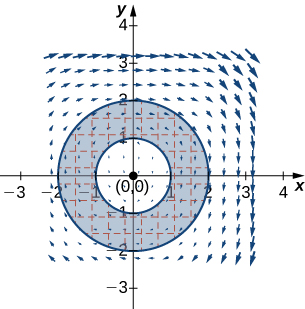
12. Calcular\(\displaystyle ∮_C −x^2y\,dx+xy^2\,dy\), donde\(C\) hay un círculo de radio\(2\) centrado en el origen y orientado en sentido contrario a las agujas del reloj.

Contestar

\(\displaystyle ∮_C −x^2y\,dx+xy^2\,dy=8π\)unidades de trabajo

13. Calcular integral\(\displaystyle ∮_C 2[y+x\sin(y)]\,dx+[x^2\cos(y)−3y^2]\,dy\) a lo largo del triángulo\(C\) con vértices\((0, 0), \,(1, 0)\) y\((1, 1)\), orientado en sentido antihorario, usando el teorema de Green.

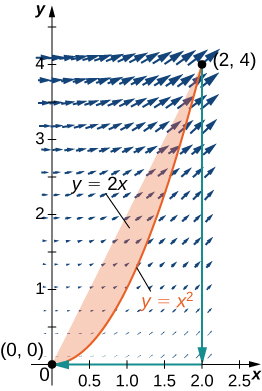
14. Evaluar integral\(\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy\), donde\(C\) está la curva que sigue\(y=x^2\) a la parábola desde\((0,0), \,(2,4),\) entonces la línea de\((2, 4)\) a\((2, 0)\), y finalmente la línea de\((2, 0)\) a\((0, 0)\).

Contestar

\(\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy=0\)unidades de trabajo

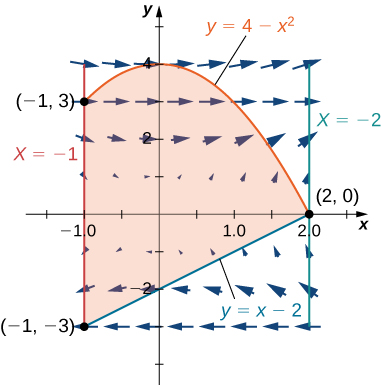
15. Evaluar la integral de línea\(\displaystyle ∮_C (y−\sin(y)\cos(y))\,dx+2x\sin^2(y)\,dy\), donde\(C\) se orienta en una trayectoria en sentido antihorario alrededor de la región delimitada por\(x=−1, \,x=2, \,y=4−x^2\), y\(y=x−2.\)

Para los siguientes ejercicios, usa el teorema de Green para encontrar el área.

16. Encuentra el área entre elipse\(\frac{x^2}{9}+\frac{y^2}{4}=1\) y círculo\(x^2+y^2=25\).

Contestar

\(A=19π\;\text{units}^2\)

17. Encontrar el área de la región encerrada por la ecuación paramétrica

\(\vecs p(θ)=(\cos(θ)−\cos^2(θ))\,\mathbf{\hat i}+(\sin(θ)−\cos(θ)\sin(θ))\,\mathbf{\hat j}\)para\(0≤θ≤2π.\)

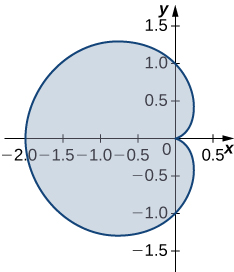
18. Encontrar el área de la región delimitada por hipocicloide\(\vecs r(t)=\cos^3(t)\,\mathbf{\hat i}+\sin^3(t)\,\mathbf{\hat j}\). La curva es parametrizada por\(t∈[0,2π].\)

Contestar

\(A=\frac{3}{8π}\;\text{units}^2\)

19. Encuentra el área de un pentágono con vértices\((0,4), \,(4,1), \,(3,0), \,(−1,−1),\) y\((−2,2)\).

20. Utilice el teorema de Green para evaluar\(\displaystyle \int_{C^+}(y^2+x^3)\,dx+x^4\,dy\), donde\(C^+\) está el perímetro del cuadrado\([0,1]×[0,1]\) orientado en sentido antihorario.

Contestar

\(\displaystyle \int_{C^+} (y^2+x^3)\,dx+x^4\,dy=0\)

21. Utilice el teorema de Green para probar el área de un disco con radio\(a\) es\(A=πa^2\;\text{units}^2\).

22. Usa el teorema de Green para encontrar el área de un bucle de una rosa de cuatro hojas\(r=3\sin 2θ\). (Pista:\(x\,dy−y\,dx=r^2\,dθ\)).

Contestar

\(A=\frac{9π}{8}\;\text{units}^2\)

23. Usa el teorema de Green para encontrar el área bajo un arco del cicloide dada por las ecuaciones paramétricas:\(x=t−\sin t,\;y=1−\cos t,\;t≥0.\)

24. Usa el teorema de Green para encontrar el área de la región encerrada por curva

\(\vecs r(t)=t^2\,\mathbf{\hat i}+\left(\frac{t^3}{3}−t\right)\,\mathbf{\hat j},\)para\(−\sqrt{3}≤t≤\sqrt{3}\).

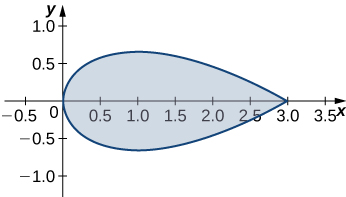
Contestar

\(A=\frac{8\sqrt{3}}{5}\;\text{units}^2\)

25. [T] Evaluar el teorema de Green utilizando un sistema de álgebra computacional para evaluar la integral\(\displaystyle \int_C xe^y\,dx+e^x\,dy\), donde\(C\) está el círculo dado por\(x^2+y^2=4\) y está orientado en sentido antihorario.

26. Evaluar\(\displaystyle \int_C(x^2y−2xy+y^2)\,ds\), donde\(C\) está el límite de la unidad cuadrada\(0≤x≤1,\;0≤y≤1\), atravesado en sentido antihorario.

Contestar

\(\displaystyle \int_C (x^2y−2xy+y^2)\,ds=3\)

27. Evaluar\(\displaystyle \int_C \frac{−(y+2)\,dx+(x−1)\,dy}{(x−1)^2+(y+2)^2}\), donde\(C\) está cualquier curva cerrada simple con un interior que no contenga puntos\((1,−2)\) atravesados en sentido antihorario.

28. Evaluar\(\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}\), donde\(C\) está cualquier curva cerrada simple, lisa, por tramos, que encierra el origen, atravesada en sentido antihorario.

Contestar

\(\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}=2π\)

Para los siguientes ejercicios, utilice el teorema de Green para calcular el trabajo realizado por la fuerza\(\vecs F\) sobre una partícula que se mueve en sentido antihorario alrededor de un camino cerrado\(C\).

29. \(\vecs F(x,y)=xy\,\mathbf{\hat i}+(x+y)\,\mathbf{\hat j}, \quad C:x^2+y^2=4\)

30. \(\vecs F(x,y)=(x^{3/2}−3y)\,\mathbf{\hat i}+(6x+5\sqrt{y})\,\mathbf{\hat j}, \quad C\): boundary of a triangle with vertices \((0, 0), \,(5, 0),\) and \((0, 5)\)

Answer

\(W=\frac{225}{2}\) units of work

31. Evaluate \(\displaystyle \int_C (2x^3−y^3)\,dx+(x^3+y^3)\,dy\), where \(C\) is a unit circle oriented in the counterclockwise direction.

32. A particle starts at point \((−2,0)\), moves along the \(x\)-axis to \((2, 0)\), and then travels along semicircle \(y=\sqrt{4−x^2}\) to the starting point. Use Green’s theorem to find the work done on this particle by force field \(\vecs F(x,y)=x\,\mathbf{\hat i}+(x^3+3xy^2)\,\mathbf{\hat j}\).

Answer

\(W=12π\) units of work

33. David and Sandra are skating on a frictionless pond in the wind. David skates on the inside, going along a circle of radius \(2\) in a counterclockwise direction. Sandra skates once around a circle of radius \(3\), also in the counterclockwise direction. Suppose the force of the wind at point \((x,y)\) is \(\vecs F(x,y)=(x^2y+10y)\,\mathbf{\hat i}+(x^3+2xy^2)\,\mathbf{\hat j}\). Use Green’s theorem to determine who does more work.

34. Use Green’s theorem to find the work done by force field \(\vecs F(x,y)=(3y−4x)\,\mathbf{\hat i}+(4x−y)\,\mathbf{\hat j}\) when an object moves once counterclockwise around ellipse \(4x^2+y^2=4.\)

Answer

\(W=2π\) units of work

35. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C e^{2x}\sin 2y\,dx+e^{2x}\cos 2y\,dy\), where \(C\) is ellipse \(9(x−1)^2+4(y−3)^2=36\) oriented counterclockwise.

36. Evaluate line integral \(\displaystyle ∮_C y^2\,dx+x^2\,dy\), where \(C\) is the boundary of a triangle with vertices \((0,0), \,(1,1)\), and \((1,0)\), with the counterclockwise orientation.

Answer

\(\displaystyle ∮_C y^2\,dx+x^2\,dy=\frac{1}{3}\) units of work

37. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C \vecs h·d\vecs r\) if \(\vecs h(x,y)=e^y\,\mathbf{\hat i}−\sin πx\,\mathbf{\hat j}\), where \(C\) is a triangle with vertices \((1, 0), \,(0, 1),\) and \((−1,0),\) traversed counterclockwise.

38. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C\sqrt{1+x^3}\,dx+2xy\,dy\) where \(C\) is a triangle with vertices \((0, 0), \,(1, 0),\) and \((1, 3)\) oriented clockwise.

Answer

\(\displaystyle \int_C \sqrt{1+x^3}\,dx+2xy\,dy=3\) units of work

39. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C x^2y\,dx−xy^2\,dy\) where \(C\) is a circle \(x^2+y^2=4\) oriented counterclockwise.

40. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy\) where \(C\) is circle \(x^2+y^2=9\) oriented in the counterclockwise direction.

Answer

\(\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy=36π\) units of work

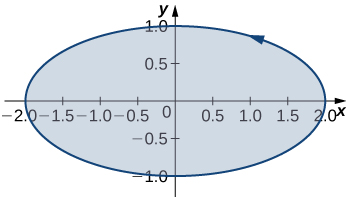
41. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C (3x−5y)\,dx+(x−6y)\,dy\), where \(C\) is ellipse \(\frac{x^2}{4}+y^2=1\) and is oriented in the counterclockwise direction.

42. Let \(C\) be a triangular closed curve from \((0, 0)\) to \((1, 0)\) to \((1, 1)\) and finally back to \((0, 0).\) Let \(\vecs F(x,y)=4y\,\mathbf{\hat i}+6x^2\,\mathbf{\hat j}.\) Use Green’s theorem to evaluate \(\displaystyle ∮_C\vecs F·d\vecs r.\)

Answer

\(\displaystyle ∮_C\vecs F·d\vecs r=2\) units of work

43. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C y\,dx−x\,dy\), where \(C\) is circle \(x^2+y^2=a^2\) oriented in the clockwise direction.

44. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy,\) where \(C\) is any smooth simple closed curve joining the origin to itself oriented in the counterclockwise direction.

Answer

\(\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy=0\) units of work

45. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C \left(y−\ln(x^2+y^2)\right)\,dx+\left(2\arctan \frac{y}{x}\right)\,dy,\) where \(C\) is the positively oriented circle \((x−2)^2+(y−3)^2=1.\)

46. Use Green’s theorem to evaluate \(\displaystyle ∮_C xy\,dx+x^3y^3\,dy,\) where \(C\) is a triangle with vertices \((0, 0), \,(1, 0),\) and \((1, 2)\) with positive orientation.

Answer

\(\displaystyle ∮_C xy\,dx+x^3y^3\,dy=2221\) units of work

47. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C \sin y\,dx+x\cos y\,dy,\) where \(C\) is ellipse \(x^2+xy+y^2=1\) oriented in the counterclockwise direction.

48. Let \(\vecs F(x,y)=\left(\cos(x^5)−13y^3\right)\,\mathbf{\hat i}+13x^3\,\mathbf{\hat j}.\) Find the counterclockwise circulation \(\displaystyle ∮_C\vecs F·d\vecs r,\) where \(C\) is a curve consisting of the line segment joining \((−2,0)\) and \((−1,0),\) half circle \(y=\sqrt{1−x^2},\) the line segment joining \((1, 0)\) and \((2, 0),\) and half circle \(y=\sqrt{4−x^2}.\)

Answer

\(\displaystyle ∮_C\vecs F·d\vecs r=15π^4\) units of work

49. Use Green’s theorem to evaluate line integral \(\displaystyle ∫_C \sin(x^3)\,dx+2ye^{x^2}\,dy,\) where \(C\) is a triangular closed curve that connects the points \((0, 0), \,(2, 2),\) and \((0, 2)\) counterclockwise.

50. Let \(C\) be the boundary of square \(0≤x≤π,\;0≤y≤π,\) traversed counterclockwise. Use Green’s theorem to find \(\displaystyle ∫_C \sin(x+y)\,dx+\cos(x+y)\,dy.\)

Answer

\(\displaystyle \int_C\sin(x+y)\,dx+\cos(x+y)\,dy=4\) units of work

51. Use Green’s theorem to evaluate line integral \(\displaystyle ∫_C \vecs F·d\vecs r,\) where \(\vecs F(x,y)=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},\) and \(C\) is a triangle bounded by \(y=0,\;x=3,\) and \(y=x,\) oriented counterclockwise.

52. Use Green’s Theorem to evaluate integral \(\displaystyle ∫_C \vecs F·d\vecs r,\) where \(\vecs F(x,y)=(xy^2)\,\mathbf{\hat i}+x\,\mathbf{\hat j},\) and \(C\) is a unit circle oriented in the counterclockwise direction.

Answer

\(\displaystyle ∫_C \vecs F·d\vecs r=π\) units of work

53. Use Green’s theorem in a plane to evaluate line integral \(\displaystyle ∮_C (xy+y^2)\,dx+x^2\,dy,\) where \(C\) is a closed curve of a region bounded by \(y=x\) and \(y=x^2\) oriented in the counterclockwise direction.

54. Calculate the outward flux of \(\vecs F(x,y)=−x\,\mathbf{\hat i}+2y\,\mathbf{\hat j}\) over a square with corners \((±1,\,±1),\) where the unit normal is outward pointing and oriented in the counterclockwise direction.

Answer

\(\displaystyle ∮_C\vecs F·\vecs N \,ds=4\)

55. [T] Let \(C\) be circle \(x^2+y^2=4\) oriented in the counterclockwise direction. Evaluate \(\displaystyle ∮_C \left[\left(3y−e^{\arctan x})\,dx+(7x+\sqrt{y^4+1}\right)\,dy\right]\) using a computer algebra system.

56. Find the flux of field \(\vecs F(x,y)=−x\,\mathbf{\hat i}+y\,\mathbf{\hat j}\) across \(x^2+y^2=16\) oriented in the counterclockwise direction.

Answer

\(\displaystyle ∮_C \vecs F·\vecs N\,ds=32π\)

57. Let \(\vecs F=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},\) and let \(C\) be a triangle bounded by \(y=0, \,x=3,\) and \(y=x\) oriented in the counterclockwise direction. Find the outward flux of \(\vecs F\) through \(C\).

58. [T] Let \(C\) be unit circle \(x^2+y^2=1\) traversed once counterclockwise. Evaluate \(\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy\) by using a computer algebra system.

Answer

\(\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy=4.7124\) units of work

59. [T] Find the outward flux of vector field \(\vecs F(x,y)=xy^2\,\mathbf{\hat i}+x^2y\,\mathbf{\hat j}\) across the boundary of annulus \(R=\big\{(x,y):1≤x^2+y^2≤4\big\}=\big\{(r,θ):1≤r≤2,\,0≤θ≤2π\big\}\) using a computer algebra system.

60. Consider region \(R\) bounded by parabolas \(y=x^2\) and \(x=y^2.\) Let \(C\) be the boundary of \(R\) oriented counterclockwise. Use Green’s theorem to evaluate \(\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy.\)

Answer

\(\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy=13\) units of work

Contributors

Template:contribopenstaxcalc