16.8: El teorema de la divergencia

Objetivos de aprendizaje

• Explicar el significado del teorema de la divergencia.
• Utilice el teorema de divergencia para calcular el flujo de un campo vectorial.
• Aplicar el teorema de divergencia a un campo electrostático.

Hemos examinado varias versiones del Teorema Fundamental del Cálculo en dimensiones superiores que relacionan la integral alrededor de un límite orientado de un dominio con una “derivada” de esa entidad en el dominio orientado. En esta sección, exponemos el teorema de la divergencia, que es el teorema final de este tipo que vamos a estudiar. El teorema de divergencia tiene muchos usos en física; en particular, el teorema de divergencia se utiliza en el campo de las ecuaciones diferenciales parciales para derivar ecuaciones que modelan el flujo de calor y la conservación de la masa. Utilizamos el teorema para calcular integrales de flujo y aplicarlo a campos electrostáticos.

Descripción general de los teoremas

Antes de examinar el teorema de la divergencia, es útil comenzar con una visión general de las versiones del Teorema Fundamental del Cálculo que hemos discutido:

1. El Teorema Fundamental del Cálculo:\[\int_a^b f' (x) \, dx = f(b) - f(a). \nonumber \] Este teorema relaciona la integral del segmento derivado\(f'\) sobre línea a\([a,b]\) lo largo del\(x\) eje -eje con una diferencia de\(f\) evaluado en el límite.
2. El Teorema Fundamental para Integrales de Línea:\[\int_C \vecs \nabla f \cdot d\vecs r = f(P_1) - f(P_0), \nonumber \] donde\(P_0\) es el punto inicial de\(C\) y\(P_1\) es el punto terminal de\(C\). El Teorema Fundamental para Integrales de Línea permite\(C\) que la ruta sea una ruta en un plano o en el espacio, no solo un segmento de línea en el\(x\) eje. Si pensamos en el gradiente como una derivada, entonces este teorema relaciona una integral de derivada\(\nabla f\) sobre camino\(C\) a una diferencia de\(f\) evaluado en el límite de\(C\).
3. Teorema de Green, forma de circulación:\[\iint_D (Q_x - P_y)\,dA = \int_C \vecs F \cdot d\vecs r. \nonumber \] Dado que\(Q_x - P_y = \text{curl } \vecs F \cdot \mathbf{\hat k}\) y curl es una especie derivada, El teorema de Green relaciona la integral del rizo derivado\(\vecs F\) sobre la región plana\(D\) con una integral de\(\vecs F\) sobre el límite de\(D\).
4. Teorema de Green, forma de flujo:\[\iint_D (P_x + Q_y)\,dA = \int_C \vecs F \cdot \vecs N \, dS. \nonumber \] Dado que\(P_x + Q_y = \text{div }\vecs F\) y la divergencia es una especie derivada, la forma de flujo del teorema de Green relaciona la integral de div derivada\(\vecs F\) sobre la región plana\(D\) con una integral de\(\vecs F\) sobre el límite de\(D\).
5. Teorema de Stokes:\[\iint_S curl \, \vecs F \cdot d\vecs S = \int_C \vecs F \cdot d\vecs r. \nonumber \] Si pensamos en el rizo como una especie de derivado, entonces el teorema de Stokes relaciona la integral del rizo derivado\(\vecs F\) sobre la superficie\(S\) (no necesariamente plana) con una integral de\(\vecs F\) sobre el límite de\(S\).

Declarando el Teorema de la Divergencia

El teorema de la divergencia sigue el patrón general de estos otros teoremas. Si pensamos en la divergencia como una especie de derivada, entonces el teorema de divergencia relaciona una triple integral de div derivada\(\vecs F\) sobre un sólido a una integral de flujo de\(\vecs F\) sobre el límite del sólido. Más específicamente, el teorema de divergencia relaciona una integral de flujo del campo vectorial\(\vecs F\) sobre una superficie cerrada\(S\) con una triple integral de la divergencia de\(\vecs F\) sobre el sólido encerrado por\(S\).

El teorema de la divergencia

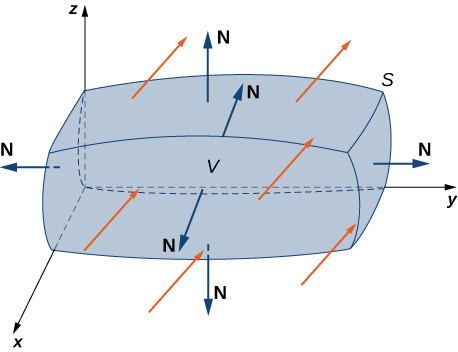
Deje\(S\) ser una superficie cerrada lisa y por partes que encierra sólidos\(E\) en el espacio. Supongamos que\(S\) está orientado hacia afuera, y deja\(\vecs F\) ser un campo vectorial con derivadas parciales continuas sobre una región abierta que contiene\(E\) (Figura\(\PageIndex{1}\)). Entonces

\[\iiint_E \text{div }\vecs F \, dV = \iint_S \vecs F \cdot d\vecs S. \label{divtheorem} \]

Figura\(\PageIndex{1}\): El teorema de divergencia relaciona una integral de flujo\(S\) a través de una superficie cerrada con una triple integral sobre un sólido\(E\) encerrado por la superficie.

Recordemos que la forma de flujo del teorema de Green afirma que

\[ \iint_D \text{div }\vecs F \, dA = \int_C \vecs F \cdot \vecs N \, dS. \nonumber \]

Por lo tanto, el teorema de la divergencia es una versión del teorema de Green en una dimensión superior.

La prueba del teorema de la divergencia está fuera del alcance de este texto. No obstante, nos fijamos en una prueba informal que da una idea general de por qué el teorema es cierto, pero no prueba el teorema con pleno rigor. Esta explicación sigue la explicación informal dada de por qué el teorema de Stokes es cierto.

Prueba

Dejar\(B\) ser una pequeña caja con lados paralelos a los planos de coordenadas en su interior\(E\) (Figura\(\PageIndex{2a}\)). Deje que el centro de\(B\) tenga coordenadas\((x,y,z)\) y supongamos que las longitudes de borde son\(\Delta x, \, \Delta y\), y\(\Delta z\). (Figura\(\PageIndex{1b}\)). El vector normal fuera de la parte superior de la caja es\(\mathbf{\hat k}\) y el vector normal fuera de la parte inferior de la caja es\(-\mathbf{\hat k}\). El producto punto de\(\vecs F = \langle P, Q, R \rangle\) con\(\mathbf{\hat k}\) es\(R\) y el producto punto con\(-\mathbf{\hat k}\) es\(-R\). El área de la parte superior de la caja (y la parte inferior de la caja)\(\Delta S\) es\(\Delta x \Delta y\).

Figura\(\PageIndex{2}\): (a) Una pequeña superficie\(B\) interior de caja\(E\) tiene lados paralelos a los planos de coordenadas. (b)\(B\) La caja tiene longitudes laterales\(\Delta x, \, \Delta y\), y\(\Delta z\) (c) Si miramos la vista lateral de\(B\), vemos que, ya que\((x,y,z)\) es el centro de la caja, para llegar a la parte superior de la caja debemos recorrer una distancia vertical de\(\Delta z\) hacia arriba desde\((x,y,z)\). De igual manera, para llegar al fondo de la caja debemos recorrer una distancia\(\Delta z\) hacia abajo desde\((x,y,z)\).

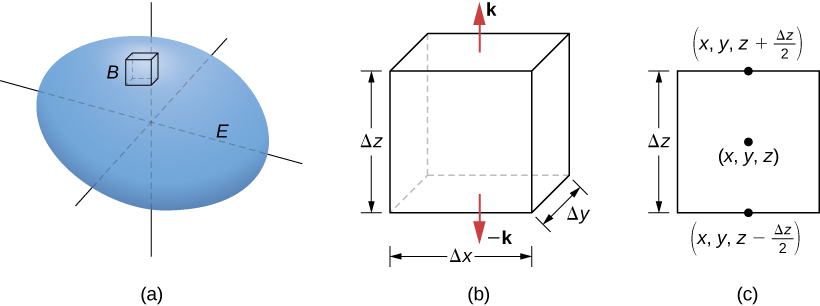
El flujo que sale de la parte superior de la caja se puede aproximar por\(R \left(x,\, y,\, z + \frac{\Delta z}{2}\right) \,\Delta x \,\Delta y\) (Figura\(\PageIndex{2c}\)) y el flujo que sale de la parte inferior de la caja es\(- R \left(x,\, y,\, z - \frac{\Delta z}{2}\right) \,\Delta x \,\Delta y\). Si denotamos la diferencia entre estos valores como\(\Delta R\), entonces el flujo neto en la dirección vertical se puede aproximar por\(\Delta R\, \Delta x \,\Delta y\). Sin embargo,

\[\Delta R \,\Delta x \,\Delta y = \left(\frac{\Delta R}{\Delta z}\right) \,\Delta x \,\Delta y \Delta z \approx \left(\frac{\partial R}{\partial z}\right) \,\Delta V.\nonumber \]

Por lo tanto, el flujo neto en la dirección vertical se puede aproximar por\(\left(\frac{\partial R}{\partial z}\right)\Delta V\). De manera similar, el flujo neto en la\(x\) dirección -se puede aproximar por\(\left(\frac{\partial P}{\partial x}\right)\,\Delta V\) y el flujo neto en la\(y\) dirección se puede aproximar por\(\left(\frac{\partial Q}{\partial y}\right)\,\Delta V\). La adición de los flujos en las tres direcciones da una aproximación del flujo total fuera de la caja:

\[\text{Total flux }\approx \left(\frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \right) \Delta V = \text{div }\vecs F \,\Delta V. \nonumber \]

Esta aproximación se aproxima arbitrariamente al valor del flujo total a medida que el volumen de la caja se contrae a cero.

La suma de\(\text{div }\vecs F \,\Delta V\) sobre todas las cajas pequeñas aproximándose\(E\) es aproximadamente\(\iiint_E \text{div }\vecs F \,dV\). Por otro lado, la suma de\(\text{div }\vecs F \,\Delta V\) sobre todas las cajas pequeñas que\(E\) se aproximan es la suma de los fundentes sobre todas estas cajas. Al igual que en la prueba informal del teorema de Stokes, sumar estos flujos sobre todas las casillas da como resultado la cancelación de gran parte de los términos. Si una caja de aproximación comparte una cara con otra caja de aproximación, entonces el flujo sobre una cara es el negativo del flujo sobre la cara compartida de la caja adyacente. Estas dos integrales se cancelan. Al sumar todos los flujos, las únicas integrales de flujo que sobreviven son las integrales sobre las caras que se aproximan al límite de\(E\). A medida que los volúmenes de las cajas aproximadas se reducen a cero, esta aproximación se aproxima arbitrariamente al flujo sobre\(S\).

\(\Box\)

Ejemplo\(\PageIndex{1}\): Verifying the Divergence Theorem

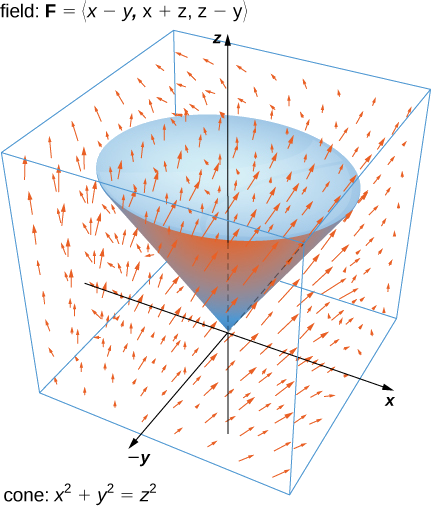
Verificar el teorema de divergencia para el campo vectorial\(\vecs F = \langle x - y, \, x + z, \, z - y \rangle\) y la superficie\(S\) que consiste en cono\(x^2 + y^2 = z^2, \, 0 \leq z \leq 1\), y la parte superior circular del cono (ver la siguiente figura). Supongamos que esta superficie está orientada positivamente.

Solución

Let\(E\) be the solid cone enclosed by \(S\). To verify the theorem for this example, we show that

\[\iiint_E \text{div } \vecs F \,dV = \iint_S \vecs F \cdot d\vecs S\nonumber \]

by calculating each integral separately.

To compute the triple integral, note that \(\text{div } \vecs F = P_x + Q_y + R_z = 2\), and therefore the triple integral is

\[ \begin{align*} \iiint_E \text{div } \vecs F \, dV &= 2 \iiint_E dV \\[4pt] &= 2 \, (volume \, of \, E). \end{align*}\]

The volume of a right circular cone is given by \(\pi r^2 \frac{h}{3}\). In this case, \(h = r = 1\). Therefore,

\[\iiint_E \text{div } \vecs F \,dV = 2 \, (volume \, of \, E) = \frac{2\pi}{3}.\nonumber \]

To compute the flux integral, first note that \(S\) is piecewise smooth; \(S\) can be written as a union of smooth surfaces. Therefore, we break the flux integral into two pieces: one flux integral across the circular top of the cone and one flux integral across the remaining portion of the cone. Call the circular top \(S_1\) and the portion under the top \(S_2\). We start by calculating the flux across the circular top of the cone. Notice that \(S_1\) has parameterization

\[\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, 1 \rangle, \, 0 \leq u \leq 1, \, 0 \leq v \leq 2\pi.\nonumber \]

Then, the tangent vectors are \(\vecs t_u = \langle \cos v, \, \sin v, \, 0 \rangle \) and \(\vecs t_v = \langle -u \, \sin v, \, u \, \cos v, 0 \rangle \). Therefore, the flux across \(S_1\) is

\[ \begin{align*} \iint_{S_1} \vecs F \cdot d\vecs S &= \int_0^1 \int_0^{2\pi} \vecs F (\vecs r ( u,v)) \cdot (\vecs t_u \times \vecs t_v) \, dA \\[4pt] &= \int_0^1 \int_0^{2\pi} \langle u \, \cos v - u \, \sin v, \, u \, \cos v + 1, \, 1 - u \, \sin v \rangle \cdot \langle 0,0,u \rangle \, dv\, du \\[4pt] &= \int_0^1 \int_0^{2\pi} u - u^2 \sin v \, dv du \\[4pt] &= \pi. \end{align*}\]

We now calculate the flux over \(S_2\). A parameterization of this surface is

\[\vecs r(u,v) = \langle u \, \cos v, \, u \, \sin v, \, u \rangle, \, 0 \leq u \leq 1, \, 0 \leq v \leq 2\pi.\nonumber \]

The tangent vectors are \(\vecs t_u = \langle \cos v, \, \sin v, \, 1 \rangle \) and \(\vecs t_v = \langle -u \, \sin v, \, u \, \cos v, 0 \rangle \), so the cross product is

\[\vecs t_u \times \vecs t_v = \langle - u \, \cos v, \, -u \, \sin v, \, u \rangle.\nonumber \]

Notice that the negative signs on the \(x\) and \(y\) components induce the negative (or inward) orientation of the cone. Since the surface is positively oriented, we use vector \(\vecs t_v \times \vecs t_u = \langle u \, \cos v, \, u \, \sin v, \, -u \rangle\) in the flux integral. The flux across \(S_2\) is then

\[ \begin{align*} \iint_{S_2} \vecs F \cdot d\vecs S &= \int_0^1 \int_0^{2\pi} \vecs F ( \vecs r ( u,v)) \cdot (\vecs t_u \times \vecs t_v) \, dA \\[4pt] &= \int_0^1 \int_0^{2\pi} \langle u \, \cos v - u \, \sin v, \, u \, \cos v + u, \, u \, - u\sin v \rangle \cdot \langle u \, \cos v, \, u \, \sin v, \, -u \rangle\,dv\,du \\[4pt] &= \int_0^1 \int_0^{2\pi} u^2 \cos^2 v + 2u^2 \sin v - u^2 \,dv\,du \\[4pt] &= -\frac{\pi}{3} \end{align*}\]

The total flux across \(S\) is

\[\iint_{S} \vecs F \cdot d\vecs S = \iint_{S_1}\vecs F \cdot d\vecs S + \iint_{S_2} \vecs F \cdot d\vecs S = \frac{2\pi}{3} = \iiint_E \text{div } \vecs F \,dV,\nonumber \]

and we have verified the divergence theorem for this example.

Exercise \(\PageIndex{1}\)

Verify the divergence theorem for vector field \(\vecs F (x,y,z) = \langle x + y + z, \, y, \, 2x - y \rangle\) and surface \(S\) given by the cylinder \(x^2 + y^2 = 1, \, 0 \leq z \leq 3\) plus the circular top and bottom of the cylinder. Assume that \(S\) is positively oriented.

Hint

Calculate both the flux integral and the triple integral with the divergence theorem and verify they are equal.

Answer

Both integrals equal \(6\pi\).

​​Recall that the divergence of continuous field \(\vecs F\) at point \(P\) is a measure of the “outflowing-ness” of the field at \(P\). If \(\vecs F\) represents the velocity field of a fluid, then the divergence can be thought of as the rate per unit volume of the fluid flowing out less the rate per unit volume flowing in. The divergence theorem confirms this interpretation. To see this, let \(P\) be a point and let \(B_{\tau}\) be a ball of small radius \(r\) centered at \(P\) (Figure \(\PageIndex{3}\)). Let \(S_{\tau}\) be the boundary sphere of \(B_{\tau}\). Since the radius is small and \(\vecs F\) is continuous, \(\text{div }\vecs F(Q) \approx \text{div }\vecs F(P)\) for all other points \(Q\) in the ball. Therefore, the flux across \(S_{\tau}\) can be approximated using the divergence theorem:

\[\iint_{S_{\tau}} \vecs F \cdot d\vecs S = \iiint_{B_{\tau}} \text{div }\vecs F \,dV \approx \iiint_{B_{\tau}} \text{div }\vecs F(P) \,dV.\nonumber \]

Since \( div F(P)\) is a constant,

\[\iiint_{B_{\tau}} \text{div }\vecs F(P) \,dV = \text{div }\vecs F(P) \, V(B_{\tau}).\nonumber \]

Therefore, flux \[\iint_{S_{\tau}} \vecs F \cdot d\vecs S \nonumber \] can be approximated by \(\vecs F(P) \, V(B_{\tau})\). This approximation gets better as the radius shrinks to zero, and therefore

\[\text{div } \vecs F(P) = \lim_{\tau \rightarrow 0} \frac{1}{V(B_{\tau})} \iint_{S_{\tau}} \vecs F \cdot d\vecs S.\nonumber \]

This equation says that the divergence at \(P\) is the net rate of outward flux of the fluid per unit volume.

Figure \(\PageIndex{3}\): Ball \(B_{\tau}\) of small radius \(r\) centered at \(P\).

Using the Divergence Theorem

The divergence theorem translates between the flux integral of closed surface \(S\) and a triple integral over the solid enclosed by \(S\). Therefore, the theorem allows us to compute flux integrals or triple integrals that would ordinarily be difficult to compute by translating the flux integral into a triple integral and vice versa.

Example \(\PageIndex{2}\): Applying the Divergence Theorem

Calculate the surface integral

\[\iint_S \vecs F \cdot d\vecs S, \nonumber \]

where \(S\) is cylinder \(x^2 + y^2 = 1, \, 0 \leq z \leq 2\), including the circular top and bottom, and \(\vecs F = \left\langle \frac{x^3}{3} + yz, \, \frac{y^3}{3} - \sin (xz), \, z - x - y \right\rangle\).

Solution

We could calculate this integral without the divergence theorem, but the calculation is not straightforward because we would have to break the flux integral into three separate integrals: one for the top of the cylinder, one for the bottom, and one for the side. Furthermore, each integral would require parameterizing the corresponding surface, calculating tangent vectors and their cross product..

By contrast, the divergence theorem allows us to calculate the single triple integral

\[\iiint_E \text{div }\vecs F \, dV,\nonumber \]

where \(E\) is the solid enclosed by the cylinder. Using the divergence theorem (Equation \ref{divtheorem}) and converting to cylindrical coordinates, we have

\[ \begin{align*} \iint_S \vecs F \cdot d\vecs S &= \iiint_E \text{div }\vecs F \, dV, \\[4pt]
&= \iiint_E (x^2 + y^2 + 1) \, dV \\[4pt]
&= \int_0^{2\pi} \int_0^1 \int_0^2 (r^2 + 1) \, r \, dz \, dr \, d\theta \\[4pt]
&= \frac{3}{2} \int_0^{2\pi} d\theta \\[4pt]
&= 3\pi. \end{align*}\]

Exercise \(\PageIndex{2}\)

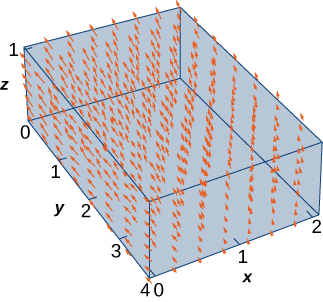
Use the divergence theorem to calculate flux integral \[\iint_S \vecs F \cdot d\vecs S,\nonumber \] where \(S\) is the boundary of the box given by \(0 \leq x \leq 2, \, 0 \leq y \leq 4, \, 0 \leq z \leq 1\) and \(\vecs F = \langle x^2 + yz, \, y - z, \, 2x + 2y + 2z \rangle \) (see the following figure).

Pista

Calcular la triple integral correspondiente.

Contestar

40

Ejemplo\(\PageIndex{3}\): Applying the Divergence Theorem

Dejar\(\vecs v = \left\langle - \frac{y}{z}, \, \frac{x}{z}, \, 0 \right\rangle\) ser el campo de velocidad de un fluido. Dejar\(C\) ser el cubo sólido dado por\(1 \leq x \leq 4, \, 2 \leq y \leq 5, \, 1 \leq z \leq 4\), y dejar\(S\) ser el límite de este cubo (ver la siguiente figura). Encuentre la velocidad de flujo del fluido a través\(S\).

Figura\(\PageIndex{4}\): Campo vectorial\(\vecs v = \left\langle - \frac{y}{z}, \, \frac{x}{z}, \, 0 \right\rangle\).

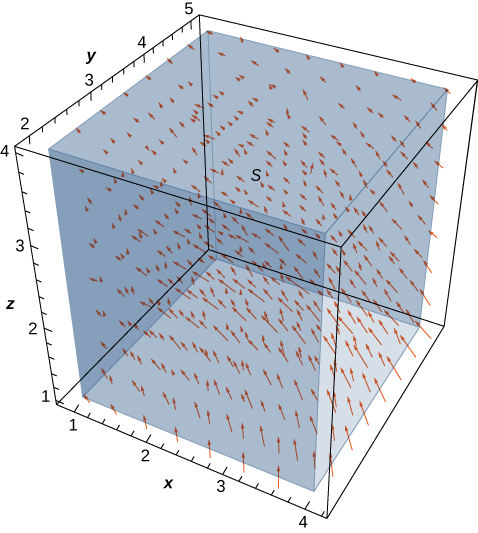
Solución

El caudal del fluido a través\(S\) es\(\iint_S \vecs v \cdot d\vecs S\). Antes de calcular esta integral de flujo, discutamos cuál debería ser el valor de la integral. Con base en la Figura\(\PageIndex{4}\), vemos que si colocamos este cubo en el fluido (siempre y cuando el cubo no abarque el origen), entonces la velocidad de fluido que ingresa al cubo es la misma que la velocidad de fluido que sale del cubo. El campo es de naturaleza rotacional y, para un círculo dado paralelo al\(xy\) plano -plano que tiene un centro en el eje z, los vectores a lo largo de ese círculo son todos de la misma magnitud. Es así como podemos ver que el caudal es el mismo entrando y saliendo del cubo. El flujo hacia el cubo se cancela con el flujo que sale del cubo y, por lo tanto, el caudal del fluido a través del cubo debe ser cero.

Para verificar esta intuición, necesitamos calcular la integral de flujo. Calcular la integral de flujo directamente requiere dividir la integral de flujo en seis integrales de flujo separadas, una para cada cara del cubo. También necesitamos encontrar vectores tangentes, computar su producto cruzado. Sin embargo, el uso del teorema de la divergencia hace que este cálculo vaya mucho más rápido:

\ [\ begin {align*}\ Iint_s\ vecs v\ cdot d\ vecs S &=\ IIint_c\ texto {div}\ vecs v\, dV\\ [4pt]
&=\ IIint_c 0\, dV = 0. \ end {alinear*}\]

Por lo tanto, el flujo es cero, como se esperaba.

Ejercicio\(\PageIndex{3}\)

Dejar\(\vecs v = \left\langle \frac{x}{z}, \, \frac{y}{z}, \, 0 \right\rangle\) ser el campo de velocidad de un fluido. Dejar\(C\) ser el cubo sólido dado por\(1 \leq x \leq 4, \, 2 \leq y \leq 5, \, 1 \leq z \leq 4\), y dejar\(S\) ser el límite de este cubo (ver la siguiente figura). Encuentre la velocidad de flujo del fluido a través\(S\).

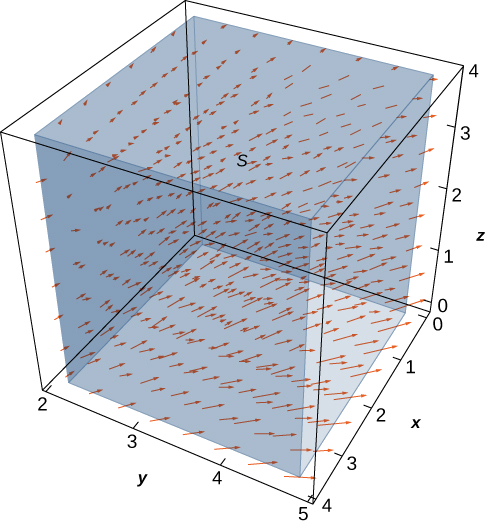
Pista

Usar el teorema de divergencia y calcular una triple integral

Contestar

\(9 \, \ln (16)\)

Example illustrates a remarkable consequence of the divergence theorem. Let \(S\) be a piecewise, smooth closed surface and let \(\vecs F\) be a vector field defined on an open region containing the surface enclosed by \(S\). If \(\vecs F\) has the form \(F = \langle f (y,z), \, g(x,z), \, h(x,y)\rangle\), then the divergence of \(\vecs F\) is zero. By the divergence theorem, the flux of \(\vecs F\) across \(S\) is also zero. This makes certain flux integrals incredibly easy to calculate. For example, suppose we wanted to calculate the flux integral \(\iint_S \vecs F \cdot d\vecs S\) where \(S\) is a cube and

\[\vecs F = \langle \sin (y) \, e^{yz}, \, x^2z^2, \, \cos (xy) \, e^{\sin x} \rangle. \nonumber \]

Calculating the flux integral directly would be difficult, if not impossible, using techniques we studied previously. At the very least, we would have to break the flux integral into six integrals, one for each face of the cube. But, because the divergence of this field is zero, the divergence theorem immediately shows that the flux integral is zero.

We can now use the divergence theorem to justify the physical interpretation of divergence that we discussed earlier. Recall that if \(\vecs F\) is a continuous three-dimensional vector field and \(P\) is a point in the domain of \(\vecs F\), then the divergence of \(\vecs F\) at \(P\) is a measure of the “outflowing-ness” of \(\vecs F\) at \(P\). If \(\vecs F\) represents the velocity field of a fluid, then the divergence of \(\vecs F\) at \(P\) is a measure of the net flow rate out of point \(P\) (the flow of fluid out of \(P\) less the flow of fluid in to \(P\)). To see how the divergence theorem justifies this interpretation, let \(B_{\tau}\) be a ball of very small radius r with center \(P\), and assume that \(B_{\tau}\) is in the domain of \(\vecs F\). Furthermore, assume that \(B_{\tau}\) has a positive, outward orientation. Since the radius of \(B_{\tau}\) is small and \(\vecs F\) is continuous, the divergence of \(\vecs F\) is approximately constant on \(B_{\tau}\). That is, ifv \(P'\) is any point in \(B_{\tau}\), then \(\text{div } \vecs F(P) \approx \text{div } \vecs F(P')\). Let \(S_{\tau}\) denote the boundary sphere of \(B_{\tau}\). We can approximate the flux across \(S_{\tau}\) using the divergence theorem as follows:

\[\begin{align*} \iint_{S_{\tau}} \vecs F \cdot d\vecs S &= \iiint_{B_{\tau}} \text{div }\vecs F \, dV \\[4pt]
&\approx \iiint_{B_{\tau}} \text{div } \vecs F (P) \, dV \\[4pt]
&= \text{div } \vecs F (P) \, V(B_{\tau}). \end{align*}\]

As we shrink the radius \(r\) to zero via a limit, the quantity \(\text{div }\vecs F (P) \, V(B_{\tau})\) gets arbitrarily close to the flux. Therefore,

\[\text{div }\vecs F(P) = \lim_{\tau \rightarrow 0} \frac{1}{V(B_{\tau})} \iint_{S_{\tau}} \vecs F \cdot d\vecs S \nonumber \]

and we can consider the divergence at \(P\) as measuring the net rate of outward flux per unit volume at \(P\). Since “outflowing-ness” is an informal term for the net rate of outward flux per unit volume, we have justified the physical interpretation of divergence we discussed earlier, and we have used the divergence theorem to give this justification.

Application to Electrostatic Fields

The divergence theorem has many applications in physics and engineering. It allows us to write many physical laws in both an integral form and a differential form (in much the same way that Stokes’ theorem allowed us to translate between an integral and differential form of Faraday’s law). Areas of study such as fluid dynamics, electromagnetism, and quantum mechanics have equations that describe the conservation of mass, momentum, or energy, and the divergence theorem allows us to give these equations in both integral and differential forms.

One of the most common applications of the divergence theorem is to electrostatic fields. An important result in this subject is Gauss’ law. This law states that if \(S\) is a closed surface in electrostatic field \(\vecs E\), then the flux of \(\vecs E\) across \(S\) is the total charge enclosed by \(S\) (divided by an electric constant). We now use the divergence theorem to justify the special case of this law in which the electrostatic field is generated by a stationary point charge at the origin.

If \((x,y,z)\) is a point in space, then the distance from the point to the origin is \(r = \sqrt{x^2 + y^2 + z^2}\). Let \(\vecs F_{\tau}\) denote radial vector field \(\vecs F_{\tau} = \dfrac{1}{\tau^2} \left\langle \dfrac{x}{\tau}, \, \dfrac{y}{\tau}, \, \dfrac{z}{\tau}\right\rangle \).The vector at a given position in space points in the direction of unit radial vector \(\left\langle \dfrac{x}{\tau}, \, \dfrac{y}{\tau}, \, \dfrac{z}{\tau}\right\rangle \) and is scaled by the quantity \(1/\tau^2\). Therefore, the magnitude of a vector at a given point is inversely proportional to the square of the vector’s distance from the origin. Suppose we have a stationary charge of \(q\) Coulombs at the origin, existing in a vacuum. The charge generates electrostatic field \(\vecs E\) given by

\[\vecs E = \dfrac{q}{4\pi \epsilon_0}\vecs F_{\tau}, \nonumber \]

where the approximation \(\epsilon_0 = 8.854 \times 10^{-12}\) farad (F)/m is an electric constant. (The constant \(\epsilon_0\) is a measure of the resistance encountered when forming an electric field in a vacuum.) Notice that \(\vecs E\) is a radial vector field similar to the gravitational field described in [link]. The difference is that this field points outward whereas the gravitational field points inward. Because

\[\vecs E = \dfrac{q}{4\pi \epsilon_0}\vecs F_{\tau} = \dfrac{q}{4\pi \epsilon_0}\left(\dfrac{1}{\tau^2} \left\langle \dfrac{x}{\tau}, \, \dfrac{y}{\tau}, \, \dfrac{z}{\tau}\right\rangle\right), \nonumber \]

we say that electrostatic fields obey an inverse-square law. That is, the electrostatic force at a given point is inversely proportional to the square of the distance from the source of the charge (which in this case is at the origin). Given this vector field, we show that the flux across closed surface \(S\) is zero if the charge is outside of \(S\), and that the flux is \(q/epsilon_0\) if the charge is inside of \(S\). In other words, the flux across S is the charge inside the surface divided by constant \(\epsilon_0\). This is a special case of Gauss’ law, and here we use the divergence theorem to justify this special case.

To show that the flux across \(S\) is the charge inside the surface divided by constant \(\epsilon_0\), we need two intermediate steps. First we show that the divergence of \(\vecs F_{\tau}\) is zero and then we show that the flux of \(\vecs F_{\tau}\) across any smooth surface \(S\) is either zero or \(4\pi\). We can then justify this special case of Gauss’ law.

Example \(\PageIndex{4}\): The Divergence of \(F_{\tau}\) is Zero

Verify that the divergence of \(\vecs F_{\tau}\) is zero where \(\vecs F_{\tau}\) is defined (away from the origin).

Solution

Since \(\tau = \sqrt{x^2 + y^2 + z^2}\), the quotient rule gives us

\[ \begin{align*} \dfrac{\partial}{\partial x} \left( \dfrac{x}{\tau^3} \right) &= \dfrac{\partial}{\partial x} \left( \dfrac{x}{(x^2+y^2+z^2)^{3/2}} \right) \\[4pt]
&= \dfrac{(x^2+y^2+z^2)^{3/2} - x\left[\dfrac{3}{2} (x^2+y^2+z^2)^{1/2}2x\right]}{(x^2+y^2+z^2)^3} \\[4pt]
&= \dfrac{\tau^3 -3x^2\tau}{\tau^6} = \dfrac{\tau^2 - 3x^2}{\tau^5}. \end{align*}\]

Similarly,

\[\dfrac{\partial}{\partial y} \left( \dfrac{y}{\tau^3} \right) = \dfrac{\tau^2 - 3y^2}{\tau^5} \, and \, \dfrac{\partial}{\partial z} \left( \dfrac{z}{\tau^3} \right) = \dfrac{\tau^2 - 3z^2}{\tau^5}. \nonumber \]

Therefore,

\[ \begin{align*} \text{div } \vecs F_{\tau} &= \dfrac{\tau^2 - 3x^2}{\tau^5} + \dfrac{\tau^2 - 3y^2}{\tau^5} + \dfrac{\tau^2 - 3z^2}{\tau^5} \\[4pt]
&= \dfrac{3\tau^2 - 3(x^2+y^2+z^2)}{\tau^5} \\[4pt]
&= \dfrac{3\tau^2 - 3\tau^2}{\tau^5} = 0. \end{align*}\]

Notice that since the divergence of \(\vecs F_{\tau}\) is zero and \(\vecs E\) is \(\vecs F_{\tau}\) scaled by a constant, the divergence of electrostatic field \(\vecs E\) is also zero (except at the origin).

Flux across a Smooth Surface

Let \(S\) be a connected, piecewise smooth closed surface and let \(\vecs F_{\tau} = \dfrac{1}{\tau^2} \left\langle \dfrac{x}{\tau}, \, \dfrac{y}{\tau}, \, \dfrac{z}{\tau}\right \rangle\). Then,

\[\iint_S \vecs F_{\tau} \cdot d\vecs S = \begin{cases}0, & \text{if }S\text{ does not encompass the origin} \\ 4\pi, & \text{if }S\text{ encompasses the origin.} \end{cases} \nonumber \]

In other words, this theorem says that the flux of \(\vecs F_{\tau}\) across any piecewise smooth closed surface \(S\) depends only on whether the origin is inside of \(S\).

Proof

The logic of this proof follows the logic of [link], only we use the divergence theorem rather than Green’s theorem.

First, suppose that \(S\) does not encompass the origin. In this case, the solid enclosed by \(S\) is in the domain of \(\vecs F_{\tau}\), and since the divergence of \(\vecs F_{\tau}\) is zero, we can immediately apply the divergence theorem and find that \[\iint_S \vecs F \cdot d\vecs S \nonumber \] is zero.

Now suppose that \(S\) does encompass the origin. We cannot just use the divergence theorem to calculate the flux, because the field is not defined at the origin. Let \(S_a\) be a sphere of radius a inside of \(S\) centered at the origin. The outward normal vector field on the sphere, in spherical coordinates, is

\[\vecs t_{\phi} \times \vecs t_{\theta} = \langle a^2 \cos \theta \, \sin^2 \phi, \, a^2 \sin \theta \, \sin^2 \phi, \, a^2 \sin \phi \, \cos \phi \rangle \nonumber \]

(see [link]). Therefore, on the surface of the sphere, the dot product \(\vecs F_{\tau} \cdot \vecs N\) (in spherical coordinates) is

\[ \begin{align*} \vecs F_{\tau} \cdot \vecs N &= \left \langle \dfrac{\sin \phi \, \cos \theta}{a^2}, \, \dfrac{\sin \phi \, \sin \theta}{a^2}, \, \dfrac{\cos \phi}{a^2} \right \rangle \cdot \langle a^2 \cos \theta \, \sin^2 \phi, a^2 \sin \theta \, \sin^2 \phi, \, a^2 \sin \phi \, \cos \phi \rangle \\[4pt]
&= \sin \phi ( \langle \sin \phi \, \cos \theta, \, \sin \phi \, \sin \theta, \, \cos \phi \rangle \cdot \langle \sin \phi \, \cos \theta, \sin \phi \, \sin \theta, \, \cos \phi \rangle ) \\[4pt]
&= \sin \phi. \end{align*}\]

The flux of \(\vecs F_{\tau}\) across \(S_a\) is

\[\iint_{S_a} \vecs F_{\tau} \cdot \vecs N dS = \int_0^{2\pi} \int_0^{\pi} \sin \phi \, d\phi \, d\theta = 4\pi. \nonumber \]

Now, remember that we are interested in the flux across \(S\), not necessarily the flux across \(S_a\). To calculate the flux across \(S\), let \(E\) be the solid between surfaces \(S_a\) and \(S\). Then, the boundary of \(E\) consists of \(S_a\) and \(S\). Denote this boundary by \(S - S_a\) to indicate that \(S\) is oriented outward but now \(S_a\) is oriented inward. We would like to apply the divergence theorem to solid \(E\). Notice that the divergence theorem, as stated, can’t handle a solid such as \(E\) because \(E\) has a hole. However, the divergence theorem can be extended to handle solids with holes, just as Green’s theorem can be extended to handle regions with holes. This allows us to use the divergence theorem in the following way. By the divergence theorem,

\[ \begin{align*} \iint_{S-S_a} \vecs F_{\tau} \cdot d\vecs S &= \iint_S \vecs F_{\tau} \cdot d\vecs S - \iint_{S_a} \vecs F_{\tau} \cdot d\vecs S \\[4pt]
&= \iiint_E \text{div } \vecs F_{\tau} \, dV \\[4pt]
&= \iiint_E 0 \, dV = 0. \end{align*}\]

Therefore,

\[\iint_S \vecs F_{\tau} \cdot d\vecs S = \iint_{S_a} \vecs F_{\tau} \cdot d\vecs S = 4\pi, \nonumber \]

and we have our desired result.

\(\Box\)

Now we return to calculating the flux across a smooth surface in the context of electrostatic field \(\vecs E = \dfrac{q}{4\pi \epsilon_0} \vecs F_{\tau} \) of a point charge at the origin. Let \(S\) be a piecewise smooth closed surface that encompasses the origin. Then

\[ \begin{align*} \iint_S \vecs E \cdot d\vecs S &= \iint_S \dfrac{q}{4\pi \epsilon_0} \vecs F_{\tau} \cdot d\vecs S\\[4pt]
&= \dfrac{q}{4\pi \epsilon_0} \iint_S \vecs F_{\tau} \cdot d\vecs S \\[4pt]
&= \dfrac{q}{\epsilon_0}. \end{align*}\]

If \(S\) does not encompass the origin, then

\[\iint_S \vecs E \cdot d\vecs S = \dfrac{q}{4\pi \epsilon_0} \iint_S \vecs F_{\tau} \cdot d\vecs S = 0. \nonumber \]

Therefore, we have justified the claim that we set out to justify: the flux across closed surface \(S\) is zero if the charge is outside of \(S\), and the flux is \(q/\epsilon_0\) if the charge is inside of \(S\).

This analysis works only if there is a single point charge at the origin. In this case, Gauss’ law says that the flux of \(\vecs E\) across \(S\) is the total charge enclosed by \(S\). Gauss’ law can be extended to handle multiple charged solids in space, not just a single point charge at the origin. The logic is similar to the previous analysis, but beyond the scope of this text. In full generality, Gauss’ law states that if \(S\) is a piecewise smooth closed surface and \(Q\) is the total amount of charge inside of \(S\), then the flux of \(\vecs E\) across \(S\) is \(Q/\epsilon_0\).

Example \(\PageIndex{5}\): Using Gauss’ law

Suppose we have four stationary point charges in space, all with a charge of 0.002 Coulombs (C). The charges are located at \((0,0,1), \, (1,1,4), (-1,0,0)\), and \((-2,-2,2)\). Let \(\vecs E\) denote the electrostatic field generated by these point charges. If \(S\) is the sphere of radius \(2\) oriented outward and centered at the origin, then find

\[\iint_S \vecs E \cdot d\vecs S. \nonumber \]

Solution

According to Gauss’ law, the flux of \(\vecs E\) across \(S\) is the total charge inside of \(S\) divided by the electric constant. Since \(S\) has radius \(2\), notice that only two of the charges are inside of \(S\): the charge at \(0,1,1)\) and the charge at \((-1,0,0)\). Therefore, the total charge encompassed by \(S\) is \(0.004\) and, by Gauss’ law,

\[\iint_S \vecs E \cdot d\vecs S = \dfrac{0.004}{8.854 \times 10^{-12}} \approx 4.418 \times 10^9 \, V - m. \nonumber \]

Exercise \(\PageIndex{4}\)

Work the previous example for surface \(S\) that is a sphere of radius 4 centered at the origin, oriented outward.

Hint

Use Gauss’ law.

Answer

\(\approx 6.777 \times 10^9\)

Key Concepts

• The divergence theorem relates a surface integral across closed surface \(S\) to a triple integral over the solid enclosed by \(S\). The divergence theorem is a higher dimensional version of the flux form of Green’s theorem, and is therefore a higher dimensional version of the Fundamental Theorem of Calculus.
• The divergence theorem can be used to transform a difficult flux integral into an easier triple integral and vice versa.
• The divergence theorem can be used to derive Gauss’ law, a fundamental law in electrostatics.

Key Equations

• Divergence theorem \[\iiint_E \text{div } \vecs F \, dV = \iint_S \vecs F \cdot d\vecs S \nonumber \]

Glossary

divergence theorem

a theorem used to transform a difficult flux integral into an easier triple integral and vice versa

Gauss’ law

if S is a piecewise, smooth closed surface in a vacuum and \(Q\) is the total stationary charge inside of \(S\), then the flux of electrostatic field \(\vecs E\) across \(S\) is \(Q/\epsilon_0\)

inverse-square law

the electrostatic force at a given point is inversely proportional to the square of the distance from the source of the charge