17.3: Aplicaciones de Ecuaciones Diferenciales de Segundo Orden

Última actualización
Guardar como PDF

Page ID: 116297

Edwin “Jed” Herman & Gilbert Strang
OpenStax

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

Resuelve una ecuación diferencial de segundo orden que representa el movimiento armónico simple.
Resuelve una ecuación diferencial de segundo orden que representa el movimiento armónico simple amortiguado.
Resuelve una ecuación diferencial de segundo orden que representa el movimiento armónico simple forzado.
Resuelve una ecuación diferencial de segundo orden que representa la carga y la corriente en un circuito en serie RLC.

Vimos en la introducción del capítulo que las ecuaciones diferenciales lineales de segundo orden se utilizan para modelar muchas situaciones en física e ingeniería. En esta sección, analizamos cómo funciona esto para sistemas de un objeto con masa unida a un resorte vertical y un circuito eléctrico que contiene una resistencia, un inductor y un condensador conectados en serie. Modelos como estos pueden utilizarse para aproximarse a otras situaciones más complicadas; por ejemplo, los enlaces entre átomos o moléculas suelen modelarse como resortes que vibran, como describen estas mismas ecuaciones diferenciales.

Movimiento armónico simple

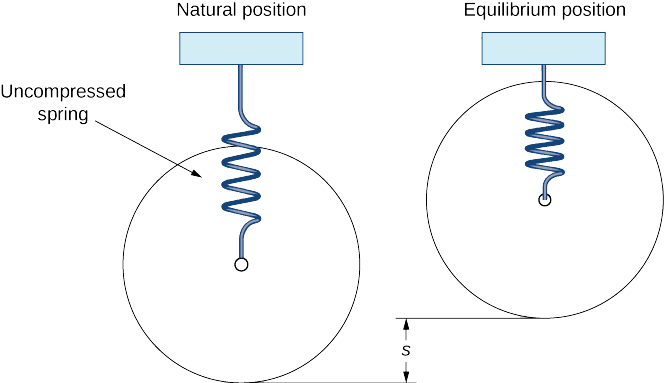
Considera una masa suspendida de un resorte unido a un soporte rígido. (Esto se llama comúnmente un sistema de masa de resorte). La gravedad está tirando de la masa hacia abajo y la fuerza restauradora del resorte está tirando de la masa hacia arriba. Como se muestra en la Figura\(\PageIndex{1}\), cuando estas dos fuerzas son iguales, se dice que la masa está en la posición de equilibrio. Si la masa se desplaza del equilibrio, oscila hacia arriba y hacia abajo. Este comportamiento se puede modelar mediante una ecuación diferencial de coeficiente constante de segundo orden.

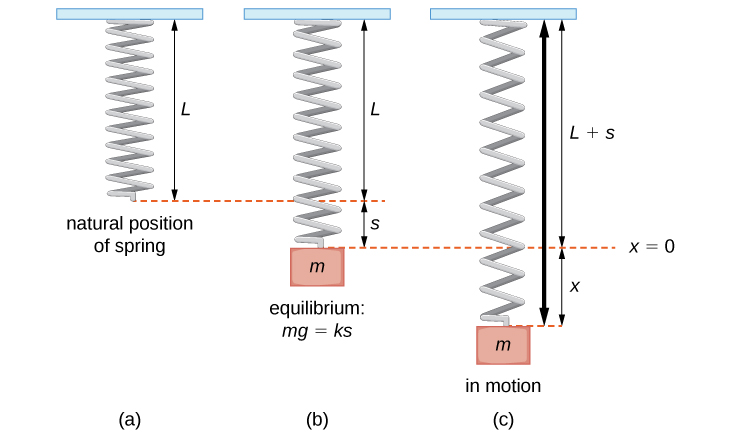
Esta figura tiene tres imágenes de resortes. La primera imagen es un resorte vertical en su posición natural con longitud L unida en la parte superior a un punto fijo. La segunda imagen muestra un resorte vertical con una masa m unida al resorte, estirando la distancia del muelle s de L. El resorte está en equilibrio. La tercera imagen es un resorte vertical con masa m unida donde el resorte está en movimiento, distancia x del equilibrio L + s. — Figura\(\PageIndex{1}\): Un resorte en su posición natural (a), en equilibrio con una masa m unida (b), y en movimiento oscilatorio (c).

Dejar\(x(t)\) denotar el desplazamiento de la masa desde el equilibrio. Obsérvese que para los sistemas de masa-resorte de este tipo, se acostumbra adoptar la convención de que la bajada es positiva. Así, un desplazamiento positivo indica que la masa está por debajo del punto de equilibrio, mientras que un desplazamiento negativo indica que la masa está por encima del equilibrio. El desplazamiento generalmente se da en pies en el sistema inglés o metros en el sistema métrico.

Considera las fuerzas que actúan sobre la masa. La fuerza de gravedad viene dada por mg.mg. En el sistema inglés, la masa está en babosas y la aceleración resultante de la gravedad es en pies por segundo al cuadrado. La aceleración resultante de la gravedad es constante, así que en el sistema inglés,\(g=32\, ft/sec^2\). Recordemos que 1 babosa pie/seg ² es una libra, por lo que la expresión mg se puede expresar en libras. Las unidades métricas del sistema son kilogramos para la masa y m/seg ² para la aceleración gravitacional. En el sistema métrico, tenemos\(g=9.8\) m/seg ².

Según la ley de Hooke, la fuerza restauradora del resorte es proporcional al desplazamiento y actúa en sentido contrario al desplazamiento, por lo que la fuerza restauradora viene dada por\(−k(s+x).\) La constante de resorte se da en libras por pie en el sistema inglés y en newtons por metro en el sistema métrico.

Ahora, por la segunda ley de Newton, la suma de las fuerzas en el sistema (gravedad más la fuerza restauradora) es igual a la masa por aceleración, así que tenemos

\[\begin{align*}mx″ &=−k(s+x)+mg \\[4pt] &=−ks−kx+mg. \end{align*}\]

Sin embargo, por cierto hemos definido nuestra posición de equilibrio,\(mg=ks\), la ecuación diferencial se vuelve

\[mx″+kx=0. \nonumber \]

Es conveniente reorganizar esta ecuación e introducir una nueva variable, llamada la frecuencia angular,\(ω\). Dejando\(ω=\sqrt{k/m}\), podemos escribir la ecuación como

\[x''+ω^2x=0. \nonumber \]

Esta ecuación diferencial tiene la solución general

\[x(t)=c_1 \cos ωt+c_2 \sin ωt, \label{GeneralSol} \]

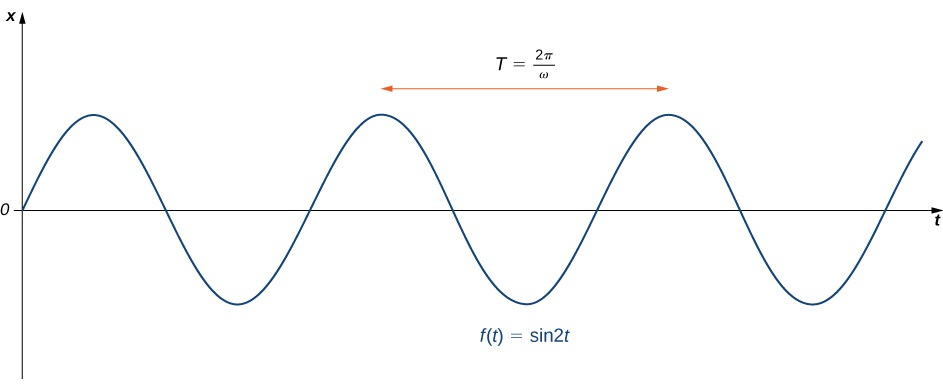
que da la posición de la masa en cualquier momento. El movimiento de la masa se llama movimiento armónico simple. El periodo de este movimiento (el tiempo que se tarda en completar una oscilación) es\(T=\dfrac{2π}{ω}\) y la frecuencia es\(f=\dfrac{1}{T}=\dfrac{ω}{2π}\) (Figura\(\PageIndex{2}\)).

Esta cifra es la gráfica de f (t) = sin 2t. Se trata de una gráfica periódica, oscilante. El periodo de la gráfica se representa con una línea apuntando de un pico al siguiente. Se etiqueta con el periodo T = 2π/ω. — Figura\(\PageIndex{2}\): Gráfica de desplazamiento vertical versus tiempo para movimiento armónico simple.

Ejemplo\(\PageIndex{1}\): Simple Harmonic Motion

Supongamos que un objeto que pesa 2 lb estira un resorte de 6 pulgadas. Encuentre la ecuación de movimiento si el resorte se libera de la posición de equilibrio con una velocidad ascendente de 16 pies/seg. ¿Cuál es el periodo de la moción?

Solución

Primero tenemos que encontrar la constante primaveral. Tenemos

\[\begin{align*}mg &=ks\\[4pt] 2 &=k \left(\dfrac{1}{2}\right)\\[4pt] k &=4. \end{align*}\]

También sabemos que el peso\(W\) es igual al producto de la masa\(m\) y la aceleración por gravedad\(g\). En unidades inglesas, la aceleración por gravedad es de 32 pies/seg ².

\[\begin{align*}W &=mg\\[4pt] 2 &=m(32)\\[4pt] m &=\dfrac{1}{16}\end{align*}\]

Así, la ecuación diferencial que representa este sistema es

\[\dfrac{1}{16}x″+4x=0. \nonumber \]

Multiplicando por 16, obtenemos\(x''+64x=0,\) que también se puede escribir en la forma\(x''+(8^2)x=0.\) Esta ecuación tiene la solución general

\[x(t)=c_1 \cos (8t)+c_2 \sin (8t). \nonumber \]

La masa se liberó de la posición de equilibrio\(x(0)=0\), así, y tuvo una velocidad ascendente inicial de 16 pies/seg, entonces\(x′(0)=−16\). Aplicando estas condiciones iniciales para resolver para\(c_1\) y\(c_2\). da

\[x(t)=−2 \sin 8t. \nonumber \]

El periodo de esta moción es el\(\dfrac{2π}{8}=\dfrac{π}{4}\) sec.

Ejercicio\(\PageIndex{1}\)

Una masa de 200 g estira un resorte de 5 cm. Encuentra la ecuación de movimiento de la masa si se libera del reposo desde una posición 10 cm por debajo de la posición de equilibrio. ¿Cuál es la frecuencia de este movimiento?

Pista: Primero encuentra la constante primaveral.

Responder: \(x(t)=0.1 \cos (14t)\)(en metros); la frecuencia es\(\dfrac{14}{2π}\) Hz.

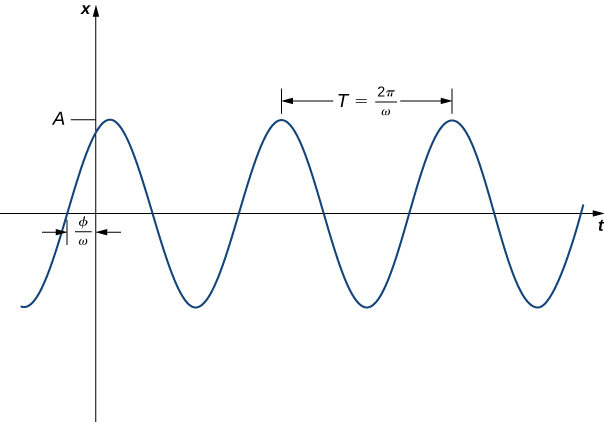
Escribir la solución general en la forma\(x(t)=c_1 \cos (ωt)+c_2 \sin(ωt)\) (Ecuación\ ref {GeneralSol}) tiene algunas ventajas. Es fácil ver el vínculo entre la ecuación diferencial y la solución, y el período y la frecuencia del movimiento son evidentes. Esta forma de la función nos dice muy poco sobre la amplitud del movimiento, sin embargo. En algunas situaciones, podemos preferir escribir la solución en la forma

\[x(t)=A \sin (ωt+ϕ). \nonumber \]

Si bien el vínculo con la ecuación diferencial no es tan explícito en este caso, el periodo y la frecuencia del movimiento siguen siendo evidentes. Además, la amplitud del movimiento,\(A,\) es obvia en esta forma de la función. La constante\(ϕ\) se denomina desplazamiento de fase y tiene el efecto de desplazar la gráfica de la función hacia la izquierda o la derecha.

Para convertir la solución a esta forma, queremos encontrar los valores de\(A\) y\(ϕ\) tal que

\[c_1 \cos (ωt)+c_2 \sin (ωt)=A \sin (ωt+ϕ). \nonumber \]

Primero aplicamos la identidad trigonométrica

\[\sin (α+β)= \sin α \cos β+ \cos α \sin β \nonumber \]

para obtener

\[\begin{align*} c_1 \cos (ωt)+c_2 \sin (ωt) &= A( \sin (ωt) \cos ϕ+ \cos (ωt) \sin ϕ) \\[4pt] &= A \sin ϕ( \cos (ωt))+A \cos ϕ( \sin (ωt)). \end{align*}\]

Así,

\[c1=A \sin ϕ \text{ and } c_2=A \cos ϕ. \nonumber \]

Si cuadramos ambas ecuaciones y las sumamos juntas, obtenemos

\[\begin{align*}c_1^2+c_2^2 &=A^2 \sin _2 ϕ+A^2 \cos _2 ϕ \\[4pt] &=A^2( \sin ^2 ϕ+ \cos ^2 ϕ) \\[4pt] &=A^2. \end{align*}\]

Así,

\[A=\sqrt{c_1^2+c_2^2}. \nonumber \]

Ahora, para encontrar\(ϕ\), volver a las ecuaciones para\(c_1\) y\(c_2\), pero esta vez, dividir la primera ecuación por la segunda ecuación para obtener

\[\begin{align*} \dfrac{c_1}{c_2} &=\dfrac{A \sin ϕ}{A \cos ϕ} \\[4pt] &= \tan ϕ. \end{align*} \nonumber \]

Entonces,

\[\tan ϕ= \dfrac{c_1}{c_2}. \nonumber \]

Resumimos este hallazgo en el siguiente teorema.

Solución a la ecuación para el movimiento armónico simple

La función se\(x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\) puede escribir en la forma\(x(t)=A \sin (ωt+ϕ)\), dónde\(A=\sqrt{c_1^2+c_2^2}\) y\( \tan ϕ = \dfrac{c_1}{c_2}\).

Tenga en cuenta que al usar la fórmula\( \tan ϕ=\dfrac{c_1}{c_2}\) para encontrar\(ϕ\), debemos tener cuidado de asegurar que\(ϕ\) esté en el cuadrante derecho (Figura\(\PageIndex{3}\)).

Ejemplo\(\PageIndex{2}\): Expressing the Solution with a Phase Shift

Expresar las siguientes funciones en el formulario\(A \sin (ωt+ϕ) \). ¿Cuál es la frecuencia del movimiento? ¿La amplitud?

\(x(t)=2 \cos (3t)+ \sin (3t)\)
\(x(t)=3 \cos (2t)−2 \sin (2t)\)

Solución

Tenemos

\[A=\sqrt{c_1^2+c_2^2}=\sqrt{2^2+1^2}=\sqrt{5} \nonumber \]

\[ \tan ϕ = \dfrac{c_1}{c_2}=\dfrac{2}{1}=2. \nonumber \]

Obsérvese que ambos\(c_1\) y\(c_2\) son positivos, así\(ϕ\) es en el primer cuadrante. Así,

\[ϕ≈1.107 \; \text{rad}, \nonumber \]

así que tenemos

\[ x(t) = 2 \cos (3t)+ \sin (3t) =5 \sin (3t+1.107). \nonumber \]

La frecuencia es\(\dfrac{ω}{2π}=\dfrac{3}{2π}≈0.477.\) La amplitud es\(\sqrt{5}\).

Tenemos
\[A=\sqrt{c_1^2+c_2^2}=\sqrt{3^2+2^2}=\sqrt{13} \nonumber \]
y
\[ \tan ϕ = \dfrac{c_1}{c_2}= \dfrac{3}{−2}=−\dfrac{3}{2}. \nonumber \]
Tenga en cuenta que\(c_1\) es positivo pero\(c_2\) es negativo, así\(ϕ\) es en el cuarto cuadrante. Por lo tanto,
\[ϕ≈−0.983 \; \text{rad}, \nonumber \]
por lo que tenemos
\[\begin{align*} x(t) &=3 \cos (2t) −2 \sin (2t) \\ &= \sqrt{13} \sin (2t−0.983). \end{align*}\]
La frecuencia es\(\dfrac{ω}{2π}=\dfrac{2}{2π}≈0.318.\) La amplitud es\(\sqrt{13}\).

Ejercicio\(\PageIndex{2}\)

Exprese la función\(x(t)= \cos (4t) + 4 \sin (4t)\) en el formulario\(A \sin (ωt+ϕ) \). ¿Cuál es la frecuencia del movimiento? ¿La amplitud?

Pista: Utilice el proceso del Ejemplo\(\PageIndex{2}\).

Responder: \(x(t)= \sqrt{17} \sin (4t+0.245), \text{frequency} =\dfrac{4}{2π}≈0.637, A=\sqrt{17}\)

Vibraciones amortiguadas

Con el modelo recién descrito, el movimiento de la masa continúa indefinidamente. Claramente, esto no sucede en el mundo real. En el mundo real, casi siempre hay cierta fricción en el sistema, lo que hace que las oscilaciones mueran lentamente—un efecto llamado amortiguación. Entonces ahora veamos cómo incorporar esa fuerza de amortiguación en nuestra ecuación diferencial.

Los sistemas físicos de masa de resorte casi siempre tienen alguna amortiguación como resultado de la fricción, la resistencia al aire o un amortiguador físico, llamado amortiguador (un cilindro neumático; Figura\(\PageIndex{4}\)).

Esta cifra es un cilindro neumático. El cilindro es transparente, y se puede ver el pistón. — Figura\(\PageIndex{4}\): Un amortiguador es un cilindro neumático que amortigua el movimiento de un sistema oscilante.

Debido a que la amortiguación es principalmente una fuerza de fricción, asumimos que es proporcional a la velocidad de la masa y actúa en la dirección opuesta. Entonces la fuerza de amortiguación viene dada por\(−bx′\) para alguna constante\(b>0\). De nuevo aplicando la segunda ley de Newton, la ecuación diferencial se convierte en

\[mx″+bx′+kx=0. \nonumber \]

Entonces la ecuación característica asociada es

\[mλ^2+bλ+k=0. \nonumber \]

Aplicando la fórmula cuadrática, tenemos

\[λ=\dfrac{−b±\sqrt{b^2−4mk}}{2m}. \nonumber \]

Al igual que en las Ecuaciones Lineales de Segundo Orden consideramos tres casos, basados en si la ecuación característica tiene raíces reales distintas, una raíz real repetida o raíces conjugadas complejas.

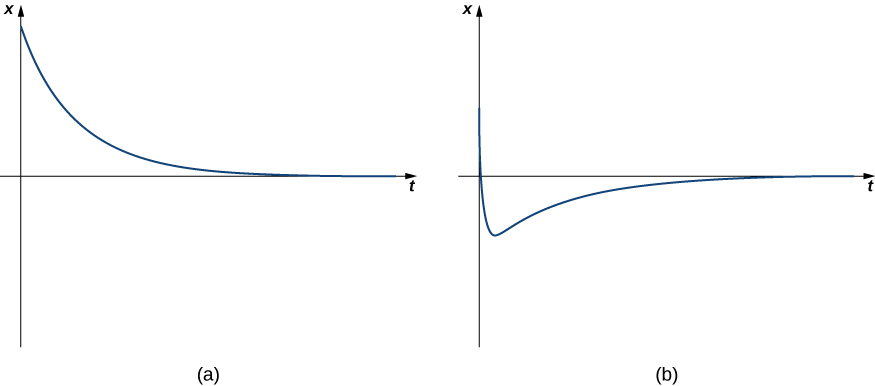
Caso 1: Vibraciones sobreamortiguadas

Cuando\(b^2>4mk\), decimos que el sistema está sobreamortiguado. La solución general tiene la forma

\[x(t)=c_1e^{λ_1t}+c_2e^{λ_2t}, \nonumber \]

donde ambos\(λ_1\) y\(λ_2\) son menores que cero. Debido a que los exponentes son negativos, el desplazamiento decae a cero con el tiempo, generalmente con bastante rapidez. Los sistemas sobreamortiguados no oscilan (no más de un cambio de dirección), sino que simplemente retroceden hacia la posición de equilibrio. La figura\(\PageIndex{5}\) muestra cómo es el comportamiento típico de amortiguamiento crítico.

Esta figura tiene dos gráficas etiquetadas (a) y (b). La primera gráfica es una curva decreciente con el eje horizontal como asíntota horizontal. La segunda gráfica inicialmente es una función decreciente pero se vuelve creciente por debajo del eje horizontal. Entonces, el eje horizontal es también una asíntota horizontal. — Figura\(\PageIndex{5}\): Comportamiento de un sistema de masa de resorte sobreamortiguado, sin cambio de dirección (a) y solo un cambio de dirección (b).

Ejemplo\(\PageIndex{3}\): Overdamped Spring-Mass System

Una masa de 16 lb está unida a un resorte de 10 pies. Cuando la masa llega a descansar en la posición de equilibrio, el resorte mide 15 pies 4 in. El sistema se sumerge en un medio que imparte una fuerza de amortiguación igual a 5252 veces la velocidad instantánea de la masa. Encuentra la ecuación de movimiento si la masa es empujada hacia arriba desde la posición de equilibrio con una velocidad ascendente inicial de 5 pies/seg. ¿Cuál es la posición de la masa después de 10 seg? ¿Su velocidad?

Solución

La masa estira el resorte 5 pies 4 in., o\(\dfrac{16}{3}\) ft. Así,\(16=\left(\dfrac{16}{3}\right)k,\) así también\(k=3.\) tenemos\(m=\dfrac{16}{32}=\dfrac{1}{2}\), por lo que la ecuación diferencial es

\[\dfrac{5}{2}x′+3x=0. \nonumber \]

Multiplicando por 2 da\(x″+5x′+6x=0\), que tiene la solución general

\[x(t)=c_1e^{−2t}+c_2e^{−3t}. \nonumber \]

Aplicando las condiciones iniciales,\(x(0)=0\) y\(x′(0)=−5\), obtenemos

\[x(t)=−5e^{−2t}+5e^{−3t}. \nonumber \]

Después de 10 seg, la masa está en posición

\[x(10)=−5e^{−20}+5e^{−30}≈−1.0305×10^{−8}≈0, \nonumber \]

así es, efectivamente, en la posición de equilibrio. Tenemos\(x′(t)=10e^{−2t}−15e^{−3t}\), así que después de 10 seg la masa se mueve a una velocidad de

\[x′(10)=10e^{−20}−15e^{−30}≈2.061×10^{−8}≈0. \nonumber \]

Después de sólo 10 seg, la masa apenas se mueve.

Ejercicio\(\PageIndex{3}\)

Se une una masa de 2 kg a un resorte con constante de resorte de 24 N/m. El sistema se sumerge luego en un medio impartiendo una fuerza de amortiguación igual a 16 veces la velocidad instantánea de la masa. Encuentra la ecuación de movimiento si se libera del reposo en un punto 40 cm por debajo del equilibrio.

Pista: Sigue el proceso del ejemplo anterior.

Responder: \(x(t)=0.6e^{−2t}−0.2e^{−6t}\)

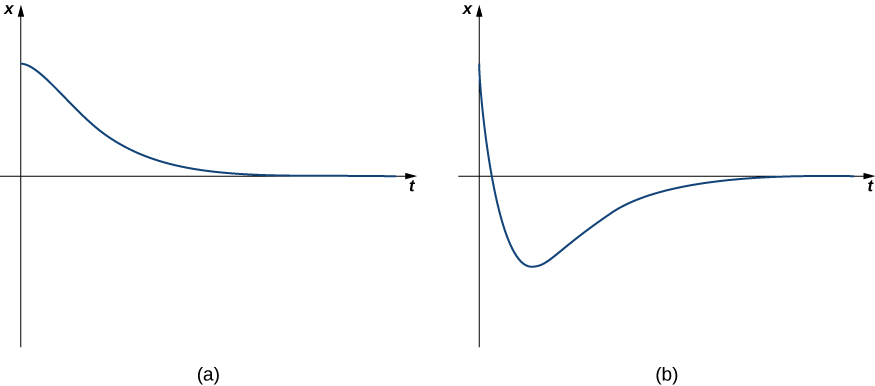
Caso 2: Vibraciones amortiguadas críticamente

Cuando\(b^2=4mk\), decimos que el sistema está críticamente amortiguado. La solución general tiene la forma

\[x(t)=c_1e^{λ_1t}+c_2te^{λ_1t}, \nonumber \]

donde\(λ_1\) es menor que cero. El movimiento de un sistema amortiguado críticamente es muy similar al de un sistema sobreamortiguado. No oscila. Sin embargo, con un sistema críticamente amortiguado, si la amortiguación se reduce incluso un poco, se produce un comportamiento oscilatorio. Desde una perspectiva práctica, los sistemas físicos casi siempre están sobreamortiguados o poco amortiguados (caso 3, que consideramos siguiente). Es imposible afinar las características de un sistema físico para que\(b^2\) y\(4mk\) sean exactamente iguales. La figura\(\PageIndex{6}\) muestra cómo es el comportamiento típico de amortiguamiento crítico.

Esta figura tiene dos gráficas etiquetadas (a) y (b). La primera gráfica se encuentra en el primer cuadrante y es una curva decreciente con el eje horizontal como asíntota horizontal. La segunda gráfica inicialmente es una función decreciente pero se vuelve creciente por debajo del eje horizontal. Entonces, el eje horizontal es también una asíntota horizontal. — Figura\(\PageIndex{6}\): Comportamiento de un sistema de masa de resorte amortiguado críticamente. El sistema graficado en la parte (a) tiene más amortiguación que el sistema graficado en la parte (b).

Ejemplo\(\PageIndex{4}\): Critically Damped Spring-Mass System

Una masa de 1 kg estira un resorte de 20 cm. El sistema está unido a un amortiguador que imparte una fuerza de amortiguación igual a 14 veces la velocidad instantánea de la masa. Encuentra la ecuación de movimiento si la masa se libera del equilibrio con una velocidad ascendente de 3 m/seg.

Solución

Tenemos\(mg=1(9.8)=0.2k\),\(k=49.\) entonces entonces, la ecuación diferencial es

\[x″+14x′+49x=0, \nonumber \]

que tiene solución general

\[x(t)=c_1e^{−7t}+c_2te^{−7t}. \nonumber \]

Aplicando las condiciones iniciales\(x(0)=0\) y\(x′(0)=−3\) da

\[x(t)=−3te^{−7t}. \nonumber \]

Ejercicio\(\PageIndex{4}\)

Un peso de 1 lb estira un resorte de 6 pulg., y el sistema está unido a un amortiguador que imparte una fuerza de amortiguación igual a la mitad de la velocidad instantánea de la masa. Encuentra la ecuación de movimiento si la masa se libera del reposo en un punto 6 pulg. por debajo del equilibrio.

Pista: Primero encuentra la constante primaveral.

Responder: \(x(t)=\dfrac{1}{2}e^{−8t}+4te^{−8t} \)

Caso 3: Vibraciones sin amortiguar

Cuando\(b^2<4mk\), decimos que el sistema está subamortiguado. La solución general tiene la forma

\[x(t)=e^{αt}(c_1 \cos (βt) + c_2 \sin (βt)), \nonumber \]

donde\(α\) es menor que cero. Los sistemas subamortiguados oscilan debido a los términos de seno y coseno en la solución. Sin embargo, el término exponencial domina eventualmente, por lo que la amplitud de las oscilaciones disminuye con el tiempo. La figura\(\PageIndex{7}\) muestra cómo se ve el comportamiento típico de poca humedad.

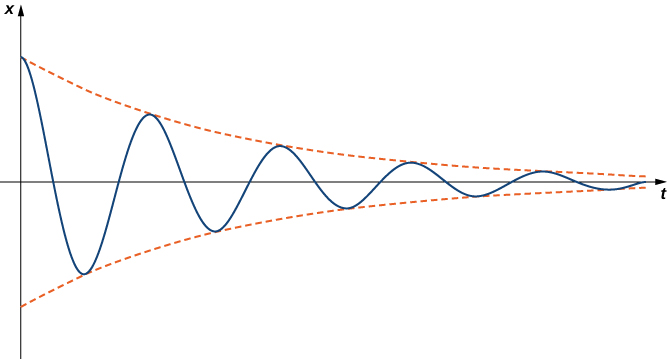
Esta figura es una gráfica oscilante donde la amplitud es decreciente. Hay curvas discontinuas rojas en los picos de las amplitudes que muestran el patrón de una amplitud decreciente. A medida que t aumenta, el eje horizontal se convierte en una asíntota horizontal. — Figura\(\PageIndex{7}\): Comportamiento de un sistema de masa de resorte con amortiguación insuficiente.

Tenga en cuenta que para todos los sistemas amortiguados,\( \lim \limits_{t \to \infty} x(t)=0\). El sistema siempre se acerca a la posición de equilibrio en el tiempo.

Ejemplo\(\PageIndex{5}\): Underdamped Spring-Mass System

Un peso de 16 lb estira un resorte de 3.2 pies. Supongamos que la fuerza de amortiguación en el sistema es igual a la velocidad instantánea de la masa. Encuentra la ecuación de movimiento si la masa se libera del reposo en un punto de 9 pulg. por debajo del equilibrio.

Solución

Tenemos\(k=\dfrac{16}{3.2}=5\) y\(m=\dfrac{16}{32}=\dfrac{1}{2},\) así la ecuación diferencial es

\[\dfrac{1}{2} x″+x′+5x=0, \; \text{or} \; x″+2x′+10x=0. \nonumber \]

Esta ecuación tiene la solución general

\[x(t)=e^{−t} ( c_1 \cos (3t)+c_2 \sin (3t) ) . \nonumber \]

Aplicando las condiciones iniciales,\(x(0)=\dfrac{3}{4}\) y\(x′(0)=0,\) obtenemos

\[x(t)=e^{−t} \bigg( \dfrac{3}{4} \cos (3t)+ \dfrac{1}{4} \sin (3t) \bigg) . \nonumber \]

Ejercicio\(\PageIndex{5}\)

Una masa de 1 kg estira un resorte 49 cm. El sistema se sumerge en un medio que imparte una fuerza de amortiguación igual a cuatro veces la velocidad instantánea de la masa. Encuentra la ecuación de movimiento si la masa se libera del reposo en un punto 24 cm por encima del equilibrio.

Pista: Primero encuentra la constante primaveral.

Responder: \(x(t)=−0.24e^{−2t} \cos (4t)−0.12e^{−2t} \sin (4t) \)

Ejemplo\(\PageIndex{6}\): Chapter Opener: Modeling a Motorcycle Suspension System

Para los pilotos de motocross, los sistemas de suspensión en sus motocicletas son muy importantes. Los recorridos todoterreno en los que circulan suelen incluir saltos, y perder el control de la motocicleta cuando aterrizan podría costarles la carrera.

Esta imagen es un amortiguador en una motocicleta. — Figura\(\PageIndex{8}\): (crédito: modificación de obra por NSeika, Flickr)

Este sistema de suspensión se puede modelar como un sistema amortiguado de masa de resorte. Definimos nuestro marco de referencia con respecto al marco de la motocicleta. Supongamos que el extremo del amortiguador unido al cuadro de la motocicleta es fijo. Entonces, la “masa” en nuestro sistema de resorte-masa es la rueda de la motocicleta. Medimos la posición de la rueda con respecto al cuadro de la motocicleta. Esto puede parecer contrario a la intuición, ya que, en muchos casos, en realidad es el cuadro de la motocicleta el que se mueve, pero este marco de referencia preserva el desarrollo de la ecuación diferencial que se hizo antes. Al igual que con el desarrollo anterior, definimos la dirección descendente para que sea positiva.

Cuando la motocicleta es levantada por su marco, la rueda cuelga libremente y el resorte queda sin comprimir. Esta es la posición natural del resorte. Cuando la motocicleta se coloca en el suelo y el piloto la monta, el resorte se comprime y el sistema se encuentra en la posición de equilibrio (Figura\(\PageIndex{9}\)).

Esta figura tiene dos resortes unidos arriba en un punto fijo. El primer resorte está etiquetado como “Posición Natural” y tiene un resorte sin comprimir que cuelga verticalmente. El segundo resorte está etiquetado como “Posición de Equilibrio” y tiene un resorte comprimido colgando verticalmente. La diferencia vertical entre los dos resortes está etiquetada como “s.” — Figura\(\PageIndex{9}\): Podemos utilizar un sistema de masa-resorte para modelar una suspensión de motocicleta.

Este sistema se puede modelar usando la misma ecuación diferencial que usamos antes:

\[mx″+bx′+kx=0. \nonumber \]

Una motocicleta de motocross pesa 204 lb, y asumimos un peso del ciclista de 180 lb Cuando el piloto monta la motocicleta, la suspensión comprime 4 pulg., luego llega a descansar en equilibrio. El sistema de suspensión proporciona una amortiguación igual a 240 veces la velocidad vertical instantánea de la motocicleta (y del piloto).

Establecer la ecuación diferencial que modele el comportamiento del sistema de suspensión de la motocicleta.
Nos interesa lo que sucede cuando la motocicleta aterriza después de dar un salto. Deje que el tiempo\[t=0 \nonumber \] denote el momento en que la motocicleta entra en contacto por primera vez con el Si la motocicleta choca contra el suelo con una velocidad de 10 pies/seg hacia abajo, encuentra la ecuación de movimiento de la motocicleta después del salto.
Grafica la ecuación de movimiento sobre el primer segundo después de que la motocicleta choca contra el suelo.

Solución

Hemos definido el equilibrio para ser el punto donde\(mg=ks\), así tenemos
\[\begin{align*} mg &=ks \\ 384 &=k\left(\dfrac{1}{3}\right)\\ k &=1152. \end{align*}\]

También contamos con

\[\begin{align*} W &=mg \\ 384 &=m(32) \\ m &=12. \end{align*}\]

Por lo tanto, la ecuación diferencial que modela el comportamiento de la suspensión de la motocicleta es

\[12x″+240x′+1152x=0. \nonumber \]

Dividiendo por 12, obtenemos

\[x''+20x′+96x=0. \nonumber \]
La ecuación diferencial que se encuentra en la parte a. tiene la solución general
\[x(t)=c_1e^{−8t}+c_2e^{−12t}. \nonumber \]

Ahora, para determinar nuestras condiciones iniciales, consideramos la posición y velocidad de la rueda de la motocicleta cuando la rueda entra en contacto por primera vez con el suelo. Dado que la motocicleta estaba en el aire antes de entrar en contacto con el suelo, la rueda colgaba libremente y el resorte estaba sin comprimir. Por lo tanto, la rueda es de 4 in. \(\left(\dfrac{1}{3}\text{ ft}\right)\)por debajo de la posición de equilibrio (con respecto al cuadro de la motocicleta), y tenemos\(x(0)=\dfrac{1}{3}.\) Según la declaración del problema, la motocicleta tiene una velocidad de 10 pies/seg hacia abajo cuando la motocicleta entra en contacto con el suelo, por lo que\(x′(0)=10.\) Aplicando estas condiciones iniciales, obtenemos\(c_1=\dfrac{7}{2}\) y \(c_2=−\left(\dfrac{19}{6}\right)\), por lo que la ecuación del movimiento es

\[x(t)=\dfrac{7}{2}e^{−8t}−\dfrac{19}{6}e^{−12t}. \nonumber \]
La gráfica se muestra en la Figura\(\PageIndex{10}\).

Esta figura es la gráfica de la función f (x) = 7/2e^−8t −19/6e^−12t. El eje vertical se escala en incrementos de 0.05, y el eje horizontal se etiqueta, “t”. Se escala en incrementos de décimas. La gráfica cruza el eje horizontal aumentando, alcanza un máximo, luego disminuye. El eje horizontal es una asíntota horizontal. — Figura\(\PageIndex{10}\): Gráfico de la ecuación de movimiento en un tiempo de un segundo.

VEHICULOS

La NASA está planeando una misión a Marte. Para ahorrar dinero, los ingenieros han decidido adaptar uno de los vehículos de alunizaje para la nueva misión. No obstante, les preocupa cómo las diferentes fuerzas gravitacionales afectarán al sistema de suspensión que amortigua la nave cuando aterrice. La aceleración resultante de la gravedad en la luna es de 1.6 m/seg ², mientras que en Marte es de 3.7 m/seg ².

El sistema de suspensión en la nave se puede modelar como un sistema amortiguado de masa de resorte. En este caso, el resorte se encuentra por debajo del módulo de aterrizaje lunar, por lo que el resorte se comprime ligeramente en equilibrio, como se muestra en la Figura\(\PageIndex{11}\).

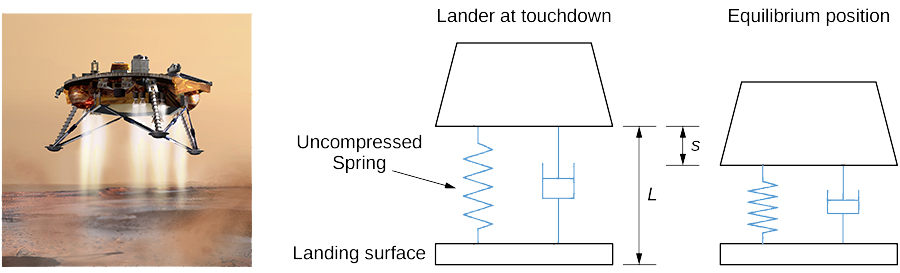
Esta figura tiene tres imágenes. El primero es una imagen del Mars Lander aterrizando en una superficie. La segunda imagen es un diagrama del Mars Lander en el touchdown, con un resorte sin comprimir con longitud L entre el Lander y la superficie de aterrizaje. La tercera imagen es un diagrama del Lander en posición de equilibrio después de que el Lander haya aterrizado. El resorte se comprime a una distancia de s. — Figura\(\PageIndex{11}\): La suspensión de lanchas de desembarco se puede representar como un sistema amortiguado de masa de resorte. (crédito “lander”: NASA)

Conservamos la convención de que a la baja es positiva. A pesar de la nueva orientación, un examen de las fuerzas que afectan al módulo de aterrizaje muestra que se puede utilizar la misma ecuación diferencial para modelar la posición de la embarcación de desembarco en relación con el equilibrio:

\[mx''+bx′+kx=0, \nonumber \]

donde\(m\) está la masa del módulo de aterrizaje,\(b\) es el coeficiente de amortiguación, y\(k\) es la constante de resorte.

El módulo de aterrizaje tiene una masa de 15,000 kg y el muelle mide 2 m de largo cuando no está comprimido. El módulo de aterrizaje está diseñado para comprimir el muelle 0.5 m para alcanzar la posición de equilibrio bajo la gravedad lunar. El amortiguador imparte una fuerza de amortiguación igual a 48,000 veces la velocidad instantánea del módulo de aterrizaje. Establecer la ecuación diferencial que modela el movimiento del módulo de aterrizaje cuando la nave aterriza en la luna.
Deje que el tiempo\(t=0\) denote el instante en que el módulo de aterrizaje aterriza. La velocidad de descenso del módulo de aterrizaje puede ser controlada por la tripulación, de manera que desciende a una velocidad de 2 m/seg cuando aterrice. Encuentra la ecuación de movimiento del módulo de aterrizaje en la luna.
Si el módulo de aterrizaje viaja demasiado rápido cuando toca hacia abajo, podría comprimir completamente el resorte y “tocar el fondo”. Tocando fondo podría dañar la embarcación de desembarco y debe evitarse a toda costa. Grafica la ecuación de movimiento que se encuentra en la parte 2. Si el muelle mide 0.5 m de largo cuando está completamente comprimido, ¿el módulo de aterrizaje estará en peligro de tocar fondo?
Suponiendo que los ingenieros de la NASA no hagan ajustes en el resorte o el amortiguador, ¿hasta dónde comprime el módulo de aterrizaje el resorte para alcanzar la posición de equilibrio bajo la gravedad marciana?
Si la tripulación del módulo de aterrizaje utiliza los mismos procedimientos en Marte que en la luna, y mantiene la tasa de descenso a 2 m/seg, ¿el módulo de aterrizaje tocará fondo cuando aterrice en Marte?
¿Qué ajustes, si los hubiera, deberían hacer los ingenieros de la NASA para usar el módulo de aterrizaje de manera segura en Marte?

Vibraciones Forzadas

El último caso que consideramos es cuando una fuerza externa actúa sobre el sistema. En el caso del sistema de suspensión de la motocicleta, por ejemplo, los baches en la carretera actúan como una fuerza externa que actúa sobre el sistema. Otro ejemplo es un resorte que cuelga de un soporte; si el soporte se pone en movimiento, ese movimiento se consideraría una fuerza externa sobre el sistema. Modelamos estos sistemas forzados con la ecuación diferencial no homogénea

\[mx″+bx′+kx=f(t), \nonumber \]

donde la fuerza externa está representada por el\(f(t)\) término. Como vimos en Ecuaciones Lineales No Homogénicas, ecuaciones diferenciales como esta tienen soluciones de la forma

\[x(t)=c_1x_1(t)+c_2x_2(t)+x_p(t), \nonumber \]

donde\(c_1x_1(t)+c_2x_2(t)\) es la solución general a la ecuación complementaria y\(x_p(t)\) es una solución particular a la ecuación no homogénea. Si el sistema está amortiguado,\(\lim \limits_{t \to \infty} c_1x_1(t)+c_2x_2(t)=0.\) ya que estos términos no afectan el comportamiento a largo plazo del sistema, llamamos a esta parte de la solución la solución transitoria. El comportamiento a largo plazo del sistema está determinado por\(x_p(t)\), por lo que llamamos a esta parte de la solución la solución de estado estacionario.

Ejemplo\(\PageIndex{7}\): Forced Vibrations

Una masa de 1 babosa estira un muelle de 2 pies y llega a descansar en equilibrio. El sistema está unido a un amortiguador que imparte una fuerza de amortiguación igual a ocho veces la velocidad instantánea de la masa. Encuentra la ecuación de movimiento si\(f(t)=8 \sin (4t)\) se aplica una fuerza externa igual a al sistema comenzando en el tiempo\(t=0\). ¿Cuál es la solución transitoria? ¿Cuál es la solución de estado estacionario?

Solución

Tenemos\(mg=1(32)=2k,\) así\(k=16\) y la ecuación diferencial es

\[x″+8x′+16x=8 \sin (4t). \nonumber \]

La solución general a la ecuación complementaria es

\[c_1e^{−4t}+c_2te^{−4t}. \nonumber \]

Asumiendo una solución particular de la forma\(x_p(t)=A \cos (4t)+ B \sin (4t)\) y utilizando el método de coeficientes indeterminados, encontramos\(x_p (t)=−\dfrac{1}{4} \cos (4t)\), entonces

\[x(t)=c_1e^{−4t}+c_2te^{−4t}−\dfrac{1}{4} \cos (4t). \nonumber \]

En\(t=0,\) la masa está en reposo en la posición de equilibrio, por lo que\(x(0)=x′(0)=0.\) Aplicando estas condiciones iniciales para resolver\(c_1\) y\(c_2,\) conseguimos

\[x(t)=\dfrac{1}{4}e^{−4t}+te^{−4t}−\dfrac{1}{4} \cos (4t). \nonumber \]

La solución transitoria es\(\dfrac{1}{4}e^{−4t}+te^{−4t}\). La solución de estado estacionario es\(−\dfrac{1}{4} \cos (4t).\)

Ejercicio\(\PageIndex{6}\)

Una masa de 2 kg se une a un resorte con 32 N/m constantes y llega a descansar en la posición de equilibrio. A partir del tiempo\(t=0\),\(f(t)=68e^{−2}t \cos (4t) \) se aplica al sistema una fuerza externa igual a. Encuentra la ecuación de movimiento si no hay amortiguación. ¿Cuál es la solución transitoria? ¿Cuál es la solución de estado estacionario?

Pista: Encuentre la solución particular antes de aplicar las condiciones iniciales.

Contestar

\(x(t)=−\dfrac{1}{2} \cos (4t)+ \dfrac{9}{4} \sin (4t)+ \dfrac{1}{2} e^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)

\(\text{Transient solution:} \dfrac{1}{2}e^{−2t} \cos (4t)−2e^{−2t} \sin (4t)\)

\(\text{Steady-state solution:} −\dfrac{1}{2} \cos (4t)+ \dfrac{9}{4} \sin (4t) \)

RESONCIA

Considere un sistema sin amortiguar que exhiba un movimiento armónico simple. En el mundo real, nunca tenemos realmente un sistema sin amortiguar; —siempre ocurre alguna amortiguación. Para fines teóricos, sin embargo, podríamos imaginar un sistema de masa de resorte contenido en una cámara de vacío. Sin resistencia al aire, la masa seguiría moviéndose hacia arriba y hacia abajo indefinidamente.

La frecuencia del movimiento resultante, dada por\(f=\dfrac{1}{T}=\dfrac{ω}{2π}\), se llama la frecuencia natural del sistema. Si una fuerza externa que actúa sobre el sistema tiene una frecuencia cercana a la frecuencia natural del sistema, resulta un fenómeno llamado resonancia. La fuerza externa refuerza y amplifica el movimiento natural del sistema.

Considera la ecuación diferencial\(x″+x=0.\) Encuentra la solución general. ¿Cuál es la frecuencia natural del sistema?
Ahora supongamos que este sistema está sujeto a una fuerza externa dada por\(f(t)=5 \cos t.\) Resolver el problema del valor inicial\(x″+x=5 \cos t\),\(x(0)=0\),\(x′(0)=1\).
Grafica la solución. ¿Qué pasa con el comportamiento del sistema a lo largo del tiempo?
En el mundo real, siempre hay alguna amortiguación. Sin embargo, si la fuerza de amortiguación es débil y la fuerza externa es lo suficientemente fuerte, los sistemas del mundo real aún pueden exhibir resonancia. Uno de los ejemplos más famosos de resonancia es el colapso del Puente Tacoma Narrows el 7 de noviembre de 1940. El puente había exhibido un comportamiento extraño desde que se construyó. La calzada tenía un extraño “rebote” a la misma. El día que colapsó, una fuerte tormenta de viento provocó que la calzada se torciera y ondulara violentamente. El puente no pudo soportar estas fuerzas y finalmente se derrumbó. Los expertos creen que la tormenta ejerció fuerzas sobre el puente que estaban muy cerca de su frecuencia natural, y la resonancia resultante finalmente sacudió el puente.
Este sitio web contiene más información sobre el colapso del Puente Tacoma Narrows.

Durante el poco tiempo se mantuvo el Puente Tacoma Narrows, se convirtió en toda una atracción turística. Varias personas estuvieron en el lugar el día que se derrumbó el puente, y una de ellas captó el colapso en una película.

Mira el video para ver el colapso del Puente Tacoma Narrows “Gallopin' Gertie”. https://www.youtube.com/watch?v=j-zczJXSxnw

Otro ejemplo de resonancia en el mundo real es una cantante destrozando una copa de vino de cristal cuando canta la nota correcta. Cuando alguien toca una copa de vino de cristal o moja un dedo y la corre alrededor del borde, se puede escuchar un tono. Esa nota es creada por la copa de vino que vibra a su frecuencia natural. Si entonces un cantante canta esa misma nota a un volumen suficientemente alto, el vidrio se rompe como resultado de la resonancia.
El programa de televisión Mythbusters transmitió un episodio sobre este fenómeno. Visita este sitio web para conocer más al respecto. Adam Savage también describió la experiencia. Mira este video para su cuenta.

El circuito de la serie RLC

Considere un circuito eléctrico que contenga una resistencia, un inductor y un condensador, como se muestra en la Figura\(\PageIndex{12}\). Tal circuito se llama circuito en serie RLC. Los circuitos RLC se utilizan en muchos sistemas electrónicos, especialmente como sintonizadores en radios AM/FM. La perilla de sintonización varía la capacitancia del condensador, que a su vez sintoniza la radio. Dichos circuitos pueden modelarse mediante ecuaciones diferenciales de coeficiente constante de segundo orden.

Dejar\(I(t)\) denotar la corriente en el circuito RLC y\(q(t)\) denotar la carga en el condensador. Además,\(L\) denotar inductancia en henrys (H),\(R\) denotar resistencia en ohmios\((Ω)\) y\(C\) denotar capacitancia en faradios (F). Por último, vamos a\(E(t)\) denotar el potencial eléctrico en voltios (V).

La regla de voltaje de Kirchhoff establece que la suma de las caídas de voltaje alrededor de cualquier bucle cerrado debe ser cero. Entonces, debemos considerar las caídas de voltaje a través del inductor (denotado\(E_L\)), la resistencia (denotado\(E_R\)) y el condensador (denotado\(E_C\)). Debido a que el circuito RLC que se muestra en la Figura\(\PageIndex{12}\) incluye una fuente de voltaje\(E(t)\),, que agrega voltaje al circuito, tenemos\(E_L+E_R+E_C=E(t)\).

Presentamos las fórmulas a continuación sin mayor desarrollo y aquellos de ustedes interesados en la derivación de estas fórmulas pueden revisar los enlaces. Usando la ley de Faraday y la ley de Lenz, se puede demostrar que la caída de voltaje a través de un inductor es proporcional a la tasa instantánea de cambio de corriente, con constante de proporcionalidad\(L.\) Así,

\[E_L=L\dfrac{dI}{dt}. \nonumber \]

A continuación, según la ley de Ohm, la caída de voltaje a través de una resistencia es proporcional a la corriente que pasa a través de la resistencia, con constante de proporcionalidad\(R.\) Por lo tanto,

\[E_R=RI. \nonumber \]

Por último, la caída de voltaje a través de un condensador es proporcional a la carga,\(q,\) en el condensador, con constante de proporcionalidad\(1/C\). Así,

\[E_C=\dfrac{1}{C}q. \nonumber \]

Agregando estos términos juntos, obtenemos

\[L\dfrac{dI}{dt}+RI+\dfrac{1}{C}q=E(t). \nonumber \]

Señalando que\(I=(dq)/(dt)\), esto se convierte en

\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t). \nonumber \]

Matemáticamente, este sistema es análogo a los sistemas de masa-resorte que hemos estado examinando en esta sección.

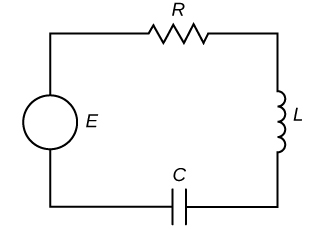
Esta figura es un diagrama de un circuito. Tiene líneas discontinuas en la parte inferior etiquetada C. En el lado izquierdo hay un círculo abierto etiquetado E. La parte superior tiene líneas diagonales etiquetadas R. El lado derecho tiene pequeñas protuberancias etiquetadas L. — Figura\(\PageIndex{12}\): Un circuito en serie *RLC* se puede modelar mediante la misma ecuación diferencial que un sistema masa-resorte.

Circuito en serie

Encuentre la carga en el condensador en un circuito serie RLC donde\(L=5/3\) H,\(R=10Ω\),\(C=1/30\) F y\(E(t)=300\) V. Suponga que la carga inicial en el condensador es de 0 C y la corriente inicial es de 9 A. ¿Qué sucede con la carga en el condensador a lo largo del tiempo?

Solución

Tenemos

\[\begin{align*} L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q &=E(t) \\[4pt] \dfrac{5}{3} \dfrac{d^2q}{dt^2}+10\dfrac{dq}{dt}+30q &=300 \\[4pt] \dfrac{d^2q}{dt^2}+6\dfrac{dq}{dt}+18q &=180. \end{align*}\]

La solución general a la ecuación complementaria es

\[e^{−3t}(c_1 \cos (3t)+c_2 \sin (3t)). \nonumber \]

Asumir una solución particular de la forma\(q_p=A\), donde\(A\) es una constante. Utilizando el método de coeficientes indeterminados, encontramos\(A=10\). Entonces,

\[q(t)=e^{−3t}(c_1 \cos (3t)+c_2 \sin (3t))+10. \nonumber \]

Aplicando las condiciones iniciales\(q(0)=0\) y\(i(0)=((dq)/(dt))(0)=9,\) nos encontramos\(c_1=−10\) y\(c_2=−7.\) Entonces la carga en el condensador es

\[q(t)=−10e^{−3t} \cos (3t)−7e^{−3t} \sin (3t)+10. \nonumber \]

Al observar de cerca esta función, vemos que los dos primeros términos disminuirán con el tiempo (como resultado del exponente negativo en la función exponencial). Por lo tanto, el condensador finalmente se acerca a una carga de estado estacionario de 10 C.

Ejercicio\(\PageIndex{7}\)

Encuentre la carga en el condensador en un circuito serie RLC donde\(L=1/5\) H,\(R=2/5Ω,\)\(C=1/2\) F y\(E(t)=50\) V. Suponga que la carga inicial en el condensador es de 0 C y la corriente inicial es de 4 A.

Pista: Recuerda,\(E_L=L((dI)/(dt)).\)

Contestar: \[q(t)=−25e^{−t} \cos (3t)−7e^{−t} \sin (3t)+25 \nonumber \]

Conceptos clave

Las ecuaciones diferenciales de coeficiente constante de segundo orden se pueden utilizar para modelar sistemas de masa elástica.
Un examen de las fuerzas en un sistema de masa-resorte da como resultado una ecuación diferencial de la forma\[mx″+bx′+kx=f(t), \nonumber \] donde mm representa la masa, bb es el coeficiente de la fuerza de amortiguación,\(k\) es la constante elástica y\(f(t)\) representa cualquier fuerza externa neta en el sistema.
Si\(b=0\), no hay una fuerza de amortiguación que actúe sobre el sistema, y se obtiene un movimiento armónico simple.
Si\(b≠0\), el comportamiento del sistema depende de si\(b^2−4mk>0, b^2−4mk=0,\) o\(b^2−4mk<0.\)
- Si\(b^2−4mk>0,\) el sistema está sobreamortiguado y no presenta comportamiento oscilatorio.
- Si\(b^2−4mk=0,\) el sistema está amortiguado críticamente. No presenta comportamiento oscilatorio, pero cualquier ligera reducción en la amortiguación daría como resultado un comportamiento oscilatorio.
- Si\(b^2−4mk<0\), el sistema está subamortiguado. Presenta un comportamiento oscilatorio, pero la amplitud de las oscilaciones disminuye con el tiempo.
Si\(f(t)≠0\), la solución a la ecuación diferencial es la suma de una solución transitoria y una solución de estado estacionario. La solución de estado estacionario gobierna el comportamiento a largo plazo del sistema.
La carga en el condensador en un circuito en serie RLC también se puede modelar con una ecuación diferencial de coeficiente constante de segundo orden de la forma\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t), \nonumber \] donde\(L\) está la inductancia,\(R\) es la resistencia,\(C\) es la capacitancia y\(E(t)\) es la fuente de voltaje.

Ecuaciones Clave

Ecuación del movimiento armónico simple\[x″+ω^2x=0 \nonumber \]
Solución para un movimiento armónico simple\[x(t)=c_1 \cos (ωt)+c_2 \sin (ωt) \nonumber \]
Forma alternativa de solución para SHM\[x(t)=A \sin (ωt+ϕ) \nonumber \]
Movimiento armónico forzado\[mx″+bx′+kx=f(t)\nonumber \]
Carga en un circuito de la serie RLC\[L\dfrac{d^2q}{dt^2}+R\dfrac{dq}{dt}+\dfrac{1}{C}q=E(t),\nonumber \]

Glosario

Circuito de la serie RLC: una trayectoria eléctrica completa que consiste en una resistencia, un inductor y un condensador; se puede usar una ecuación diferencial de coeficiente constante de segundo orden para modelar la carga en el condensador en un circuito en serie RLC

movimiento armónico simple: movimiento descrito por la ecuación\(x(t)=c_1 \cos (ωt)+c_2 \sin (ωt)\), tal como lo exhibe un sistema de masa elástica no amortiguada en el que la masa continúa oscilando indefinidamente

solución de estado estacionario: una solución a una ecuación diferencial no homogénea relacionada con la función de forzamiento; a largo plazo, la solución se aproxima a la solución de estado estacionario