1.5: Líneas y Planos

Ahora que sabemos cómo realizar algunas operaciones sobre vectores, podemos empezar a tratar con algunos objetos geométricos familiares, como líneas y planos, en el lenguaje de los vectores. La razón para hacerlo es simple: el uso de vectores facilita el estudio de objetos en el espacio euclidiano tridimensional. Primero consideraremos líneas.

Línea a través de un punto, paralela a un vector

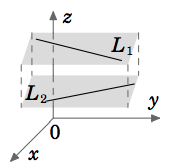
Let\(P=(x_0,y_0,z_0)\) be a point in\(R3\), let\(v=(a,b,c)\) be a nonzero vector, y let\(L\) be the line through\(P\) which is parallel to\(v\) (ver Figura 1.5.1).

Figura 1.5.1

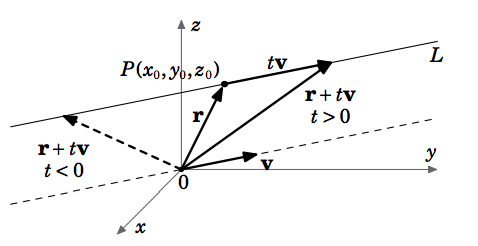
Dejar\(\textbf{r}=(x_0,y_0,z_0)\) ser el vector apuntando desde el origen a P. Ya que multiplicar el vector\(\textbf{v}\) por un escalar\(t\) alarga o encoge\(\textbf{v}\) conservando su dirección si\(t>0\), e invirtiendo su dirección si\(t<0\), entonces vemos en la Figura 1.5.1 que cada punto de la línea \(L\)se puede obtener añadiendo el vector\(t \textbf{v}\) al vector\(\textbf{r}\) para algún escalar\(t\). Es decir, como\(t\) varía sobre todos los números reales, el vector\(\textbf{r} + t \textbf{v}\) apuntará a cada punto encendido\(L\). Podemos resumir el\(\textit{vector representation of \(L\)}\) de la siguiente manera:

Para un punto\(P = (x_{0}, y_{0}, z_{0})\) y un vector distinto de cero\(\textbf{v}\) en\(\mathbb{R}^{3}\), la línea\(L\) a través del\(P\) paralelo a\(\textbf{v}\) viene dada por

\[\textbf{r} + t \textbf{v}, \text{for} -\infty < t < \infty \label{Eq1.16}\]

donde\(\textbf{r} = (x_{0}, y_{0}, z_{0})\) está el vector apuntando a\(P\).

Tenga en cuenta que se utilizó la correspondencia entre un vector y su punto terminal. Desde\(\textbf{v} = (a,b,c)\) entonces el punto terminal del vector\(\textbf{r} + t \textbf{v}\) es\((x_{0} + at, y_{0} + bt, z_{0} + ct)\). Luego conseguimos el\(\textit{parametric representation of L}\) con el\(\textit{parameter}\)\(t\):

Para un punto\(P = (x_{0}, y_{0}, z_{0})\) y un vector distinto de cero\(\textbf{v} = (a,b,c)\) en\(\mathbb{R}^{3}\), la línea\(L\) a través del\(P\) paralelo a\(\textbf{v}\) consiste en todos los puntos\((x,y,z)\) dados por

\[x = x_{0} + at,\quad y = y_{0} + bt,\quad z = z_{0} + ct, \text{for} -\infty < t < \infty \label{Eq1.17}\]

Tenga en cuenta que en ambas representaciones obtenemos\(P\) el punto\(L\) al dejar\(t = 0\).

En Ecuación\ ref {Eq1.17}, si\(a \ne 0\), entonces podemos resolver para el parámetro\(t\):\(t = (x - x_{0})/a\). También podemos resolver para\(t\) en términos de\(y\) y en términos de\(z\) si ni\(b\) ni\(c\), respectivamente, es cero:\(t = (y - y_{0})/b\) y\(t = (z - z_{0})/c\). Estos tres valores son todos iguales al mismo valor\(t\), por lo que podemos escribir el siguiente sistema de igualdades, llamado el\(\textit{symmetric representation of L}\):

Para un punto\(P = (x_{0}, y_{0}, z_{0})\) y vector\(\textbf{v} = (a,b,c)\) en\(\mathbb{R}^{3}\) con\(a\),\(b\) y\(c\) todo distinto de cero, la línea\(L\) a través del\(P\) paralelo a\(\textbf{v}\) consiste en todos los puntos\((x,y,z)\) dados por las ecuaciones

\[\frac{x - x_{0}}{a} = \frac{y - y_{0}}{b} = \frac{z - z_{0}}{c}\]

Figura 1.5.2

Habrás notado que la representación vectorial de\(L\) en Ecuación\ ref {Eq1.16} es más compacta que las fórmulas paramétricas y simétricas. Esa es una ventaja de usar la notación vectorial. Técnicamente, sin embargo, la representación vectorial nos da los\(\textit{vectors}\) cuyos puntos terminales conforman la línea\(L\), no solo\(L\) en sí misma. Entonces hay que recordar identificar los vectores\(\textbf{r} + t \textbf{v}\) con sus puntos terminales. Por otro lado, la representación paramétrica\(\textit{always}\) da solo los puntos encendidos\(L\) y nada más.

Solución

(a) Dejar\(\textbf{r} = (2,3,5)\). Entonces por Ecuación\ ref {Eq1.16},\(L\) viene dada por:\[\nonumber \textbf{r} + t \textbf{v} = (2,3,5) + t(4,-1,6), \text{for} -\infty < t < \infty\]

b)\(L\) Consiste en los puntos de\((x,y,z)\) tal manera que\[\nonumber x = 2 + 4t, y = 3 - t, z = 5 + 6t, \text{for} -\infty < t < \infty\]

c)\(L\) Consiste en los puntos de\((x,y,z)\) tal manera que\[\nonumber \frac{x - 2}{4} = \frac{y - 3}{-1} = \frac{z - 5}{6}\]

d) El dejar\(t=1\) y\(t=2\) en parte (b) arroja los puntos\((6,2,11)\) y\((10,1,17)\) sucesivamente\(L\).

Línea a través de dos puntos

La Figura 1.5.3,\(\textbf{r}_{2} - \textbf{r}_{1}\) es el vector de\(P_{1}\) a\(P_{2}\). Entonces, si multiplicamos el vector\(\textbf{r}_{2} - \textbf{r}_{1}\) por un escalar\(t\) y lo agregamos al vector\(\textbf{r}_{1}\), obtendremos toda la línea\(L\) ya que\(t\) varía sobre todos los números reales. El siguiente es un resumen de las formas vectoriales, paramétricas y simétricas para la línea\(L\):

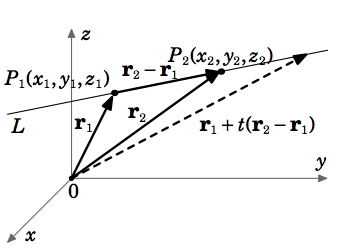
Dejar\(P_{1} = (x_{1}, y_{1}, z_{1})\),\(P_{2} = (x_{2}, y_{2}, z_{2})\) ser puntos distintos en\(\mathbb{R}^{3}\), y dejar\(\textbf{r}_{1} = (x_{1}, y_{1}, z_{1})\),\(\textbf{r}_{2} = (x_{2}, y_{2}, z_{2})\). Luego la línea\(L\) a través\(P_{1}\) y\(P_{2}\) tiene las siguientes representaciones:

\(\textit{Vector:}\)\[\textbf{r}_{1} + t(\textbf{r}_{2} - \textbf{r}_{1}) \text{, for} -\infty < t < \infty\]

\(\textit{Parametric:}\)\[x = x_{1} + (x_{2} - x_{1})t, y = y_{1} + (y_{2} - y_{1})t, z = z_{1} + (z_{2} - z_{1})t, \text{for} -\infty < t < \infty \label{Eq1.21}\]

\(\textit{Symmetric:}\)\[\frac{x - x_{1}}{x_{2} - x_{1}} = \frac{y - y_{1}}{y_{2} - y_{1}} = \frac{z - z_{1}}{z_{2} - z_{1}} \text{if \(x_{1} \ne x_{2}\), \(y_{1} \ne y_{2}\), and \(z_{1} \ne z_{2}\)}\]

Solución

Por Ecuación\ ref {Eq1.21},\(L\) consiste en los puntos\((x,y,z)\) tales que\[\nonumber x = -3 + 7t, y = 1 +3t, z = -4 -2t, \text{for} -\infty < t < \infty\]

Distancia entre un punto y una línea

Figura 1.5.4). Escoge un punto\(Q\) en\(L\), y deja\(\textbf{w}\) ser el vector de\(Q\) a\(P\). Si\(\theta\) es el ángulo entre\(\textbf{w}\) y\(\textbf{v}\), entonces\(d = \norm{\textbf{w}}\,\sin \theta\). Entonces desde\(\norm{\textbf{v} \times \textbf{w}} = \norm{\textbf{v}}\,\norm{\textbf{w}}\,\sin \theta\) y\(\textbf{v} \ne \textbf{0}\), entonces:

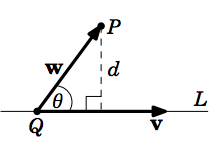
\[d = \frac{\norm{\textbf{v} \times \textbf{w}}}{\norm{\textbf{v}}}\]

Encuentra la distancia\(d\) from the point \(P = (1,1,1)\) to the line \(L\) in Example 1.20.

Solución

Del Ejemplo 1.20, vemos que podemos representar\(L\) en forma vectorial como:\(\textbf{r} + t \textbf{v}\), for\(\textbf{r} = (-3,1,-4)\) y\(\textbf{v} = (7,3,-2)\). Ya que el punto\(Q = (-3,1,-4)\) está encendido\(L\), entonces para\(\textbf{w} = \overrightarrow{QP} = (1,1,1) - (-3,1,-4) = (4,0,5)\), tenemos:

\ [\ nonumber\ textbf {v}\ times\ textbf {w} =\ izquierda|\ begin {array} {rrr}\ textbf {i} &\ textbf {j} &\ textbf {k}\\ [4pt] 7 & 3 y -2\\ [4pt]
4 & 0 & 5\ end {array}\ derecha|
=\ izquierda|\ begin {array} {rr} 3 & -2\\ [4pt] 0 & 5\ end {array}\ derecha|\ textbf {i}\; -\;
\ izquierda|\ begin {array} {rr} 7 y -2\\ [4pt] 4 & 5\ end {array}\ derecha|\ textbf {j}\; +\;
\ izquierda|\ begin {array} {rr} 7 & 3\\ [4pt] 4 & 0\ end {array}\ derecha|\ textbf {k}
= 15\,\ textbf {i} - 43\,\ textbf {j} - 12\,\ textbf {k}\ texto {, entonces}\\ [4pt]\ nonúmero
d =\ frac {\ norm {\ textbf {v} \ times\ textbf {w}}} {\ norm {\ textbf {v}}} =
\ frac {\ norm {15\,\ textbf {i} - 43\,\ textbf {j} - 12\,\ textbf {k}}} {\ norm {(7,3, -2)}}
=\ frac {\ sqrt {15^ {2} + (-43) ^ {2} + (-12) ^ {2}}} {\ sqrt {7^ {2} + 3^ {2} + (-2) ^ {2}}}
=\ frac {\ sqrt {2218}} {\ sqrt {62}} = 5.98\]

Figura 1.5.5).

Para determinar si dos líneas se\(\mathbb{R}^{3}\) cruzan, a menudo es más fácil usar la representación paramétrica de las líneas. En este caso, se deben usar diferentes variables de parámetros (generalmente\(s\) y\(t\)) para las líneas, ya que los valores de los parámetros pueden no ser los mismos en el punto de intersección. Establecer las dos\((x,y,z)\) triples iguales dará como resultado un sistema de 3 ecuaciones en 2 incógnitas (\(s\)y\(t\)).

Ejemplo 1.22

Encuentre el punto de intersección (si lo hay) de las siguientes líneas:\[\nonumber \frac{x + 1}{3} = \frac{y - 2}{2} = \frac{z - 1}{-1} \text{ and } x + 3 = \frac{y - 8}{-3} = \frac{z + 3}{2}\]

Solución

Primero escribimos las líneas en forma paramétrica, con parámetros\(s\) y\(t\):

\[\nonumber x = -1 + 3s, y = 2 + 2s, z = 1 - s \text{ and } x = -3 + t, y = 8 - 3t, z = -3 + 2t\]

Las líneas se cruzan cuando\((-1 + 3s,2 + 2s,1 - s) = (-3 + t,8 - 3t,-3 + 2t)\) para algunos\(s\),\(t\):

\ begin {alinear*}
\ nonumber -1 + 3s = -3 + t &:\ Rightarrow t = 2 + 3s\\ [4pt]\ nonumber
2 + 2s = 8 - 3t &:\ Rightarrow 2 + 2s = 8 - 3 (2 + 3s) = 2 - 9s\ Rightarrow 2s = -9s\ Rightarrow s = 0\ Rightarrow t = 2 + 3 (0) = 2\\ [4pt]\ nonumber
1 - s = -3 + 2t &: 1 - 0 = -3 + 2 (2)\ Rightarrow 1 = 1\ checkmark\ text {(Tenga en cuenta que tuvimos que verificar esto.)}
\ end {align*}

Dejar\(s = 0\) entrar las ecuaciones para la primera línea, o dejar\(t = 2\) entrar las ecuaciones para la segunda línea, da el punto de intersección\((-1,2,1)\).

Figura 1.5.6 El plano\(P\)

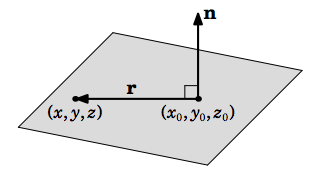
Por el contrario, si\((x,y,z)\) hay algún punto en\(\mathbb{R}^{3}\) tal que\(\textbf{r} = (x - x_{0}, y - y_{0}, z - z_{0}) \ne \textbf{0}\) y\(\textbf{n} \cdot \textbf{r} = 0\), entonces\(\textbf{r} \perp \textbf{n}\) y así\((x,y,z)\) yace en\(P\). Esto demuestra el siguiente teorema:

Teorema 1.18

Dejar\(P\) ser un plano en\(\mathbb{R}^{3}\), dejar\((x_{0}, y_{0}, z_{0})\) ser un punto en\(P\), y dejar\(\textbf{n} = (a,b,c)\) ser un vector distinto de cero que es perpendicular a\(P\). Luego\(P\) consiste en los puntos\((x,y,z)\) que satisfacen la ecuación vectorial:

\[\textbf{n} \cdot \textbf{r} = 0\]

donde\(\textbf{r} = (x - x_{0}, y - y_{0}, z - z_{0})\), o equivalentemente:

\[a(x - x_{0}) + b(y - y_{0}) + c(z - z_{0}) = 0 \label{Eq1.25}\]

La ecuación anterior se llama la\(\textbf{point-normal form}\) del plano\(P\).

Solución

Por Ecuación\ ref {Eq1.25}, el plano\(P\) consta de todos los puntos\((x,y,z)\) tales que:
\[\nonumber 2(x + 3) + 4(y - 1) + 8(z - 3) = 0 \]

Figura 1.5.7: Puntos no colineales\(Q, R, S\)

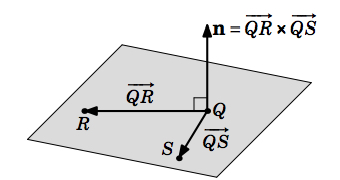
Solución

Vamos\(Q = (2,1,3)\),\(R = (1,-1,2)\) y\(S = (3,2,1)\). Luego para los vectores\(\overrightarrow{QR} = (-1,-2,-1)\) y\(\overrightarrow{QS} = (1,1,-2)\), el plano\(P\) tiene un vector normal

\[\nonumber \textbf{n} = \overrightarrow{QR} \times \overrightarrow{QS} = (-1,-2,-1) \times (1,1,-2) = (5,-3,1)\]

Entonces usando la Ecuación\ ref {Eq1.25} con el punto\(Q\) (también podríamos usar\(R\) o\(S\)), el plano\(P\) consiste en todos los puntos\((x,y,z)\) tales que:

\[\nonumber 5(x - 2) - 3(y - 1) + (z - 3) = 0\]

o en forma normal,

\[\nonumber 5x - 3y + z - 10 = 0\]

Mencionamos anteriormente que las líneas sesgadas\(\mathbb{R}^{3}\) se encuentran en planos separados, paralelos. Por lo que dos líneas sesgadas no determinan un plano. Pero dos líneas (no idénticas) que se cruzan o son paralelas determinan un plano. En ambos casos, para encontrar la ecuación del plano que contiene esas dos líneas, simplemente elija de las dos líneas un total de tres puntos no colineales (es decir, un punto de una línea y dos puntos de la otra), luego use la técnica anterior, como en el Ejemplo 1.24, para escribir la ecuación. Dejaremos ejemplos de esto como ejercicios para el lector.

Distancia entre un punto y un plano

La distancia entre un punto en\(\mathbb{R}^{3}\) y un plano es la longitud del segmento de línea desde ese punto hasta el plano que es perpendicular al plano. El siguiente teorema da una fórmula para esa distancia.

Teorema 1.19

Dejar\(Q = (x_{0}, y_{0}, z_{0})\) ser un punto en\(\mathbb{R}^{3}\), y dejar\(P\) ser un plano con forma normal\(ax + by + cz + d = 0\) que no contiene\(Q\). Entonces la distancia\(D\) de\(Q\) a\(P\) es:

\[D = \frac{|ax_{0} + by_{0} + cz_{0} + d|}{\sqrt{a^{2} + b^{2} + c^{2}}}\]

Figura 1.5.8

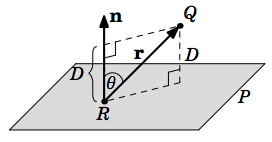
Por Teorema 1.6 en la Sección 1.3, sabemos que\(\cos \theta = \dfrac{\textbf{n} \cdot \textbf{r}}{\norm{\textbf{n}} \norm{\textbf{r}}}\), entonces

\[\nonumber \begin{align}D &= |\cos \theta|\,\norm{\textbf{r}}= \dfrac{|\textbf{n} \cdot \textbf{r}|}{\norm{\textbf{n}} \norm{\textbf{r}}}\,\norm{\textbf{r}}= \dfrac{|\textbf{n} \cdot \textbf{r}|}{\norm{\textbf{n}}}= \dfrac{|a(x_{0} - x) + b(y_{0} - y) + c(z_{0} - z)|}{\sqrt{a^{2} + b^{2} + c^{2}}} \\[4pt] \nonumber &= \dfrac{ax_{0} + by_{0} + cz_{0} - (ax + by + cz)}{\sqrt{a^{2} + b^{2} + c^{2}}}= \dfrac{|ax_{0} + by_{0} + cz_{0} - (-d)|}{\sqrt{a^{2} + b^{2} + c^{2}}}= \dfrac{|ax_{0} + by_{0} + cz_{0} + d|}{\sqrt{a^{2} + b^{2} + c^{2}}} \\[4pt] \end{align}\]

Si\(\textbf{n}\) apunta lejos del lado de\(P\) donde\(Q\) se encuentra el punto, entonces\(90^{\circ} < \theta < 180^{\circ}\) y así\(\cos \theta < 0\). La distancia\(D\) es entonces\(|\cos \theta| \, \norm{\textbf{r}}\), y repitiendo así el mismo argumento que el anterior sigue dando el mismo resultado.

\[\nonumber D = \frac{|5(2) - 3(4) + 1(-5) - 10|}{\sqrt{5^{2} + (-3)^{2} + 1^{2}}} = \frac{|-17|}{\sqrt{35}} = \frac{17}{\sqrt{35}} \approx 2.87\]

Línea de intersección de dos planos

Figura 1.5.9: Supongamos que dos planos\(P_{1}\) y\(P_{2}\) con vectores normales\(\textbf{n}_{1}\) y\(\textbf{n}_{2}\), respectivamente, se cruzan en una línea\(L\). Ya que\(\textbf{n}_{1} \times \textbf{n}_{2} \perp \textbf{n}_{1}\), entonces\(\textbf{n}_{1} \times \textbf{n}_{2}\) es paralelo al plano\(P_{1}\). De igual manera,\(\textbf{n}_{1} \times \textbf{n}_{2} \perp \textbf{n}_{2}\) significa que también\(\textbf{n}_{1} \times \textbf{n}_{2}\) es paralelo a\(P_{2}\). Por lo tanto,\(\textbf{n}_{1} \times \textbf{n}_{2}\) es paralelo a la intersección de\(P_{1}\) y\(P_{2}\), es decir,\(\textbf{n}_{1} \times \textbf{n}_{2}\) es paralelo a\(L\). Así, podemos escribir\(L\) en la siguiente forma vectorial:

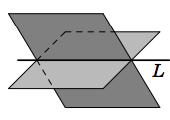
\[L: \textbf{r} + t(\textbf{n}_{1} \times \textbf{n}_{2}) \text{, for} -\infty < t < \infty\]

donde\(\textbf{r}\) es cualquier vector que apunte a un punto perteneciente a ambos planos. Para encontrar un punto en ambos planos, encontrar una solución común\((x,y,z)\) a las dos ecuaciones de forma normal de los planos. Esto a menudo se puede hacer más fácil estableciendo una de las variables de coordenadas en cero, lo que te deja resolver dos ecuaciones en solo dos incógnitas.

\[\nonumber \begin{align} -&3y + z - 10 = 0 \\[4pt] \nonumber &4y - z + 3 = 0 \\[4pt] \end{align}\]

La segunda ecuación da\(z = 4y + 3\), sustituyendo eso en la primera ecuación da\(y = 7\). Entonces\(z = 31\), y así el punto\((0,7,31)\) está encendido\(L\). Ya que\(\textbf{n}_{1} \times \textbf{n}_{2} = (-1,7,26)\), entonces\(L\) viene dado por:

\[\nonumber \textbf{r} + t(\textbf{n}_{1} \times \textbf{n}_{2}) = (0,7,31) + t(-1,7,26), \text{for} -\infty < t < \infty\]

o en forma paramétrica:

\[\nonumber x = -t, y = 7 + 7t, z = 31 +26t, \text{for} -\infty < t < \infty\]

Colaboradores y Atribuciones

• Template:ContribCorral