1.6: Superficies
- Page ID
- 111246
En la sección anterior discutimos planos en el espacio euclidiano. Un plano es un ejemplo de a\(\textit{surface}\), que definiremos informalmente como el conjunto de solución de la ecuación\(F(x,y,z) = 0\) en\(\mathbb{R}^{3}\), para alguna función de valor real\(F\). Por ejemplo, un plano dado por\(ax + by + cz + d = 0\) es el conjunto de soluciones de\(F(x,y,z) = 0\) para la función\(F(x,y,z) = ax + by + cz + d\). Las superficies son bidimensionales. El plano es la superficie más simple, ya que es “plana”. En esta sección veremos algunas superficies que son más complejas, las más importantes de las cuales son la esfera y el cilindro.
Definición: Esfera
A\(\textbf{sphere}\)\(S\) es el conjunto de todos los puntos\((x,y,z)\) en los\(\mathbb{R}^{3}\) que se encuentran una distancia fija\(r\) (llamada la\(\textbf{radius}\)) desde un punto fijo\(P_{0} = (x_{0}, y_{0}, z_{0})\) (llamado el\(\textbf{center}\) de la esfera):
\[S = \lbrace \, (x,y,z): \, (x - x_{0})^{2} + (y - y_{0})^{2} + (z - z_{0})^{2} = r^{2} \, \rbrace \label{Eq1.29}\]
Usando notación vectorial, esto se puede escribir en la forma equivalente:
\[S = \lbrace \, \textbf{x}: \, \norm{\textbf{x} - \textbf{x}_{0}} = r \, \rbrace\]
donde\(\textbf{x} = (x,y,z)\) y\(\textbf{x}_{0} = (x_{0}, y_{0}, z_{0})\) son vectores.
La figura\(\PageIndex{1}\) ilustra el enfoque vectorial de las esferas.
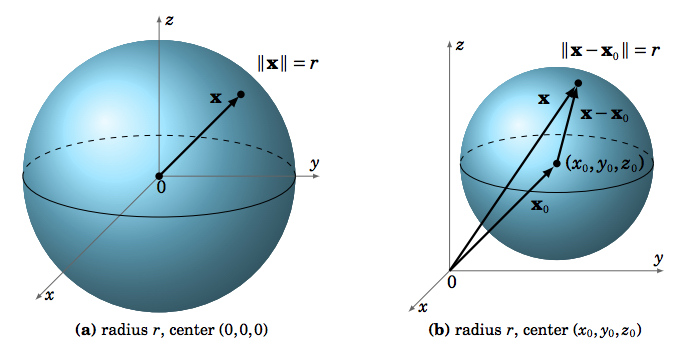
\(\PageIndex{1a}\)Obsérvese en la Figura que la intersección de la esfera con el\(xy\) -plano es un círculo de radio\(r\) (es decir\(\textit{great circle}\), a, dado por\(x^{2} + y^{2} = r^{2}\) como un subconjunto de\(\mathbb{R}^{2}\)). De manera similar para las intersecciones con el\(xz\) plano -plano y el\(yz\) -plano. En general, un plano cruza una esfera ya sea en un solo punto o en un círculo.
Ejemplo\(\PageIndex{1}\): Intersection of a sphere and a plane
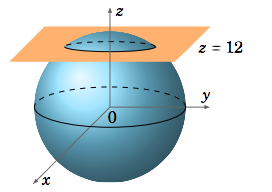
Encuentra la intersección de la esfera\(x^{2} + y^{2} + z^{2} = 169\) con el plano\(z = 12\).
La esfera está centrada en el origen y tiene radio\(13 = \sqrt{169}\), por lo que sí se cruza con el plano\(z = 12\). Poner\(z = 12\) en la ecuación de la esfera da
\[\begin{align*} \nonumber x^{2} + y^{2} + 12^{2} &= 169 \\[4pt] \nonumber x^{2} + y^{2} &= 169 - 144 = 25 = 5^{2} \end{align*}\]
que es un círculo de radio\(5\) centrado en\((0,0,12)\), paralelo al\(xy\) plano (Figura\(\PageIndex{2}\)).
Si la ecuación en la Ecuación\ ref {Eq1.29} se multiplica, obtenemos una ecuación de la forma:
\[x^{2} + y^{2} + z^{2} + ax + by + cz + d = 0\]
para algunas constantes\(a\),\(b\),\(c\) y\(d\). Por el contrario, una ecuación de esta forma\(\textit{may}\) describe una esfera, que se puede determinar completando el cuadrado para las\(z\) variables\(x\),\(y\) y.
Ejemplo\(\PageIndex{2}\)
¿Es\(2x^{2} + 2y^{2} + 2z^{2} - 8x + 4y - 16z + 10 = 0\) la ecuación de una esfera?
Solución
Dividiendo ambos lados de la ecuación por\(2\) da
\[\nonumber x^{2} + y^{2} + z^{2} - 4x + 2y - 8z + 5 = 0\]
\[\nonumber (x^{2} - 4x + 4) + (y^{2} + 2y + 1) + (z^{2} - 8z + 16) + 5 - 4 - 1 - 16 = 0\]
\[\nonumber (x - 2)^{2} + (y + 1)^{2} + (z - 4)^{2} = 16\]
que es una esfera de radio\(4\) centrada en\((2,-1,4)\).
Ejemplo\(\PageIndex{3}\)
Encuentra los puntos de intersección (si los hay) de la esfera de Ejemplo\(\PageIndex{2}\) y la línea\(x = 3 + t\),\(y = 1 + 2t\),\(z = 3 - t\).
Solución
Poner las ecuaciones de la línea en la ecuación de la esfera, que era\((x - 2)^{2} + (y + 1)^{2} + (z - 4)^{2} = 16\), y resolver para\(t\):
\ begin {alinear*}
\ nonumber (3 + t - 2) ^ {2} + (1 + 2t + 1) ^ {2} + (3 - t - 4) ^ {2} &= 16\\ [4pt]
\ nonúmero (t + 1) ^ {2} + (2t + 2) ^ {2} + (-t - 1) ^ {2} &= 16\\ [4pt]
\ nonumber 6t^ {2} + 12t -10 &= 0
\ end {alinear*}
La fórmula cuadrática da las soluciones\(~t = -1 \pm \dfrac{4}{\sqrt{6}}\). Al poner esos dos valores en las ecuaciones de la línea se obtienen los siguientes dos puntos de intersección:
\[\nonumber \left( 2 + \frac{4}{\sqrt{6}}, -1 + \frac{8}{\sqrt{6}}, 4 - \frac{4}{\sqrt{6}} \right) \text{ and } \left( 2 - \frac{4}{\sqrt{6}}, -1 - \frac{8}{\sqrt{6}}, 4 + \frac{4}{\sqrt{6}} \right)\]
Si dos esferas se cruzan, lo hacen ya sea en un solo punto o en un círculo (a menos que sean de tamaño idéntico y no estén desplazadas entre sí).
Ejemplo\(\PageIndex{4}\)
Encuentra la intersección (si la hay) de las esferas\(x^{2} + y^{2} + z^{2} = 25\) y\(x^{2} + y^{2} + (z - 2)^{2} = 16\).
Solución
Para cualquier punto\((x,y,z)\) en ambas esferas, vemos que
\ begin {alinear*}
\ nonumber x^ {2} + y^ {2} + z^ {2} = 25 &\ Rightarrow x^ {2} + y^ {2} = 25 - z^ {2},\ text {y}\\ [4pt]
\ nonumber x^ {2} + y^ {2} + (z - 2) ^ {2} = 16 &\ Fila derecha x^ {2} + y^ {2} = 16 - (z - 2) ^ {2},\ text {so}\\\ [4pt]
\ nonumber 16 - (z - 2) ^ {2} = 25 - z ^ {2} &\ Fila derecha 4z - 4 = 9\ Rightarrow z = 13/4\\ [4pt]
\ nonumber &\ Rightarrow x^ {2} + y^ {2} = 25 - (13/4) ^ {2} = 231/16
\ end {align*}
\(\therefore\)La intersección es el círculo\(x^{2} + y^{2} = \frac{231}{16}\) de radio\(\frac{\sqrt{231}}{4} \approx 3.8\) centrado en\((0,0,\frac{13}{4})\).
Los cilindros que consideraremos son\(\textit{right circular cylinders}\). Se trata de cilindros que se obtienen moviendo una línea\(L\) a lo largo\(C\) de\(\mathbb{R}^{3}\) un círculo de una manera que siempre\(L\) sea perpendicular al plano que lo contiene\(C\). Solo consideraremos los casos en los que el plano que contiene\(C\) es paralelo a uno de los tres planos de coordenadas (Figura\(\PageIndex{3}\)).
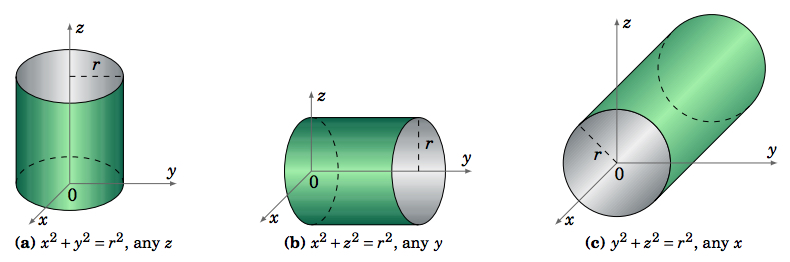
Por ejemplo, la ecuación de un cilindro cuyo círculo base\(C\) se encuentra en el\(xy\) plano y está centrado en\((a,b,0)\) y tiene radio\(r\) es
\ begin {ecuación}\ label {eqn:cylxy}
(x - a) ^2 + (y - b) ^2 = r^2,
\ end {ecuación}
donde el valor de la\(z\) coordenada no está restringido. Ecuaciones similares se pueden escribir cuando el círculo base se encuentra en uno de los otros planos de coordenadas. Un plano cruza un cilindro circular derecho en un círculo, elipse o una o dos líneas, dependiendo de si ese plano es paralelo, oblicuo o perpendicular, respectivamente, al plano que lo contiene\(C\). La intersección de una superficie con un plano se llama la\(\textbf{trace}\) de la superficie.
Las ecuaciones de esferas y cilindros son ejemplos de ecuaciones de segundo grado en\(\mathbb{R}^ 3\), es decir, ecuaciones de la forma
\ begin {ecuación}\ label {Eq1.33}
Ax^2 + By^2 + Cz^2 + Dxy + Exz + Fyz + Gx + Hy + Iz + J = 0
\ end {ecuación}
para algunas constantes\(A, B, \dots, J\). Si la ecuación anterior no es la de una esfera, cilindro, plano, línea o punto, entonces la superficie resultante se denomina superficie cuádrica.
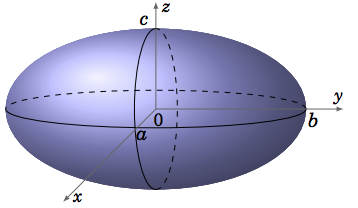
Un tipo de superficie cuádrica es la\(\textbf{ellipsoid}\), dada por una ecuación de la forma:
\ begin {ecuación}\ label {eqn:elipsoide}
\ frac {x^2} {a^2} +\ frac {y^2} {b^2} +\ frac {z^2} {c^2} = 1
\ end {ecuación}
En el caso donde\(a = b = c\), esto es sólo una esfera. En general, un elipsoide tiene forma de huevo (piense en una elipse girada alrededor de su eje mayor). Sus trazas en los planos de coordenadas son elipses.
Otros dos tipos de superficies cuádricas son las\(\textbf{hyperboloid of one sheet}\), dadas por una ecuación de la forma:
\ begin {ecuación}\ label {eqn:hiperboloidona}
\ frac {x^2} {a^2} +\ frac {y^2} {b^2} -\ frac {z^2} {c^2} = 1
\ end {ecuación}
y el\(\textbf{hyperboloid of two sheets}\), cuya ecuación tiene la forma:
\ begin {ecuación}\ label {eqn:hyperboloidtwo}
\ frac {x^2} {a^2} -\ frac {y^2} {b^2} -\ frac {z^2} {c^2} = 1
\ end {ecuación}
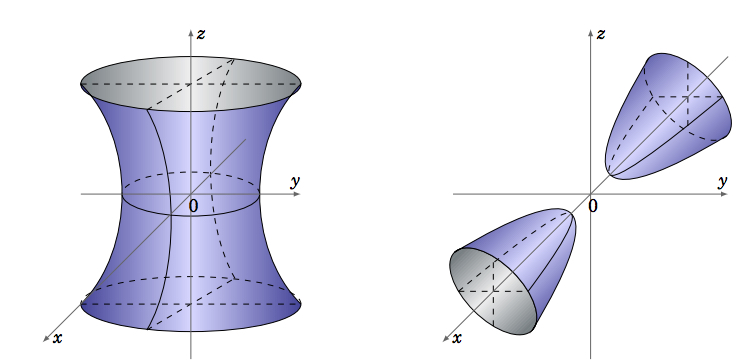
Para el hiperboloide de una hoja, la traza en cualquier plano paralelo al\(xy\) plano -es una elipse. Los trazos en los planos paralelos a los planos\(xz\) - o\(yz\) -planos son hipérbolas (Figura\(\PageIndex{5}\)), a excepción de los casos especiales\(x = \pm a\) y\(y = \pm b\); en esos planos los trazos son pares de líneas que se cruzan (ver Ejercicio 8).
Para el hiperboloide de dos hojas, la traza en cualquier plano paralelo al plano\(xy\) - o\(xz\) -plano es una hipérbola (Figura\(\PageIndex{6}\)). No hay rastro en el\(yz\) -avión. En cualquier plano paralelo al\(yz\) plano -para el cual\(\lvert x \rvert > \lvert a \rvert \), la traza es una elipse.
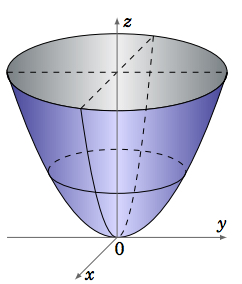
El\(\textbf{elliptic paraboloid}\) es otro tipo de superficie cuádrica, cuya ecuación tiene la forma:
\ begin {ecuación}\ label {eqn:paraboloide}
\ frac {x^2} {a^2} +\ frac {y^2} {b^2} =\ frac {z} {c}
\ end {ecuación}
Las trazas en planos paralelos al\(xy\) plano son elipses, aunque en el\(xy\) plano mismo la traza es un solo punto. Las huellas en planos paralelos a los\(xz\) -o\(yz\) -planos son parábolas. La figura\(\PageIndex{7}\) muestra el caso donde\(c > 0\). Cuando\(c < 0\) la superficie está girada hacia abajo. En el caso donde\(a = b\), la superficie se llama paraboloide de revolución, que a menudo se usa como superficie reflectante, por ejemplo, en los faros de los vehículos.
Una superficie cuádrica más complicada es la\(\textbf{hyperbolic paraboloid}\), dada por:
\[\dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = \dfrac{z}{c}\label{Eq1.38}\]
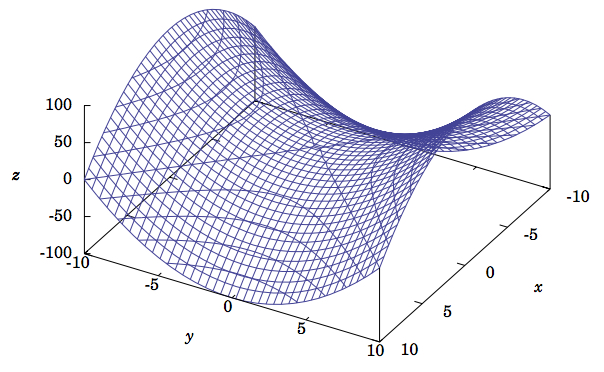
El paraboloide hiperbólico puede ser complicado de dibujar; usar software de gráficos en una computadora puede hacerlo más fácil. Por ejemplo, la Figura\(\PageIndex{8}\) se creó usando el paquete gratuito Gnuplot (ver Apéndice C). Se muestra la gráfica del paraboloide hiperbólico\(z = y^2 - x^2\), que es el caso especial donde\(a = b = 1\) y\(c = -1\) en la Ecuación\ ref {Eq1.38}. Las líneas de malla en la superficie son las trazas en planos paralelos a los planos de coordenadas. Entonces vemos que las huellas en planos paralelos al\(xz\) plano son parábolas apuntando hacia arriba, mientras que las trazas en planos paralelos al\(yz\) plano son parábolas apuntando hacia abajo. Además, observe que las trazas en planos paralelos al\(xy\) plano son hipérbolas, aunque en el\(xy\) plano mismo la traza es un par de líneas que se cruzan a través del origen. Esto es cierto en general cuando\(c < 0\) en la Ecuación\ ref {Eq1.38}. Cuando\(c > 0\), la superficie sería similar a la de la Figura\(\PageIndex{8}\), solo giraba\(90^\circ \) alrededor del\(z\) eje y se invertiría la naturaleza de las trazas en planos paralelos a los\(yz\) planos\(xz\) - o -planos.
El último tipo de superficie cuádrica que consideraremos es la\(\textbf{elliptic cone}\), que tiene una ecuación de la forma:
\ begin {ecuación}\ label {eqn:elipcone}
\ frac {x^2} {a^2} +\ frac {y^2} {b^2} -\ frac {z^2} {c^2} = 0
\ end {ecuación}
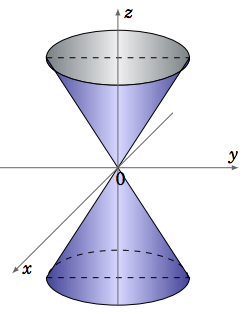
Las trazas en planos paralelos al\(xy\) plano son elipses, excepto en el\(xy\) plano mismo donde la traza es un solo punto. Las trazas en planos paralelos a los planos\(xz\) - o\(yz\) -planos son hipérbolas, excepto en los propios\(yz\) planos\(xz\) - y -donde las trazas son pares de líneas que se cruzan.
Superficie regada
Observe que cada punto del cono elíptico está en una línea que se encuentra completamente en la superficie; en la Figura todas\(\PageIndex{9}\) estas líneas pasan por el origen. Esto hace que el cono elíptico sea un ejemplo de una superficie reglada. El cilindro también es una superficie regada.
Lo que puede no ser tan obvio es que tanto el hiperboloide de una lámina como el paraboloide hiperbólico son superficies regladas. De hecho, en ambas superficies hay dos líneas a través de cada punto de la superficie (Ejercicios 11-12). Tales superficies se llaman superficies doblemente regladas, y los pares de líneas se llaman regular.
Es claro que para cada uno de los seis tipos de superficies cuádricas que discutimos, la superficie se puede traducir lejos del origen (por ejemplo, reemplazando\(x^2\) por\((x - x_0)^2\) en su ecuación). Se puede probar que cada superficie cuádrica puede ser trasladada y/o rotada para que su ecuación coincida con uno de los seis tipos que describimos. Por ejemplo,\(z = 2xy\) es un caso de Ecuación\ ref {Eq1.33} con variables “mixtas”, por ejemplo con\(D \ne 0\) para que obtengamos un\(xy\) término. Esta ecuación no coincide con ninguno de los tipos que consideramos. Sin embargo, al rotar los\(y\) ejes\(x\) -y-\(45^\circ\) en el\(xy\) plano por medio de la transformación de coordenadas\(x = (x' - y')/\sqrt{2}\),,\(y = (x' + y')/\sqrt{2}\)\(z = z'\), luego\(z = 2xy\) se convierte en el paraboloide hiperbólico\(z' = (x')^2 - (y')^2\) en el sistema de\((x',y',z')\) coordenadas. Es decir,\(z = 2xy\) es un paraboloide hiperbólico como en la Ecuación\ ref {Eq1.38}, pero girado\(45^\circ \) en el\(xy\) plano -.


