2.7: Optimización Constreñida - Multiplicadores Lagrange
- Page ID
- 111360
En las Secciones 2.5 y 2.6 nos preocupamos por encontrar máximos y mínimos de funciones sin ninguna restricción sobre las variables (aparte de estar en el dominio de la función). ¿Qué haríamos si hubiera restricciones en las variables? El siguiente ejemplo ilustra un caso sencillo de este tipo de problemas.
Ejemplo 2.24
Para un rectángulo cuyo perímetro sea de 20 m, encuentre las dimensiones que maximizarán el área.
Solución
El área\(A\) de un rectángulo con ancho\(x\) y alto\(y\) es\(A = x y\). El perímetro\(P\) del rectángulo viene dado entonces por la fórmula\(P = 2x+2y\). Ya que se nos da que el perímetro\(P = 20\), este problema se puede afirmar como:
\[\nonumber \begin{align}\text{Maximize : }&f (x, y) = x y \\[4pt] \nonumber \text{given : }&2x+2y = 20 \end{align}\]
El lector probablemente esté familiarizado con un método simple, utilizando cálculo de una sola variable, para resolver este problema. Ya que debemos tener\(2x + 2y = 20\), entonces podemos resolver por, digamos,\(y\) en términos de\(x\) usar esa ecuación. Esto da\(y = 10− x\), que luego sustituimos en\(f\) para obtener\(f (x, y) = x y = x(10 − x) = 10x − x^2\). Esta es ahora una función de\(x\) solo, así que ahora solo tenemos que maximizar la función\(f (x) = 10x− x^2\) en el intervalo [0,10]. Desde\(f ′ (x) = 10−2x = 0 \Rightarrow x = 5 \text{ and }f ′′(5) = −2 < 0\) entonces la Segunda Prueba Derivada nos dice que\(x = 5\) es un máximo local para\(f\), y por lo tanto\(x = 5\) debe ser el máximo global en el intervalo [0,10] (ya que\(f = 0\) en los puntos finales del intervalo). Entonces desde\(y = 10 − x = 5\), entonces el área máxima se da para un rectángulo cuya anchura y altura ambas son de 5 m.
Observe en el ejemplo anterior que la facilidad de la solución dependía de poder resolver para una variable en términos de la otra en la ecuación\(2x+2y = 20\). Pero, ¿y si eso no fuera posible (que suele ser el caso)? En esta sección utilizaremos un método general, llamado método multiplicador Lagrange, para resolver problemas de optimización restringidos:
\[\nonumber \begin{align} \text{Maximize (or minimize) : }&f (x, y)\quad (\text{or }f (x, y, z)) \\[4pt] \nonumber \text{given : }&g(x, y) = c \quad (\text{or }g(x, y, z) = c) \text{ for some constant } c \end{align}\]
La ecuación\(g(x, y) = c\) se llama la ecuación de restricción, y decimos que\(x\) y\(y\) están restringidos por\(g(x, y) = c\). Los puntos\((x, y)\) que son máximos o mínimos\(f (x, y)\) con la condición de que satisfacen la ecuación de restricción\(g(x, y) = c\) se denominan puntos máximos restringidos o mínimos restringidos, respectivamente. Se mantienen definiciones similares para funciones de tres variables.
Ahora se puede afirmar el método multiplicador Lagrange para resolver este tipo de problemas:
Teorema 2.7: El Método Multiplicador de Lagrange
Dejar\(f (x, y)\text{ and }g(x, y)\) ser funciones suaves, y supongamos que\(c\) es una constante escalar tal que\(\nabla g(x, y) \neq \textbf{0}\) para todos los\((x, y)\) que satisfagan la ecuación\(g(x, y) = c\). Luego para resolver el problema de optimización restringida
\[\nonumber \begin{align} \text{Maximize (or minimize) : }&f (x, y) \\[4pt] \nonumber \text{given : }&g(x, y) = c ,\end{align}\]
encontrar los puntos\((x, y)\) que resuelven la ecuación\(\nabla f (x, y) = \lambda \nabla g(x, y)\) para alguna constante\(\lambda\) (el número\(\lambda\) se llama multiplicador de Lagrange). Si hay un máximo o mínimo restringido, entonces debe ser tal punto.
Una prueba rigurosa del teorema anterior requiere el uso del Teorema de la Función Implícita, que está más allá del alcance de este texto. Tenga en cuenta que el teorema sólo da una condición necesaria para que un punto sea un máximo o mínimo restringido. Si un punto\((x, y)\) que satisface\(\nabla f (x, y) = \lambda \nabla g(x, y)\) para algunos\(\lambda\) en realidad es un máximo o mínimo restringido a veces puede ser determinado por la naturaleza del problema en sí. Por ejemplo, en el Ejemplo 2.24 quedó claro que tenía que haber un máximo global.
Entonces, ¿cómo se puede saber cuándo un punto que satisface la condición en el Teorema 2.7 realmente es un máximo o mínimo restringido? La respuesta es que depende de la función de restricción\(g(x, y)\), junto con cualquier restricción implícita. Se puede demostrar que si la ecuación de restricción\(g(x, y) = c\) (más cualquier restricción oculta) describe un conjunto delimitado\(B\) en\(\mathbb{R}^2\), entonces el máximo o mínimo restringido de\(f (x, y)\) ocurrirá ya sea en un punto\((x, y)\) satisfactorio\(\nabla f (x, y) = \lambda \nabla g(x, y)\) o en un punto “límite” del conjunto \(B\).
En el Ejemplo 2.24 la ecuación de restricción\(2x+2y = 20\) describe una línea in\(\mathbb{R}^2\), que por sí misma no está delimitada. Sin embargo, existen restricciones “ocultas”, debido a la naturaleza del problema, es decir\(0 ≤ x, y ≤ 10\), que hacen que esa línea se restrinja a un segmento de línea en\(\mathbb{R}^2\) (incluyendo los puntos finales de ese segmento de línea), que está delimitado.
Ejemplo 2.25
Para un rectángulo cuyo perímetro sea de 20 m, utilice el método multiplicador Lagrange para encontrar las dimensiones que maximizarán el área.
Solución
Como vimos en el Ejemplo 2.24, con\(x\) y\(y\) representando la anchura y la altura, respectivamente, del rectángulo, este problema puede afirmarse como:
\[\nonumber \begin{align} \text{Maximize : }&f (x, y) = x y \\[4pt] \nonumber \text{given : }&g(x, y) = 2x+2y = 20 \end{align}\]
Entonces resolver la ecuación\(\nabla f (x, y) = \lambda \nabla g(x, y)\) para algunos\(\lambda\) significa resolver las ecuaciones\(\dfrac{∂f}{∂x} = \lambda \dfrac{∂g}{∂x}\text{ and }\dfrac{∂f}{∂y} = \lambda \dfrac{∂g}{∂y}\), a saber:
\[\nonumber \begin{align} y &=2\lambda ,\\[4pt] \nonumber x &=2\lambda \end{align}\]
La idea general es resolver para\(\lambda\) en ambas ecuaciones, luego establecer esas expresiones iguales (ya que ambas son iguales\(\lambda\)) para resolver para\(x \text{ and }y\). Haciendo esto obtenemos
\[\nonumber \dfrac{y}{2} = \lambda = \dfrac{x}{2} \Rightarrow x = y ,\]
así que ahora sustituya cualquiera de las expresiones por\(x \text{ or }y\) en la ecuación de restricción para resolver por\(x \text{ and }y\):
\[\nonumber 20 = g(x, y) = 2x+2y = 2x+2x = 4x \quad \Rightarrow \quad x = 5 \quad \Rightarrow \quad y = 5\]
Debe haber un área máxima, ya que el área mínima es 0 y\(f (5,5) = 25 > 0\), por lo tanto, el punto\((5,5)\) que encontramos (llamado punto crítico restringido) debe ser el máximo restringido.
\(\therefore\)El área máxima ocurre para un rectángulo cuyo ancho y alto son ambos de 5 m.
Ejemplo 2.26
Encuentra los puntos en el círculo\(x^2 + y^2 = 80\) que están más cerca y más alejados del punto\((1,2)\).
Solución
La distancia\(d\) de cualquier punto\((x, y)\) al punto\((1,2)\) es
\[\nonumber d = \sqrt{ (x−1)^2 +(y−2)^2} ,\]
y minimizar la distancia equivale a minimizar el cuadrado de la distancia. Así el problema puede afirmarse como:
\[\nonumber \begin{align}\text{Maximize (and minimize) : }&f (x, y) = (x−1)^2 +(y−2)^2 \\[4pt] \nonumber \text{given : }&g(x, y) = x^2 + y^2 = 80 \end{align} \]
Resolver\(\nabla f (x, y) = \lambda \nabla g(x, y)\) significa resolver las siguientes ecuaciones:
\[\nonumber \begin{align}2(x−1) &= 2\lambda x , \\[4pt] \nonumber 2(y−2) &= 2\lambda y \end{align} \]
Tenga en cuenta que\(x \neq 0\) ya que de lo contrario obtendríamos −2 = 0 en la primera ecuación. De igual manera,\(y \neq 0\). Así podemos resolver ambas ecuaciones para\(\lambda\) lo siguiente:
\[\nonumber \dfrac{x−1}{x} = \lambda = \dfrac{y−2}{y} \Rightarrow x y− y = x y−2x \quad \Rightarrow \quad y = 2x\]
Sustituyendo esto en\(g(x, y) = x^2 + y^2 = 80\) rendimientos\(5x^2 = 80\), entonces\(x = \pm 4\). Entonces los dos puntos críticos restringidos son\((4,8)\text{ and }(−4,−8)\). Ya que\(f (4,8) = 45 \text{ and }f (−4,−8) = 125\), y dado que debe haber puntos en el círculo más cercano y más alejado\((1,2)\), entonces debe darse el caso de que\((4,8)\) sea el punto del círculo más cercano al que\((1,2)\text{ and }(−4,−8)\) esté el más alejado\((1,2)\) (ver Figura 2.7.1).
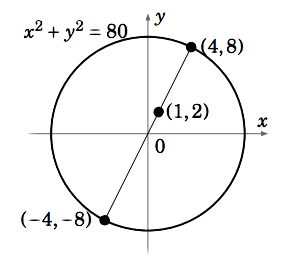
Observe que dado que la ecuación de restricción\(x^2+y^2 = 80\) describe un círculo, que es un conjunto acotado en\(\mathbb{R}^2\), entonces se nos garantizó que los puntos críticos restringidos que encontramos eran de hecho el máximo y el mínimo restringidos.
El método multiplicador Lagrange se puede extender a funciones de tres variables.
Ejemplo 2.27
\[\nonumber \begin{align} \text{Maximize (and minimize) : }&f (x, y, z) = x+ z \\[4pt] \nonumber \text{given : }&g(x, y, z) = x^2 + y^2 + z^2 = 1 \end{align}\]
Solución
Resuelve la ecuación\(\nabla f (x, y, z) = \lambda \nabla g(x, y, z)\):
\[\nonumber \begin{align} 1 &= 2\lambda x \\[4pt] 0 &= 2\lambda y \\[4pt] \nonumber 1 &= 2\lambda z \end{align}\]
La primera ecuación implica\(\lambda \neq 0\) (de lo contrario tendríamos 1 = 0), así podemos dividir por\(\lambda\) en la segunda ecuación para obtener\(y = 0\) y podemos dividir por\(\lambda\) en la primera y tercera ecuaciones para obtener\(x = \dfrac{1}{2\lambda} = z\). Al sustituir estas expresiones en la ecuación de restricción se\(g(x, y, z) = x^2 + y^2 + z^2 = 1\) obtienen los puntos críticos restringidos\(\left (\dfrac{1}{\sqrt{2}},0,\dfrac{1}{\sqrt{2}} \right )\) y\(\left ( \dfrac{−1}{\sqrt{2}} ,0,\dfrac{ −1}{\sqrt{2}}\right )\). Desde\(f \left ( \dfrac{1}{\sqrt{2}} ,0,\dfrac{ 1}{\sqrt{2}}\right ) > f \left ( \dfrac{−1}{\sqrt{2}} ,0,\dfrac{ −1}{\sqrt{2}}\right )\), y dado que la ecuación de restricción\(x^2 + y^2 + z^2 = 1\) describe una esfera (que está delimitada) en\(\mathbb{R}^ 3\), entonces\(\left ( \dfrac{1}{\sqrt{2}} ,0,\dfrac{ 1}{\sqrt{2}}\right )\) es el punto máximo restringido y\(\left ( \dfrac{−1}{\sqrt{2}} ,0,\dfrac{ −1}{\sqrt{2}}\right )\) es el punto mínimo restringido.
Hasta el momento no hemos atribuido importancia alguna al valor del multiplicador de Lagrange\(\lambda\). \(\lambda\)Solo necesitábamos encontrar los puntos críticos restringidos, pero no hicimos uso de su valor. Resulta que\(\lambda\) da una aproximación del cambio en el valor de la función\(f (x, y)\) que deseamos maximizar o minimizar, cuando la constante c en la ecuación de restricción\(g(x, y) = c\) se cambia en 1.
Por ejemplo, en el Ejemplo 2.25 demostramos que el problema de optimización restringida
\[\nonumber \begin{align}\text{Maximize : }&f (x, y) = x y \\[4pt] \nonumber \text{given : }&g(x, y) = 2x+2y = 20 \end{align}\]
tenía la solución\((x, y) = (5,5)\), y eso\(\lambda = \dfrac{x}{2} = \dfrac{y}{2}\). Por lo tanto,\(\lambda = 2.5\). De manera similar podríamos demostrar que el problema de optimización restringida
\[\nonumber \begin{align} \text{Maximize : }&f (x, y) = x y \\[4pt] \nonumber \text{given : }&g(x, y) = 2x+2y = 21 \end{align}\]
tiene la solución\((x, y) = (5.25,5.25)\). Entonces vemos que el valor de\(f (x, y)\) al máximo restringido aumentó de\(f (5,5) = 25 \text{ to }f (5.25,5.25) = 27.5625\), es decir, aumentó en 2.5625 cuando aumentamos el valor de\(c\) en la ecuación de restricción\(g(x, y) = c \text{ from }c = 20 \text{ to }c = 21\). Observe que\(\lambda = 2.5\) está cerca de 2.5625, es decir,
\[\nonumber \lambda \approx \nabla f=f (\text{new max. pt})− f (\text{old max. pt})\]
Por último, señalar que resolver la ecuación\(\nabla f (x, y) = \lambda \nabla g(x, y)\) significa tener que resolver un sistema de dos ecuaciones (posiblemente no lineales) en tres incógnitas, lo que como hemos visto antes, puede que no sea posible hacer. Y el caso de 3 variables puede complicarse aún más. Todo esto restringe de alguna manera la utilidad del método de Lagrange a funciones relativamente simples. Afortunadamente hay muchos métodos numéricos para resolver problemas de optimización restringidos, aunque no los discutiremos aquí.


