3.1: Integrales dobles
- Page ID
- 111233
En el cálculo de una sola variable, la diferenciación y la integración se consideran operaciones inversas. Por ejemplo, para integrar una función es\(f (x)\) necesario encontrar la antiderivada de\(f\), es decir, otra función\(F(x)\) cuya derivada es\(f (x)\). ¿Existe una manera similar de definir la integración de funciones de valor real de dos o más variables? La respuesta es sí, como veremos en breve. Recordemos también que la integral definida de una función no negativa\(f (x) \ge 0\) representaba el área “debajo” de la curva\(y = f (x)\). Como veremos ahora, la doble integral de una función de valor real no negativo\(f (x, y) \ge 0\) representa el volumen “debajo” de la superficie\(z = f (x, y)\).
Dejar\(f (x, y)\) ser una función continua tal que\(f (x, y) \ge 0 \text{ for all }(x, y)\) sobre el rectángulo\(R = {(x, y) : a ≤ x ≤ b, c ≤ y ≤ d}\) en\(\mathbb{R}^2\). A menudo escribiremos esto como\(R = [a,b] \times [c,d]\). Para cualquier número\(x∗\) en el intervalo\([a,b]\), corte la superficie\(z = f (x, y)\) con el plano\(x = x∗\) paralelo al\(yz\) plano. Entonces la traza de la superficie en ese plano es la curva\(f (x∗, y)\), donde\(x∗\) es fija y solo\(y\) varía. El área\(A\) bajo esa curva (es decir, el área de la región entre la curva y el\(x y\) plano) como\(y\) varía a lo largo del intervalo\([c,d]\) entonces depende solo del valor de\(x∗\). Entonces usando la variable\(x\) en lugar de\(x∗\), deja\(A(x)\) ser esa área (ver Figura 3.1.1).
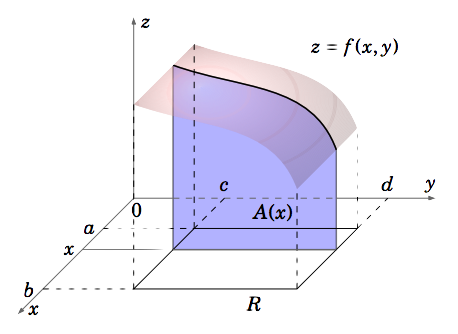
Entonces\(A(x) = \int_c^d f (x, y)d y\) ya que estamos tratando\(x\) como fijos, y solo\(y\) varía. Esto tiene sentido ya que para un fijo\(x\) la función\(f (x, y)\) es una función continua de\(y\) sobre el intervalo\([c,d]\), por lo que sabemos que el área bajo la curva es la integral definida. El área\(A(x)\) es una función de\(x\), así que por el método “slice” o sección transversal del cálculo de una sola variable sabemos que el volumen\(V\) del sólido debajo de la superficie\(z = f (x, y)\) pero por encima del\(x y\) plano -sobre el rectángulo\(R\) es la integral sobre \([a,b]\)de esa área de sección transversal\(A(x)\):
\[V = \int_a^b A(x)dx = \int_a^b \left [\int_c^d f (x, y)d y \right ] dx \label{Eq3.1}\]
Siempre nos referiremos a este volumen como “el volumen debajo de la superficie”. La expresión anterior usa lo que se llama integrales iteradas. Primero la función\(f (x, y)\) se integra como una función de\(y\), tratando la variable\(x\) como una constante (esto se llama integración con respecto a\( y\)). Eso es lo que ocurre en la integral “interna” entre los corchetes en la Ecuación\ ref {Eq3.1}. Esta es la primera integral iterada. Una vez que se realiza esa integración, el resultado es entonces una expresión que involucra únicamente\(x\), que luego se puede integrar con respecto a\(x\). Eso es lo que ocurre en la integral “externa” anterior (la segunda integral iterada). El resultado final es entonces un número (el volumen). Este proceso de pasar por dos iteraciones de integrales se llama doble integración, y la última expresión en la ecuación\ ref {Eq3.1} se llama doble integral.
Observe que integrar\(f (x, y)\) con respecto a\(y\) es la operación inversa de tomar la derivada parcial de\(f (x, y)\) con respecto a\(y\). Además, podríamos haber tomado fácilmente el área de secciones transversales debajo de la superficie que eran paralelas al\(xz\) plano, que entonces dependería solo de la variable\(y\), de manera que el volumen\(V\) sería
\[V = \int_c^d \left [\int_a^b f (x, y)dx \right ] dy \label{Eq3.2}\]
Resulta que en general el orden de las integrales iteradas no importa. Además, usualmente descartaremos los corchetes y simplemente escribiremos
\[V=\int_c^d \int_a^b f (x, y)dx d y \label{Eq3.3}\]
donde se entiende que el hecho de que\(dx\) se escribe antes\(d y\) significa que la función\(f (x, y)\) se integra primero con respecto al\(x\) uso de los límites “internos” de integración\(a \text{ and }b\), y luego la función resultante se integra con respecto a y usando los límites “externos” de integración\(c \text{ and }d\). Este orden de integración se puede cambiar si es más conveniente.
Ejemplo 3.1
Encuentra el volumen\(V\) debajo del plano\(z = 8x +6y\) sobre el rectángulo\(R = [0,1]\times [0,2]\).
Solución
Eso lo vemos\(f (x, y) = 8x+6y \ge 0 \text{ for }0 \le x \le 1 \text{ and }0 \le y \le 2\), entonces:
\[\nonumber \begin{align} V&=\int_0^2 \int_0^1 (8x+6y)dx \,d y \\[4pt] \nonumber &= \int_0^2 \left ( 4x^2 +6x y \big |_{x=0}^{x=1} \right )dy \\[4pt] \nonumber &=\int_0^2 (4+6y)d y \\[4pt] \nonumber &=4y+3y^2 \big |_0^2 \\[4pt] &=20 \end{align}\]
Supongamos que habíamos cambiado el orden de integración. Podemos verificar que seguimos obteniendo la misma respuesta:
\[\nonumber \begin{align}V&=\int_0^1 \int_0^2 (8x+6y)dy \,d x \\[4pt] \nonumber &=\int_0^1 \left ( 8x y+3y^2 \big |_{y=0}^{y=2} \right )dx \\[4pt] \nonumber &=\int_0^1 (16x+12)dx \\[4pt] &=8x^2 +12x \big |_0^1 \\[4pt] \nonumber &=20 \end{align}\]
Ejemplo 3.2
Encuentra el volumen\(V\) debajo de la superficie\(z = e^{x+y}\) sobre el rectángulo\(R = [2,3] \times [1,2]\).
Solución
Eso lo sabemos\(f (x, y) = e^{x+y} > 0 \text{ for all }(x, y)\), entonces
\[\nonumber \begin{align} V &=\int_1^2 \int_2^3 e^{x+y} dx\, d y \\[4pt] \nonumber &= \int_1^2 \left (e^{x+y} \big |_{x=2}^{x=3} \right )dy \\[4pt] \nonumber &= \int_1^2 (e^{y+3}-e^{y+2})dy \\[4pt] \nonumber &= e^{y+3}-e^{y+2} \big |_1^2 \\[4pt] \nonumber &= e^5 − e^4 −(e^4 − e^3 ) = e^5 −2e^4 + e^3 \end{align} \]
Recordemos que para una función general\(f (x)\), la integral\(\int_a^b f (x)dx\) representa la diferencia del área por debajo de la curva\(y = f (x)\) pero por encima del\(x\) eje cuando\(f (x) \ge 0\), y el área por encima de la curva pero por debajo del\(x\) -eje cuando\(f (x) \le 0\). De igual manera, la doble integral de cualquier función continua\(f (x, y)\) representa la diferencia del volumen por debajo de la superficie\(z = f (x, y)\) pero por encima del\(x y\) plano cuando\(f (x, y) \ge 0\), y el volumen por encima de la superficie pero por debajo del\(x y\) plano cuando\(f (x, y) \le 0\). Así, nuestro método de doble integración por medio de integrales iteradas puede ser utilizado para evaluar la doble integral de cualquier función continua sobre un rectángulo, independientemente de si\(f (x, y) \ge 0\) o no.
Ejemplo 3.3
Evaluar\(\int_0^{2\pi}\int_0^{\pi}sin(x+y)dx\,dy \)
Solución
Tenga en cuenta que\(f (x, y) = sin(x+ y)\) es tanto positivo como negativo sobre el rectángulo\([0,\pi]\times [0,2\pi]\). Todavía podemos evaluar la doble integral:
\[\nonumber \begin{align} \int_0^{2\pi} \int_0^{\pi}sin(x+y)dx\,dy &=\int_0^{2\pi} \left (-cos(x+y)\big |_{x=0}^{x=\pi} \right )dy \\[4pt] \nonumber &= \int_0^{2\pi} (-cos(y+\pi)+cos{\,y})dy \\[4pt] \nonumber &=-sin(y+\pi)+sin{\,y}\big |_0^{2\pi} = -sin{\,3\pi}+sin{\,2\pi} - (-sin{\,\pi}+sin{\,0}) \\[4pt] \nonumber &=0 \end{align} \]


