3.2: Integrales dobles sobre una región general
- Page ID
- 111260
En la sección anterior nos dimos una idea de lo que representa una doble integral sobre un rectángulo. Ahora podemos definir la doble integral de una función de valor real\(f (x, y)\) sobre regiones más generales en\(\mathbb{R}^2\).
Supongamos que tenemos una región\(R\) en el\(x y\) plano -que está delimitada a la izquierda por la línea vertical\(x = a\), delimitada a la derecha por la línea vertical\(x = b\) (donde\(a < b\)), delimitada por debajo por una curva\(y = g_1(x)\), y delimitada arriba por una curva\(y = g_2(x)\), como en la Figura 3.2.1 (a). Supondremos que\(g_1(x) \text{ and }g_2(x)\) no se cruzan en el intervalo abierto\((a,b)\) (aunque podrían cruzarse en los puntos finales\(x = a \text{ and }x = b\)).
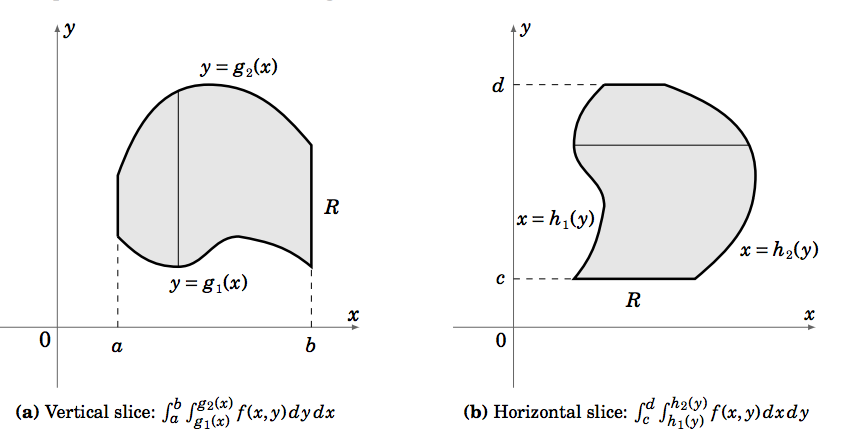
Luego, usando el método slice de la sección anterior, la doble integral de una función de valor real\(f (x, y)\) sobre la región\(R\), denotada por\(\iint\limits_R f (x, y)d A\), viene dada por
\[\iint\limits_R f (x, y)d A = \int_a^b \left [ \int_{g_1(x)}^{g_2(x)}f (x, y)d y \right ]dx \label{Eq3.4} \]
Esto significa que tomamos cortes verticales en la región\(R\) entre las curvas\(y = g_1(x) \text{ and }y = g_2(x)\). El símbolo a veces\(d A\) se denomina elemento de área o infinitesimal, con el área\(A\) significante. Nótese que primero\(f (x, y)\) se integra con respecto a\(y\), con funciones de\(x\) como los límites de la integración. Esto tiene sentido ya que el resultado de la primera integral iterada tendrá que ser una función de\(x\) solo, lo que luego nos permite tomar la segunda integral iterada con respecto a\(x\).
Del mismo modo, si tenemos una región\(R\) en el\(x y\) plano -que está delimitada a la izquierda por una curva\(x = h_1(y)\), delimitada a la derecha por una curva\(x = h_2(y)\), delimitada por debajo por la línea horizontal\(y = c\), y delimitada arriba por la línea horizontal\(y = d\) (donde\(c < d\)), como en la Figura 3.2.1 (b) ( asumiendo que\(h_1(y)\text{ and }h_2(y)\) no se cruzan en el intervalo abierto\((c,d)\)), luego tomar cortes horizontales da
\[\iint\limits_R f (x, y)d A = \int_c^d \left [ \int_{h_1(y)}^{h_2(y)}f (x, y)dx \right ]dy \label{Eq3.5}\]
Observe que estas definiciones incluyen el caso cuando la región\(R\) es un rectángulo. También, si\(f (x, y) \ge 0\) para todos\((x, y)\) en la región\(R\), entonces\(\iint\limits_R f (x, y)d A\) es el volumen debajo de la superficie\(z = f (x, y) \text{ over the region }R\).
Ejemplo 3.4
Encuentra el volumen\(V\) debajo del avión\(z = 8x+6y\) sobre la región\(R = {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 2x^2 }\).
La región\(R\) se muestra en la Figura 3.2.2. Usando rebanadas verticales obtenemos:
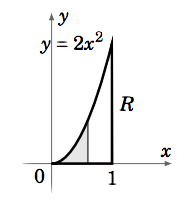
\[\nonumber \begin{align} V &=\iint\limits_R (8x+6y)d A \\[4pt] \nonumber &= \int_0^1 \left [ \int_0^{2x^2} (8x+6y)d y \right ]dx \\[4pt] \nonumber &= \int_0^1 \left (8x y+3y^2 \big |_{y=0}^{y=2x^2} \right )dx \\[4pt] \nonumber &= \int_0^1 (16x^3 +12x^4 )dx \\[4pt] \nonumber &= 4x^4 + \dfrac{12}{5} x^5 \Big |_0^1 = 4 + \dfrac{12}{5} = \dfrac{32}{5} = 6.4 \end{align}\]
Obtenemos la misma respuesta usando rebanadas horizontales (ver Figura 3.2.3):
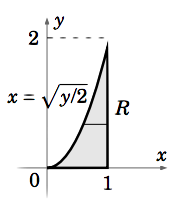
\[\nonumber \begin{align} V &=\iint\limits_R (8x+6y)d A \\[4pt] \nonumber &=\int_0^2 \left [ \int_{\sqrt{y/2}}^{1}(8x+6y)dx \right ] dy \\[4pt] \nonumber &=\int_0^2 \left (4x^2 +6x y \big |_{x=\sqrt{y/2}}^{x=1} \right )dy \\[4pt] \nonumber &= \int_0^2 (4+6y - (2y + \dfrac{6}{\sqrt{2}}y\sqrt{y}))dy = \int_0^2 (4+4y-3\sqrt{2} y^{3/2})dy \\[4pt] \nonumber &= 4y +2y^2 -\dfrac{6\sqrt{2}}{5}y^{5/2} \big |_0^2 = 8+8-\dfrac{6\sqrt{2}\sqrt{32}}{5} = 16-\dfrac{48}{5}=\dfrac{32}{5}=6.4 \end{align}\]
Ejemplo 3.5
Encuentra el volumen\(V\) del sólido delimitado por los tres planos de coordenadas y el plano\(2x+ y+4z = 4\).
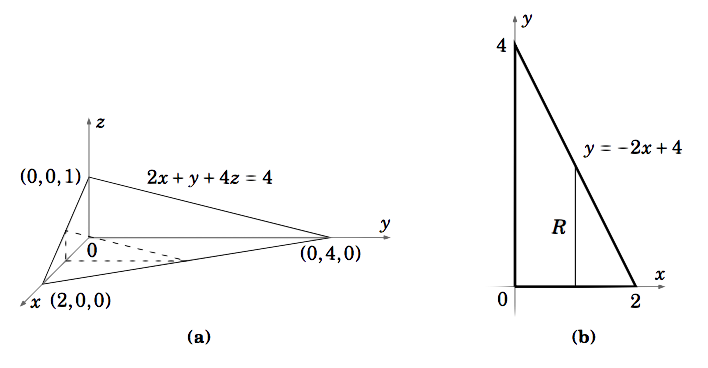
Solución
El sólido se muestra en la Figura 3.2.4 (a) con un corte vertical típico. El volumen\(V\) viene dado por\(\iint\limits_R f (x, y)d A\), dónde\(f (x, y) = z = \dfrac{1}{4} (4−2x − y)\) y la región\(R\), que se muestra en la Figura 3.2.4 (b), es\(R = {(x, y) : 0 ≤ x ≤ 2, 0 ≤ y ≤ −2x+4}\). Uso de rebanadas verticales en\(R\) da
\[\nonumber \begin{align} V &= \iint\limits_R \dfrac{1}{4} (4−2x− y)d A \\[4pt] \nonumber &= \int_0^2 \left [ \int_0^{-2x+4}\dfrac{1}{4} (4−2x− y)d y \right ]dx \\[4pt] \nonumber &= \int_0^2 \left ( − \dfrac{1}{8} (4−2x− y)^2 \big |_{y=0}^{y=-2x+4} \right )dx \\[4pt] \nonumber &= \int_0^2 \dfrac{1}{8}(4-2x)^2 dx \\[4pt] \nonumber &= -\dfrac{1}{48}(4-2x)^3 \big |_0^2 = \dfrac{64}{48} =\dfrac{4}{3} \end{align} \]
Para una región general\(R\), que puede no ser uno de los tipos de regiones que hemos considerado hasta ahora, la doble integral\(\iint\limits_R f (x, y)d A\) se define de la siguiente manera. Supongamos que\(f (x, y)\) es una función de valor real no negativo y que\(R\) es una región delimitada en\(\mathbb{R}^2\), por lo que se puede encerrar en algún rectángulo\([a,b]\times [c,d]\). Luego divide ese rectángulo en una cuadrícula de subrectángulos. Solo considere los subrectángulos que están encerrados completamente dentro de la región\(R\), como lo muestran los subrectángulos sombreados en la Figura 3.2.5 (a). En cualquiera de esos subrectángulos\([x_i , x_{i+1}] \times [y_j , y_{j+1}]\), elija un punto\((x_{i∗}, y_{j∗})\). Entonces el volumen bajo la superficie\(z = f (x, y)\) sobre ese subrectángulo es aproximadamente\(f (x_{i∗}, y_{j∗})\Delta x_i \Delta y_j\), donde\(\Delta x_i = x_{i+1} − x_i , \Delta y_j = y_{j+1} − y_j ,\text{ and }f (x_{i∗}, y_{j∗})\) está la altura y\(\Delta x_i \Delta y_j\) es el área base de un paralelepípedo, como se muestra en la Figura 3.2.5 (b). Entonces el volumen total debajo de la superficie es aproximadamente la suma de los volúmenes de todos esos paralelepípedos, a saber
\[\sum\limits_j \sum\limits_i f (x_{i∗}, y_{j∗})\Delta x_i \Delta y_j \label{Eq3.6}\]
donde la suma ocurre sobre los índices de los subrectángulos interiores\(R\). Si tomamos subrectángulos cada vez más pequeños, de manera que la longitud de la diagonal más grande de los subrectángulos vaya a 0, entonces los subrectángulos comienzan a llenar cada vez más de la región\(R\), y así la suma anterior se acerca al volumen real debajo de la superficie\(z = f (x, y)\) sobre la región\(R\). Luego definimos\(\iint\limits_R f (x, y)d A\) como el límite de esa doble suma (el límite se toma sobre todas las subdivisiones del rectángulo\([a,b] \times [c,d]\) ya que la diagonal más grande de los subrectángulos va a 0).
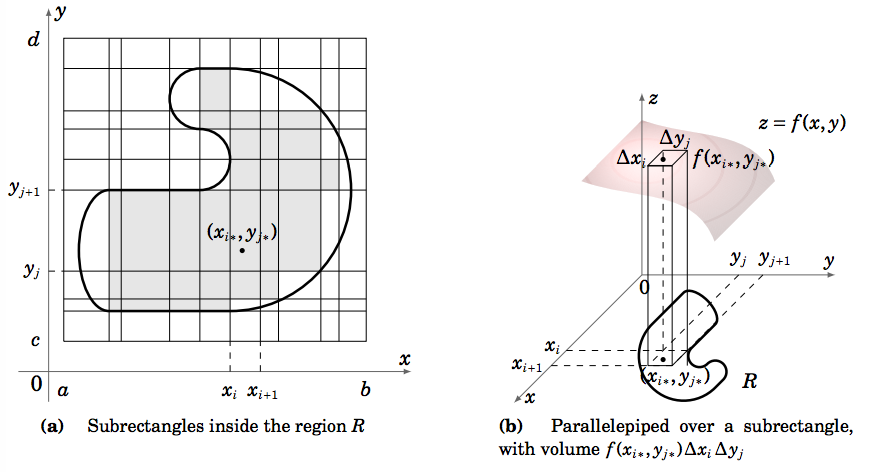
Se puede hacer una definición similar para una función\(f (x, y)\) que no necesariamente siempre es negativa: simplemente reemplace cada mención de volumen por el volumen negativo en la descripción anterior cuando\(f (x, y) < 0\). En el caso de una región del tipo mostrado en la Figura 3.2.1, utilizando la definición de la integral de Riemann a partir del cálculo de una sola variable, nuestra definición de\(\iint\limits_R f (x, y)d A\) reduce a una secuencia de dos integrales iteradas.
Por último, la región\(R\) no tiene que ser acotada. Podemos evaluar integrales dobles impropias (es decir, sobre una región no delimitada, o sobre una región que contiene puntos donde la función no\(f (x, y)\) está definida) como una secuencia de integrales de variable única impropias iteradas.
Ejemplo 3.6
Evaluar\(\int_1^{\infty}\int_0^{1/x^2} 2y d y\, dx\)
Solución
\[\nonumber \begin{align} \int_1^{\infty}\int_0^{1/x^2} 2ydy\,dx &= \int_1^{\infty} \left ( y^2 \Big |_{y=0}^{y=1/x^2} \right )dx \\[4pt] \nonumber &= \int_1^{\infty}x^{-4}dx= -\dfrac{1}{3}x^{-3} \Big |_1^{\infty} = 0-(-\dfrac{1}{3}) = \dfrac{1}{3} \end{align} \]


