3.6: Aplicación- Centro de Masa
- Page ID
- 111247
Recordemos del cálculo de una sola variable que para una región\(R = {(x, y) : a ≤ x ≤ b,0 ≤ y ≤ f (x)}\) en la\(\mathbb{R}^2\) que representa una placa delgada y plana (Figura 3.6.1), donde\(f (x)\) es una función continua en\([a,b]\), el centro de masa de\(R\) tiene coordenadas\((\bar x, \bar y)\) dadas por
\[ \bar x =\dfrac{M_y}{M} \text{ and }\bar y = \dfrac{M_x}{M}\]
donde
\[M_x = \int_a^b \dfrac{(f(x))^2}{2}dx,\quad M_y = \int_a^b x f (x)\,dx, \quad M=\int_a^b f (x)\,dx \label{Eq3.27}\]
asumiendo que\(R\) tiene una densidad uniforme, es decir, la masa de\(R\) se distribuye uniformemente sobre la región. En este caso el área\(M\) de la región se considera la masa de\(R\) (la densidad es constante, y se toma como 1 por simplicidad).
En el caso general donde la densidad de una región (o lámina)\(R\) es una función continua\(δ = δ(x, y)\) de las coordenadas\((x, y)\) de puntos dentro\(R\) (donde\(R\) puede estar cualquier región en\(\mathbb{R}^2\)) se\(R\) dan las coordenadas\((\bar x,\bar y)\) del centro de masa de por
\[\bar x =\dfrac{M_y}{M} \text{ and }\bar y = \dfrac{M_x}{M}\label{Eq3.28}\]
donde
\[M_y = \iint\limits_R xδ(x, y)\,d A ,\quad M_x = \iint\limits_R yδ(x, y)\,d A,\quad M=\iint\limits_R δ(x, y)\,d A ,\label{Eq3.29}\]
\(M_x \text{ and }M_y\)Las cantidades se denominan los momentos (o primeros momentos) de la región\(R\) alrededor del\(x\) eje -eje y\(y\) -eje, respectivamente. La cantidad\(M\) es la masa de la región\(R\). Para ver esto, piensa en llevar un pequeño rectángulo en su interior\(R\) con dimensiones\(∆x \text{ and }∆y\) cercanas a 0. La masa de ese rectángulo es aproximadamente\(δ(x_∗, y_∗)∆x∆y\), por algún punto\((x_∗, y_∗)\) en ese rectángulo. Entonces la masa de\(R\) es el límite de las sumas de las masas de todos esos rectángulos dentro\(R\) como las diagonales de los rectángulos se acercan a 0, que es la doble integral\(\iint\limits_R δ(x, y)\,d A\).
Tenga en cuenta que las fórmulas en la Ecuación\ ref {Eq3.27} representan un caso especial cuando a\(δ(x, y) = 1\) lo largo\(R\) de las fórmulas en la Ecuación\ ref {Eq3.29}.
Ejemplo 3.13: Centro de masa de una región 2D
Encuentra el centro de masa de la región\(R = {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 2x^2 }\), si la densidad funciona en\((x, y) \text{ is }δ(x, y) = x+ y\).
Solución:
La región\(R\) se muestra en la Figura 3.6.2. Tenemos
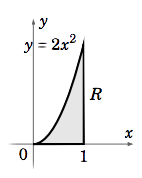
\[\nonumber \begin{align} M&=\iint\limits_R δ(x, y)\,d A \\[4pt] \nonumber &= \int_0^1 \int_0^{2x^2}(x+ y)\,d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( xy + \dfrac{y^2}{2} \Big |_{y=0}^{y=2x^2} \right ) \,dx \\[4pt] \nonumber &=\int_0^1 (2x^3 +2x^4 )\,dx \\[4pt] \nonumber &= \dfrac{x^4}{2}+\dfrac{2x^5}{5} \Big |_0^1 = \dfrac{9}{10}\\[4pt] \end{align}\]
y
\[\nonumber \begin{split} M_x &= \iint\limits_R yδ(x, y)\,d A \\[4pt] \nonumber &=\int_0^1 \int_0^{2x^2} y(x+ y)\,d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( \dfrac{xy^2}{2}+\dfrac{y^3}{3} \Big |_{y=0}^{y=2x^2} \right )\,dx \\[4pt] \nonumber &=\int_0^1 (2x^5 + \dfrac{8x^6}{ 3} )\,dx \\[4pt] \nonumber &=\dfrac{x^6}{3} + \dfrac{8x^7}{21} \Big |_0^1 = \dfrac{5}{7} \\[4pt] \end{split} \qquad \nonumber \begin{split} M_y &= \iint\limits_R xδ(x, y)\,d A \\[4pt] \nonumber &=\int_0^1 \int_0^{2x^2} x(x+ y)\,d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( x^2y+\dfrac{xy^2}{2} \Big |_{y=0}^{y=2x^2} \right )\,dx \\[4pt] \nonumber &=\int_0^1 (2x^4 + 2x^5 )\,dx \\[4pt] &=\dfrac{2x^5}{5} + \dfrac{x^6}{3} \Big |_0^1 = \dfrac{11}{15} \\[4pt] \end{split}\]
por lo que el centro de masa\((\bar x,\bar y)\) está dado por
\[\nonumber \bar x =\dfrac{M_y}{M} = \dfrac{11/15}{9/10} = \dfrac{22}{27},\quad \bar y = \dfrac{M_x}{M} = \dfrac{5/7}{9/10}=\dfrac{50}{63}\]
Observe cómo este centro de masa está un poco más hacia la esquina superior de la región\(R\) que cuando la densidad es uniforme (es fácil usar las fórmulas en la Ecuación\ ref {Eq3.27} para mostrar eso\((\bar x,\bar y) = \left ( \dfrac{3}{ 4} , \dfrac{3}{ 5} \right ) \) en ese caso). Esto tiene sentido ya que la función de densidad\(δ(x, y) = x + y\) aumenta a medida que se\((x, y)\) acerca a esa esquina superior, donde hay bastante área.
En el caso especial donde la función de densidad\(δ(x, y)\) es una función constante en la región\(R\), el centro de masa\((\bar x,\bar y)\) se denomina centroide de\(R\).
Las fórmulas para el centro de masa de una región en\(\mathbb{R}^2\) pueden generalizarse a un sólido\(S\) en\(\mathbb{R}^ 3\). Dejar\(S\) ser un sólido con una función de densidad de masa continua\(δ(x, y, z)\) en cualquier punto\((x, y, z)\) de\(S\). Entonces el centro de masa de\(S\) tiene coordenadas\((\bar x,\bar y,\bar z)\), donde
\[\bar x = \dfrac{M_{yz}}{M},\quad \bar y = \dfrac{M_{xz}}{M},\quad \bar z= \dfrac{M_{xy}}{M},\label{Eq3.30}\]
donde
\[M_{yz} = \iiint\limits_S xδ(x, y, z)\,dV, \quad M_{xz} = \iiint\limits_S yδ(x, y, z)\,dV,\quad M_{xy} = \iiint\limits_S zδ(x, y, z)\,dV ,\label{Eq3.31}\]
\[M = \iiint\limits_S δ(x, y, z)\,dV .\label{Eq3.32}\]
En este caso,\(M_{yz}, M_{xz}\text{ and }M_{x y}\) se denominan los momentos (o primeros momentos) de\(S\) alrededor del\(yz\) -plano,\(xz\) -plano y\(x y\) -plano, respectivamente. También,\(M\) es la masa de\(S\).
Ejemplo 3.14: Centro de masa de un sólido 3D
Encuentre el centro de masa del sólido\(S = {(x, y, z) : z ≥ 0, x^2 + y^2 + z^2 ≤ a^2 }\), si la densidad funciona en\((x, y, z) \text{ is }δ(x, y, z) = 1\).
Solución:
El sólido\(S\) es solo el hemisferio superior dentro de la esfera de radio\(a\) centrada en el origen (ver Figura 3.6.3).
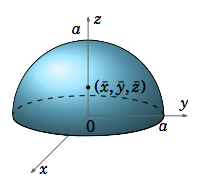
Entonces dado que la función de densidad es una constante y\(S\) es simétrica alrededor del\(z\) -eje, entonces es claro que\(\bar x = 0 \text{ and }\bar y = 0\), así que sólo necesitamos encontrar\(\bar z\). Tenemos
\[\nonumber M = \iiint\limits_S δ(x, y, z)\,dV = \iiint\limits_S 1dV = \text{ Volume}(S).\]
Pero como el volumen de\(S\) es la mitad del volumen de la esfera de radio\(a\), lo que sabemos por el Ejemplo 3.12 es\(\dfrac{4\pi a}{3}\), entonces\(M = \dfrac{2\pi a}{3}\). Y
\[\nonumber \begin{align} M_{xy} &= \iiint\limits_S zδ(x, y, z)\,dV \\[4pt] \nonumber &=\iiint\limits_S z \,dV,\text{ which in spherical coordinates is} \\[4pt] \nonumber &=\int_0^{2\pi} \int_0^{\pi /2} \int_0^a (ρ \cos{φ})ρ^2 \sin{φ}\,dρ\, dφ\,dθ \\[4pt] \nonumber &=\int_0^{2\pi} \int_0^{\pi/2} \sin{φ} \cos{φ} \left ( \int_0^a ρ^3 \,dρ \right ) \,dφ\,dθ \\[4pt] \nonumber &= \int_0^{2\pi} \int_0^{\pi/2} \dfrac{a^4}{4} \sin{φ} \cos{φ}\,dφ\,dθ \\[4pt] \nonumber M_{xy}&=\int_0^{2\pi} \int_0^{\pi/2} \dfrac{a^4}{8} \sin{2φ}\,dφ\,dθ \quad (\text{since }\sin{2φ} = 2\sin{φ} \cos{φ}) \\[4pt] \nonumber &= \int_0^{2\pi} \left ( -\dfrac{a^4}{16} \cos{2φ} \Big |_{φ=0}^{ φ=\pi/2}\right ) \,dθ \\[4pt] \nonumber &=\int_0^{2\pi} \dfrac{a^4}{8}\,dθ \\[4pt] &=\dfrac{\pi a^4}{4}, \\[4pt] \end{align}\]
entonces
\[\nonumber \bar z = \dfrac{M_{xy}}{M} = \dfrac{\dfrac{\pi a^4}{4}}{\dfrac{2\pi a^3}{3}}=\dfrac{3a}{8}.\]
Así, el centro de masa de\(S\) es\((\bar x,\bar y,\bar z) = \left ( 0,0, \dfrac{3a}{8} \right ).\)


