1.6: Los Derivados

Ahora volvemos al problema de las tasas de cambio. Dado\(y=f(x),\) por cualquier infinitesimal\(d x\) dejamos

\[d y=f(x+d x)-f(x) .\] Si\(y\) es una función continua de\(x,\) entonces\(d y\) es infinitesimal y, si\(d x \neq 0,\) la relación \[\frac{d y}{d x}=\frac{f(x+d x)-f(x)}{d x}\] es un número hiperreal. Si\(\frac{d y}{d x}\) es finito, entonces su sombra, si es lo mismo para todos los valores de\(d x,\) es la tasa de cambio de\(y\) con respecto a la\(x,\) cual llamaremos la derivada de\(y\) con respecto a\(x .\)

Definición

Dado\(y=f(x),\) supongamos

\[\frac{d y}{d x}=\frac{f(x+d x)-f(x)}{d x}\] es finito y tiene la misma sombra para todos los infinitesimales distintos de cero\(d x .\) Entonces llamamos a \[\operatorname{sh}\left(\frac{d y}{d x}\right)\] la derivada de\(y\) con respecto a\(x .\)

Obsérvese que el cociente en\((1.6 .3)\) será infinito si no\(f(x+d x)-f(x)\) es un infinitesimal. Por lo tanto, una función que no es continua en\(x\) no puede tener una derivada en\(x .\)

Existen numerosas formas de denotar la derivada de una función\(y=f(x) .\) Uno es usar\(\frac{d y}{d x}\) para denotar, dependiendo del contexto, tanto la relación de los infinitesimales como\(d y\)\(d x\) y la sombra de esta relación, que es la derivada. Otra es escribir\(f^{\prime}(x)\) para la derivada de la función\(f .\) Vamos a utilizar ambas notaciones extensivamente.

Ejemplo\(\PageIndex{1}\)

Si\(y=x^{2},\) entonces, para cualquier infinitesimal distinto de cero\(d x\),

\[d y=(x+d x)^{2}-x^{2}=\left(x^{2}+2 x d x+(d x)^{2}\right)-x^{2}=(2 x+d x) d x .\] De ahí \[\frac{d y}{d x}=2 x+d x \simeq 2 x\] y así la derivada de\(y\) con respecto a\(x\) es \[\frac{d y}{d x}=2 x.\]

Ejemplo\(\PageIndex{2}\)

Si\(f(x)=4 x,\) entonces, para cualquier infinitesimal distinto de cero\(d x\),

\[\frac{f(x+d x)-f(x)}{d x}=\frac{4(x+d x)-4 x}{d x}=\frac{4 d x}{d x}=4 .\] Por lo tanto,\(f^{\prime}(x)=4 .\) tenga en cuenta que esto implica que\(f(x)\) tiene una tasa de cambio constante: cada cambio de una unidad en\(x\) resulta en un cambio de 4 unidades en\(f(x) .\)

Ejercicio\(\PageIndex{1}\)

Encuentra\(\frac{d y}{d x}\) si\(y=5 x-2\).

Contestar

\(\frac{d y}{d x}=5\)

Ejercicio\(\PageIndex{2}\)

Encuentra\(\frac{d y}{d x}\) si\(y=x^{3}\).

Contestar

\(\frac{d y}{d x}=3 x^{2}\)

Ejercicio\(\PageIndex{3}\)

Encuentra\(f^{\prime}(x)\) si\(f(x)=4 x^{2}\).

Para denotar la tasa de cambio de\(y\) con respecto\(x\) a a un valor particular de\(x,\) decir, cuando\(x=a,\) escribimos \[\left.\frac{d y}{d x}\right|_{x=a}.\] Si\(y=f(x),\) entonces, por supuesto, esto es lo mismo que escribir\(f^{\prime}(a)\).

Contestar

\(f^{\prime}(x)=8 x\)

Ejemplo\(\PageIndex{3}\)

Si\(y=x^{2},\) entonces vimos por encima de eso\(\frac{d y}{d x}=2 x .\) De ahí la tasa de cambio de\(y\) con respecto a\(x\) cuando\(x=3\) es

\[\left.\frac{d y}{d x}\right|_{x=3}=(2)(3)=6 .\]

Ejemplo\(\PageIndex{4}\)

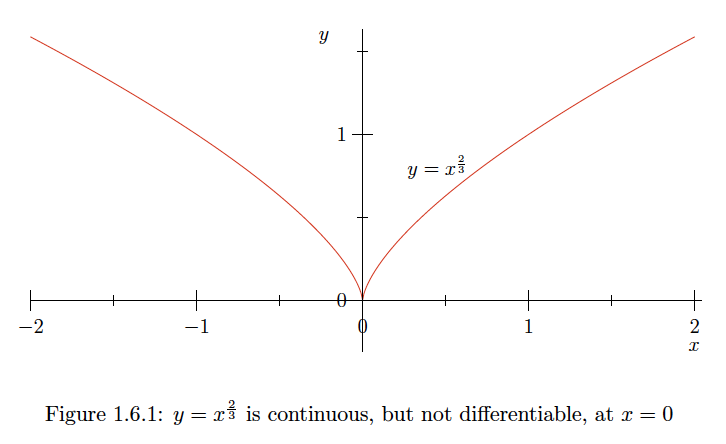
Si\(f(x)=x^{\frac{2}{3}},\) entonces por cualquier infinitesimal\(d x\),

\[f(0+d x)-f(0)=f(d x)=(d x)^{\frac{2}{3}} ,\] que es infinitesimal. De ahí que\(f\) sea continuo en\(x=0 .\) Ahora si\(d x \neq 0,\) entonces \[\frac{f(0+d x)-f(0)}{d x}=\frac{(d x)^{\frac{2}{3}}}{d x}=\frac{1}{(d x)^{\frac{1}{3}}} .\] Dado que esto es infinito,\(f\) no tiene una derivada\(x=0 .\) en En particular, esto demuestra que una función puede ser continua en un punto, pero no diferenciable en ese punto. Ver Figura\(1.6 .1 .\)

Ejemplo\(\PageIndex{5}\)

Si\(f(x)=\sqrt{x},\) entonces, como hemos visto anteriormente, para cualquier\(x>0\) infinitesimal distinto de cero\(d x\),

\[\begin{aligned} f(x+d x)-f(x) &=\sqrt{x+d x}-\sqrt{x} \\[8pt] &=(\sqrt{x+d x}-\sqrt{x}) \frac{\sqrt{x+d x}+\sqrt{x}}{\sqrt{x+d x}+\sqrt{x}} \\[8pt] &=\frac{(x+d x)-x}{\sqrt{x+d x}+\sqrt{x}} \\[8pt] &=\frac{d x}{\sqrt{x+d x}+\sqrt{x}}. \end{aligned}\] Ahora se deduce que \[\frac{f(x+d x)-f(x)}{d x}=\frac{1}{\sqrt{x+d x}+\sqrt{x}} \simeq \frac{1}{\sqrt{x}+\sqrt{x}}=\frac{1}{2 \sqrt{x}} .\] Así \[f^{\prime}(x)=\frac{1}{2 \sqrt{x}} .\] Por ejemplo, la tasa de cambio de\(y\) con respecto a\(x\) cuándo\(x=9\) es A veces también \[f^{\prime}(9)=\frac{1}{2 \sqrt{9}}=\frac{1}{6} .\] escribiremos \[\frac{d}{d x} f(x)\] para\(f^{\prime}(x) .\) Con esta notación, podríamos escribir el resultado de el ejemplo anterior como \[\frac{d}{d x} \sqrt{x}=\frac{1}{2 \sqrt{x}} .\]

Definición

Dada una función\(f,\) si\(f^{\prime}(a)\) existe decimos que\(f\) es diferenciable en\(a .\) Decimos\(f\) es diferenciable en un intervalo abierto\((a, b)\) si\(f\) es diferenciable en cada punto\(x\) en\((a, b) .\)

Ejemplo\(\PageIndex{6}\)

La función\(y=x^{2}\) es diferenciable en\((-\infty, \infty)\).

Ejemplo\(\PageIndex{7}\)

La función\(f(x)=\sqrt{x}\) es diferenciable en\((0, \infty) .\) Note que no\(f\) es diferenciable\(x=0\) ya que no\(f(0+d x)=f(d x)\) está definida para todos los infinitesimales\(d x .\)

Ejemplo\(\PageIndex{8}\)

La función no\(f(x)=x^{\frac{2}{3}}\) es diferenciable en\(x=0\).