2.1: Integrales

Ahora dirigimos nuestra atención al otro lado de la paradoja de la flecha de Zenón. En el capítulo anterior comenzamos con el problema de encontrar la velocidad de un objeto dada una función que definía la posición del objeto en cada instante del tiempo. Ahora suponemos que se nos da una función que especifica la velocidad\(v\) de un objeto, moviéndose a lo largo de una línea recta, en cada instante del tiempo\(t,\) y deseamos encontrar la posición\(x\) del objeto en el momento\(t .\) Hay dos enfoques para encontrar\(x ;\) investigaremos ambos, llevándonos al teorema fundamental del cálculo.

Primero, de nuestro trabajo anterior sabemos que\(v\) es el derivado de\(x .\) Eso es, de\[\frac{d x}{d t}=v .\] ahí que para encontrar\(x\) necesitamos encontrar una función que tenga\(v\) para su derivada.

Definición

Dada una función\(f\) definida en un intervalo abierto\((a, b),\) llamamos a una función\(F\) una integral de\(f\) if\(F^{\prime}(x)=f(x)\) for all\(x\) in\((a, b)\).

Ejemplo\(\PageIndex{1}\)

Si\(f(x)=3 x^{2},\) entonces\(F(x)=x^{3}\) es una integral de\(f\) on\((-\infty, \infty)\) ya\(F^{\prime}(x)=3 x^{2}\) para todos\(x .\) Sin embargo, tenga en cuenta que no\(F\) es la única integral de\(f:\) para otros ejemplos, ambos\(G(x)=x^{3}+4\) y\(H(x)=x^{3}+15\) son integrales de\(f\) también. De hecho, dado que la derivada de una constante es 0 la función\(L(x)=x^{3}+c\) es una integral de\(f\) para cualquier constante\(c .\)

En general, si\(F\) es una integral de\(f,\) entonces también\(G(x)=F(x)+c\) es una integral de\(f\) para cualquier constante ¿\(c\)Hay alguna otra integral de Es\(f ?\) decir, si empezamos con ambos\(F\) y\(G\) siendo integrales de\(f,\) sigue eso\(G(x)-F(x)=c\) para algunos constante\(c\) y para todos\(x ?\) Para responder a esta pregunta, primero tenga en cuenta que si dejamos\(H(x)=G(x)-F(x),\) entonces

\[H^{\prime}(x)=G^{\prime}(x)-F^{\prime}(x)=f(x)-f(x)=0\]para todos\(x .\) De ahí\(H\) es una integral de la función constante\(g(x)=0\) para todos\(x .\) Así que nuestra pregunta se convierte en: Si\(H^{\prime}(x)=0\) para todos\(x,\) sigue eso\(H(x)=c\) para alguna constante\(c\) y todo\(x ?\) Si lo hace, entonces\[c=H(x)=F(x)-G(x) ,\] y de hecho \(F\)y\(G\) difieren solo por una constante. Entonces supongamos que nos dan\(H^{\prime}(x)=0\) para todos\(x\) en un intervalo abierto\((a, b) .\) Entonces, para dos puntos cualesquiera\(u<v\) en\((a, b),\) él se deduce del teorema del valor medio que\[H(v)-H(u)=H^{\prime}(d)(u-v)\] para algunos\(d\) en\((a, b) .\) Pero entonces\(H^{\prime}(d)=0,\) así es\(H(v)-H(u)=0,\) decir,\(H(u)=\)\(H(v) .\) Ya que esto es cierto para cualquier punto arbitrario\(u\) y\(v\) en\((a, b),\) ello se deduce que\(H\) debe ser constante en\((a, b) .\)

Teorema\(\PageIndex{1}\)

Si\(F^{\prime}(x)=G^{\prime}(x)\) para todos\(x\) en\((a, b),\) entonces existe una constante\(c\) tal que\(G(x)=F(x)+c\) para todos\(x\) en\((a, b)\).

En particular, si\(F^{\prime}(x)=0\) para todos\(x\) en\((a, b),\) entonces\(F\) es constante on\((a, b)\).

Ejemplo\(\PageIndex{2}\)

Desde

\[\frac{d}{d x}\left(\frac{3}{2} x^{2}+4 x\right)=3 x+4 ,\]cualquier integral de\(f(x)=3 x+4\) debe ser de la forma\[F(x)=\frac{3}{2} x^{2}+4 x+c\] para alguna constante\(c\).

Denotamos una integral de una función\(f\) por

\[\int f(x) d x .\]

La motivación para esta notación será más evidente una vez que discutamos el teorema fundamental del cálculo.

Ejemplo\(\PageIndex{3}\)

Desde

\[\frac{d}{d x}\left(4 x^{3}-\sin (x)\right)=12 x^{2}-\cos (x),\]

se deduce que\[\int\left(12 x^{2}-\cos (x)\right) d x=4 x^{3}-\sin (x)+c ,\] donde, como antes,\(c\) es alguna constante.

De nuestras reglas de diferenciación, se deduce fácilmente que

\[\int x^{n} d x=\frac{1}{n+1} x^{n+1}+c\]o cada racional\(n \neq-1,\) y\[\int \sin (x) d x=-\cos (x)+c ,\]\[\int \cos (x) d x=\sin (x)+c ,\]\[\int \sec ^{2}(x) d x=\tan (x)+c ,\]\[\int \csc ^{2}(x) d x=-\csc (x)+c ,\]\[\int \sec (x) \tan (x) d x=\sec (x)+c ,\] y\[\int \csc (x) \cot (x) d x=-\csc (x)+c ,\] donde en cada caso\(c\) representa una constante arbitraria. Obsérvese que la diferenciación del lado derecho de cada uno de los anteriores verifica estos enunciados. Además, si se desprende de nuestro trabajo con derivados que para cualquier función\(f\) y\(g\) y cualquier constante\(k\),\[\int(f(x)+g(x)) d x=\int f(x) d x+\int g(x) d x ,\]\[\int(f(x)-g(x)) d x=\int f(x) d x-\int g(x) d x ,\] y\[\int k f(x) d x=k \int f(x) d x .\]

Ejemplo\(\PageIndex{4}\)

\[\int\left(5 x^{3}-6 x+8\right) d x=\frac{5}{4} x^{4}-3 x^{2}+8 x+c .\]

Ejemplo\(\PageIndex{5}\)

\[\int(\sin (x)-4 \cos (x)) d x=-\cos (x)-4 \sin (x)+c .\]

Ejemplo\(\PageIndex{6}\)

Haciendo un ajuste para la regla de la cadena, vemos que

\[\int \sin (5 x) d x=-\frac{1}{5} \cos (5 x)+c .\]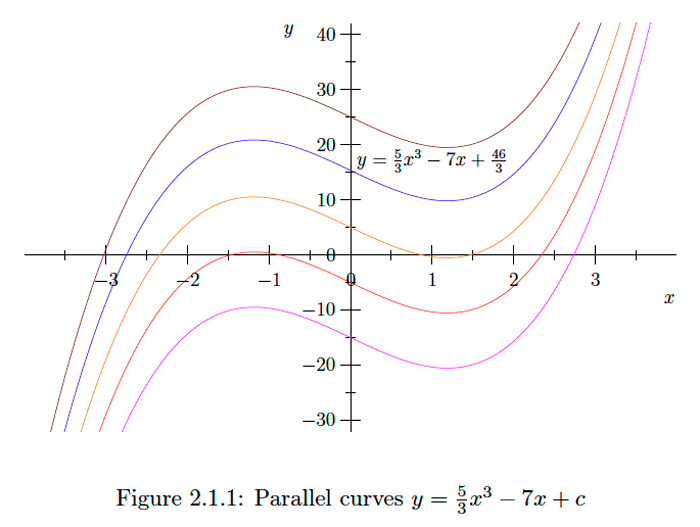

Ejemplo\(\PageIndex{7}\)

Supongamos que deseamos encontrar la integral\(F(x)\) de\(f(x)=5 x^{2}-7\) para la cual\(F(1)=10 .\) Ahora

\[\int\left(5 x^{2}-7\right) d x=\frac{5}{3} x^{3}-7 x+c ,\]así que\[F(x)=\frac{5}{3} x^{3}-7 x+c \] para alguna constante\(c .\) Ahora queremos\[10=F(1)=\frac{5}{3}-7+c ,\] así debemos tener\[c=10+7-\frac{5}{3}=\frac{46}{3} .\] De ahí que la integral deseada es\[F(x)=\frac{5}{3} x^{3}-7 x+\frac{46}{3} .\] Obsérvese que, geométricamente, de la familia de curvas paralelas con ecuaciones de la forma\(y=\frac{5}{3} x^{3}-7 x+c,\) estamos encontrando la que pasa por el punto \((1,10) .\)La Figura 2.1 .1 muestra cinco de tales curvas, con la gráfica de\(F\) en azul.

Ejercicio\(\PageIndex{1}\)

Evaluar cada uno de los siguientes:

\[\begin{array}{ll}{\text { (a) } \int\left(x^{2}+3\right) d x} & {\text { (b) } \int \frac{1}{x^{2}} d x} \\ {\text { (c) } \int(3 \sin (x)-5 \sec (x) \tan (x)) d x} & {\text { (d) } \int 4 \sqrt{x} d x}\end{array} \]

Responder

a)\(\int\left(x^{2}+3\right) d x=\frac{1}{3} x^{3}+3 x+c\)

b)\(\int \frac{1}{x^{2}} d x=-\frac{1}{x}+c\)

c)\(\int(3 \sin (x)-5 \sec (x) \tan (x)) d x=-3 \cos (x)-5 \sec (x)+c\)

d)\(\int 4 \sqrt{x} d x=6 x^{\frac{3}{2}}+c\)

Ejercicio\(\PageIndex{2}\)

Encuentra una integral\(F\) de la\(f(x)=5 x^{4}-4 x\) que satisfaga\(F(2)=12\).

Responder

\(F(x)=x^{5}-2 x^{2}-12\)

Volviendo a nuestro problema original, ahora podemos decir que si\(v(t)\) es, en\(t,\) el momento la velocidad de un objeto que se mueve a lo largo de una línea recta y\(x(t)\) es la posición del objeto en el momento\(t\), entonces

\[x(t)=\int v(t) d t \]No obstante, tenga en cuenta que\((2.1 .16)\) es poco más que una reformulación de\((2.1 .1)\) con nueva notación.

Ejemplo\(\PageIndex{8}\)

Supongamos que la velocidad de un objeto que oscila al final de un resorte es

\[v(t)=-20 \sin (5 t) \text { centimeters / second. } \]Si\(x(t)\) es la posición del objeto en el momento\(t,\) entonces\[x(t)=-\int 20 \sin (5 t) d t=4 \cos (5 t)+c \text { centimeters } \] para alguna constante\(c .\) Si además sabemos que el objeto estaba inicialmente a 4 centímetros del origen, es decir, que\(x(0)=4,\) entonces tendríamos\[4=x(0)=4+c .\] De ahí tendríamos\(c=0,\) y así \[x(t)=4 \cos (5 t) \text { centimeters } \]especifica completamente la posición del objeto en el momento\(t .\)

Ejercicio\(\PageIndex{3}\)

Supongamos que la velocidad de un objeto en el momento\(t\) es\(v(t)=10 \sin (t)\) centímetros por segundo. Encuentra\(x(t),\) la posición del objeto a la hora\(t,\) si es de\(x(0)=\) 10 centímetros.

Responder

\(x(t)=-10 \cos (t)+20\)

2.1.1 El caso de la aceleración constante

Galileo fue el primero en notar que, ignorando los efectos de la resistencia al aire, los objetos en caída libre cerca de la superficie de la tierra caen con aceleración constante. Supongamos que\(x(t), v(t),\) y\(a(t)\) especifique, en\(t,\) el momento, la posición, velocidad y aceleración de un objeto que se mueve a lo largo de una línea recta, y, además, suponga

\[a(t)=g\]para alguna constante\(g\) y todos los valores de\(t .\) Dado que la aceleración es la derivada de la velocidad, se deduce que\[v(t)=\int a(t) d t=\int g d t=g t+c \] para alguna constante\(c .\) Ahora si dejamos que\(v_{0}=v(0),\) la velocidad del objeto en el tiempo\(t=0,\) entonces entonces\[v_{0}=v(0)=c .\] De ahí\[v(t)=g t+v_{0} .\] Siguiente vemos que \[x(t)=\int v(t) d t=\int\left(g t+v_{0}\right) d t=\frac{1}{2} g t^{2}+v_{0} t+c \]para alguna constante\(c .\) Si dejamos que\(x_{0}=x(0),\) la posición del objeto en el momento\(t=0,\) entonces entonces\[x_{0}=x(0)=c .\] De ahí que tengamos\[x(t)=\frac{1}{2} g t^{2}+v_{0} t+x_{0} .\] En el importante caso de un objeto en caída libre cerca de la superficie de la tierra,\(g\) es la aceleración constante debido a la gravedad. Al trabajar en unidades de metros y segundos, y tomando como dirección positiva, tenemos\(g=-9.8\) metros por segundo por segundo, y cuando se trabaja con unidades de pies y segundos\(g=-32\) pies por segundo por segundo. De ahí que en el primer caso,\((2.1 .23)\) se convierta\[x(t)=-4.9 t^{2}+v_{0} t+x_{0}\] y, en el segundo,\((2.1 .23)\) se convierta en\[x(t)=-16 t^{2}+v_{0} t+x_{0}.\]

Ejemplo\(\PageIndex{9}\)

Supongamos que un objeto es arrojado hacia arriba desde lo alto de una torre de 10 metros de altura con una velocidad inicial de 20 metros por segundo. Entonces, usando\((2.1 .24),\) la posición del objeto después de\(t\) segundos es

\[x(t)=-4.9 t^{2}+20 t+10 \text { meters. }\]De ahí que, por ejemplo, ya que el objeto alcanzará su altura máxima cuando sea su velocidad\(0,\) vemos que el objeto alcanza su altura máxima cuando es\[-9.8 t+20=0 ,\] decir, cuando\[t=\frac{20}{9.8} \approx 2.04 \text { seconds. }\] Así el objeto alcanzará una altura máxima de\[x(2.04) \approx-4.9(2.04)^{2}+20(2.04)+10 \approx 30.41 \text { meters. }\]

Ejercicio\(\PageIndex{4}\)

Para un objeto en caída libre cerca de la superficie de Marte,\(g=-3.69\) metros por segundo por segundo. Encuentra la altura máxima que alcanza un objeto lanzado verticalmente al aire desde lo alto de una torre de 10 metros de altura en Marte con una velocidad inicial de 20 metros por segundo.

Responder

64.20 metros