1.2: Definiciones - Números Primos
- Page ID
- 114056
Habrás notado que en la Sección 1.1 se puso muchísimo énfasis en si teníamos definiciones buenas y precisas para las cosas. En efecto, más de una vez se hicieron disculpas por dar definiciones imprecisas o intuitivas. Esto se debe a que, en Matemáticas, las definiciones son nuestro alma. Más que en cualquier otro esfuerzo humano, los matemáticos se esfuerzan por lograr la precisión. Esta precisión viene con un costo — Las matemáticas pueden lidiar solo con el más simple de los fenómenos 1. Para los laicos que piensan que las matemáticas son un tema terriblemente difícil, esa última frase sin duda sonará extraña, pero la mayoría de los matemáticos profesionales estarán asintiendo con la cabeza en este punto. Las preguntas difíciles son tratadas más adecuadamente por los filósofos que por los matemáticos. ¿Un gato tiene alma? Imposible decirlo, porque ninguno de los sustantivos en esa cuestión puede definirse con precisión alguna. ¿Es la raíz cuadrada de\(2\) un número racional? ¡Absolutamente no! El motivo de la certeza que sentimos al responder a esta segunda pregunta es que sabemos precisamente lo que se entiende por las frases “raíz cuadrada de\(2\)” y “número racional”.
A menudo necesitamos abordar primero un tema pensando visual o intuitivamente, pero a la hora de probar nuestras afirmaciones, nada supera el poder de tener las definiciones “correctas” alrededor. Puede ser sorprendente saber que la definición “correcta” a menudo evoluciona a lo largo de los años. Esto sucede por la sencilla razón de que algunas definiciones se prestan más fácilmente a probar aseveraciones. De hecho, suele darse el caso de que las definiciones se inspiran en intentos de probar algo que fracasa. En medio de tal fracaso, no es raro que un Matemático se bame “Si tan sólo la definición de (rellenar el blanco) fuera.”., entonces para darse cuenta de que es posible usar esa definición o una modificación de la misma. ¡Pero! Cuando hay varias definiciones para la misma idea ¡es mejor que estén de acuerdo entre sí!
Considera la definición de un número primo.
Un número primo es un entero positivo, mayor que\(1\), cuyos únicos factores son\(1\) y en sí mismo.
Probablemente escuchaste por primera vez esta definición en la secundaria, si no antes. Es una definición perfectamente válida de lo que significa que un entero sea primo. En matemáticas más avanzadas, se encontró que era necesario definir una noción de primalidad para objetos distintos a los enteros. Resulta que la siguiente declaración es esencialmente equivalente a la definición de “prime” que acabamos de dar (cuando se trata de enteros), pero que se puede aplicar en configuraciones más generales.
Un primo es una cantidad\(p\) tal que cada vez que\(p\) es un factor de algún producto\(ab\), entonces o\(p\) es un factor de\(a\) o\(p\) es un factor de\ (b\ |).
El número no\(1\) se considera primo. ¿\(1\)Satisface la definición anterior?
Si vas a estudiar Teoría de Números o Álgebra Abstracta verás cómo es necesario modificar la definición alternativa que hemos dado para que (por ejemplo)\(1\) no se cuente como primo. El arreglo no es enormemente complicado (pero es un poco complicado) y está un poco más allá de nuestro alcance en estos momentos.
A menudo, es el caso de que podemos formular muchas definiciones equivalentes para algún concepto. Cuando esto sucede, puede encontrarse con la abreviatura TFAE, que significa “Los siguientes son equivalentes”. Una prueba TFAE consiste en mostrar que una serie de declaraciones diferentes definen realmente el mismo concepto.
Dado que hemos estado discutiendo primos en esta sección (principalmente como ejemplo de un concepto con más de una definición equivalente), este parece un tiempo razonable para hacer algunas exploraciones relativas a los números primos. Comenzaremos en el siglo III a.C. Eratóstenes de Cirene fue un matemático y astrónomo griego que es recordado hasta nuestros días por sus muchos logros. Fue bibliotecario en la gran biblioteca de Alejandría. Hizo mediciones de la circunferencia de la Tierra y las distancias del Sol y la Luna que fueron notablemente precisas, pero probablemente su logro más recordado es el método de “tamiz” para encontrar primos. En efecto, el tamiz de Eratóstenes sigue siendo de importancia en la investigación matemática. Básicamente, el método sieve consiste en crear una lista muy larga de números naturales y luego tachar todos los números que no son primos (un entero positivo que no es\(1\), y no es primo se llama compuesto). Este proceso se lleva a cabo por etapas. Primero, hacemos un círculo\(2\) y luego tachamos cada número que tiene\(2\) como factor, por lo tanto, nos hemos identificado\(2\) como el primer número primo y eliminado un montón de números que no son primos. El primer número que no ha sido eliminado en esta etapa es\(3\), lo rodeamos (indicando que\(3\) es el segundo número primo) y luego tachamos cada número que tiene\(3\) como factor. ¡Tenga en cuenta que algunos números (por ejemplo,\(6\) y\(12\)) se habrán tachado más de una vez! En la tercera etapa del proceso de tamiz, hacemos un círculo\(5\), que es el número más pequeño que aún no se ha tachado, para luego tachar todos los múltiplos de\(5\). Las tres primeras etapas en el método de tamiz se muestran en la Figura\(1.2.1\).
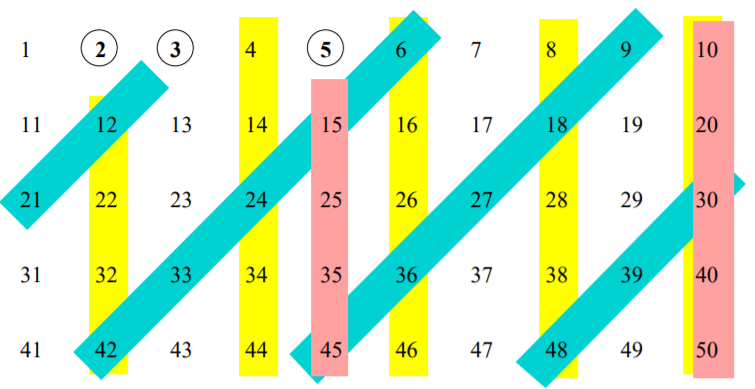
Es interesante señalar que el tamiz nos da un medio para encontrar todos los primos hasta\(p^2\) usando los primos hasta (pero sin incluir)\(p\). Por ejemplo, para encontrar todos los primos menos que\(13^2 = 169\), solo necesitamos usar\(2\),\(3\),\(5\),\(7\) y\(11\) en el tamiz.
A pesar de que uno puede encontrar primos usando este sencillo método mecánico, la forma en que los números primos se distribuyen entre los enteros es muy errática. Casi cualquier afirmación que pretenda mostrar cierta regularidad en la distribución de los primos resultará ser falsa. Aquí hay dos conjeturas falsas con respecto a los números primos.
Siempre que\(p\) es un número primo, también\(2^p − 1\) es primo.
El polinomio\(x^2 − 31x + 257\) evalúa a un número primo siempre que\(x\) sea un número natural.
En los ejercicios de esta sección, se le pedirá que explore más a fondo estas declaraciones.
Los números primos actúan como bloques de construcción multiplicativos para el resto de los números enteros. Cuando desmontamos un entero en sus bloques de construcción, estamos encontrando la factorización prima de ese número. Las factorizaciones Prime son únicas. Es decir, un número es primo o tiene factores primos (posiblemente elevados a varios poderes) que se determinan de manera única, excepto que pueden ser reordenados.
A continuación se muestra una tabla que contiene todos los primos que son menores que\(5000\). ¡Estudia esta mesa y descubre el secreto de su compacidad!
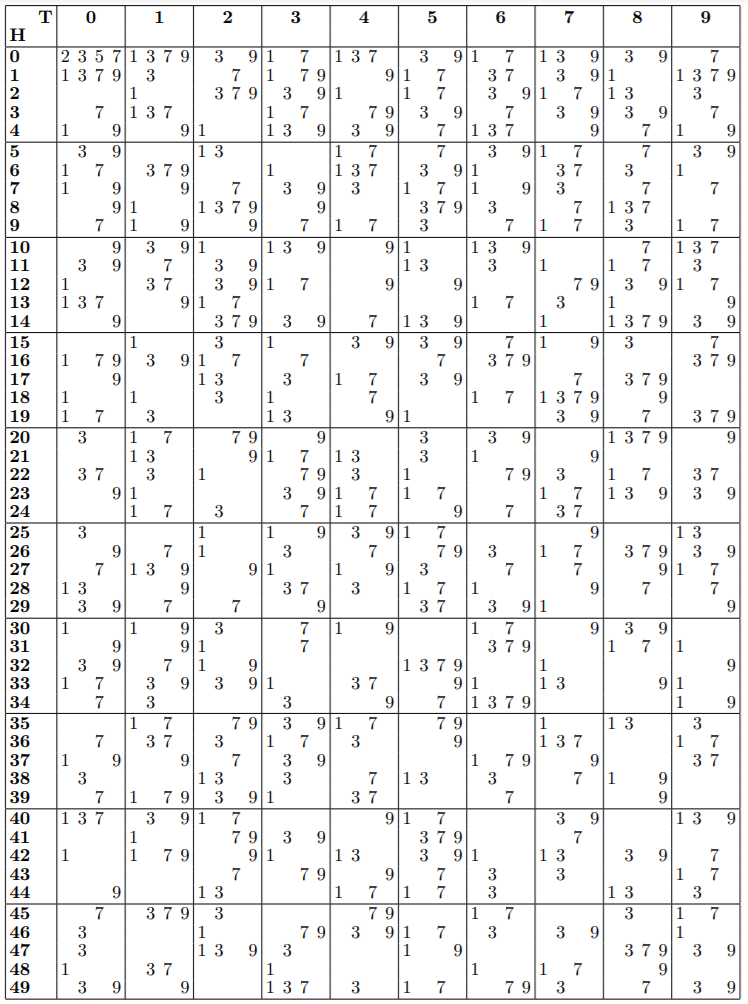
Ejercicios
Encuentra las factorizaciones primos de los siguientes enteros.
- 105
- 414
- 168
- 1612
- 9177
Usa el tamiz de Eratóstenes para encontrar todos los números primos hasta\(100\).
\[ \begin{array} a1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 \\ 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20\\ 21 & 22 & 23 & 24 & 25 & 26 & 27 & 28 & 29 & 30\\ 31 & 32 & 33 & 34 & 35 & 36 & 37 & 38 & 39 & 40 \\ 41 & 42 & 43 & 44 & 45 & 46 & 47 & 48 & 49 & 50 \\ 51 & 52 & 53 & 54 & 55 & 56 & 57 & 58 & 59 & 60 \\ 61 & 62 & 63 & 64 & 65 & 66 & 67 & 68 & 69 & 70 \\ 71 & 72 & 73 & 74 & 75 & 76 & 77 & 78 & 79 & 80 \\ 81 & 82 & 83 & 84 & 85 & 86 & 87 & 88 & 89 & 90 \\ 91 & 92 & 93 & 94 & 95 & 96 & 97 & 98 & 99 & 100 \\ \end{array} \]
¿Cuál sería el prime más grande con el que se cribaría para encontrar todos los primos hasta 400?
Caracterizar las factorizaciones primos de números que son cuadrados perfectos.
Complete la siguiente tabla que está relacionada con Conjetura\(1.2.1\).
| \(p\) | \(2^p - 1\) | prime? | factores |
| \(2\) | \(3\) | si | \(1\)y\(3\) |
| \(3\) | \(7\) | si | \(1\)y\(7\) |
| \(5\) | \(31\) | si | |
| \(7\) | \(127\) | ||
| \(11\) |
Encuentra un contraejemplo para Conjetura\(1.2.2\)
Usa la segunda definición de “prime” para ver que no\(6\) es primo. Es decir, encontrar dos números (el a y b que aparecen en la definición) tal que no\(6\) sea un factor de ninguno, sino que sea un factor de su producto.
Usa la segunda definición de “prime” para mostrar que no\(35\) es primo.
Una conjetura famosa que se piensa que es cierta (pero de la que no se conoce ninguna prueba) es la conjetura de Twin Prime. Se dice que un par de primos son gemelos si difieren en\(2\). Por ejemplo,\(11\) y\(13\) son primos gemelos, como son\(431\) y\(433\). La conjetura de Twin Prime afirma que hay un número infinito de tales gemelos. Trate de llegar a un argumento de por qué\(3\),\(5\) y\(7\) son los únicos trillizos primos.
Otra conjetura famosa, también pensada como cierta —pero aún no probada, es la conjetura de Goldbach. La conjetura de Goldbach establece que cada número par mayor que\(4\) es la suma de dos primos impares. Hay una función\(g(n)\), conocida como la función Goldbach, definida en los enteros positivos, que da el número de diferentes formas de escribir un número dado como la suma de dos primos impares. Por ejemplo,\(g(10) = 2\) ya que\(10 = 5 + 5 = 7 + 3\). Así, otra versión de la conjetura de Goldbach es que\(g(n)\) es positiva siempre que n sea un número par mayor que\(4\).
Gráfica\(g(n)\) para\(6 ≤ n ≤ 20\).


