1.4: Definiciones de la Teoría de Números Elementales
- Page ID
- 114048
1.4.1: Par e Impar
Si divide un número por\(2\) y sale par (es decir, sin resto) se dice que el número es par. Entonces la palabra incluso se relaciona con división. Resulta que el concepto incluso se entiende mejor a través del pensamiento sobre la multiplicación.
Un entero\(n\) es incluso exactamente cuando hay un entero\(m\) tal que\(n = 2m\).
Debe tener en cuenta que hay una especie de “calle de dos vías” de calidad en esta definición —de hecho con la mayoría, si no todas, las definiciones. Si un número es par, entonces se nos garantiza la existencia de otro entero medio de grande. Por otro lado, si podemos demostrar que existe otro entero medio tan grande, entonces sabemos que el número original es par. Esta bidirectividad significa que la definición es lo que se conoce como un bicondicional, un concepto que volveremos a examinar en la Sección 2.2.
Mucha gente no cree que eso\(0\) deba contarse como un número par. Ahora que estamos armados con una definición precisa, podemos responder a esta pregunta fácilmente. ¿Hay un entero\(x\) tal que\(0 = 2x\)? ¡Ciertamente! déjalo ser\(x\) también\(0\). (Observe que en la definición, no se dijo nada al respecto\(m\) y de\(n\) ser distintos el uno del otro.)
Un entero es impar si no es par. Es decir, entre los enteros, sólo hay dos posibilidades: par o impar. También podemos definir rareza sin hacer referencia a “par”.
Un entero\(n\) es impar exactamente cuando hay un entero\(m\) tal que\(n = 2m + 1\).
1.4.2:\(n\) Notación decimal y base
También se pueden identificar números pares considerando su representación decimal. Recordemos que cada dígito en la representación decimal de un número tiene un valor que depende de su posición. Por ejemplo, el número\(3482\) realmente significa\(3 · 10^3 + 4 · 10^2 + 8 · 10^1 + 2 · 10^0\). Esto también se conoce como notación de lugar. El hecho de que usemos los poderes de\(10\) en nuestro lugar la notación probablemente se deba a que la mayoría de los humanos tienen\(10\) dedos. Es posible utilizar cualquier número en lugar de\(10\). En Ciencias de la Computación existen\(3\) otras bases de uso común:\(2\),\(8\) y\(16\) — éstas se conocen (respectivamente) como notación binaria, octal y hexadecimal. Al denotar un número usando alguna base distinta a\(10\), se acostumbra agregar un subíndice que indique la base. Entonces, por ejemplo,\(1011_2\) es notación binaria que significa\(1 · 2^3 + 0 · 2^2 + 1 · 2^1 + 1 · 2^0\) o\(8 + 2 + 1 = 11\). No importa qué base estemos usando, el dígito más a la derecha del número multiplica la base elevada a la\(0\) -ésima potencia. Cualquier número elevado a la potencia\(0\) -ésima es\(1\), y el dígito más a la derecha se conoce en consecuencia como el dígito de unidades. Ahora estamos preparados para dar algunas declaraciones que equivalen a nuestra definición de par. Estas afirmaciones realmente no merecen la designación de “teorema”, son consecuencias inmediatas de la definición.
Un entero es incluso si el dígito de unidades en su representación decimal es uno de\(0\),\(2\),\(4\),\(6\) o\(8\).
Un entero es incluso si el dígito de unidades en su representación binaria es\(0\).
Para ciertos problemas es natural utilizar algún sistema notacional particular. Por ejemplo, el último teorema tendería a indicar que los números binarios son útiles en problemas que tratan con pares e impares. Dado que hay muchas notaciones diferentes de las que disponemos, obviamente es deseable tener medios a nuestra disposición para convertir entre ellas. Es posible desarrollar reglas generales para convertir un número base en un\(a\) número base (donde a y b son arbitrarios) pero en realidad es más conveniente elegir una base “estándar” (y como somos humanos usaremos base-\(10\)) y desarrollar métodos para convertir entre una base arbitraria\(b\) y el “estándar”. Imagínese que en un futuro no muy lejano necesitamos convertir algunos números del\(7\) sistema base utilizado por los Amoebazoides de siete lóbulos de Epsilon Eridani III al\(12\) esquema base favorecido por los Dodecatones de Alfa-Centauri IV. Necesitaremos un procedimiento para convertir base\(7\) a base\(10\) y otro procedimiento para convertir de base\(10\) a base\(12\). En el episodio de School House Rock “Little Twelve Toes” describen\(12\) la numeración base de una manera que es comprensible para los niños de primaria —los dígitos que utilizan son\(\{1, 2, 3, 4, 5, 6, 7, 8, 9, δ, \epsilon \}\), los dos últimos dígitos (que se pronuncian “dec” y “el”) son necesarios ya que necesitamos símbolos únicos para el cosas que habitualmente denotamos usando\(10\) y\(11\).
Convertir de alguna otra base a decimal es fácil. Simplemente usa la definición de notación de lugar. Por ejemplo, para encontrar lo que\(451663_7\) representa en decimal, simplemente escriba
\(4·7^5+5·7^4+1·7^3+6·7^2+6·7+3 = 4·16807+5·2401+1·343+6·49+6·7+3 = 79915.\)
(Todo en la línea anterior se puede interpretar como un\(10\) número base, y no son necesarios subíndices para base-\(10\).)
Convertir de decimal a alguna otra base es más difícil. Existe un algoritmo llamado “división repetida” que exploraremos un poco en los ejercicios para esta sección. Por el momento, basta con verificar que también\(3δ2 \epsilon 7_{12}\) sea una representación del número escrito más convencionalmente como\(79915\).
1.4.3: Divisibilidad
La noción de ser incluso tiene una generalización obvia. Supongamos que preguntamos si\(3\) se divide equitativamente en un número dado. Presumiblemente, podríamos hacer una definición de lo que significaba ser tres pares, pero en lugar de hacerlo (o dedicarnos a más punnery) pasaremos a una definición general. Necesitamos una notación para la situación en la que un número se divide uniformemente en otro. Hay muchas maneras de describir esta situación en inglés, pero esencialmente solo una en “matemáticas”, usamos una barra vertical, no una barra de fracción. De hecho, la diferencia entre esta barra vertical y el símbolo de fracción (\(|\)versus\(/\)) necesita ser fuertemente enfatizada. La barra vertical cuando se coloca entre dos números es un símbolo que hace la pregunta “¿El primer número se divide uniformemente (es decir, sin resto) en el segundo?” Por otro lado la barra de fracciones te pide que realmente lleves a cabo alguna división. El valor de\(2 | 5\) es falso, mientras que el valor de\(2/5\) es\(.4\).
Como fue el caso al definir par, resulta que lo mejor es pensar en la multiplicación, no en la división, a la hora de hacer una definición formal de este concepto. Dados dos enteros cualesquiera\(n\) y\(d\) definimos el símbolo\(d|n\) por
\(d|n\)exactamente cuando\(∃k ∈ Z\) tal que\(n = kd\)
En lenguaje hablado, el símbolo se\(d|n\) puede traducir de varias maneras:
- \(d\)es un divisor de\(n\).
- \(d\)se divide de\(n\) manera uniforme.
- \(d\)es un factor de\(n\).
- \(n\)es un múltiplo entero de\(d\).
Si bien, con mucho, la forma más popular de expresar este concepto es simplemente decir “\(d\)divide”\(n\).
1.4.4: Piso y Techo
Supongamos que hay un elevador con capacidad de\(1300\) libras. Un grupo numeroso de hombres que todos pesan alrededor de\(200\) libras quieren ascender en él. ¿Cuántos deben montar a la vez? Esto es sólo un problema de división,\(1300/200\) da\(6.5\) hombres deben montar juntos. Bueno, obviamente poner a media persona en un elevador es una mala idea — ¿deberíamos simplemente redondear y dejar\(7\) ir juntos? ¡No si la clasificación de capacidad en\(1300\) libras no tiene un margen de seguridad! Este es un ejemplo del tipo de problema en el que se utiliza la función floor. La función floor toma un número real como entrada y devuelve el siguiente entero inferior.
Supongamos que después de una fiesta tenemos botellas de cerveza\(43\) sin abrir. Nos gustaría guardarlos en contenedores que contienen\(12\) botellas cada uno. ¿Cuántos contenedores necesitaremos? Nuevamente, esto es simplemente un problema de división\(– 43/12 = 3.58333\). Entonces necesitamos\(3\) cajas y otras\(7\) doceavos de caja. Obviamente, realmente necesitamos\(4\) cajas — al menos una tendrá algún espacio sin usar en ella. En este tipo de situaciones, estamos lidiando con la función de techo. Dado un número real, la función de techo lo redondea hasta el siguiente entero.
Ambas funciones se denotan usando símbolos que se parecen mucho a las barras de valor absoluto. La diferencia radica en algunos pequeños trazos horizontales.
Si\(x\) es un número real, se denota su piso\(\lfloor x \rfloor\), y se denota su techo\(\lceil x \rceil\). Aquí están las definiciones formales:
\(y = \lfloor x \rfloor\)exactamente cuándo\(y ∈ Z\) y\(y ≤ x < y + 1\).
\(y = \lceil x \rceil\)exactamente cuándo\(y ∈ Z\) y\(y − 1 < x ≤ y\).
Básicamente, la definición de piso dice que\(y\) es un entero que es menor o igual a\(x\), pero\(y + 1\) definitivamente excede\(x\). La definición de techo puede parafrasearse de manera similar.
1.4.5: Div y mod
En la siguiente sección, discutiremos el llamado algoritmo de división, ¡esto puede ser un exceso de matar ya que ciertamente ya sabes cómo hacer división! De hecho, en Estados Unidos, la división larga generalmente se estudia primero en la segunda mitad de la escuela primaria, y los problemas de división que no involucran un resto pueden encontrarse ya en el primer grado. Sin embargo, vamos a discutir este proceso con sórdido detalle porque nos da un buen escenario en el que demostrar declaraciones relativamente fáciles. Supongamos que está configurando un problema de división larga en el que el entero\(n\) está siendo dividido por un divisor positivo\(d\). (Si quieres dividir por un número negativo, simplemente divídalo por el número positivo correspondiente y luego lanza un signo menos adicional al final).
\( \;\;\;\underline{\;\;q\;\;\;} \\ d| \;\;n \\ \;\;\;\;... \\ \;\;\underline{\;\;\;\;\;\;\;\;} \\ \;\;\;\;\;r\)
Recordemos que la respuesta consta de dos partes, un cociente\(q\) y un resto\(r\). Por supuesto,\(r\) puede ser cero, pero también, el más grande\(r\) puede ser es\(d − 1\). La afirmación de que esta respuesta existe de manera única se conoce como el teorema del cociente-resto:
Dados enteros\(n\) y\(d > 0\), hay enteros únicos\(q\) y\(r\) tal que\(n = qd + r\) y\(0 ≤ r < d\).
Las palabras “div” y “mod” que aparecen en el título de esta subsección proporcionan taquigrafía matemática para\(q\) y\(r\). A saber, “\(n \text{ mod } d\)” es una forma de expresar el resto\(r\), y “\(n \text{ div } d\)” es una forma de expresar el cociente\(q\).
Si dos enteros,\(m\) y\(n\), dejan el mismo resto cuando los divide por\(d\), decimos que son congruentes módulo\(d\). Se podría expresar esto por escrito\(n \text{ mod } d = m \text{ mod } d \), pero usualmente adoptamos una notación taquigráfica
\[n ≡ m (\text{mod } d).\]
Si uno está en un contexto en el que está completamente claro lo que\(d\) es, es aceptable simplemente escribir\(n ≡ m\).
La operación “\(\text{mod}\)” se usa bastante en matemáticas. Cuando hacemos cálculos módulo algún número\(d\), (esto se conoce como “aritmética modular” o, a veces, “aritmética de reloj”) algunas propiedades muy bonitas de “\(\text{mod}\)” vienen muy bien
\[x + y \text{ mod } d = (x \text{ mod } d + y \text{ mod } d) \text{ mod } d\]
y
\[x · y \text{ mod } d = (x \text{ mod } d · y \text{ mod } d) \text{ mod } d.\]
Estas reglas significan que podemos hacer primero las operaciones, luego reducir la respuesta\(\text{mod } d\) o podemos hacer la reducción\(\text{mod } d\) primero y luego hacer las operaciones (aunque tal vez tengamos que hacer una ronda más de reducción\(\text{mod } d\)).
Por ejemplo, si estamos trabajando\(\text{mod } 10\), y queremos calcular\(87·96 \text{ mod } 10\), en cambio podemos simplemente calcular\(7 · 6 \text{ mod } 10\), que es\(2\).
1.4.6: Coeficientes binomiales
Un “binomio” es un polinomio con\(2\) términos, por ejemplo\(x + 1\) o\(a + b\). Los números que aparecen como coeficientes cuando uno eleva un binomio a alguna potencia son, sorprendentemente, conocidos como coeficientes binomiales
Echemos un vistazo a los primeros varios poderes de\(a + b\).
\[\begin{array} (a + b)^0 &= 1 \\ (a + b)^1 &= a + b \\ (a + b)^2 &= a^2 + 2ab + b^2 \end{array}\]
Para ir mucho más allá de la segunda potencia requiere un poco de trabajo, pero prueba lo siguiente
Multiplicar\((a+b)\) y\((a^2 + 2ab+b^2)\) con el fin de determinar\((a+b)^3\). Si te sientes a la altura, multiplica los\((a^2+2ab+b^2)\) tiempos a sí mismo para poder encontrar\((a+b)^4\).
Ya que nos interesan los coeficientes de estos polinomios, es importante señalar que si no aparece ningún coeficiente frente a un término eso significa que el coeficiente es\(1\).
Estos coeficientes binomiales se pueden colocar en una disposición conocida como triángulo 1 de Pascal, que proporciona una manera conveniente de calcular pequeños coeficientes binomiales
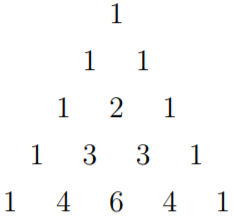
Observe que en el triángulo hay un borde en ambos lados que contiene 1's y que los números en el interior del triángulo son la suma de los dos números por encima de ellos. Puedes usar estos hechos para extender el triángulo.
Agrega las siguientes dos filas al triángulo Pascal en la Figura\(1.4.1\).
Los coeficientes binomiales se denotan usando un símbolo de aspecto algo extraño. Se denota el número en la posición\(k\) -ésima en el número\(n\) de fila del triángulo\(\binom{n}{k}\). Esto se parece un poco a una fracción, pero falta la barra de fracciones. ¡No pongas uno! Se supone que está desaparecida. En inglés hablado, dices “\(n\)elige\(k\)” cuando te encuentras con el símbolo\(\binom{n}{k}\).
Hay una fórmula para los coeficientes binomiales —lo cual es agradable. De lo contrario necesitaríamos completar un triángulo Pascal bastante enorme para poder calcular algo así como\(\binom{52}{5}\). La fórmula implica notación factorial. Solo para estar seguros de que todos estamos en la misma página, definiremos factoriales antes de continuar.
El símbolo para las factoriales es un signo de exclamación que sigue a un número. Esto es solo una manecilla corta para expresar el producto de todos los números hasta uno dado. Por ejemplo\(7!\) significa\(1 · 2 · 3 · 4 · 5 · 6 · 7\). Por supuesto, realmente no hay necesidad de escribir la inicial\(1\) — también, por alguna razón la gente suele escribir el producto en orden decreciente\((7! = 7 · 6 · 5 · 4 · 3 · 2)\).
La fórmula para un coeficiente binomial es
\[\binom{n}{k} = \dfrac{n!}{k! · (n − k)!} \]
Por ejemplo
\[\binom{5}{3} = \dfrac{5!}{3! · (5 − 3)!} = \dfrac{1 · 2 · 3 · 4 · 5}{ (1 · 2 · 3) · (1 · 2)} = 10 \]
Un ejemplo un poco más complicado (y uno que a los apostadores les gusta) es
\[\begin{array} \binom{52}{5} &= \dfrac{52!}{5! · (52 − 5)!} \\ &= \dfrac{1 · 2 · 3 · · · · 52}{(1 · 2 · 3 · 4 · 5) · (1 · 2 · 3 · · · · 47)} \\ &= \dfrac{48 · 49 · 50 · 51 · 52}{1 · 2 · 3 · 4 · 5} \\ &= 2598960. \end{array}\]
La razón por la que un jugador podría estar interesado en el número que acabamos de calcular es que los coeficientes binomiales hacen algo más que darnos los coeficientes en la expansión de un binomio. También se pueden usar para calcular cuántas formas se puede elegir un subconjunto de un tamaño dado de un conjunto. Así\(\binom{52}{5}\) es el número de formas en que uno puede obtener una mano de\(5\) cartas de una baraja de\(52\) cartas.
Hay siete días en una semana. De cuántas maneras se puede elegir un conjunto de tres días (por semana)
Ejercicios:
Un entero\(n\\) es doblemente incluso si es par, y el entero\(m\) garantizado que existe porque\(n\) es par es par en sí mismo. ¿\(0\)Es doble par? ¿Cuáles son los primeros enteros\(3\) positivos, dobles pares?
Dividir un entero por dos tiene una interpretación interesante cuando se utiliza la notación binaria: simplemente desplaza los dígitos hacia la derecha. Así,\(22 = 10110_2\) cuando se divide por dos da\(1011_2\) cuál es\(8 + 2 + 1 = 11\). ¿Cómo se puede reconocer un entero doble par a partir de su representación binaria?
La representación octal de un entero utiliza potencias de notación\(8\) in place. Los dígitos de un número octal van desde\(0\) hasta\(7\), uno nunca ve\(8\)'s o\(9\)'s. ¿Cómo representarías\(8\) y\(9\) como números octales? ¿Qué número octal viene inmediatamente después\(777_8\)? ¿Qué número (decimal) es\(777_8\)?
Un método para convertir de decimal a alguna otra base se llama división repetida. Uno divide el número por la base y registra el resto; uno luego divide el cociente obtenido por la base y registra el resto. Continuar dividiendo los cocientes sucesivos por la base hasta que el cociente sea menor que la base. Convertir\(3267\) a base-\(7\) usando división repetida. Verifique su respuesta usando el significado de notación de\(7\) lugar base. (Por ejemplo\(54321_7\) significa\(5 · 7^4 + 4 · 7^3 + 3 · 7^2 + 2 · 7^1 + 1 · 7^0\).)
Indicar un teorema sobre la representación octal de números pares.
En la notación hexadecimal (base\(16\)) uno necesita\(16\) “dígitos”, los dígitos ordinarios se utilizan para\(0\) a través\(9\), y las letras\(\text{A}\) a través\(\text{F}\) se utilizan para dar símbolos individuales para\(10\) a través\(15\). Los primeros números\(32\) naturales en hexadecimal son:
\(1,2,3,4,5,6,7,8,9,\text{A},\text{B},\text{C},\text{D},\text{E},\text{F},10,11,12,13,14,15,16,17,18,19,1\text{A},1\text{B},1\text{C},1\text{D},1\text{E},1\text{F},20\).
Escriba los siguientes números\(10\) hexadecimales después\(\text{AB}\).
Para la conversión entre las tres bases utilizadas con mayor frecuencia en Ciencias de la Computación podemos tomar binario como base “estándar” y convertir usando una tabla de consulta. Cada dígito octal corresponderá a un triple binario, y cada dígito hexadecimal corresponderá a una\(4\) -tupla de números binarios. Complete las siguientes tablas. (Como cheque, la\(4\) -tupla junto a\(A\) en la tabla para hexadecimal debería ser\(1010\) — lo cual es agradable ya que\(A\) es realmente\(10\) así si lees eso como “diez diez” es una buena ayuda para la memoria.)
| octal | binario |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
| hexadecimal | binario |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| \(\text{A}\) | |
| \(\text{B}\) | |
| \(\text{C}\) | |
| \(\text{D}\) | |
| \(\text{E}\) | |
| \(\text{F}\) |
Usa las tablas del problema anterior para realizar las siguientes conversiones.
- Convertir\(757_8\) a binario.
- Convertir\(1007_8\) a hexadecimal.
- Convertir\(100101010110_2\) a octal.
- Convertir\(1111101000110101_2\) a hexadecimal.
- Convertir\(FEED_{16}\) a binario.
- Convertir\(FFFFFF_{16}\) a octal.
Pruebe las siguientes conversiones entre varios sistemas numéricos:
- Convertir\(30\) (base\(10\)) a binario.
- Convertir\(69\) (base\(10\)) a base\(5\).
- Convertir\(12223\) a binario.
- Convertir\(12347\) a base\(10\).
- Convertir\(EEED_{15}\) a base\(12\). (Usar\(\{1, 2, 3 . . . 9, d, e\}\) como los dígitos en la base\(12\).)
- Convertir\(6789\) a hexadecimal.
Es un hecho bien conocido que si un número es divisible por\(3\), entonces\(3\) divide la suma de los dígitos (decimales) de ese número. ¿Este resultado es cierto en base\(7\)? ¿Crees que este resultado es cierto en alguna base?
Supongamos que\(340\) libras de arena deben colocarse en bolsas que tengan una capacidad de\(50\) libra. Escriba una expresión usando notación de piso o techo para el número de bolsas requeridas.
¿Verdadero o falso?
\(\lfloor \dfrac{n}{d} \rfloor < \lceil \dfrac{n}{d} \rceil \)
para todos los enteros\(n\) y\(d > 0\). Respaldar su reclamo.
¿Cuál es el valor de\(\lceil π \rceil^2 − \lceil π^2 \rceil\)?
Asumiendo los símbolos\(n\)\(d\),,\(q\) y\(r\) tienen significados como en el teorema del cociente-resto (Teorema\(1.4.3\)). Escribir expresiones para\(q\) y\(r\), en términos\(n\) y\(d\) usando notación de piso y/o techo.
Calcula las siguientes cantidades:
- \(3 \text{ mod } 5\)
- \(37 \text{ mod } 7\)
- \(1000001 \text{ mod } 100000\)
- \(6 \text{ div } 6\)
- \(7 \text{ div } 6\)
- \(1000001 \text{ div } 2\)
Calcular los siguientes coeficientes binomiales:
- \(\binom{3}{0}\)
- \(\binom{7}{7}\)
- \(\binom{13}{5}\)
- \(\binom{13}{8}\)
- \(\binom{52}{7}\)
Una heladería vende los siguientes sabores: chocolate, vainilla, fresa, café, nuez de mantequilla, chispas de chocolate a la menta y frambuesa. ¿Cuántos cuencos diferentes de helado —con tres bolas— pueden hacer?


