1.5: Algunos algoritmos de la teoría elemental de números
- Page ID
- 114055
Un algoritmo es simplemente un conjunto de instrucciones claras para lograr alguna tarea. El matemático y astrónomo persa Al-Khwarizmi 1 fue un erudito en la Casa de la Sabiduría en Bagdad que vivió en los\(9^{\text{th}}\) siglos\(8^{\text{th}}\) y d.C. Es recordado por su tratado de álgebra Hisab al-jabr w'al-muqabala del que derivamos la misma palabra” álgebra”, y un texto sobre el esquema de numeración indoárabe.
Al-Khwarizmi también escribió un tratado sobre números indoarábigos. El texto árabe se pierde pero una traducción latina, Algoritmi de numero Indorum (en inglés Al-Khwarizmi sobre el arte hindú de Reckoning) dio origen a la palabra algoritmo derivado de su nombre en el título. [12]
Si bien el estudio de algoritmos es más propiamente una asignatura dentro de las Ciencias de la Computación, un estudiante de Matemáticas puede obtener un beneficio considerable de ella.
Existe una gran diferencia entre una descripción de algoritmo destinada al consumo humano y una destinada a una computadora 2. Las dos formas legibles por humanos favorecidas para describir algoritmos son pseudocódigo y diagramas de flujo. El primero está basado en texto y el segundo es visual. Hay muchos módulos diferentes a partir de los cuales se pueden construir estructuras algorítmicas: bucles for-next, loops do-while, sentencias if-then, declaraciones goto, estructuras de cambio de mayúsculas y minúsculas, etc. Usaremos un subconjunto mínimo de las opciones disponibles.
- Declaraciones de asignación
- Sentencias de control de IF y luego
- Declaraciones Goto
- Regreso
Tomamos la opinión de que un algoritmo es algo así como una función, toma para su entrada una lista de parámetros que describen un caso particular de algún problema general, y produce como salida una solución a ese problema. (Cabe señalar que existen otras posibilidades —algunos programas requieren que la variable en la que se va a colocar la salida se los entregue como parámetro de entrada, otros no tengan salida específica, su propósito se logra como un efecto secundario.) El intermediario entre entrada y salida son las propias instrucciones del algoritmo y un conjunto de las llamadas variables locales que se utilizan mucho de la manera en que se usa el papel de desecho en un cálculo manual; en ellas se escriben cálculos intermedios, pero se desechan una vez calculada la respuesta final.
Las declaraciones de asignación nos permiten hacer todo tipo de operaciones aritméticas (o más bien pensar en este tipo de operaciones como atómicas). En realidad incluso un procedimiento simple como sumar dos números requiere de una especie de algoritmo, evitaremos un nivel de detalle tan fino. Las asignaciones consisten en evaluar alguna fórmula (posiblemente bastante complicada) en las entradas y variables locales y asignar ese valor a alguna variable local. Los dos usos de la frase “variable local” en la frase anterior no necesitan ser distintos, por lo que\(x = x + 1\) es una cesión perfectamente legal.
Si entonces las declaraciones de control son tomadores de decisiones. Primero calculan una expresión booleana (esto es solo una forma elegante de decir algo que es verdadero o falso), y envían el flujo del programa a diferentes ubicaciones dependiendo de ese resultado. Un pequeño ejemplo servirá de ilustración. Supongamos que en el cuerpo de un algoritmo deseamos verificar si\(2\) las variables,\(x\) y\(y\) son iguales, y si lo son, incrementar\(x\) por\(1\). Esto se ilustra en la Figura\(1.5.1\) tanto en pseudocódigo como en un diagrama de flujo.
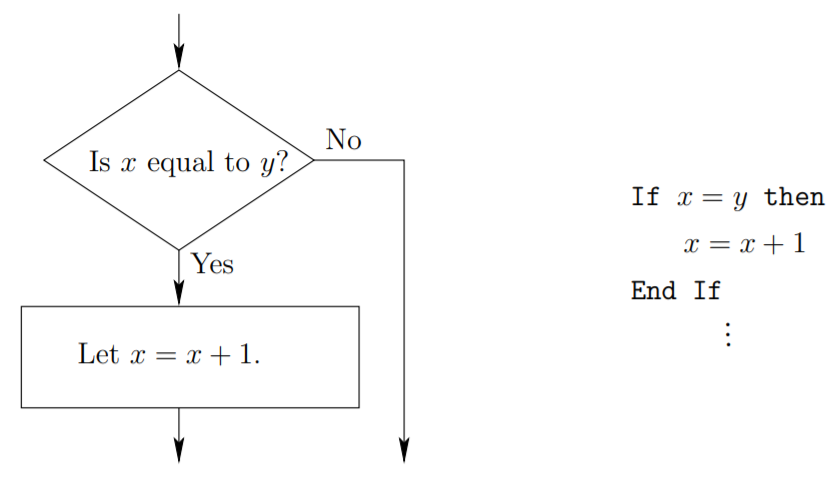
Observe el uso de sangría en el ejemplo de pseudocódigo para indicar las sentencias que se ejecutan si la expresión booleana es verdadera. Estos ejemplos también resaltan la diferencia entre los dos sentidos que tiene la palabra “igual” (y el símbolo\(=\)). En la expresión booleana, el sentido es el de probar la igualdad, en las declaraciones de asignación (como su nombre lo indica) se está haciendo una asignación. En muchos lenguajes de programación, esta distinción se hace explícita, por ejemplo en el lenguaje C las pruebas de igualdad se realizan a través del símbolo “\(==\)” mientras que la asignación se realiza usando un solo signo igual (\(=\)). En Matemáticas el signo igual suele indicar pruebas de igualdad, cuando se desea el sentido de asignación la palabra “dejar” generalmente precederá a la igualdad.
Si bien esta breve introducción a los medios de notación de algoritmos no es de ninguna manera completa, es de esperar que sea suficiente para nuestro propósito, que es únicamente introducir dos algoritmos que son importantes en la teoría de números elementales. El algoritmo de división, como se presenta aquí, es simplemente una versión explícita del proceso que se sigue para calcular un cociente y un resto usando división larga. El procedimiento que damos es inusualmente ineficiente —con muy poco pensamiento se podría idear un algoritmo que produzca la respuesta deseada usando muchas menos operaciones—, sin embargo, el punto principal aquí es simplemente mostrar que la división se puede lograr por medios esencialmente mecánicos. El algoritmo euclidiano es mucho más interesante tanto desde una perspectiva teórica como práctica. El algoritmo euclidiano calcula el mayor divisor común (\(\text{gcd}\)) de dos enteros. El\(\text{gcd}\) de dos números\(a\) y\(b\) se denota\(\text{gcd}(a, b)\) y es el entero más grande que divide ambos\(a\) y\(b\) uniformemente.
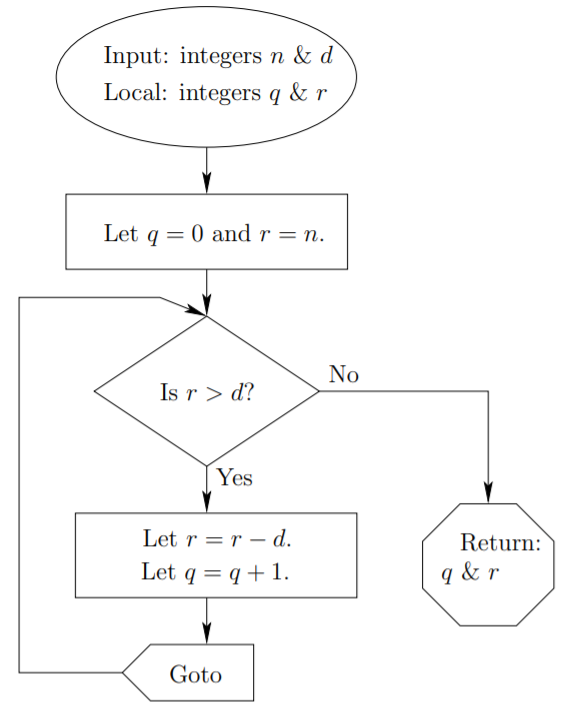
Un esquema de pseudocódigo del algoritmo de división es el siguiente:
Algoritmo: División
Entradas: enteros\(n\) y\(d\).
Variables locales:\(q\) y\(r\).
Vamos\(q = 0\).
Vamos\(r = n\).
Etiqueta\(1\).
Si\(r < d\) entonces
Regreso\(q\) y\(r\).
Finalizar Si
Vamos\(q = q + 1\).
Vamos\(r = r − d\).
Goto\(1\).
Este mismo algoritmo se da en forma de diagrama de flujo en la Figura\(1.5.2\).
Tenga en cuenta que en un diagrama de flujo la acción de una instrucción “Ir a” es clara porque una flecha apunta a la ubicación donde se está redirigiendo el flujo del programa. En pseudocódigo se requiere una instrucción “Label” que indica un punto donde el flujo puede ser redirigido a través de instrucciones posteriores “Goto”. Debido al potencial de confusión en algoritmos complicados que involucran multitudes de declaraciones Goto y sus correspondientes Labels, este tipo de redirección ahora está obsoleto en prácticamente todos los entornos de programación populares.
Antes de pasar a describir el algoritmo euclidiano, podría ser útil describir de manera más explícita para qué sirve exactamente. Dado un par de enteros,\(a\) y\(b\), hay dos cantidades que es importante para poder calcular, el mínimo común múltiplo o\(\text{lcm}\), y el mayor común divisor o\(\text{gcd}\). El\(\text{lcm}\) también va por el nombre mínimo común denominador porque es el denominador más pequeño que podría utilizarse como denominador común en el proceso de sumar dos fracciones que tenían\(a\) y\(b\) en sus denominadores. Los\(\text{gcd}\) y los\(\text{lcm}\) están relacionados por la fórmula
\[\text{lcm}(a,b) = \dfrac{ab}{\text{gcd}(a, b)} \]
por lo que son esencialmente equivalentes en cuanto a representar un desafío computacional.
El algoritmo euclidiano depende de una propiedad bastante extraordinaria del\(\text{gcd}\). Supongamos que estamos tratando de calcular\(\text{gcd}(a, b)\) y ese\(a\) es el mayor de los dos números. Primero alimentamos\(a\) y\(b\) en el algoritmo de división para encontrar\(q\) y\(r\) tal que\(a = qb + r\). Resulta que\(b\) y\(r\) tienen el mismo gcd que lo hicieron\(a\) y\(b\). En otras palabras\(\text{gcd}(a, b) = \text{gcd}(b, r)\), ¡además estos números son más pequeños que los que empezamos con! Esto es agradable porque significa que ahora estamos lidiando con una versión más fácil del mismo problema. Al diseñar un algoritmo es importante formular un criterio de finalización claro, una condición que te diga que has terminado. En el caso del algoritmo euclidiano, sabemos que terminamos cuando\(r\) sale el resto\(0\).
Entonces, aquí, sin más preámbulos está el algoritmo euclidiano en pseudocódigo.
Algoritmo: Euclides
Entradas: enteros\(a\) y\(b\).
Variables locales:\(q\) y\(r\).
Etiqueta\(1\).
Let\((q, r)\) = División\((a, b)\).
Si\(r = 0\) entonces
Regreso\(b\).
Finalizar Si
Vamos\(a = b\).
Vamos\(b = r\).
Goto\(1\).
Cabe señalar que para números pequeños uno puede encontrar el\(\text{gcd}\) y con\(\text{lcm}\) bastante facilidad al considerar sus factorizaciones en primos. Por el momento considera números que factorizan en primos pero no en poderes primos (es decir, sus factorizaciones no involucran exponentes). El\(\text{gcd}\) es el producto de los primos que están en común entre estas factorizaciones (si no hay primos en común lo es\(1\)). El\(\text{lcm}\) es producto de todos los primos distintos que aparecen en las factorizaciones. Como ejemplo, considere\(30\) y\(42\). Las factorizaciones son\(30 = 2 · 3 · 5\) y\(42 = 2 · 3 · 7\). Los primos que son comunes a ambas factorizaciones son\(2\) y\(3\), así\(\text{gcd}(30, 42) = 2 · 3 = 6\). El conjunto de todos los primos que aparecen en cualquiera de las factorizaciones es\(\{2, 3, 5, 7\}\) así\(\text{lcm}(30, 42) = 2 · 3 · 5 · 7 = 210\).
La técnica que se acaba de describir es de poco valor para números que tienen más de aproximadamente dígitos\(50\) decimales porque descansa a priori en la capacidad de encontrar las factorizaciones primos de los números involucrados. Factorizar números es bastante fácil si son razonablemente pequeños, especialmente si algunos de sus factores primos son pequeños, pero en general el problema se considera tan difícil que muchos esquemas criptográficos se basan en él.
Ejercicios
Trace a través del algoritmo de división con entradas\(n = 27\) y\(d = 5\), cada vez que se encuentre una sentencia de asignación, escríbala. ¿Cuántas asignaciones están involucradas en este cálculo en particular?
Encuentra los\(\text{gcd}\)\(\text{lcm}\)'s y los de los siguientes pares de números.
| \(a\) | \(b\) | \(\text{gcd}(a, b)\) | \(\text{lcm}(a, b)\) |
| 110 | 273 | ||
| 105 | 42 | ||
| 168 | 189 |
Formular una descripción del gcd de dos números en términos de sus factorizaciones primos en el caso general (cuando las factorizaciones puedan incluir poderes de los primos involucrados).
Traza a través del algoritmo euclidiano con entradas\(a = 3731\) y\(b = 2730\), cada vez que se encuentra la sentencia de asignación que llama al algoritmo de división escribe la expresión\(a = qb + r\). (¡Con los valores reales involucrados!)


