5.1: El principio de inducción matemática
- Page ID
- 114007
El Principio de Inducción Matemática (PMI) puede ser el método de prueba menos intuitivo disponible para nosotros. En efecto, al principio, el PMI puede sentirse algo parecido a agarrarse por el asiento de sus pantalones y levantarse en el aire. A pesar del hecho indiscutible de que las pruebas por PMI a menudo se sienten como mágicas, necesitamos convencerte de la validez de esta técnica de prueba. ¡Es una de las herramientas más importantes en tu kit matemático!
El argumento más simple a favor de la validez del PMI es simplemente que es axiomático. Esto puede parecer algo insatisfactorio, pero los axiomas para el sistema numérico natural, conocidos como los axiomas de Peano, incluyen uno que justifica el PMI. Los axiomas de Peano no serán tratados a fondo en este libro, pero aquí están:
- Hay un elemento mínimo de\(\mathbb{N}\) eso que denotamos por\(0\).
- Cada número natural a tiene un sucesor denotado por\(s(a)\). (Intuitivamente, piense en\(s(a) = a + 1\).)
- No hay un número natural cuyo sucesor sea\(0\). (En otras palabras,\(-1\) no está en\(\mathbb{N}\).)
- Los números naturales distintos tienen sucesores distintos. (\(a \neq b \implies s(a) \neq s(b)\))
- Si un subconjunto de los números naturales contiene\(0\) y también tiene la propiedad de que siempre\(a ∈ S\) que siga eso\(s(a) ∈ S\), entonces el subconjunto\(S\) es realmente igual a\(\mathbb{N}\).
El último axioma es el que justifica el PMI. Básicamente, si\(0\) está en un subconjunto, y el subconjunto tiene esta propiedad sobre los sucesores 1, entonces\(1\) debe estar en él. Pero si\(1\) está en él, entonces\(1\) el sucesor (\(2\)) debe estar en él. Y así sucesivamente..
El subconjunto termina teniendo cada número natural en él.
Verificar que la siguiente formulación simbólica tenga el mismo contenido que la versión del axioma\(5^{\text{th}}\) Peano dada anteriormente.
\(∀S ⊆ N (0 ∈ S) ∧ (∀a ∈ \mathbb{N}, a ∈ S \implies s(a) ∈ S) \implies S = \mathbb{N}\)
En agosto\(16^{\text{th}}\)\(2003\), Ma Lihua de Beijing, China, se ganó su lugar en los libros de discos al establecer sin ayuda un arreglo de dominó de punta (en realidad, la configuración tomó\(7\) semanas y casi fue arruinada por algunas cucarachas en el Singapore Expo Hall) y derribándolas. Después de que el primer dominó se volcó tardó unos seis minutos antes de que\(303,621\) fuera de las fichas de\(303,628\) dominó había caído. (Uno tiene que preguntarse qué mantuvo a esos otros\(7\) dominó erguidos.)
Este es el modelo que hay que tener en cuenta a la hora de pensar en PMI: el derribo de dominó. Al montar una línea de dominó, ¿qué debemos hacer para asegurarnos de que todos caigan cuando comience el derribo? Todo dominó debe colocarse para que golpee y derroque a su sucesor. Esto es exactamente análogo a\((a ∈ S \implies s(a) ∈ S)\). (Piense en\(S\) tener el criterio de membresía,\(x ∈ S =\) “\(x\)habrá caído cuando termine el derribo”). Lo otro que tiene que pasar (salvo la acción de las cucarachas) es que alguien golpee el primer dominó. Esto es análogo a\(0 ∈ S\).
En lugar de seguir hablando de subconjuntos de los naturales, será conveniente reformular nuestra discusión en términos de familias infinitas de afirmaciones lógicas. Si tenemos una secuencia de declaraciones, (una por cada número natural)\(P_0, P_1, P_2, P_3, . . .\) podemos demostrar que todas son ciertas usando PMI. Tenemos que hacer dos cosas. Primero —y esta suele ser la parte fácil— debemos demostrar que P0 es cierto (es decir, el primer dominó será derribado). Segundo, debemos mostrar, por cada valor posible de\(k\),\(P_k \implies P_{k+1}\) (es decir, cada dominó derribará a su sucesor). Estas dos partes de una prueba inductiva se conocen, respectivamente, como la base y el paso inductivo.
Un esquema para una prueba usando PMI:
\[∀n ∈ N, P_n\]
- Prueba
-
(Por inducción)
Bases:.. (Aquí debemos demostrar que\(P_0\) es cierto.)
Paso inductivo:.. (Aquí debemos demostrar que\(∀k, P_k \implies P_{k+1}\) es cierto.)
Q.E.D.
Pronto haremos un ejemplo real de una prueba inductiva, pero primero tenemos que decir algo REALMENTE IMPORTANTE sobre tales pruebas. ¡Presta atención! Esto es REALMENTE IMPORTANTE! Al hacer la segunda parte de una prueba inductiva (el paso inductivo), estás probando un SCP, y si recuerdas cómo se hace eso, empiezas asumiendo que el antecedente es cierto. Pero el UCS particular con el que vamos a tratar es\(∀k, P_k \implies P_{k+1}\). Eso quiere decir que en el transcurso de la prueba\(∀n\),\(P_n\) tenemos que asumir que eso\(P_k\) es cierto. Ahora bien, esto suena muy parecido al error conocido como “razonamiento circular”, sobre todo porque muchos autores ni siquiera usan letras diferentes (\(n\)versus\(k\) en nuestro esquema) para distinguir las dos afirmaciones. (Y, honestamente, solo introdujimos la variable\(k\) para apaciguar una cierta culpabilidad persistente con respecto al razonamiento circular). La sentencia\(∀n\),\(P_n\) es lo que estamos tratando de probar, pero la sentencia que necesitamos probar para poder hacer eso es\(∀k, P_k \implies P_{k+1}\). Esto es sutilmente diferente, al probarlo\(∀k\),\(P_k \implies P_{k+1}\) (¡que es un SCU!) asumimos que\(P_k\) es cierto para algún valor particular de\(k\).
La frase Pk se conoce como la hipótesis inductiva. Piénsalo de esta manera: Si estuviéramos haciendo una prueba completamente separada de\(∀n\)\(P_n \implies P_{n+1}\),, ciertamente sería justo usar la hipótesis inductiva, y una vez hecha esa prueba, estaría bien citar ese resultado en una prueba inductiva de\(∀n\),\(P_n\). ¡Así podemos compartimentalizar nuestra salida de la dificultad!
Bien, así sucesivamente a un ejemplo. En la Sección 4.1, descubrimos una fórmula que relaciona los tamaños de un conjunto\(A\) y su conjunto de potencia\(\mathcal{P}(A)\). Si\(|A| = n\) entonces\(|\mathcal{P}(A)| = 2^n\). Lo que tenemos aquí es una familia infinita de oraciones lógicas, una por cada valor de\(n\) en los números naturales,
\(|A| = 0 \implies |\mathcal{P}(A)| = 2^0, \\ |A| = 1 \implies |\mathcal{P}(A)| = 2^1, \\ |A| = 2 \implies |\mathcal{P}(A)| = 2^2, \\ |A| = 3 \implies |\mathcal{P}(A)| = 2^3,\)
etcétera.
Este es exactamente el tipo de situación en la que usamos la inducción
Para todos los conjuntos finitos\(A\),
\[|A| = n \implies |\mathcal{P}(A)| = 2^n.\]
- Prueba
-
Dejar\(n = |A|\) y proceder por inducción encendido\(n\).
Base: Supongamos que\(A\) es un conjunto finito y\(|A| = 0\), de ello se deduce que\(A = ∅\). El conjunto de potencia de\(∅\) es\(\{∅\}\) que es un conjunto que tiene\(1\) elemento. Tenga en cuenta que\(2^0 = 1\).
Paso inductivo: Supongamos que\(A\) es un conjunto finito con\(|A| = k + 1\). Elija algún elemento particular de\(A\), digamos\(a\), y tenga en cuenta que podemos dividir los subconjuntos de\(A\) (es decir, elementos de\(\mathcal{P}(A)\)) en dos categorías, las que contienen\(a\) y las que no.
Dejar\(S_1 = \{X ∈ \mathcal{P}(A) a ∈ X\}\) y dejar\(S_2 = \{X ∈ \mathcal{P}(A) a \notin X\}\). Hemos creado dos conjuntos que contienen todos los elementos de\(\mathcal{P}(A)\), y que son disjuntos entre sí. En forma simbólica,\(S_1 ∪ S_2 = \mathcal{P}(A)\) y\(S_1 ∩ S_2 = ∅\). De ello se deduce que\(|\mathcal{P}(A)| = |S_1| + |S_2|\).
Observe que en realidad\(S_2\) es el conjunto de potencia del conjunto\(k\) -element\(A \setminus \{a\}\). Por la hipótesis inductiva,\(|S_2| = 2^k\). Además, observe que cada conjunto en\(S_1\) corresponde de manera única a un conjunto en\(S_2\) si simplemente eliminamos el elemento a de él. Esto demuestra que\(|S_1| = |S_2|\). Armando todo esto lo conseguimos\(|P(A)| = 2^k + 2^k = 2(2^k) = 2^{k+1}\).
Q.E.D.
Aquí hay algunos consejos sobre pruebas por inducción:
- Declaraciones que se pueden probar inductivamente no siempre empiezan con\(P_0\). A veces\(P_1\) es la primera declaración en una familia infinita. A veces lo es\(P_5\). No te molestes por algo que podría manejarse renumerando las cosas.
- En tu redacción final solo necesitas probar el caso inicial (cualquiera que sea) para la base, pero es una buena idea probar los primeros casos mientras estás en la etapa de “draft”. Esto puede proporcionar información sobre cómo probar el paso inductivo, y también puede ayudarlo a evitar un error clásico en el que el enfoque inductivo falla esencialmente solo porque hay una brecha entre dos de los dominó anteriores. 2
- Es una buena idea anotar en algún lugar justo lo que es lo que necesita ser probado en el paso inductivo, simplemente no hagas que parezca que estás asumiendo lo que hay que mostrar. Por ejemplo, en la prueba anterior podría haber sido agradable comenzar el paso inductivo con un comentario en las siguientes líneas, “Lo que necesitamos mostrar es que bajo el supuesto de que cualquier conjunto de tamaño\(k\) tiene un conjunto de potencia de tamaño\(2^k\), se deduce que un conjunto de tamaño\(k + 1\) tendrá un conjunto de potencia de tamaño\(2^{k+1}\).”
Cerraremos esta sección con una breve discusión sobre nada.
Cuando introdujimos por primera vez los números naturales (\(\mathbb{N}\)) en el Capítulo 1 decidimos seguir la convención de que el número natural más pequeño es\(1\). Habrás notado que los axiomas de Peano mencionados al inicio de esta sección tratan\(0\) como el número natural más pequeño. Entonces, de aquí en adelante vamos a cambiar las cosas de un lado con el doctor Peano. Es decir, a partir de ahora usaremos la convención
\(\mathbb{N} = \{0, 1, 2, 3, . . .\}\)
Hmmm. A lo mejor fue una breve discusión sobre algo después de todo.
Ejercicios:
Considera la secuencia de números que son\(1\) mayores que un múltiplo de\(4\). (Tales números son de la forma\(4j + 1\).)
\(1, 5, 9, 13, 17, 21, 25, 29, . . .\)
La suma de los primeros números de esta secuencia se puede expresar como un polinomio.
\(\sum^{n}_{j=0} 4j + 1 = 2n^2 + 3n + 1\)
Complete la siguiente tabla con el fin de aportar evidencia de que la fórmula anterior es correcta.
| \(n\) | \(\sum^{n}_{j=0} 4j + 1\) | \(2n^2 + 3n + 1\) |
|---|---|---|
| \ (n\) ">\(0\) | \ (\ suma^ {n} _ {j=0} 4j + 1\) ">\(1\) | \ (2n^2 + 3n + 1\) ">\(1\) |
| \ (n\) ">\(1\) | \ (\ suma^ {n} _ {j=0} 4j + 1\) ">\(1 + 5\) | \ (2n^2 + 3n + 1\) ">\(2 · 1^2 + 3 · 1 + 1 = 6\) |
| \ (n\) ">\(2\) | \ (\ suma^ {n} _ {j=0} 4j + 1\) ">\(1 + 5 + 9 =\) | \ (2n^2 + 3n + 1\) "> |
| \ (n\) ">\(3\) | \ (\ suma^ {n} _ {j=0} 4j + 1\) "> | \ (2n^2 + 3n + 1\) "> |
| \ (n\) ">\(4\) | \ (\ suma^ {n} _ {j=0} 4j + 1\) "> | \ (2n^2 + 3n + 1\) "> |
¿Qué tiene de malo la siguiente prueba inductiva de que “todos los caballos son del mismo color”.?
\(H\)Sea un juego de\(n\) caballos, todos los caballos en\(H\) son del mismo color.
Prueba: Procedemos por inducción en\(n\).
Base: Supongamos que\(H\) es un conjunto que contiene\(1\) caballo. Claramente, este caballo es del mismo color que él mismo.
Paso inductivo: Dado un juego de\(k + 1\) caballos\(H\) podemos construir dos juegos de\(k\) caballos. Supongamos\(H = \{h_1, h_2, h_3, . . . h_{k+1}\}\). Definir\(H_a = \{h_1, h_2, h_3, . . . h_k\}\) (es decir,\(H_a\) contiene solo los primeros\(k\) caballos) y\(H_b = \{h_2, h_3, h_4, . . . h_{k+1}\}\) (es decir,\(H_b\) contiene los últimos\(k\) caballos). Por la hipótesis inductiva ambos conjuntos contienen caballos que son “todos del mismo color”. También, todos los caballos de\(h_2\) a\(h_k\) están en ambos conjuntos así que ambos\(H_a\) y\(H_b\) contienen sólo caballos de este (mismo) color. Finalmente, concluimos que todos los caballos en\(H\) son del mismo color.
Q.E.D.
Para cada uno de los siguientes teoremas, escribe el enunciado que debe probarse para la base — ¡entonces demuéstralo, si puedes!
La suma de los primeros enteros\(n\) positivos es\(\dfrac{(n^2 + n)}{2}\).
La suma de los primeros números impares\(n\) (positivos) es\(n^2\).
Si se voltean\(n\) monedas, la probabilidad de que todas sean “cabezas” es\(\dfrac{1}{2}^n\).
Cada\(2^n × 2^n\) tablero de ajedrez, con un cuadrado quitado, se puede alicatar perfectamente 3 por trominos en forma de L. (Un trominoe es como un dominó pero conformado por\(3\) cuadraditos. Hay dos tipos, recto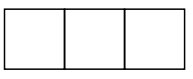
y en forma de
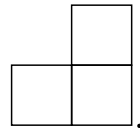L. Este problema sólo se refiere a los trominos en forma de L.)
Supongamos que las reglas del juego para PMI fueron cambiadas para que uno hiciera lo siguiente:
- Bases: Demostrar que\(P(0)\) es verdad.
- Paso inductivo: Demostrar que para todos\(k\),\(P_k\) implica\(P_{k+2}\)
Explique por qué esto no constituiría una prueba válida que se\(P_n\) mantenga para todos los números naturales\(n\). ¿Cómo podríamos cambiar la base en este esquema para obtener una prueba válida?
Si quisiéramos probar declaraciones que estaban indexadas por los enteros,
\(∀z ∈ \mathbb{Z}\),\(P_z\),
¿qué cambios se deben hacer al PMI?