6.2: Propiedades de las Relaciones
- Page ID
- 114091
Hay dos clases especiales de relaciones que estudiaremos en las dos secciones siguientes, las relaciones de equivalencia y las relaciones de orden. El prototipo para una relación de equivalencia es la noción ordinaria de igualdad numérica,\(=\). La relación prototípica de ordenación es\(≤\). Cada uno de estos tiene ciertas propiedades sobresalientes que son las causas fundamentales de su importancia. En esta sección, estudiaremos un compendio de propiedades que una relación puede o no tener.
Una relación que tiene tres de las propiedades que discutiremos:
- reflexividad
- simetría
- transitividad
se dice que es una relación de equivalencia; de alguna manera se asemejará\(=\).
Una relación que tiene otro conjunto de tres propiedades:
- reflexividad
- anti-simetría
- transitividad
se llama relación de orden; se asemejará\(≤\).
Adicionalmente, existe una propiedad conocida como irreflexividad que muchas relaciones tienen.
Hay un total de\(5\) propiedades que hemos nombrado, y las discutiremos más a fondo. Pero primero, vamos a exponer las definiciones formales. Toma nota que todas estas propiedades están declaradas para una relación que va de un conjunto a sí mismo, de hecho, la mayoría de ellas ni siquiera tendrían sentido si tratáramos de definirlas para una relación de un conjunto a otro conjunto diferente.
| Cuadro 6.2.1: Propiedades que las Relaciones pueden (o no) tener. |
|---|
|
Una relación\(\text{R}\) en un conjunto\(S\) es reflexiva iff \(∀a ∈ S, \;\;\;\; a \text{R}a\) “Todo está relacionado consigo mismo”. |
|
Una relación\(\text{R}\) en un conjunto\(S\) es irreflexiva iff \(∀a ∈ S, \;\;\;\; a\not \text{R} a\) “Nada está relacionado consigo mismo”. |
|
Una relación\(\text{R}\) en un conjunto\(S\) es simétrica iff \(∀a, b ∈ S, \;\;\;\; a\text{R}b \implies b\text{R}a\) “No hay calles de un solo sentido”. |
|
Una relación\(\text{R}\) en un conjunto\(S\) es antisimétrica iff \(∀a, b ∈ S, \;\;\;\; a\text{R}b ∧ b\text{R}a \implies a = b\) “Sólo calles de un solo sentido”. |
|
Una relación\(\text{R}\) en un conjunto\(S\) es transitiva iff \(∀a, b, c ∈ S, \;\;\;\; a\text{R}b ∧ b\text{R}c \implies a\text{R}c\) “Siempre que hay una ruta de rotonda, hay una ruta directa”. |
El dígrafo de una relación reflexiva tendrá pequeños bucles en cada vértice. El dígrafo de una relación irreflexiva no contendrá ningún bucle. Ojalá quede claro que estos conceptos representan posibilidades extremas opuestas —sin embargo, no son negaciones entre sí.
Encuentra la negación lógica de la propiedad que dice que una relación es reflexiva
\(¬(∀a ∈ S, \;\;\;\; a\text{R}a)\).
¿En qué se diferencia esto de la propiedad definitoria para “irreflexiva”?
Si\(\text{R}\) se define una relación en algún subconjunto\(S\) de los reales, entonces se puede graficar en el plano euclidiano. La reflexividad para se\(\text{R}\) puede interpretar en términos de la línea\(L\) definida por la ecuación\(y = x\). Cada punto en\((S × S)∩L\) debe estar adentro\(\text{R}\). Se puede hacer una declaración similar con respecto a la propiedad irreflexiva. Si una relación\(\text{R}\) es irreflexiva su gráfica evita completamente la línea\(y = x\).
Tenga en cuenta que las propiedades reflexivas e irreflexivas se definen con una sola variable cuantificada. La simetría y la antisimetría requieren dos variables cuantificadas universalmente para sus definiciones.
Una relación\(\text{R}\) en un conjunto\(S\) es simétrica iff
\[∀a, b ∈ S, \;\;\;\; a\text{R}b \implies b\text{R}a.\]
Esto se puede interpretar en términos de dígrafos de la siguiente manera: Si\(b\) existe una conexión de\(a\) a en el dígrafo de\(\text{R}\), entonces también debe haber una conexión de\(b\) a\(a\). En Tabla\(6.2.1\) esto se interpreta como “sin calles unidireccionales” y si bien eso no es exactamente lo que dice, ese es el efecto de esta definición. Ya que si existe una conexión en una dirección, también debe haber una conexión en la otra dirección, se deduce que nunca veremos una conexión unidireccional.
Debido a que la mayoría de las propiedades que estamos estudiando se definen usando declaraciones condicionales suele darse el caso de que una relación tenga una propiedad por razones vacuas. Cuando la parte “si” no sucede, tampoco hay necesidad de que suceda su correspondiente parte de “entonces” —el condicional sigue siendo cierto. En el contexto de nuestra discusión sobre la propiedad de simetría de una relación, esto significa que el siguiente dígrafo es el dígrafo de una relación simétrica (aunque no es ni reflexiva ni irreflexiva).
La antisimetría se describe con el significado de “solo calles unidireccionales” pero la definición se da como:
Una relación\(\text{R}\) en un conjunto\(S\) es antisimétrica iff
\[∀a, b ∈ S, \;\;\;\; a\text{R}b ∧ b\text{R}a \implies a = b.\]
Puede ser difícil al principio entender por qué la definición que usamos para la antisimetría es la anterior. Si uno quisiera asegurar que nunca hubo conexiones bidireccionales entre los elementos del conjunto, podría parecer más fácil definir la antisimetría de la siguiente manera:
(Definición alternativa) Una relación\(\text{R}\) en un conjunto\(S\) es antisimétrica iff
\[∀a, b ∈ S, \;\;\;\; a\text{R}b \implies b \not Ra.\]
Esta definición puede parecer más sencilla, pero resulta que la definición original es más fácil de usar en pruebas. Tenemos que convencernos de que la (primera) definición realmente logra lo que queremos. Es decir, si una relación\(\text{R}\) satisface la propiedad que\(∀a, b ∈ S, \;\;\;\; a\text{R}b ∧ b\text{R}a \implies a = b\), entonces en realidad no habrá ningún par de elementos que estén relacionados en ambos órdenes. Una manera de pensarlo es esta: supongamos que\(a\) y\(b\) son elementos distintos de\(S\) y que ambos\(a\text{R}b\) y\(b\text{R}a\) son verdaderos. El inmueble garantiza ahora aquello\(a = b\) que contradice la noción de que\(a\) y\(b\) son distintos. Esta es una prueba en miniatura por contradicción; si asumes que hay un par de elementos distintos que están relacionados en ambos órdenes obtienes una contradicción, ¡entonces no los hay!
Algo curioso de la propiedad antisimetría es esto: Cuando es cierto de una relación, ¡siempre es vacuamente cierto! El inmueble está diseñado de tal manera que cuando es cierto, obliga a que la afirmación en su antecedente nunca suceda realmente.
La transitividad es una propiedad sumamente útil como atestigua el hecho de que tanto las relaciones de equivalencia como las relaciones de orden deben tener esta propiedad. Al hablar de la propiedad transitiva de la igualdad decimos “Dos cosas que son iguales a una tercera, son iguales entre sí”. Al tratar de ordenar podemos encontrar declaraciones como las siguientes. “Dado que 'Aardvark' precede a 'Baluarte' en el diccionario, y dado que 'Baluarte' precede a 'Catástrofe', es claro que 'Aardvark' viene antes de 'Catástrofe' en el diccionario”.
Nuevamente, la definición de transitividad implica un condicional. Además, la transitividad puede ser vista como la más complicada de las propiedades que hemos estado estudiando; se necesitan tres variables universalmente cuantificadas para declarar la propiedad.
Una relación\(\text{R}\) en un conjunto\(S\) es transitiva iff
\[∀a, b, c ∈ S, \;\;\;\; a\text{R}b ∧ b\text{R}c \implies a\text{R}c\]
Parafraseamos la transitividad como “Siempre que hay una ruta de rotonda, hay una ruta directa”. En particular, lo que dice la definición es que si hay una conexión desde\(b\) y\(a\)\(b\) hacia\(c\) (la ruta de rotonda de\(a\) a\(c\)) entonces debe haber una conexión de\(a\) a\(c\) (la ruta directa).
Realmente necesitarás estar atento a las relaciones que son transitivas por razones vacuas. Siempre y cuando uno nunca tenga tres elementos\(a\),\(b\) y\(c\) con\(a\text{R}b\) y\(b\text{R}c\) la afirmación que define la transitividad es automáticamente cierta.
Una manera muy útil de pensar sobre estas diversas propiedades que pueden tener las relaciones es en términos de lo que no sucede cuando una relación las tiene. Antes de continuar, es importante que hagas lo siguiente
Encuentra negaciones lógicas para las propiedades formales que definen cada una de las cinco propiedades.
Si una relación\(\text{R}\) es reflexiva nunca veremos un nodo que no tenga bucle.
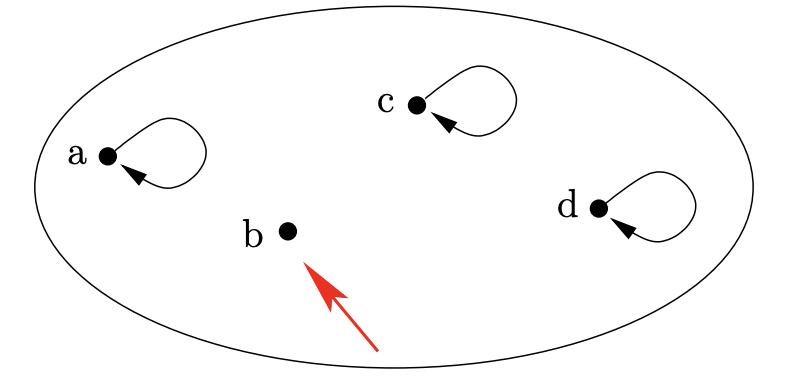
¡Si una relación\(\text{R}\) es irreflexiva nunca veremos un nodo que sí tenga un bucle!
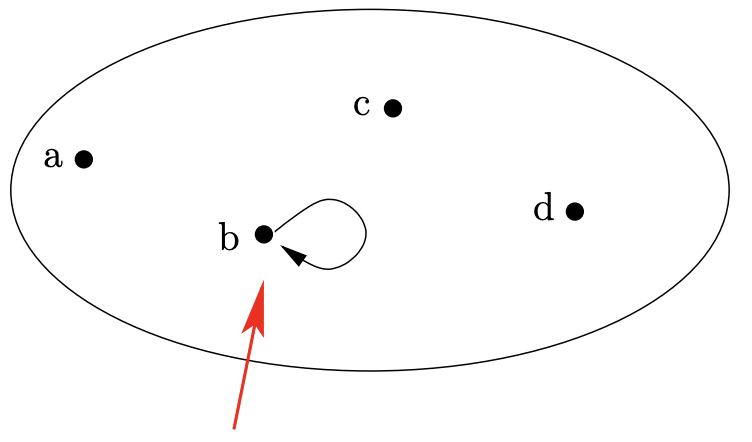
Si una relación\(\text{R}\) es simétrica nunca veremos un par de nodos que estén conectados en una sola dirección.
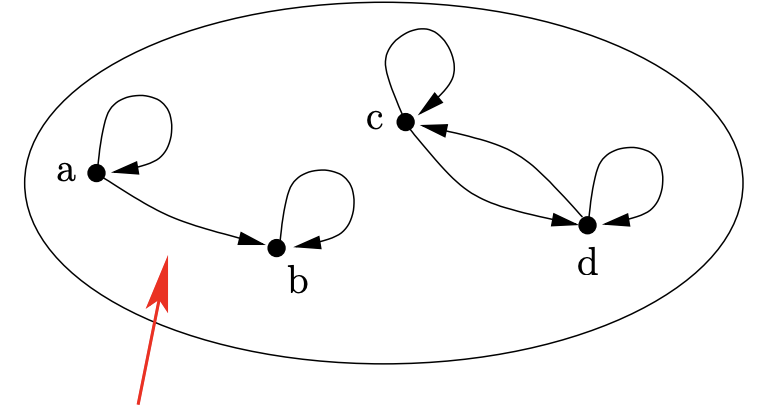
Si una relación\(\text{R}\) es antisimétrica nunca veremos un par de nodos que estén conectados en ambas direcciones.
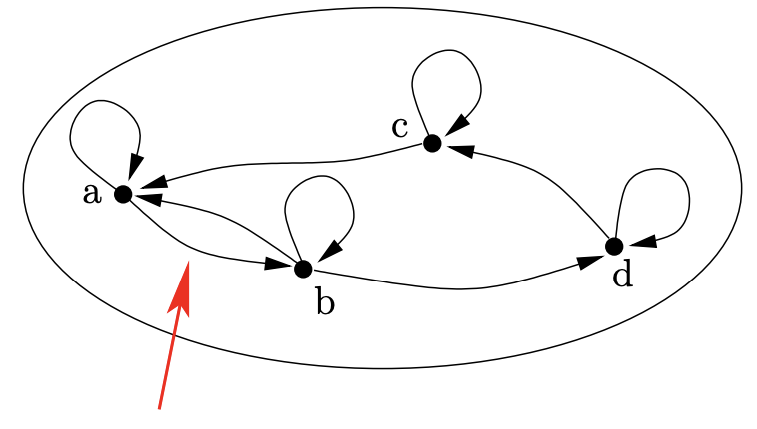
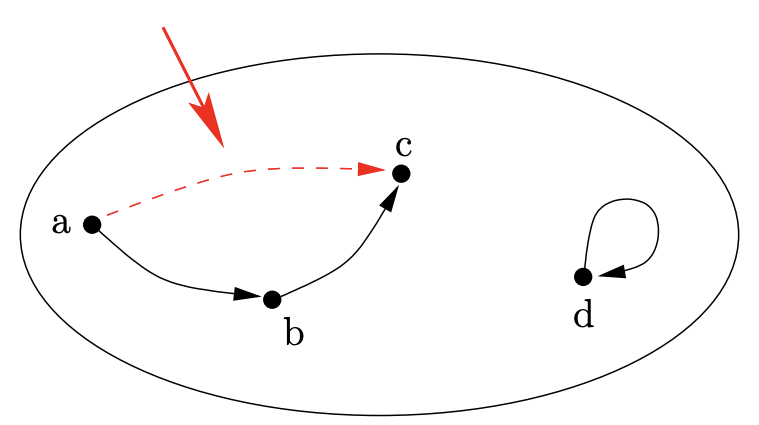
Si una relación\(\text{R}\) es transitiva lo que nunca veremos es un poco más difícil de describir. Nunca habrá un par de flechas encontrándose cabeza a cola sin que haya también una flecha que vaya de la cola de la primera a la cabeza de la segunda.
Ejercicios:
Considerar la relación\(\text{S}\) definida por\(\text{S} = \{(x, y) x \text{ is smarter than } y\}\). ¿Es\(\text{S}\) simétrico o antisimétrico? Explique.
Considerar la relación\(\text{A}\) definida por\(\text{A} = \{(x, y) x \text{ has the same astrological sign as } y\}\). ¿Es\(\text{A}\) simétrico o antisimétrico? Explique.
Explique por qué ambas relaciones que acabamos de describir (en los problemas 1 y 2) tienen la propiedad transitiva.
Para cada una de las cinco propiedades, nombra una relación que la tenga y una relación que no.
Mostrar por contraejemplo que “\(|\)” (divisibilidad) no es simétrico como una relación sobre\(\mathbb{Z}\).
Demostrar que “\(|\)” es una relación ordenadora (hay que verificar que es reflexiva, antisimétrica y transitiva).


