6.3: Relaciones de equivalencia
- Page ID
- 114100
La idea principal de una relación de equivalencia es que es algo así como la igualdad, pero no del todo. Por lo general hay alguna propiedad que podamos nombrar, por lo que esas cosas equivalentes comparten esa propiedad. Por ejemplo Albert Einstein y Adolf Eichmann eran dos seres humanos completamente diferentes, si consideras todos los diferentes criterios que se pueden utilizar para distinguir a los seres humanos hay poco que tienen en común. Pero, si lo único que le interesaba a uno eran las iniciales de una persona, habría que decir que Einstein y Eichmann eran equivalentes. Futuros ejemplos de relaciones de equivalencia serán menos frívolos. Pero primero, la definición formal:
Una relación\(\text{R}\) sobre un conjunto\(S\) es una relación de equivalencia si\(\text{R}\) es reflexiva, simétrica y transitiva.
Probablemente la relación de equivalencia más importante que hemos visto hasta la fecha es “congruencia\(\text{mod } m\)” que denotaremos usando el símbolo\(≡_m\). ¡Esta relación puede ser incluso más interesante que la igualdad real! La razón de esta afirmación aparentemente extraña es que la “congruencia\(\text{mod } m\)” nos da clases de equivalencia no triviales. Las clases de equivalencia son una de las ideas más potentes de las matemáticas modernas y es esencial que las entiendas, así que comenzaremos con un ejemplo. Considera la congruencia\(\text{mod } 5\). ¿A qué otros números es (digamos)\(11\) equivalente? ¡Hay muchos! Cualquier número que deje el mismo resto que\(11\) cuando lo dividimos por\(5\). Esta colección se llama la clase de equivalencia de\(11\) y generalmente se denota usando un overline\(\overline{11}\), otra notación que a menudo se ve para el conjunto de cosas equivalentes a\(11\) is\(11/ ≡_5\).
\(\overline{11} = \{. . . , −9, −4, 1, 6, 11, 16, . . .\}\)
Es fácil ver que obtendremos exactamente el mismo conjunto si elegimos cualquier otro elemento de la clase de equivalencia (en lugar de\(11\)), lo que nos lleva a una lista infinita de igualdades de conjunto,
\(\overline{1} = \overline{6} = \overline{11} = . . .\)
Y de manera similar,
\(\overline{2} = \overline{7} = \overline{12} = . . .\)
De hecho, en realidad solo hay\(5\) diferentes conjuntos que forman las clases de equivalencia\(\text{mod } 5\):\(\overline{0}\)\(\overline{1}\),\(\overline{2}\),\(\overline{3}\), y\(\overline{4}\). (Nota: hemos seguido la convención habitual de usar los números enteros no negativos más pequeños posibles como representantes para nuestras clases de equivalencia.)
Lo que hemos estado discutiendo aquí es uno de los primeros ejemplos de una estructura de cociente. Comenzamos con los enteros y “mod out” por una relación de equivalencia. Al hacerlo, “pasamos al cociente” lo que significa (en esta instancia) que pasamos de\(\mathbb{Z}\) a un conjunto mucho más simple que tiene solo cinco elementos:\(\{0, 1, 2, 3, 4\}\). Al pasar al cociente generalmente perderemos mucha información, pero destacaremos en gran medida alguna característica particular —en este ejemplo, propiedades relacionadas con la divisibilidad por\(5\).
Dada alguna relación de equivalencia\(\text{R}\) definida en un conjunto se denota\(S\) el conjunto de clases de equivalencia de\(S\) under\(\text{R}\)\(S/\text{R}\) (que se lee “\(S \text{ mod } \text{R}\)”). Este uso de la barra, normalmente reservada para la división, no debería causar ninguna confusión ya que esos no son números a ambos lados de la barra, sino más bien un conjunto y una relación. Esta notación también puede aclarar por qué algunas personas denotan las clases de equivalencia anteriores por\(0/ ≡_5\),\(1/ ≡_5\),\(2/ ≡_5\),\(3/ ≡_5\) y\(4/ ≡_5\).
El conjunto de clases de equivalencia forma una partición del conjunto\(S\).
Una partición\(P\) de un conjunto\(S\) es un conjunto de conjuntos tal que
\[S = \bigcup_{X∈P} X \;\;\; \text{ and } \;\;\; ∀X, Y ∈ P, X \neq Y \implies X ∩ Y = ∅.\]
En palabras, si tomas la unión de todas las piezas de la partición obtendrás el conjunto\(S\), y cualquier par de conjuntos de la partición que no sean idénticos son disjuntos. Las particiones son una forma inherentemente útil de ver las cosas, aunque en el mundo real muchas veces hay problemas (los conjuntos que pensábamos que eran disjuntos resultan tener elementos en común, o descubrimos algo que no encaja en ninguna de las piezas de nuestra partición), en matemáticas, solemos encontrar que las particiones hacer justo lo que quisiéramos que hicieran. Las particiones dividen algunas configuraciones en una serie de piezas convenientes de tal manera que se nos garantiza que cada elemento del conjunto está en una de las piezas y también para que ninguna de las piezas se superponga. Las particiones son una forma útil de diseccionar conjuntos, y las relaciones de equivalencia (a través de sus clases de equivalencia) nos dan una manera fácil de crear particiones, ¡generalmente con alguna estructura adicional para arrancar! Las propiedades que hacen de una relación una relación de equivalencia (reflexividad, simetría y transitividad) están diseñadas para asegurar que existen clases de equivalencia y nos proporcionan la partición deseada. Para el escritor de prueba inicial todo esto puede parecer muy complicado, pero ¡anímate! La mayor parte del trabajo ya lo han hecho por ustedes quienes crearon la teoría general de las relaciones de equivalencia y las estructuras de cocientes. Todo lo que tienes que hacer (generalmente) es probar que una relación dada es una relación de equivalencia verificando que efectivamente es reflexiva, simétrica y transitiva. Echemos un vistazo a otro ejemplo.
En Teoría de Números, la parte libre de cuadrados de un entero es lo que queda después de dividir el cuadrado perfecto más grande que lo divide. (Esto también se conoce como el radical de un entero.) En la siguiente tabla se da la parte libre de cuadrados\(sf(n)\),, para los primeros varios valores de\(n\).
| \(n\) | \(1\; 2\; 3\; 4\; 5\; 6 \;7\; 8\; 9 \;10 \;11 \;12\; 13\; 14\; 15 \;16 \;17 \;18\; 19 \;20\) | |||
| \(sf(n)\) | \(1 \;2\; 3 \;1 \;5 \;6 \;7 \;2 \;1 \;10 \;11 \;3 \;13\; 14 \;15 \;1 \;17 \;2 \;19\; 5\) | |||
Es fácil calcular la parte libre de cuadrados de un entero si conoces su factorización principal, solo reduce todos los exponentes\(\text{mod } 2\). Por ejemplo 1
\(808017424794512875886459904961710757005754368000000000 = 246 · 3 20 · 5 9 · 7 6 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71\)
la parte libre de cuadrados de este número es
\(5 · 13 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71 = 3504253225343845\)
que, si bien sigue siendo un número bastante grande, ¡sin duda es un poco más pequeño que el original!
Definiremos una relación de equivalencia\(\text{S}\) en el conjunto de números naturales usando la parte libre de cuadrados:
\(∀x, y ∈ \mathbb{N}, x\text{S}y \iff sf(x) = sf(y)\)
Es decir, dos números naturales estarán\(\text{S}\) relacionados si tienen las mismas partes libres de cuadrados.
¿Qué es\(1/\text{S}\)?
Antes de proceder a la prueba de que\(\text{S}\) es una relación de equivalencia nos gustaría que conocieras un panorama más amplio a medida que lees. Cada una de las tres partes de la prueba tendrá una estructura similar. Mostraremos que\(\text{S}\) tiene una de las tres propiedades utilizando el hecho de que\(=\) tiene esa propiedad. En un trabajo más avanzado toda esta prueba podría omitirse o sustituirse por la frase “\(\text{S}\)hereda de la igualdad la reflexividad, la simetría y la transitividad, y por lo tanto es una relación de equivalencia”. (Buen truco, ¿no? Pero antes de que te permitan usarlo tienes que demostrar que puedes hacerlo de la manera más dura.).
La relación\(\text{S}\) definida por
\[∀x, y ∈ \mathbb{N}, x\text{S}y \iff sf(x) = sf(y)\]
es una relación de equivalencia sobre\(\mathbb{N}\).
- Prueba
-
Debemos demostrar que\(\text{S}\) es reflexivo, simétrico y transitivo.
reflexivo — (Aquí hay que demostrar eso\(∀x ∈ \mathbb{N}, x\text{S}x\).) Dejar\(x\) ser un número natural arbitrario. Ya que\(sf(x) = sf(x)\) (esta es la propiedad reflexiva de\(=\)) se desprende de la definición de\(\text{S}\) eso\(x\text{S}x\).
simétrico — (Aquí debemos demostrarlo\(∀x, y ∈ \mathbb{N}, x\text{S}y \implies y\text{S}x\).) Dejemos\(x\) y\(y\) sean números naturales arbitrarios, y supongamos además eso\(x\text{S}y\). Ya que\(x\text{S}y\), se desprende de la definición de\(\text{S}\) eso\(sf(x) = sf(y)\), obviamente entonces\(sf(y) = sf(x)\) (esta es la propiedad simétrica de\(=\)) y así\(y\text{S}x\).
transitivo — (Aquí debemos demostrarlo\(∀x, y, z ∈ \mathbb{N}, x\text{S}y ∧ y\text{S}z \implies x\text{S}z\).) Dejar\(x\),\(y\) y\(z\) ser arbitrarios números naturales, y además supongamos que tanto\(x\text{S}y\) y\(y\text{S}z\). De la definición de\(\text{S}\) deducimos eso\(sf(x) = sf(y)\) y\(sf(y) = sf(z)\). Claramente,\(sf(x) = sf(z)\) (esta deducción viene de la propiedad transitiva de\(=\)), entonces\(x\text{S}z\).
Q.E.D.
Terminaremos esta sección con un ejemplo de una relación de equivalencia que no “hereda” las tres propiedades de la igualdad.
Una gráfica es una estructura matemática que consta de dos conjuntos, un conjunto\(V\) de puntos (también conocido como vértices) y un conjunto 2\(E\) de aristas. Los elementos de\(E\) pueden ser pares ordenados o desordenados de\(V\). Si\(E\) consiste en pares ordenados tenemos una gráfica o dígrafo dirigido — ¡los diagramas que hemos estado usando para visualizar las relaciones! Si\(E\) consiste en pares desordenados entonces estamos tratando con una gráfica no dirigida. Dado que el caso no dirigido es en realidad el más habitual, si la palabra “graph” aparece sin un modificador se supone que estamos hablando de una gráfica no dirigida.
El párrafo anterior da una definición relativamente precisa de una gráfica en términos de conjuntos, sin embargo la manera real de pensar en las gráficas es en términos de diagramas donde un conjunto de puntos están conectados por caminos. (Los caminos, por supuesto, necesitarán tener flechas sobre ellos en dígrafos). A continuación se presentan algunos ejemplos de los diagramas que se utilizan para representar gráficas.
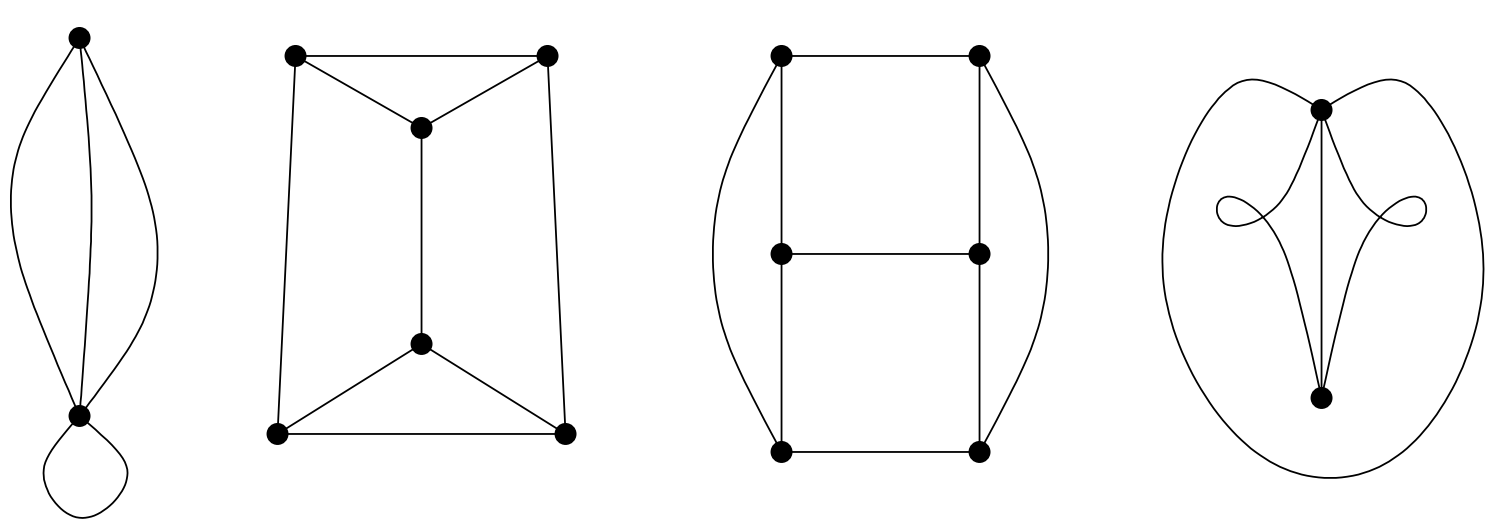
Se dice que dos gráficas son isomórficas si representan las mismas conexiones. En primer lugar debe haber una correspondencia uno a uno entre los vértices de las dos gráficas, y además, un par de vértices en una gráfica están conectados por algún número de aristas si y sólo si los vértices correspondientes en la otra gráfica están conectados por el mismo número de aristas.
Los cuatro ejemplos de gráficos anteriores en realidad son dos pares de gráficas isomórficas. ¿Qué pares son isomórficos?
Esta palabra “isomórfica” tiene una bonita etimología. Significa “misma forma”. Dos gráficas son isomórficas si tienen la misma forma. No tenemos las herramientas en este momento para hacer una prueba formal (de hecho necesitamos mirar algunos requisitos previos adicionales antes de poder definir realmente con precisión el isomorfismo), pero el isomorfismo de las gráficas es una relación de equivalencia. Al menos verifiquemos esto de manera informal.
Reflexivity: ¿Es una gráfica isomórfica consigo misma? Es decir, ¿una gráfica tiene la “misma forma” que ella misma? ¡Claramente!
Simetría: Si la gráfica\(A\) es isomórfica para graficar\(B\), ¿también es el caso de que la gráfica\(B\) sea isomórfica para graficar\(A\)? Es decir, si\(A\) tiene la “misma forma” que\(B\), ¿no\(B\) tiene la misma forma que\(A\)? ¡Por supuesto!
Transitividad: Bien.. la respuesta aquí va a ser “¡Naturalmente!” pero esperemos a profundizar en este tema cuando tengamos una definición formal utilizable para isomorfismo gráfico. Sin embargo, la pregunta en esta etapa debería ser clara: Si\(A\) es isomorfa a\(B\) y\(B\) es isomorfa a\(C\), entonces no es\(A\) isomorfa a\(C\)?
Ejercicios:
Considerar la relación\(\text{A}\) definida por
\(\text{A} = \{(x, y) x \text{ has the same astrological sign as } y\}\).
Demostrar que\(\text{A}\) es una relación de equivalencia. ¿A\(\text{A}\) qué clase de equivalencia perteneces?
Definir una relación\(\square\) sobre los enteros por\(x\square y \iff x^2 = y^2\). Demostrar que\(\square\) es una relación de equivalencia. Enumere las clases de equivalencia\(x/ \square\) para\(0 ≤ x ≤ 5\).
Definir una relación\(\text{A}\) en el conjunto de todas las palabras por
\(w_1\text{A}w_2 \iff w_1 \text{ is an anagram of } w_2\).
Demostrar que\(\text{A}\) es una relación de equivalencia. (Las palabras son anagramas si las letras de uno se pueden reorganizar para formar la otra. Por ejemplo, 'ART' y 'RAT' son anagramas.)
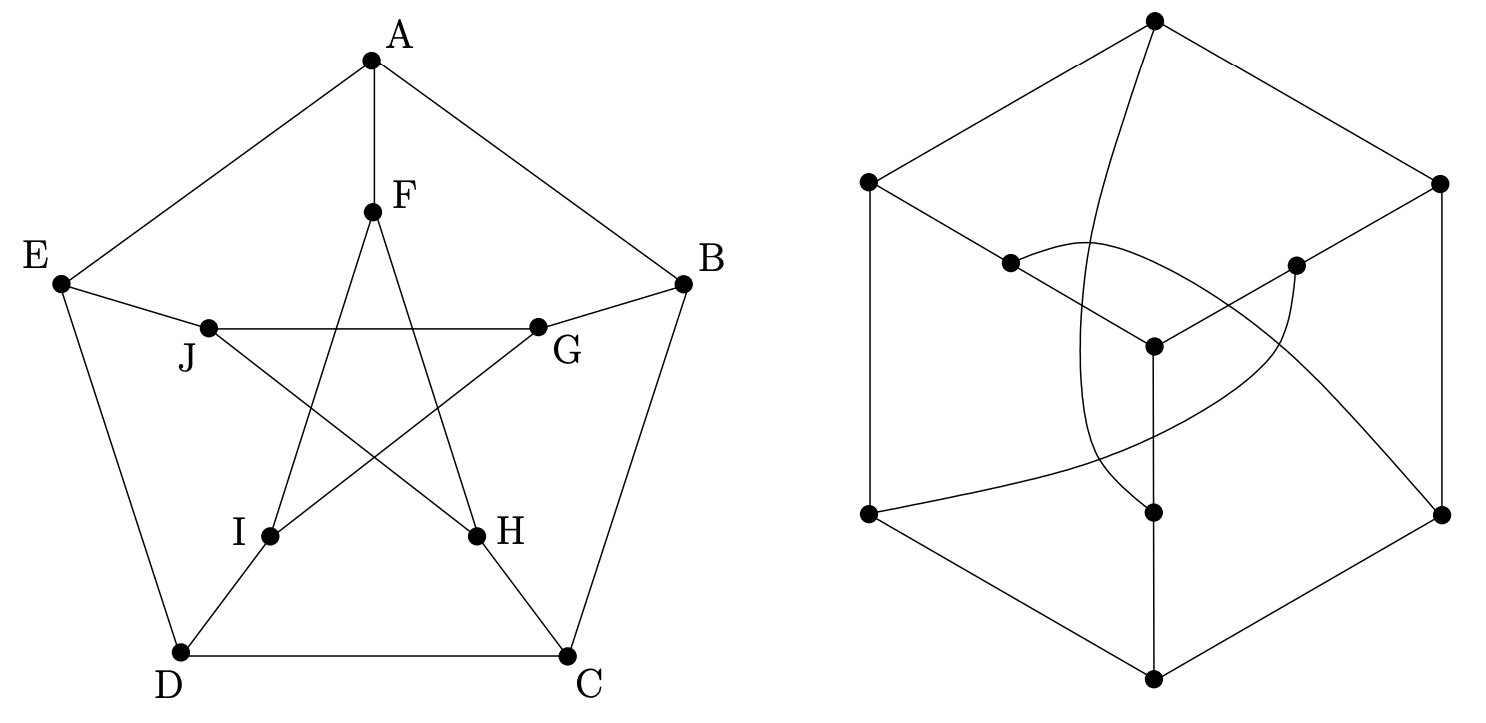
Los dos diagramas a continuación muestran ambos una famosa gráfica conocida como la gráfica Petersen. El cuadro de la izquierda es la representación habitual que enfatiza su simetría de cinco veces. El cuadro de la derecha resalta el hecho de que la gráfica de Petersen también tiene una simetría triple. Etiquete el diagrama de la derecha usando las mismas letras (\(\text{A}\)a través\(\text{J}\)) para mostrar que estas dos representaciones son verdaderamente isomórficas.
Usaremos el símbolo\(\mathbb{Z}^∗\) para referirnos al conjunto de todos los enteros excepto\(0\). Definir una relación\(\text{Q}\) en el conjunto de todos los pares en\(\mathbb{Z} × \mathbb{Z}^∗\) (pares de enteros donde la segunda coordenada es distinta de cero) por\((a, b)\text{Q}(c, d) \iff ad = bc\). Demostrar que\(\text{Q}\) es una relación de equivalencia.
La relación Q definida en el problema anterior divide el conjunto de todos los pares de enteros en un interesante conjunto de clases de equivalencia. Explicar por qué
\(\mathbb{Q} = (\mathbb{Z} × \mathbb{Z}^∗)/\text{Q}\).
En definitiva, ¡esta es la definición “correcta” del conjunto de números racionales!
Reflexionar sobre la prueba en problema 5. Tenga en cuenta que fuimos bastante cuidadosos al asegurar que la segunda coordenada en los pares ordenados es distinta de cero. (Esta fue toda la razón para introducir la\(\mathbb{Z}^∗\) notación.) ¿En qué momento del argumento utilizó esta hipótesis?


