6.4: Relaciones de Ordenamiento
- Page ID
- 114107
El prototipo para ordenar relaciones es\(≤\). Aunque se podría hacer un caso para su uso\(<\) como relación prototípica de ordenación. Estas dos relaciones difieren en un sentido importante:\(≤\) es reflexiva e\(<\) irreflexiva. Diversos autores, habiendo tomado diferentes elecciones en cuanto a cuál de ellas es la más prototípica, han definido las relaciones de ordenación de formas ligeramente diferentes. La opinión mayoritaria parece ser que una relación ordenadora es reflexiva (lo que significa que las relaciones de orden se modelan después\(≤\)). Realmente nos gustaría tomar la posición contraria —siempre apostamos por los desvalidos— pero una de nuestras relaciones de orden favoritas (divisibilidad) es reflexiva y sería eliminada si tomáramos la otra elección 1. Entonces...
Una relación\(\text{R}\) sobre un conjunto\(S\) es una relación de orden si\(\text{R}\) es reflexiva, antisimétrica y transitiva
Ahora bien, hemos utilizado\(≤\) para decidir qué propiedades debería tener una relación de orden, pero debemos señalar que la mayoría de las relaciones ordenadoras no hacen un trabajo tan bueno como\(≤\) lo hace. La\(≤\) relación impone lo que se conoce como un orden total a los conjuntos sobre los que actúa (debes tener en cuenta que no se puede usar para comparar números complejos, sino que se puede colocar entre reales o cualquiera de los conjuntos de números que están contenidos en\(\mathbb{R}\).) La mayoría de las relaciones ordenadoras solo crean lo que se conoce como un orden parcial en los conjuntos sobre los que actúan. En un orden total (también conocido como un ordenamiento lineal) cada par de elementos se puede comparar y podemos usar la relación de orden para decidir en qué orden van. En un ordenamiento parcial puede haber elementos que son incomparables.
Si\(x\) y\(y\) son elementos de un conjunto\(S\) y\(\text{R}\) es una relación de orden en\(S\) entonces decimos\(x\) y\(y\) son comparables si\(x\text{R}y ∨ y\text{R}x\).
Si\(x\) y\(y\) son elementos de un conjunto\(S\) y\(\text{R}\) es una relación ordenadora en\(S\) entonces decimos\(x\) y\(y\) son incomparables si ni\(x\text{R}y\) ni\(y\text{R}x\) es verdad.
Considera el conjunto\(S = \{1, 2, 3, 4, 6, 12\}\). Si miramos la relación\(≤\) en este set obtenemos el siguiente dígrafo.
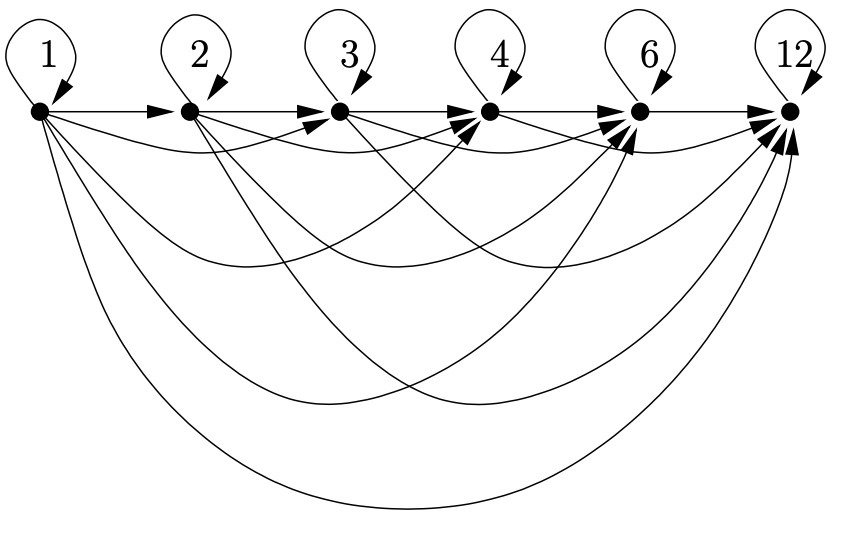
Por otro lado, quizá notó que estos números son los divisores de\(12\). La relación de divisibilidad nos dará nuestro primer ejemplo de un orden parcial.
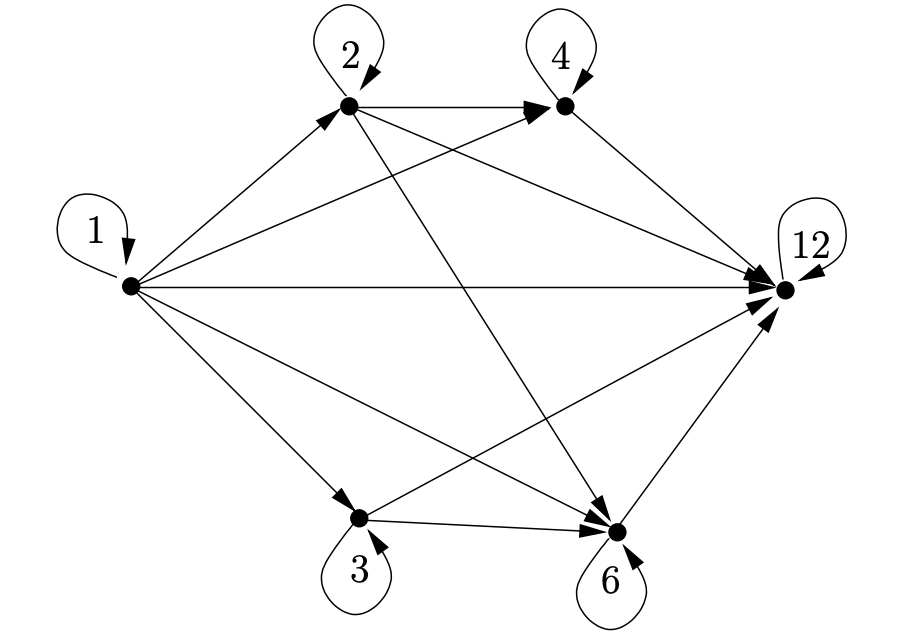
¿Qué elementos en el orden parcial anterior son incomparables?
Un conjunto junto con una relación de ordenación crea una estructura matemática conocida como conjunto parcialmente ordenado. Como eso es un poco bocado, el poset de forma abreviada en realidad se escucha con más frecuencia. Si se desea hacer referencia a un poset es necesario identificar tanto el conjunto como la relación de orden. Así, si\(S\) es un conjunto y\(\text{R}\) es una relación de orden, escribimos\((S, \text{R})\) para denotar el poset correspondiente.
Los dígrafos dados anteriormente para dos posets que tienen el mismo conjunto subyacente proporcionan una prueba de existencia — el mismo conjunto puede tener órdenes diferentes impuestas sobre él. También resaltan otro tema: ¡estos dígrafos para ordenar relaciones se abarrotan bastante! Los diagramas de Hasse para posets (que llevan el nombre del famoso matemático alemán Helmut Hasse) son una forma de mostrar toda la información en el dígrafo de un poset, pero mucho más sucintamente. Hay características de un diagrama de Hasse que corresponden a cada una de las propiedades que debe tener una relación de orden.
Dado que las relaciones de orden son siempre reflexivas, siempre habrá bucles en cada vértice del dígrafo. En un diagrama de Hasse, dejamos fuera los bucles.
Dado que las relaciones de orden son antisimétricas, cada borde en el dígrafo irá en una dirección u otra. En un diagrama de Hasse, organizamos los vértices para que esa dirección sea hacia arriba —de esa manera podemos dejar fuera todas las puntas de flecha sin perder ninguna información.
La simplificación final que hacemos al crear un diagrama de Hasse para un poset tiene que ver con la propiedad de transitividad —dejamos fuera cualquier conexión que pudiera deducirse por la transitividad.
Los diagramas de Hasse para los dos ordenamientos que hemos estado discutiendo se muestran en la Figura\(6.4.1\)
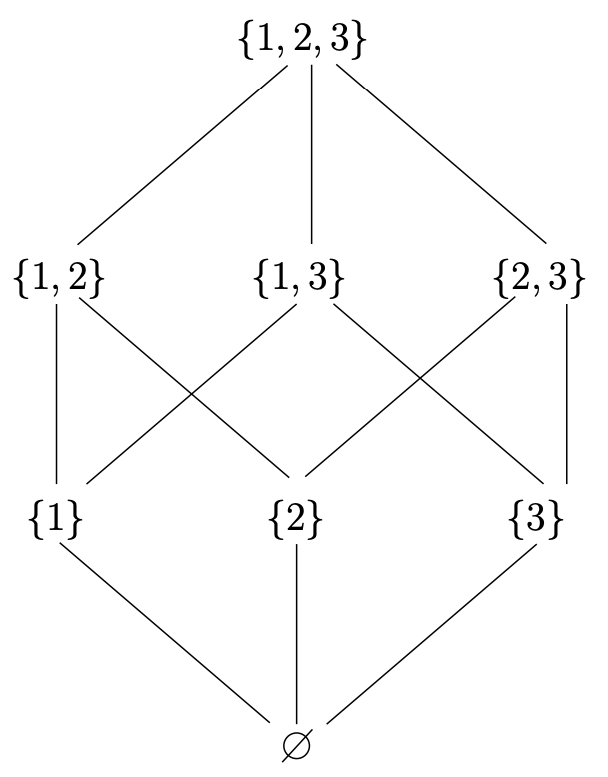
A menudo hay alguna característica de los elementos del conjunto que se están ordenando que nos permite organizar un diagrama de Hasse en “rangos”. Por ejemplo, considere\(P(\{1, 2, 3\})\), el conjunto de todos los subconjuntos de un conjunto de tres elementos — este conjunto se puede ordenar parcialmente usando la\(⊆\) relación. (Técnicamente, debemos verificar que esta relación es reflexiva, antisimétrica y transitiva antes de continuar, pero a estas alturas ya se sabe por qué la contención de subconjuntos se denota usando una versión redondeada de\(≤\).) ¡Los subconjuntos del mismo tamaño no pueden incluirse uno en el otro a menos que sean iguales! Esto nos permite dibujar el diagrama de Hasse para este conjunto con los nodos dispuestos en cuatro filas. (Ver Figura\(6.4.2\).)
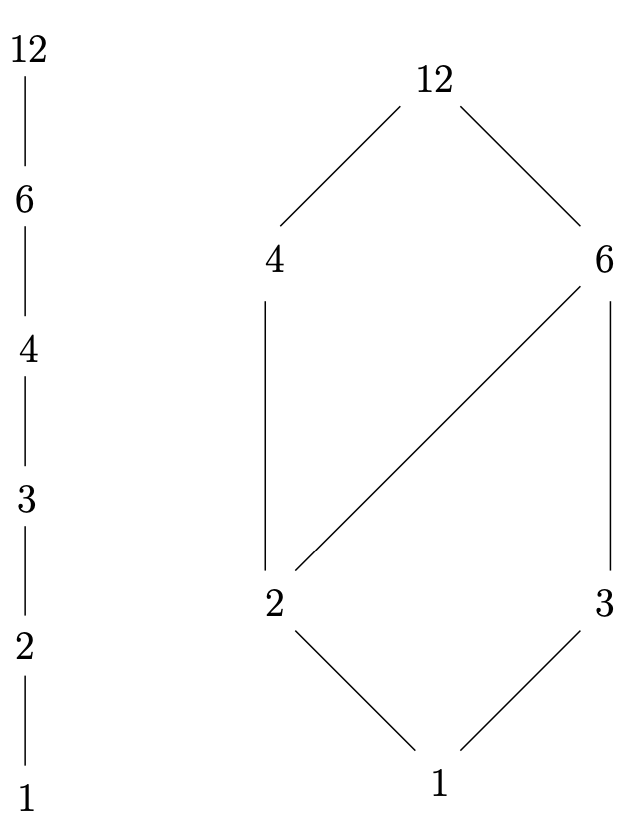
Intente dibujar un diagrama de Hasse para el conjunto parcialmente ordenado
\((P({1, 2, 3, 4}), ⊆)\).
Los posets como\((P({1, 2, 3}), ⊆)\) ese se pueden colocar en filas se conocen como posets graduados. Las cosas en un poset graduado que tienen el mismo rango son siempre incomparables.
Un poset calificado es un triple\((S, \text{R}, ρ)\), donde\(S\) es un conjunto,\(\text{R}\) es una relación de orden, y\(ρ\) es una función de\(S\) a\(\mathbb{Z}\).
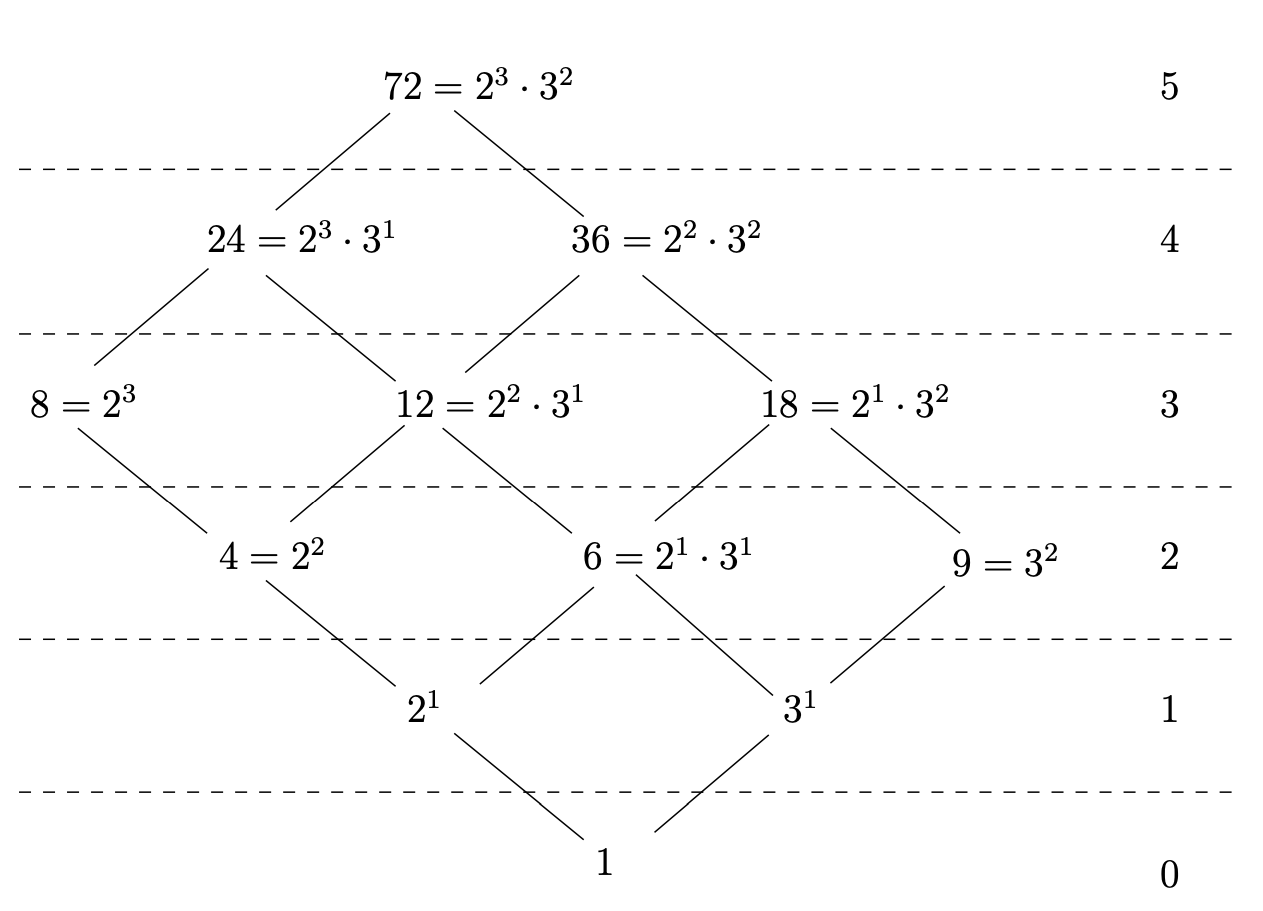
En el ejemplo que hemos estado considerando (el poset calificado de subconjuntos de un conjunto parcialmente ordenado por inclusión de conjuntos), la función de calificación\(ρ\) toma un subconjunto a su tamaño. Es decir,\(ρ(A) = |A|\). Otro buen ejemplo de un poset graduado es el conjunto de divisores de algún número parcialmente ordenados por la relación de divisibilidad (\(|\)). En este caso, la función de calificación lleva un número a su grado total, la suma de todos los exponentes que aparecen en su factorización prima. En la Figura\(6.4.3\) se muestra el poset de divisores de\(72\) e indicamos la gradación.
Terminaremos esta sección dando una pequeña colección de terminología relevante para conjuntos parcialmente ordenados.
Una cadena en un poset es un subconjunto de los elementos, todos los cuales son comparables. Si restringes tu atención a una cadena dentro de un poset, estarás viendo un pedido total. Una anticadena en un poset es un subconjunto de los elementos, ninguno de los cuales es comparable. Así, por ejemplo, un subconjunto de elementos que tienen el mismo rango (en un poset graduado) es una anticadena. Se dice que las cadenas y anticadena son máximas si no es posible añadirles más elementos (manteniendo las propiedades que las convierten en cadenas y/o anticadena). Se dice que un elemento\(x\), que aparece por encima de otro elemento\(y\) —y conectado a él— en un diagrama de Hasse lo cubre. Ante esta situación, también se puede decir que\(x\) es un sucesor inmediato de\(y\). Un elemento máximo es un elemento que no está cubierto por ningún otro elemento. De igual manera, un elemento mínimo es un elemento que no es una cubierta de ningún otro elemento. Si una cadena es máxima, se deduce que debe contener tanto un elemento máximo como un mínimo (con respecto al poset circundante). La colección de todos los elementos máximos forma una anticadena, al igual que (por separado) la colección de todos los elementos mínimos. Por último, tenemos las nociones de mayor elemento (a.k.a. top) y menos elemento (a.k.a. bottom) — el elemento más grande es mayor que cualquier otro elemento en el poset, el elemento menor es más pequeño que cualquier otro elemento. Por favor, tenga cuidado de distinguir estos conceptos de los elementos máximos y mínimos: un elemento mayor es automáticamente máximo, y un elemento mínimo siempre es mínimo, pero es posible tener un poset sin mayor elemento que, sin embargo, tenga uno o más elementos máximos, y es posible tener un poset sin menos elemento que tenga uno o más elementos mínimos.
En el poset de divisores de\(72\), el subconjunto\(\{2, 6, 12, 24\}\) es una cadena. Dado que sería posible sumar ambos\(1\) y\(72\) a esta cadena y aún tener una cadena, esta cadena no es máxima. (Pero, por supuesto, lo\(\{1, 2, 6, 12, 24, 72\}\) es.) Por otro lado,\(\{8, 12, 18\}\) es una anticadena (de hecho, esta es una anticadena máxima). Este poset tiene tanto una parte superior como una inferior\(1\) —es el elemento menor y\(72\) es el elemento más grande. Observe que los elementos que cubren\(1\) (el elemento mínimo) son los divisores primos de\(72\).
Ejercicios:
En la ecología poblacional hay un orden parcial “anterior” que básicamente significa que un organismo se alimenta de otro. Estrictamente hablando esta relación no es transitiva; sin embargo, si tomamos el punto de vista de que cuando un lobo come una oveja, también se está comiendo algo de la hierba de la que se ha alimentado la oveja, vemos que en cierto sentido es transitiva. Una cadena en este orden parcial se llama “cadena alimentaria” y se dice que los llamados depredadores ápice “se sientan en lo alto de la cadena alimentaria”. Así, “depredador ápice” es un término para un elemento máximo en este poset. Cuando venenos como el mercurio y los PCB se introducen en un ecosistema, tienden a acumularse desproporcionadamente en los depredadores ápice, razón por la cual las mujeres embarazadas y los niños pequeños no deben comer tiburón o atún sino que las sardinas están bien.
A continuación se muestra un pequeño ejemplo de una ecología parcialmente ordenada por “anteriores”
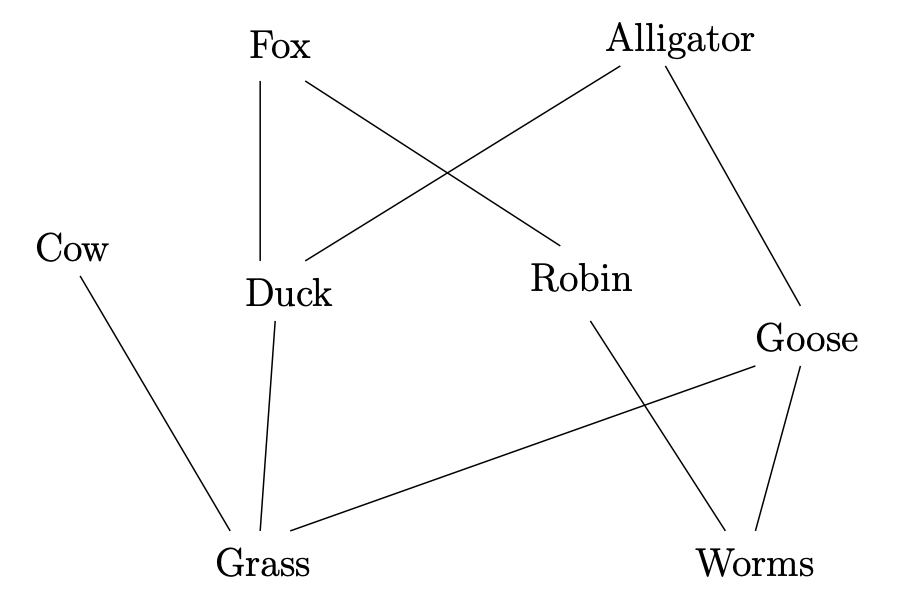
Encuentra el anticadena más grande en este poset.
En referencia al poset dado en Ejercicio\(6.4.1\), coincidir con lo siguiente.
1. Una anticadena a (no máxima).\(\text{Grass}\)
2. Una anticadena máxima b.\(\text{Goose}\)
3. Un elemento máximo c.\(\text{Fox}\)
4. Una cadena (no máxima) d.\(\{\text{Grass}, \text{ Duck}\}\)
5. Una cadena máxima e.\(\text{There isn’t one!}\)
6. Una portada para “Worms” f.\(\{\text{Fox}, \text{ Alligator}, \text{ Cow}\}\)
7. Al menos elemento g.\(\{\text{Cow}, \text{ Duck}, \text{ Goose}\}\)
8. Un elemento mínimo h.\(\{\text{Worms}, \text{ Robin}, \text{ Fox}\}\)
La gráfica de los bordes de un cubo es una en una secuencia infinita de gráficas. Estas gráficas se definen recursivamente por “Hacer dos copias de la gráfica anterior luego unir los nodos correspondientes en las dos copias con bordes”. El 'cubo'\(0\) dimensional es solo un punto único. El cubo\(1\) -dimensional es un solo borde con un nodo en cada extremo. El cubo\(2\) -dimensional es en realidad un cuadrado y el cubo\(3\) -dimensional es lo que generalmente queremos decir cuando decimos “cubo”.
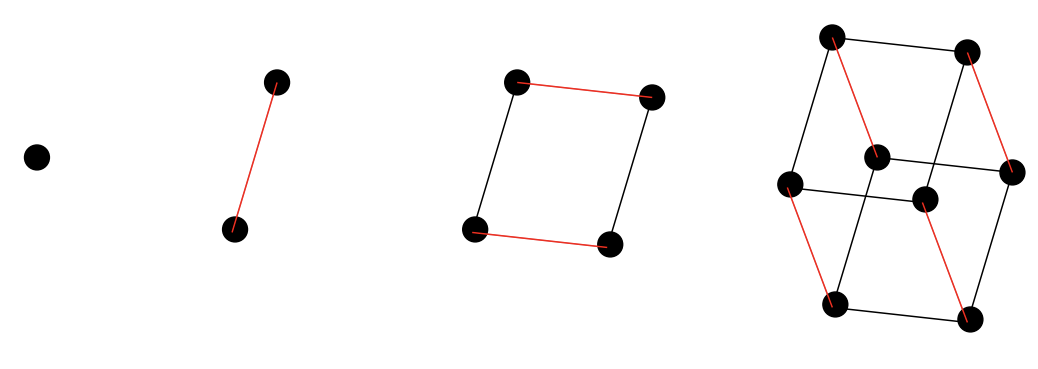
Haz un dibujo cuidadoso de un hipercubo —que es el nombre de la gráfica que sigue al cubo ordinario en esta secuencia.
Etiquetar los nodos de un hipercubo con los divisores\(210\) de para producir un diagrama Hasse del poset determinado por la relación de divisibilidad.
Etiquetar los nodos de un hipercubo con los subconjuntos\(\{a, b, c, d\}\) de para producir un diagrama Hasse del poset determinado por la relación de contención del subconjunto.
Completar un diagrama de Hasse para el poset de divisores de\(11025\) (parcialmente ordenados por divisibilidad).
Encuentra una colección de conjuntos para que, cuando estén parcialmente ordenados por\(⊆\), obtengamos el mismo diagrama de Hasse que en el problema anterior.


