6.5: Funciones
- Page ID
- 114092
El concepto de función es una de las abstracciones más útiles en matemáticas. De hecho, ¡es una abstracción que se puede abstraer aún más! Por ejemplo, un operador es una entidad que toma funciones como entradas y produce funciones como salidas, por lo que un operador es para funciones como funciones en sí mismas son para números. Hay muchos operadores con los que sin duda ya te has encontrado —pero no con ese nombre. Uno de los operadores más famosos es la “diferenciación”, cuando tomas la derivada de alguna función, la respuesta que obtienes es otra función. Si a dos personas diferentes se les da el mismo problema de diferenciación y se les ocurren respuestas diferentes, ¡sabemos que al menos una de ellas ha cometido un error! Del mismo modo, si se hacen dos cálculos del valor de una función para la misma entrada, deben coincidir.
La propiedad que estamos discutiendo solía ser capturada diciendo que una función necesita estar “bien definida”. La definición de la vieja escuela de una función era:
Una función\(f\) es una regla bien definida, que, dado cualquier valor de entrada\(x\) produce un valor único de salida 1\(f(x)\).
Una definición más moderna de una función es la siguiente.
Una función es una relación binaria que no contiene pares distintos que tengan el mismo elemento inicial.
Cuando pensamos en una función como un tipo especial de relación binaria, los pares que están “en” la función tienen la forma\((x, f(x))\), es decir, consisten en una entrada y la salida correspondiente.
Nos hemos acostumbrado relativamente a las relaciones “en” un conjunto, pero recordemos que la situación más general es que una relación binaria es un subconjunto de\(A × B\). En esta configuración, si la relación es en realidad una función\(f\), decimos que\(f\) es una función de\(A\) a\(B\). Ahora bien, muy a menudo hay valores de entrada que simplemente no funcionan para una función determinada (por ejemplo, la conocida regla de “no puedes tomar la raíz cuadrada de una negativa”). Además, suele darse el caso de que ciertas salidas simplemente no pueden suceder. Entonces, cuando se trata de una función como una relación contenida en en realidad\(A × B\) hay cuatro conjuntos que son de interés — los conjuntos\(A\) y\(B\) (por supuesto) pero también algunos conjuntos que vamos a denotar por\(A'\) y\(B'\). El conjunto\(A'\) consiste en aquellos elementos de los\(A\) que realmente aparecen como la primera coordenada de un par en la relación\(f\). El conjunto\(B'\) consiste en aquellos elementos de los\(B\) que realmente aparecen como la segunda coordenada de un par en la relación\(f\). Un ejemplo genérico de cómo podrían verse estos cuatro conjuntos se da en la Figura\(6.5.1\).
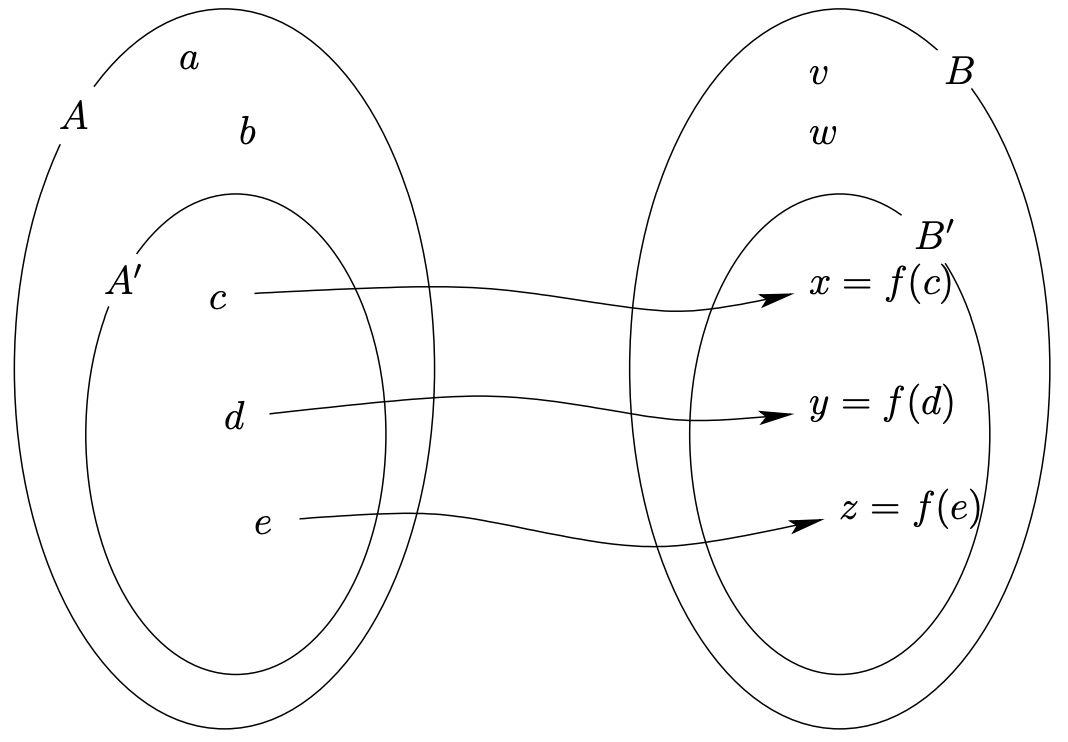
Lamentablemente, sólo tres de los conjuntos que acabamos de discutir son conocidos por el mundo matemático. El conjunto que hemos denotado\(A'\) se llama el dominio de la función\(f\). El conjunto que hemos denotado\(B'\) se conoce como el rango de la función\(f\). El conjunto que hemos denotado\(B\) se llama el codominio de la función\(f\). El set al que hemos estado llamando\(A\) no tiene nombre. De hecho, la definición formal del término “función” ha sido amañada para que no haya diferencia entre los conjuntos\(A\) y\(A'\). Esto parece una pena, si piensas en el rango y el dominio como primarios, ¿no parece extraño que tengamos una manera de referirnos a un superconjunto del rango (es decir, el codominio) pero no forma de referirnos a un superconjunto del dominio?
No obstante, así es como es. Solo hay un conjunto en el lado de entrada: el dominio de nuestra función.
El dominio de cualquier relación se expresa por escrito\(\text{Dom}(\text{R})\). Que se define de la siguiente manera.
Si\(\text{R}\) es una relación de\(A\) a\(B\) entonces\(\text{Dom}(\text{R})\) es un subconjunto de\(A\) definido por
\[\text{Dom}(\text{R}) = \{a ∈ A ∃b ∈ B,(a, b) ∈ R\}\]
Debemos señalar que la notación que se acaba de dar para el dominio de una relación\(\text{R}\),\(\text{Dom}(\text{R})\) tiene análogos para los otros conjuntos que están involucrados con una relación. Escribimos\(\text{Cod}(\text{R})\) para referir el codominio de la relación, y\(\text{Rng}(\text{R})\) para referirnos al rango.
Como ahora estamos pensando en las funciones como clases especiales de relaciones, se deduce que una función es solo un conjunto de pares ordenados. Esto significa que la identidad de una función está ligada, no solo con una fórmula que da la salida para una entrada dada, sino también con qué valores se pueden usar para esas entradas. Así, la función\(f(x) = 2x\) definida en\(\mathbb{R}\) es un animal completamente diferente de la función\(f(x) = 2x\) definida en\(\mathbb{N}\). Si realmente quieres especificar una función con precisión debes dar su dominio así como una fórmula para ello. Por lo general, se hace esto escribiendo una fórmula, luego un punto y coma, luego el dominio. (Por ejemplo)\(f(x) = x^2 ; x ≥ 0\)
Bien, entonces, finalmente, estamos preparados para dar la definición real de una función.
Si\(A\) y\(B\) son conjuntos, entonces\(f\) es una función de\(A\) a\(B\) (que se expresa simbólicamente por\(f : A \longrightarrow B\)), si y solo si\(f\) es un subconjunto de\(A × B\),\(\text{Dom}(f) = A\) y\(((a, b) ∈ f ∧ (a, c) ∈ f \implies b = c\).
Recapitulando, una función debe tener su dominio igual al conjunto de\(A\) donde provienen sus entradas. Esto a veces se expresa diciendo que una función se define en su dominio. Sin embargo, el rango y el codominio de una función pueden ser diferentes. En el caso de que el rango y el codominio sean los mismos\((\text{Cod}(\text{R}) = \text{Rng}(\text{R}))\) tenemos una situación bastante especial y la función es agraciada por la denominación “sobrejección”. El término “onto” también se usa comúnmente para describir una función suryectiva.
Hay una expresión en las matemáticas, “Cada función está en su rango”. eso realmente no dice mucho. ¿Por qué no?
Si uno tiene elementos x e y, del dominio y codominio, (respectivamente) y\(y = f(x)\) 2 entonces se puede decir que “\(y\)es la imagen de\(x\)” o que “\(x\)es una preimagen de”\(y\). Toma nota cuidadosa de los artículos utilizados en estas frases — decimos “\(y\)es la imagen de\(x\)” pero “\(x\)es una preimagen de”\(y\). Esto se debe a que\(y\) está determinado de manera única por\(x\), pero no al revés. Por ejemplo, ya que los cuadrados de\(2\) y\(−2\) son ambos\(4\), si consideramos la función\(f(x) = x^2\), la imagen de (digamos)\(2\) es\(4\), pero una preimagen para\(4\) podría ser cualquiera\(2\) o\(−2\).
Sería agradable si hubiera una buena manera de referirse a la preimagen de algún elemento,\(y\), de la gama. Una notación que probablemente hayas visto antes es “\(f^{−1} (y)\).” Hay una gran dificultad para anotar tal cosa. Al escribir “\(f^{−1}\)” estás haciendo una presunción bastante vasta —que en realidad hay una función que sirve de inversa para\(f\). Por lo general, no la hay.
Se puede definir una inversa para cualquier relación, la inversa se forma simplemente intercambiando los elementos en los pares ordenados que componen\(\text{R}\).
La relación inversa de una relación\(\text{R}\) se denota\(\text{R}^{−1}\) y
\[\text{R}^{−1} = \{(y, x) (x, y) ∈ \text{R}\}.\]
En cuanto a las gráficas, la relación inversa y la original se relacionan por ser reflexiones en la línea\(y = x\). Es posible que una, ambas, o ninguna de estas sean funciones. El ejemplo canónico a tener en cuenta es probablemente\(f(x) = x^2\) y su inverso.
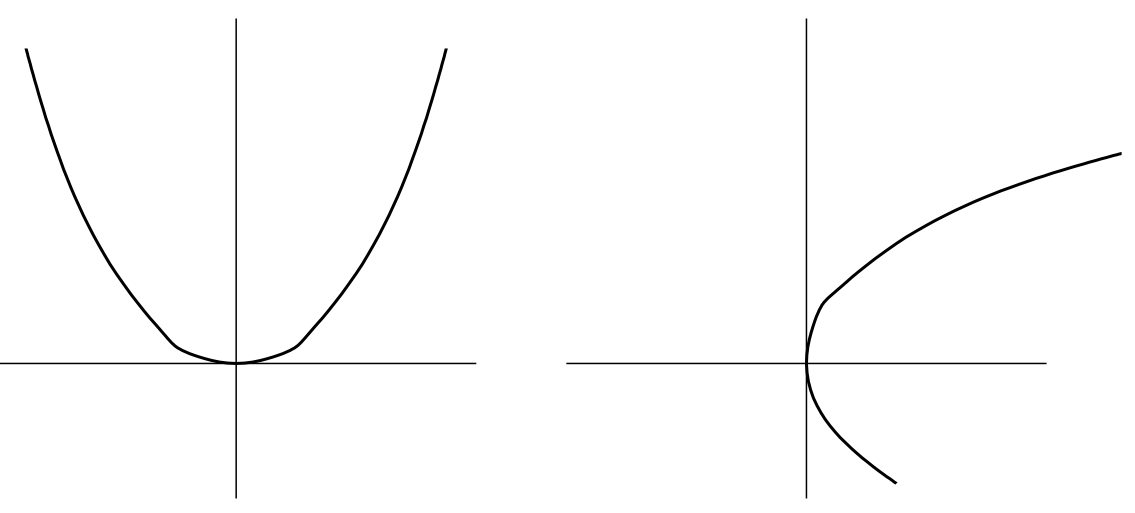
La gráfica que obtenemos reflejando\(y = f(x) = x^2\) en la línea\(y = x\) no pasa la prueba de línea vertical y por lo tanto es la gráfica de (meramente) una relación —no de una función—. La función\(g(x) = \sqrt{x}\) que todos conocemos y amamos no es realmente la inversa de\(f(x)\). De hecho, esta función se define para hacer una elección específica (y natural) — devuelve la raíz cuadrada positiva de un número. Pero esto lleva a un problema sutil; si empezamos con un número negativo (digamos\(−3\)) y lo cuadramos obtenemos un número positivo (\(9\)) y si luego venimos y tomamos la raíz cuadrada obtenemos otro número positivo (\(3\)). Esto es problemático ya que no terminamos por donde empezamos que es lo que debería suceder si aplicamos una función seguida de su inversa.
Intentaremos manejar la situación general en un poco, pero por el momento consideremos el buen caso: cuando la inversa de una función también es una función. ¿Cuándo exactamente sucede esto? Bueno, acabamos de ver que la inversa de una función no necesariamente pasa la prueba de línea vertical, y resulta que ese es el tema predominante. Entonces, ¿bajo qué circunstancias pasa la inversa la prueba de línea vertical? Cuando la función original pasa la llamada prueba de línea horizontal (cada línea horizontal cruza la gráfica como máximo una vez). Pensando de nuevo en ello\(f(x) = x^2\), hay algunas líneas horizontales que extrañan la gráfica por completo, pero todas las líneas horizontales de la forma\(y = c\) donde\(c\) es positiva se cruzarán con la gráfica dos veces. Hay muchas funciones que sí pasan la prueba de línea horizontal, por ejemplo, considere\(f(x) = x^3\). Tales funciones se conocen como inyecciones, esto es lo mismo que decir que una función es “uno-toone”. Las funciones inyectoras se pueden invertir — el dominio de la función inversa de solo\(f\) será el rango,\(\text{Rng}(f)\), que como hemos visto puede quedar por debajo del ser todo el codominio, ya que\(\text{Rng}(f) ⊆ \text{Cod}(f)\).
Primero definamos las inyecciones de una manera que esté divorciada de pensar en sus gráficas.
Una función\(f(x)\) es una inyección iff para todos los pares de entradas\(x_1\) y\(x_2\), si es\(f(x_1) = f(x_2)\) entonces\(x_1 = x_2\).
Esta es otra de esas propiedades definitorias que está diseñada para que cuando sea verdad sea vacuamente cierta. Una función de inyección nunca toma dos entradas distintas a la misma salida. Quizás la forma más limpia de pensar sobre las funciones inyectoras es en términos de preimágenes: cuando una función es inyectable, las preimágenes son únicas. En realidad, este es un buen momento para mencionar algo sobre las funciones suryectivas y las preimágenes —si una función es suryectiva, cada elemento del codominio tiene una preimagen. Entonces, si una función tiene ambas propiedades significa que cada elemento del codominio tiene una (y solo una) preimagen.
Una función que es tanto inyectiva como suryectiva (uno a uno y sobre) se conoce como biyección. Las bijecciones son tremendamente importantes en matemáticas ya que proporcionan una manera de emparejar perfectamente los elementos de dos conjuntos. Probablemente pasarás un buen rato en el futuro ideando mapas entre sets y luego demostrando que son bijecciones, así que empezaremos a practicar esa habilidad ahora.
Ordinariamente, mostraremos que una función es una biyección demostrando por separado que es tanto una sobreyección como una inyección.
Para demostrar que una función es suryectiva necesitamos demostrar que es posible encontrar una preimagen para cada elemento del codominio. Si por casualidad sabemos cuál es la función inversa, entonces es fácil encontrar una preimagen para un elemento arbitrario. En cuanto a la taxonomía de pruebas que se introdujo en el Capítulo 3, estamos hablando de una prueba constructiva de una afirmación existencial. Una función\(f\) es suryectiva iff\(∀y ∈ \text{Cod}(f), ∃x ∈ \text{Dom}(f)\),\(y = f(x)\), así que probar surjectividad es encontrar la\(x\) que “funciona” para una arbitraria\(y\). Si esto se hace literalmente nombrando\(x\), hemos probado la afirmación de manera constructiva.
Para demostrar que una función es una inyección, tradicionalmente probamos que la propiedad utilizada en la definición de una función inyectora es verdadera. Es decir, suponemos que\(x_1\) y\(x_2\) son elementos distintos de\(\text{Dom}(f)\) y eso\(f(x_1) = f(x_2)\) y luego lo demostramos en realidad\(x_1 = x_2\). Esto está en el espíritu de una prueba por contradicción —si en realidad hubiera elementos distintos que se mapearan al mismo valor entonces no\(f\) serían inyectables, sino deduciendo que\(x_1 = x_2\) estamos contradiciendo esa presunción y así, estamos demostrando que efectivamente\(f\) es una inyección.
Empecemos por mirar un ejemplo muy sencillo,\(f(x) = 2x − 1\);\(x ∈ \mathbb{N}\). Claramente esta función no es una surjección si estamos pensando que\(\text{Cod}(f) = \mathbb{N}\) ya que las salidas son siempre impares. Dejado\(\mathcal{O} = \{1, 3, 5, 7, . . .\}\) ser el conjunto de naturales impares.
La función\(f : \mathbb{N} \implies \mathcal{O}\) definida por\(f(x) = 2x − 1\) es una biyección de\(\mathbb{N}\) a\(\mathcal{O}\).
- Prueba
-
Primero mostraremos que\(f\) es suryectiva. Considera un elemento arbitrario\(y\) del conjunto\(\mathcal{O}\). Ya que\(y ∈ \mathcal{O}\) se deduce que\(y\) es tanto positivo como impar. Así hay un entero\(k\), tal que\(y = 2k + 1\), pero también\(y > 0\). De esto se deduce eso\(2k + 1 > 0\) y así\(k > −\dfrac{1}{2}\). Dado que también\(k\) es un número entero, esta última desigualdad implica eso\(k ∈ \mathbb{Z}^{\text{noneg}}\). (Recordemos eso\(\mathbb{Z}^{\text{noneg}} = \{0, 1, 2, 3, . . .\}\).) Podemos verificar fácilmente que una preimagen para\(y\) es\(k + 1\), ya que\(f(k + 1) = 2(k + 1) − 1 = 2k + 2 − 1 = 2k + 1 = y\).
A continuación mostramos que\(f\) es inyectable. Supongamos que hay dos valores de entrada,\(x_1\) y\(x_2\) tal que\(f(x_1) = f(x_2)\). Entonces\(2x_1−1 = 2x_2−1\) y álgebra simple conduce a\(x_1 = x_2\).
Q.E.D.
Para un ejemplo un poco más complicado considera la función de\(\mathbb{N}\) a\(\mathbb{Z}\) definida por
\[ f(x)=\begin{cases} \dfrac{x}{2}\;\;\;\;\;\;\;\;\;\;\;\; \text{ if } x \text{ is even } \\ −\dfrac{(x − 1)}{2} \;\; \text{ if } x \text{ is odd } \end{cases}\]
Esta función hace un pequeño trabajo bastante útil, empareja los números naturales y los enteros en pares. Cada natural par se empareja con un entero positivo y cada natural impar (excepto\(1\)) se empareja con un entero negativo (\(1\)se empareja con\(0\)). Esta función realmente está haciendo algo notable: el sentido común parecería indicar que los enteros deben ser un conjunto mayor que los naturales (después de todo\(\mathbb{N}\) está completamente contenido dentro de\(\mathbb{Z}\)), pero la función f definida anteriormente sirve para mostrar que estos dos conjuntos son exactamente los ¡mismo tamaño!
La función\(f\) definida anteriormente es biyectiva.
- Prueba
-
Primero mostraremos que\(f\) es suryectiva.
Basta con encontrar una preimagen para un elemento arbitrario de\(\mathbb{Z}\). Supongamos que\(y\) es un entero particular pero arbitrariamente elegido. Hay dos casos a considerar:\(y ≤ 0\) y\(y > 0\).
Si\(y > 0\) entonces\(x = 2y\) es una preimagen para\(y\). Esto sigue fácilmente ya que obviamente\(x = 2y\) es parejo y así\(x\) la imagen será definida por el primer caso en la definición de\(f\). Así\(f(x) = f(2y) = \dfrac{(2y)}{2} = y\).
Si\(y ≤ 0\) entonces\(x = 1 − 2y\) es una preimagen para\(y\). Claramente,\(1 − 2y\) es impar siempre que sea\(y\) un entero, así este valor para\(x\) caerá en el segundo caso en la definición de\(f\). Entonces,\(f(x) = f(1 − 2y) = −\dfrac{((1 − 2y) − 1)}{2} = −\dfrac{(−2y)}{2} = y\).
Dado que los casos\(y > 0\) y\(y ≤ 0\) son exhaustivos (es decir, cada\(y\) en\(\mathbb{Z}\) cae en uno u otro de estos casos), y hemos encontrado una preimagen para\(y\) en ambos casos, se deduce que\(f\) es suryectiva.
A continuación, mostraremos que\(f\) es inyectivo.
Supongamos que\(x_1\) y\(x_2\) son elementos de\(\mathbb{N}\) y eso\(f(x_1) = f(x_2)\). Considera los tres casos siguientes:\(x_1\) y ambos\(x_2\) son pares, ambos impares, o tienen paridad opuesta.
Si\(x_1\) y\(x_2\) son ambos parejos, entonces por la definición de\(f\) tenemos\(f(x_1) = \dfrac{x_1}{2}\)\(f(x_2) = \dfrac{x_2}{2}\) y y como estos valores funcionales son iguales, tenemos\(\dfrac{x_1}{2} = \dfrac{x_2}{2}\). Duplicar ambos lados de esto conduce a\(x_1 = x_2\).
Si\(x_1\) y ambos\(x_2\) son impares, entonces por la definición de\(f\) tenemos\(f(x_1) = −\dfrac{(x_1 − 1)}{2}\)\(f(x_2) = −\dfrac{(x_2 − 1)}{2}\) y y como estos valores funcionales son iguales, tenemos\(−\dfrac{(x_1 − 1)}{2} = −\dfrac{(x_2 − 1)}{2}\). Un poco más álgebra (duplicar, negar y agregar uno a ambos lados) conduce a\(x_1 = x_2\).
Si\(x_1\) y\(x_2\) tenemos paridad opuesta, asumiremos w.l.o.g. que\(x_1\) es par y\(x_2\) es impar. La igualdad\(f(x_1) = f(x_2)\) se vuelve\(\dfrac{x_1}{2} = −\dfrac{(x_2 − 1)}{2}\). Tenga en cuenta que\(x_1 ≥ 2\) así\(f(x_1) = \dfrac{x_1}{2} ≥ 1\). Además, tenga en cuenta\(x_2 ≥ 1\) que
\(x_2 − 1 ≥ 0 \\ (\dfrac{(x_2 − 1)}{2} ≥ 0 \\ −\dfrac{(x_2 − 1)}{2} ≤ 0 \\ f(x_2) ≤ 0\)
por lo tanto tenemos una contradicción ya que es imposible que los dos valores\(f(x_1)\) y\(f(x_2)\) sean iguales mientras\(f(x_1) ≥ 1\) y\(f(x_2) ≤ 0\).
Dado que el último caso que se examina lleva a una contradicción, se deduce que\(x_1\) y\(x_2\) nunca tienen paridades opuestas, y así los dos primeros casos son exhaustivos —en ambos casos, llegamos a la conclusión deseada de que\(x_1 = x_2\) así se deduce que f es inyectable.
Q.E.D.
Concluiremos esta sección mencionando que las ideas de “imagen” y “preimagen” se pueden extender a conjuntos. Si\(S\) es un subconjunto de\(\text{Dom}(f)\) entonces la imagen de\(S\) debajo\(f\) se denota\(f(S)\) y
\[f(S) = \{y | ∃x ∈ \text{Dom}(f), x ∈ S ∧ y = f(x)\}.\]
Del mismo modo, si\(T\) es un subconjunto de\(\text{Rng}(f)\) podemos definir algo parecido a la preimagen. La imagen inversa del conjunto\(T\) bajo la función\(f\) se denota\(f^{−1} (T)\) y
\[f^{−1} (T) = \{x | ∃y ∈ \text{Cod}(f), y ∈ T ∧ y = f(x)\}.\]
Esencialmente, ¡hemos ampliado la función\(f\) para que vaya entre los conjuntos de potencia de su codominio y rango! Esta nueva noción nos da algunas formas elegantes de reafirmar lo que significa ser suryectiva e inyectable. Una función\(f\) es suryectiva iff\(f(\text{Dom}(f)) = \text{Cod}(f)\). Una función\(f\) es inyectiva si las imágenes inversas de los singletones son siempre singletones. Es decir,
\[∀y ∈ \text{Rng}(f), ∃x ∈ \text{Dom}(f), f^{−1} ({y}) = {x}.\]
Ejercicios:
Para cada una de las siguientes funciones, dar su dominio, rango y un posible codominio.
- \(f(x) = \sin (x)\)
- \(g(x) = e^x\)
- \(h(x) = x^2\)
- \(m(x) = \dfrac{x^2+1}{x^2−1}\)
- \(n(x) = \lfloor x \rfloor\)
- \(p(x) = \langle \cos (x), \sin (x) \rangle\)
Encuentra una biyección del conjunto de cuadrados impares\(\{1, 9, 25, 49, . . .\}\),, a los enteros no negativos,\(\mathbb{Z}^{\text{noneg}} = \{0, 1, 2, 3, . . .\}\). Demuestra que la función que acabas de determinar es a la vez inyectiva y suryectiva. Encuentra la función inversa de la biyección anterior.
La función de logaritmo natural\(\ln(x)\) se define por una integral definida con la variable\(x\) en el límite superior.
\(ln(x) = \int_{t=1}^{x} \dfrac{1}{t} dt.\)
De esta definición podemos deducir que\(\ln(x)\) está aumentando estrictamente en todo su dominio,\((0,∞).\) ¿por qué es esto cierto?
Podemos usar la definición anterior con\(x = 2\) para encontrar el valor de\(\ln(2) ≈ .693\). También tomaremos como se da la siguiente regla (que es válida para todas las funciones logarítmicas).
\(\ln(a^b) = b \ln(a)\)
Utilice la información anterior para mostrar que no existe ni un límite superior ni un límite inferior para los valores del logaritmo natural. Estos hechos junto con la información que ln está aumentando estrictamente lo demuestran\(\text{Rng}(\ln) = \mathbb{R}\).
Georg Cantor desarrolló una forma sistemática de enumerar los números racionales. Al “enumerar” un conjunto uno en realidad está desarrollando una bijección de\(\mathbb{N}\) a ese conjunto. El método conocido como “Serpiente de Cantor” crea una bijección desde los naturales hasta los racionales no negativos. Primero, creamos una tabla infinita cuyas filas están indexadas por enteros positivos y cuyas columnas están indexadas por enteros no negativos — las entradas en esta tabla son números racionales de la forma “índice de columna”/“índice de fila”. Luego seguimos un camino similar a una serpiente que zig-zaga a través de esta tabla —cada vez que encontramos un número racional que no hemos visto antes (en términos inferiores) lo escribimos. Esto se indica en el siguiente diagrama dando vueltas a las entradas.
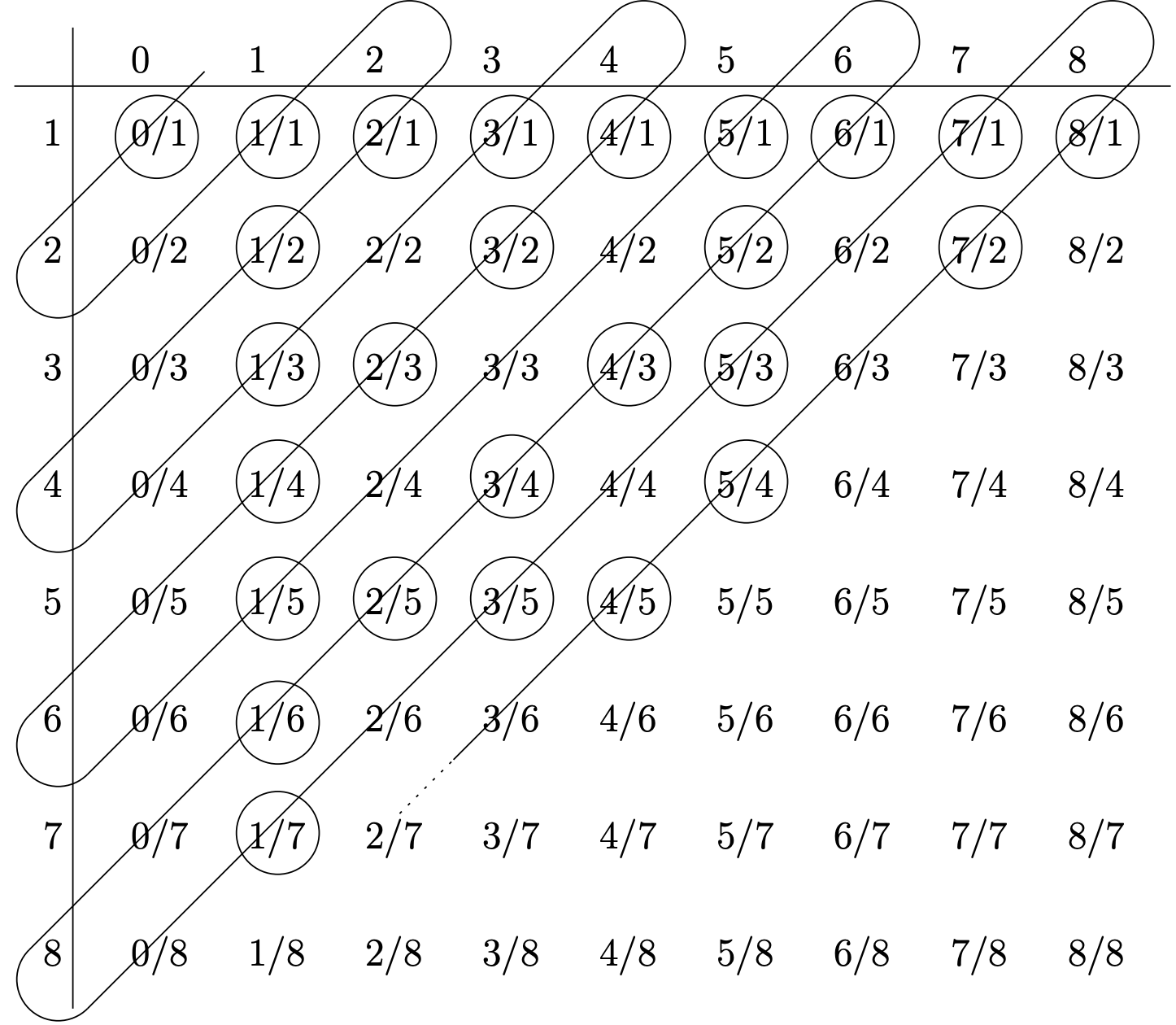
Efectivamente esto nos da una función\(f\) que produce el número racional que se encontraría en una posición dada en esta lista. Por ejemplo\(f(1) = \dfrac{0}{1}\),\(f(2) = \dfrac{1}{1}\) y\(f(5) = \dfrac{1}{3}\).
¿Qué es\(f(26)\)? ¿Qué es\(f(30)\)? ¿Qué es\(f^{−1} \left( \dfrac{3}{4} \right)\)? ¿Qué es\(f^{−1} \left( \dfrac{6}{7} \right)\)?


