7.2: Argumentos de paridad y conteo
- Page ID
- 113966
Esta sección se ocupa de dos elementos muy poderosos del arsenal de pruebas: “Paridad” es una forma de referirse al resultado de un cálculo par/impar; Contar argumentos que suelen tomar la forma de contar alguna colección de dos maneras distintas —y luego comparar esos resultados. Estas técnicas tienen poco que ver entre sí, pero cuando son aplicables tienden a producir pequeños argumentos realmente elegantes.
En las computadoras (muy) tempranas y máquinas comerciales, se utilizaron tarjetas de papel para almacenar información. Se utilizó una llamada “tarjeta perforadora” o “tarjeta Hollerith” para almacenar información binaria por medio de agujeros perforados en ella. También se utilizó cinta de papel de manera similar. Un formato típico de cinta de papel implicaría\(8\) posiciones en filas a lo largo de la cinta que podrían o no ser perforadas, a menudo también aparecería una columna de agujeros más pequeños que no almacenaba información sino que se usaban para impulsar la cinta a través del mecanismo de lectura en una rueda dentada. Las cintas y tarjetas podrían ser “leídas” ya sea por pequeños conjuntos de contactos eléctricos que tocarían a través de un agujero perforado o se mantendrían separados si la posición no se perforaba, o usando un fotodetector para detectar si la luz podría pasar a través del orificio o no. Los mecanismos para leer y escribir en estos medios de papel eran increíblemente precisos y permitían que las primeras máquinas de procesamiento de datos usaran solo un par de archivadores grandes para almacenar lo que ahora cabe en una unidad de salto que uno puede usar en un collar. (Acerca\(10\) o\(12\) gabinetes podrían contener un gigabyte de datos).
Los medios de papel eran ideales para almacenar información binaria, pero por supuesto la mayoría de los datos reales que la gente necesitaba almacenar y procesar serían alfanuméricos 1. Hubo varios esquemas de codificación que sirvieron para traducir entre los conjuntos de caracteres que la gente usaba comúnmente y los números binarios que podían almacenarse en papel. Uno de estos esquemas aún sobrevive hoy — ASCII. El American Standard Code for Information Interchange utiliza números binarios de\(7\) -bit para representar caracteres, por lo que contiene\(128\) diferentes símbolos. Esto es más que suficiente para representar letras mayúsculas y minúsculas, los\(10\) números y los signos de puntuación; muchos de los puntos restantes en el código ASCII se usaron para contener los llamados “caracteres de control” que estaban asociados con la funcionalidad que aparecía en el teletipo anticuado equipo — cosas como “tocar la campana”, “mover el carro hacia atrás un espacio”, “mover el carro a la siguiente línea”, etc. Estos caracteres de control son la razón por la que los teclados modernos todavía tienen una tecla modificador etiquetada como “Ctrl” en ellos. El siguiente listado da los números decimales y binarios de\(0\) a\(127\) y los caracteres ASCII asociados con ellos; los caracteres no impresos y de control tienen una designación mnemotécnica\(2\) o\(3\) letra.
\(\begin{array} &0\;\;\;\;\; &0000\; 0000\;\;\;\;\; &\text{NUL}\;\;\;\;\;\;\;\;\;\; &64\;\;\;\;\; &0100\; 0000\;\;\;\;\; &@ \\ 1\;\;\;\;\; &0000\; 0001 \;\;\;\;\;&\text{SOH}\;\;\;\;\;\;\;\;\;\; &65\;\;\;\;\; &0100\; 0001\;\;\;\;\; &\text{A}\\ 2\;\;\;\;\; &0000\; 0010 \;\;\;\;\;&\text{STX}\;\;\;\;\;\;\;\;\;\; &66\;\;\;\;\; &0100\; 0010\;\;\;\;\; &\text{B}\\ 3\;\;\;\;\; &0000\; 0011 \;\;\;\;\;&\text{ETX}\;\;\;\;\;\;\;\;\;\; &67\;\;\;\;\; &0100\; 0011\;\;\;\;\; &\text{C}\\ 4\;\;\;\;\; &0000\; 0100 \;\;\;\;\;&\text{EOT}\;\;\;\;\;\;\;\;\;\; &68\;\;\;\;\; &0100\; 0100\;\;\;\;\; &\text{D}\\ 5\;\;\;\;\; &0000\; 0101 \;\;\;\;\;&\text{ENQ}\;\;\;\;\;\;\;\;\;\; &69\;\;\;\;\; &0100\; 0101\;\;\;\;\; &\text{E}\\ 6\;\;\;\;\; &0000\; 0110 \;\;\;\;\;&\text{ACK}\;\;\;\;\;\;\;\;\;\; &70\;\;\;\;\; &0100 \;0110\;\;\;\;\; &\text{F}\\ 7\;\;\;\;\; &0000\; 0111 \;\;\;\;\;&\text{BEL}\;\;\;\;\;\;\;\;\;\; &71\;\;\;\;\; &0100 \;0111\;\;\;\;\; &\text{G}\\ 8\;\;\;\;\; &0000\; 1000 \;\;\;\;\;&\text{BS}\;\;\;\;\;\;\;\;\;\; &72\;\;\;\;\; &0100 \;1000\;\;\;\;\; &\text{H}\\ 9\;\;\;\;\; &0000\; 1001 \;\;\;\;\;&\text{TAB}\;\;\;\;\;\;\;\;\;\; &73\;\;\;\;\; &0100\; 1001\;\;\;\;\; &\text{I}\\ 10\;\;\;\;\; &0000\; 1010 \;\;\;\;\;&\text{LF}\;\;\;\;\;\;\;\;\;\; &74\;\;\;\;\; &0100 \;1010\;\;\;\;\; &\text{J}\\ 11\;\;\;\;\; &0000\; 1011 \;\;\;\;\;&\text{VT}\;\;\;\;\;\;\;\;\;\; &75\;\;\;\;\; &0100\; 1011\;\;\;\;\; &\text{K}\\ 12\;\;\;\;\; &0000\; 1100 \;\;\;\;\;&\text{FF}\;\;\;\;\;\;\;\;\;\; &76\;\;\;\;\; &0100 \;1100\;\;\;\;\; &\text{L}\\ 13\;\;\;\;\; &0000\; 1101 \;\;\;\;\;&\text{CR}\;\;\;\;\;\;\;\;\;\; &77\;\;\;\;\; &0100\; 1101\;\;\;\;\; &\text{M}\\ 14\;\;\;\;\; &0000\; 1110 \;\;\;\;\;&\text{SO}\;\;\;\;\;\;\;\;\;\; &78\;\;\;\;\; &0100 \;1110\;\;\;\;\; &\text{N}\\ 15\;\;\;\;\; &0000\; 1111 \;\;\;\;\;&\text{SI}\;\;\;\;\;\;\;\;\;\; &79\;\;\;\;\; &0100\; 1111 \;\;\;\;\;&\text{O}\\ 16\;\;\;\;\; &0001\; 0000 \;\;\;\;\;&\text{DLE}\;\;\;\;\;\;\;\;\;\; &80\;\;\;\;\; &0101\; 0000 \;\;\;\;\;&\text{P}\\ 17\;\;\;\;\; &0001\; 0001 ;\;\;\;\;&\text{DC1}\;\;\;\;\;\;\;\;\;\; &81\;\;\;\;\; &0101\; 0001 \;\;\;\;\;&\text{Q}\\ 18\;\;\;\;\; &0001\; 0010 \;\;\;\;\;&\text{DC2}\;\;\;\;\;\;\;\;\;\; &82\;\;\;\;\; &0101\; 0010 \;\;\;\;\;&\text{R}\\ 19\;\;\;\;\; &0001\; 0011 \;\;\;\;\;&\text{DC3}\;\;\;\;\;\;\;\;\;\; &83\;\;\;\;\; &0101\; 0011 \;\;\;\;\;&\text{S}\\ 20\;\;\;\;\; &0001\; 0100 \;\;\;\;\;&\text{DC4}\;\;\;\;\;\;\;\;\;\; &84\;\;\;\;\; &0101\; 0100 \;\;\;\;\;&\text{T}\\ 21\;\;\;\;\; &0001\; 0101 \;\;\;\;\;&\text{NAK}\;\;\;\;\;\;\;\;\;\; &85\;\;\;\;\; &0101\; 0101 \;\;\;\;\;&\text{U}\\ 22\;\;\;\;\; &0001\; 0110 \;\;\;\;\;&\text{SYN}\;\;\;\;\;\;\;\;\;\; &86\;\;\;\;\; &0101\; 0110 \;\;\;\;\;&\text{V}\\ 23\;\;\;\;\; &0001\; 0111 \;\;\;\;\;&\text{ETB}\;\;\;\;\;\;\;\;\;\; &87\;\;\;\;\; &0101\; 0111 \;\;\;\;\;&\text{W}\\ 24\;\;\;\;\; &0001\; 1000 \;\;\;\;\;&\text{CAN}\;\;\;\;\;\;\;\;\;\; &88\;\;\;\;\; &0101\; 1000 \;\;\;\;\;&\text{X}\\ 25\;\;\;\;\; &0001\; 1001 \;\;\;\;\;&\text{EM}\;\;\;\;\;\;\;\;\;\; &89\;\;\;\;\; &0101 \;1001 \;\;\;\;\;&\text{Y}\\ 26\;\;\;\;\; &0001\; 1010 \;\;\;\;\;&\text{SUB}\;\;\;\;\;\;\;\;\;\; &90\;\;\;\;\; &0101\; 1010 \;\;\;\;\;&\text{Z}\\ 27\;\;\;\;\; &0001 \;1011 \;\;\;\;\;&\text{ESC}\;\;\;\;\;\;\;\;\;\; &91\;\;\;\;\; &0101\; 1011 \;\;\;\;\;&[\\ 28\;\;\;\;\; &0001 \;1100 \;\;\;\;\;&\text{FS}\;\;\;\;\;\;\;\;\;\; &92\;\;\;\;\; &0101\; 1100 \;\;\;\;\;&\setminus \\ 29\;\;\;\;\; &0001 \;1101 \;\;\;\;\;&\text{GS}\;\;\;\;\;\;\;\;\;\; &93\;\;\;\;\; &0101\; 1101 \;\;\;\;\;&]\\ 30\;\;\;\;\; &0001 \;1110 \;\;\;\;\;&\text{RS}\;\;\;\;\;\;\;\;\;\; &94\;\;\;\;\; &0101\; 1110 \;\;\;\;\;&\text{^} \\ 31\;\;\;\;\; &0001 \;1111 \;\;\;\;\;&\text{US}\;\;\;\;\;\;\;\;\;\; &95\;\;\;\;\; &0101 \;1111 \;\;\;\;\;&\underline{\;}\\ 32\;\;\;\;\; &0010 \;0000 \;\;\;\;\;&\text{}\;\;\;\;\;\;\;\;\;\; &96\;\;\;\;\; &0110 \;0000 \;\;\;\;\;&‘\\ 33\;\;\;\;\; &0010 \;0001 \;\;\;\;\;&!\;\;\;\;\;\;\;\;\;\; &97\;\;\;\;\; &0110 \;0001 \;\;\;\;\;&\text{a}\\ 34\;\;\;\;\; &0010 \;0010 \;\;\;\;\;&" \;\;\;\;\;\;\;\;\;\;&98\;\;\;\;\; &0110 \;0010 \;\;\;\;\;&\text{b}\\ 35\;\;\;\;\; &0010 \;0011 \;\;\;\;\;&\#\;\;\;\;\;\;\;\;\;\; &99\;\;\;\;\; &0110\; 0011 \;\;\;\;\;&\text{c}\\ 36\;\;\;\;\; &0010 \;0100 \;\;\;\;\;&$ \;\;\;\;\;\;\;\;\;\;&100\;\;\;\;\; &0110\; 0100 \;\;\;\;\;&\text{d}\\ 37\;\;\;\;\; &0010 \;0101 \;\;\;\;\;&\% \;\;\;\;\;\;\;\;\;\;&101\;\;\;\;\; &0110\; 0101 \;\;\;\;\;&\text{e}\\38\;\;\;\;\; &0010 \;0110 \;\;\;\;\;&\& \;\;\;\;\;\;\;\;\;\;&102\;\;\;\;\; &0110\; 0110 \;\;\;\;\;&\text{f}\\ 39\;\;\;\;\; &0010 \;0111 \;\;\;\;\;&’ \;\;\;\;\;\;\;\;\;\;&103\;\;\;\;\; &0110\; 0111 \;\;\;\;\;&\text{g}\\ 40\;\;\;\;\; &0010 \;1000 \;\;\;\;\;&( \;\;\;\;\;\;\;\;\;\;&104\;\;\;\;\; &0110\; 1000 \;\;\;\;\;&\text{h}\\ 41\;\;\;\;\; &0010 \;1001 \;\;\;\;\;&) \;\;\;\;\;\;\;\;\;\;&105\;\;\;\;\; &0110 \;1001 \;\;\;\;\;&\text{i}\\ 42\;\;\;\;\; &0010 \;1010 \;\;\;\;\;&* \;\;\;\;\;\;\;\;\;\;&106\;\;\;\;\;&0110 \;1010 \;\;\;\;\;&\text{j}\\ 43\;\;\;\;\; &0010 \;1011 \;\;\;\;\;&+ \;\;\;\;\;\;\;\;\;\;&107\;\;\;\;\; &0110 \;1011 \;\;\;\;\;&\text{k}\\ 44\;\;\;\;\; &0010 \;1100 \;\;\;\;\;&, \;\;\;\;\;\;\;\;\;\;&108\;\;\;\;\; &0110 \;1100 \;\;\;\;\;&\text{l}\\ 45\;\;\;\;\; &0010 \;1101 \;\;\;\;\;&- \;\;\;\;\;\;\;\;\;\;&109\;\;\;\;\; &0110 \;1101 \;\;\;\;\;&\text{m}\\ 46\;\;\;\;\; &0010 \;1110 \;\;\;\;\;&. \;\;\;\;\;\;\;\;\;\;&110\;\;\;\;\; &0110 \;1110 \;\;\;\;\;&\text{n}\\ 47\;\;\;\;\; &0010 \;1111 \;\;\;\;\;&/ \;\;\;\;\;\;\;\;\;\;&111\;\;\;\;\; &0110 \;1111 \;\;\;\;\;&\text{o}\\ 48\;\;\;\;\; &0011 \;0000 \;\;\;\;\;&0 \;\;\;\;\;\;\;\;\;\;&112\;\;\;\;\; &0111 \;0000 \;\;\;\;\;&\text{p}\\ 49\;\;\;\;\; &0011 \;0001 \;\;\;\;\;&1 \;\;\;\;\;\;\;\;\;\;&113\;\;\;\;\; &0111 \;0001 \;\;\;\;\;&\text{q}\\ 50\;\;\;\;\; &0011 \;0010 \;\;\;\;\;&2 \;\;\;\;\;\;\;\;\;\;&114\;\;\;\;\; &0111 \;0010 \;\;\;\;\;&\text{r}\\ 51\;\;\;\;\; &0011 \;0011 \;\;\;\;\;&3 \;\;\;\;\;\;\;\;\;\;&115\;\;\;\;\; &0111 \;0011 \;\;\;\;\;&\text{s}\\ 52\;\;\;\;\; &0011 \;0100 \;\;\;\;\;&4 \;\;\;\;\;\;\;\;\;\;&116\;\;\;\;\; &0111 \;0100 \;\;\;\;\;&\text{t}\\ 53\;\;\;\;\; &0011 \;0101 \;\;\;\;\;&5 \;\;\;\;\;\;\;\;\;\;&117\;\;\;\;\; &0111\; 0101 \;\;\;\;\;&\text{u}\\ 54\;\;\;\;\; &0011 \;0110 \;\;\;\;\;&6 \;\;\;\;\;\;\;\;\;\;&118\;\;\;\;\; &0111 \;0110 \;\;\;\;\;&\text{v}\\ 55\;\;\;\;\; &0011 \;0111 \;\;\;\;\;&7 \;\;\;\;\;\;\;\;\;\;&119\;\;\;\;\; &0111 \;0111 \;\;\;\;\;&\text{w}\\ 56\;\;\;\;\; &0011 \;1000 \;\;\;\;\;&8 \;\;\;\;\;\;\;\;\;\;&120\;\;\;\;\; &0111 \;1000 \;\;\;\;\;&\text{x}\\ 57\;\;\;\;\; &0011 \;1001 \;\;\;\;\;&9 \;\;\;\;\;\;\;\;\;\;&121\;\;\;\;\; &0111 \;1001 \;\;\;\;\;&\text{y}\\ 58\;\;\;\;\; &0011 \;1010 \;\;\;\;\;&: \;\;\;\;\;\;\;\;\;\;&122\;\;\;\;\; &0111 \;1010 \;\;\;\;\;&\text{z}\\ 59\;\;\;\;\; &0011 \;1011 \;\;\;\;\;&; \;\;\;\;\;\;\;\;\;\;&123\;\;\;\;\; &0111 \;1011 \;\;\;\;\;&\{ \\ 60\;\;\;\;\; &0011 \;1100 \;\;\;\;\;&< \;\;\;\;\;\;\;\;\;\;&124\;\;\;\;\; &0111 \;1100 \;\;\;\;\;&| \\ 61\;\;\;\;\; &0011 \;1101 \;\;\;\;\;&= \;\;\;\;\;\;\;\;\;\;&125\;\;\;\;\; &0111 \;1101 \;\;\;\;\;&\} \\ 62\;\;\;\;\; &0011 \;1110 \;\;\;\;\;&> \;\;\;\;\;\;\;\;\;\;&126\;\;\;\;\; &0111 \;1110 \;\;\;\;\;& \sim \\ 63\;\;\;\;\; &0011 \;1111 \;\;\;\;\;&? \;\;\;\;\;\;\;\;\;\;&127\;\;\;\;\; &0111 \;1111 \;\;\;\;\;&\text{DEL} \end{array} \)
Ahora solo se necesitan\(7\) bits para codificar los\(128\) posibles valores en el sistema ASCII, lo que puede verificarse fácilmente al notar que los bits más a la izquierda en todas las representaciones binarias anteriores son\(0\). La mayoría de las computadoras usan palabras de\(8\) bits o “bytes” como sus unidades básicas de información, y el hecho de que el código ASCII solo requiera\(7\) bits lleva a alguien a pensar en un uso para ese bit adicional. Se convirtió en un “bit de verificación de paridad”. Si los siete bits de una codificación ASCII tienen un número impar de\(1\)'s, el bit de verificación de paridad se establece en\(1\); de lo contrario, se establece en\(0\). El resultado de esto es que, posteriormente, todas las palabras de\(8\) bit que codifican datos ASCII tendrán un número par de\(1\)'s Este es un ejemplo de un llamado código de detección de errores conocido como el “código par” o el “código de verificación de paridad”. Si los datos se envían a través de un canal de telecomunicaciones ruidoso, o se almacenan en una memoria de computadora falible, hay una probabilidad pequeña pero calculable de que habrá un “error de bit”. Por ejemplo, una computadora podría enviar\(10000111\) (que es el código ASCII que dice “sonar la campana”) pero otra máquina a través de la red podría recibir\(10100111\) (el\(3^{\text{rd}}\) bit de la izquierda se ha recibido por error) ahora si solo estamos mirando los siete bits más a la derecha pensaremos que el Se ha recibido código ASCII para una sola cotización, pero si observamos que este dato recibido tiene un número impar de unos nos daremos cuenta de que algo anda mal. Hay otros esquemas de codificación más avanzados que nos permitirán no solo detectar un error, ¡sino (dentro de los límites) corregirlo también! Esta hazaña bastante asombrosa es lo que hace que la telefonía inalámbrica (sin mencionar las comunicaciones con sondas de espacio profundo, ¡gritos! Lo mencioné) trabajo.
El concepto de paridad se puede utilizar en muchos escenarios para demostrar algunos resultados bastante notables.
En la Sección 6.3, presentamos la idea de una gráfica. Esta noción fue utilizada por primera vez por Leonhard Euler para resolver un problema matemático recreativo planteado por los ciudadanos de Königsberg, Prusia (esta es la ciudad ahora conocida como Kaliningrado, Rusia). Königsberg estaba situado en un lugar donde se juntan dos ramas del río Pregel 2; también hay una gran isla situada cerca de esta confluencia. Para la época de Euler, la ciudad de Königsberg cubría esta isla así como las orillas norte y sur del río y también el promontorio donde se juntaban las ramas. Se había construido una red de siete puentes para conectar todas estas masas de tierra. Se alega que los habitantes del pueblo quedaron cautivados por la cuestión de si era posible salir de su casa y dar un paseo por la ciudad que cruzó cada uno de los puentes exactamente una vez y, finalmente, regresar a su casa.
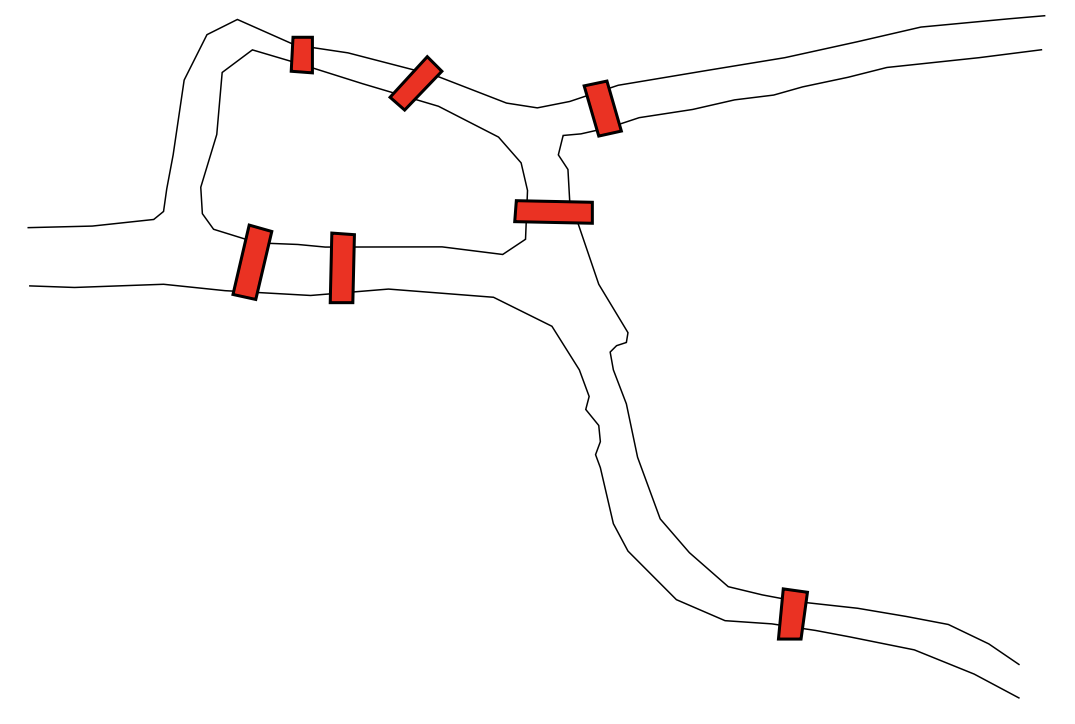
Euler resolvió la pregunta (no se puede hacer) de convertir el mapa de Königsberg en una gráfica y luego hacer algunas observaciones simples sobre las paridades de los nodos en esta gráfica. El grado de un nodo en una gráfica es el número de bordes que inciden con él (si está presente un llamado “borde de bucle”, agrega dos al grado del nodo). La “paridad de un nodo” es la taquigrafía de la “paridad del grado del nodo”.
La gráfica de Königsberg tiene\(4\) nodos: uno de grado\(5\) y tres de grado\(3\). Todos los nodos son impares. ¿Sería posible modificar Königsberg o llegar a una gráfica completamente nueva que tenga algunos nodos pares? Bueno, la respuesta a eso es fácil — simplemente derribar uno de los puentes, y dos de los nodos tendrán su grado cambiado en uno; ambos se volverán parejos. Observe que, al eliminar un borde, efectuamos la paridad de dos nodos. ¿Es posible crear una gráfica con cuatro nodos en los que solo uno de ellos esté parejo? De manera más general, dada alguna lista corta de números naturales, ¿es posible dibujar una gráfica cuyos grados son los números listados?
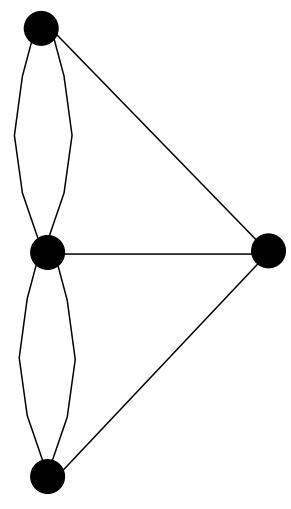
Intente dibujar gráficas que tengan las siguientes listas de grados de vértice. (En algunos casos será imposible.)
- \(\{1, 1, 2, 3, 3\}\)
- \(\{1, 2, 3, 5\}\)
- \(\{1, 2, 3, 4\}\)
- \(\{4, 4, 4, 4, 5\}\)
- \(\{3, 3, 3, 3\}\)
- \(\{3, 3, 3, 3, 3\}\)
Cuando es posible crear una gráfica con una lista especificada de grados de vértice, suele ser fácil de hacer. Por supuesto, cuando es imposible luchas un poco. Para ayudar a que las cosas rueden (por si acaso no has hecho realmente el ejercicio) voy a dar una pista — para la primera lista es posible dibujar una gráfica, para la segunda no lo es. ¿Se puede distinguir el patrón? ¿Qué hace razonable una lista de grados de vértice y otra no?
(Si no hiciste el último ejercicio, deja de ser tan cojo y pruébalo ya. Por cierto, si lo hiciste, ¡bien por ti! Puedes unirte a mí ahora para burlarte de todas esas personas que están corriendo hacia atrás para hacer la última, o probar lo siguiente:)
Determinar una manera de distinguir una secuencia de números que puede ser la secuencia de grados de alguna gráfica de las secuencias que no pueden ser.
Bien, ahora si estás leyendo esta oración deberías saber que cualquier otra lista de grados de vértice arriba es imposible, deberías tener gráficas dibujadas en el margen aquí para las secuencias de\(1^{\text{st}}\),\(3^{\text{rd}}\) y\(5^{\text{th}}\) grados, y es posible que hayas descubierto alguna versión de lo siguiente
En una gráfica no dirigida, el número de vértices que tienen un grado impar es par.
Una declaración un poco más compasiva es: Todas las gráficas tienen un número par de nodos impares.
Dejaremos la prueba de este teorema a los ejercicios pero la mayor parte del trabajo se realiza en probar el siguiente resultado equivalente.
En una gráfica no dirigida, la suma de los grados de los vértices es pareja.
- Prueba
-
La suma de los grados de todos los vértices en una gráfica\(G\),
\[\sum_{v∈V (G)} \text{deg}(v),\]
cuenta cada borde de\(G\) exactamente dos veces.
Por lo tanto,
\[\sum_{v∈V (G)} \text{deg}(v) = 2 · |E(G)|.\]
En particular vemos que esta suma es parejo.
Q.E.D.
La cuestión de si puede existir una gráfica que tenga una lista dada de grados de vértice se reduce a un pequeño argumento elegante utilizando ambas técnicas del título de esta sección. Contamos el conjunto de bordes de la gráfica de dos maneras —una vez de la manera habitual y otra sumando los grados de vértice; también observamos que dado que este último recuento es en realidad un doble conteo podemos traer en el concepto de paridad.
Otro argumento perfectamente encantador que involucra la paridad surge en las preguntas sobre si es posible o no tejear un tablero de ajedrez podado con dominó. Hemos visto dominó antes en la Sección 5.1 y solo estamos esperando que te hayas topado con tableros de ajedrez antes. Por lo general, un tablero de ajedrez lo es\(8 × 8\), pero nos gustaría adoptar una interpretación más liberal de que un tablero de ajedrez puede ser cualquier cuadrícula rectangular de cuadrados que podamos elegir. 3 Supongamos que tenemos un suministro de dominó que son del tamaño justo que si se colocan sobre un tablero de ajedrez cubren perfectamente dos cuadrados adyacentes. Nuestra primera pregunta es bastante simple. ¿Es posible tejear perfectamente un\(m × n\) tablero de ajedrez con ese tipo de dominó?
Primero, especifiquemos un poco más la pregunta. Por “perfectamente alicatado” un tablero de ajedrez queremos decir que cada dominó yace (completamente) en el tablero, cubriendo precisamente dos cuadrados, y que cada cuadrado del tablero está cubierto por un dominó.
La respuesta es sencilla. Si al menos uno de m o n es par se puede hacer. Una condición necesaria es que el número de plazas sea par (ya que cada dominó cubre dos casillas) y así, si ambas\(m\) y\(n\) son impares nos quedaremos sin suerte.
Una “tabla podada” se obtiene ya sea eliminando literalmente algunos de los cuadrados o tal vez marcándolos como fuera de los límites de alguna manera. Cuando hacemos preguntas sobre los inclinados perfectos de los tableros de ajedrez podados las cosas se vuelven más interesantes y la noción de paridad se puede utilizar de varias maneras.
Aquí hay dos problemas de mosaico con respecto a los tableros de ajedrez cuadrados:
- Una tabla cuadrada de lados pares (por ejemplo, una\(8 × 8\) tabla ordinaria) con esquinas diagonalmente opuestas podadas.
- Una tabla de lados impares con un cuadrado podado.
Ambas situaciones satisfacen la condición básica necesaria de que el número de plazas en el tablero debe ser parejo. Es posible que pueda determinar otro enfoque de “paridad” para estos problemas de ordenamiento en mosaico intentando lo siguiente
A continuación se muestran dos tableros de ajedrez de cinco por cinco cada uno con un solo cuadrado podado. Uno puede ser alicatado por dominó y el otro no. ¿Cuál es cuál?
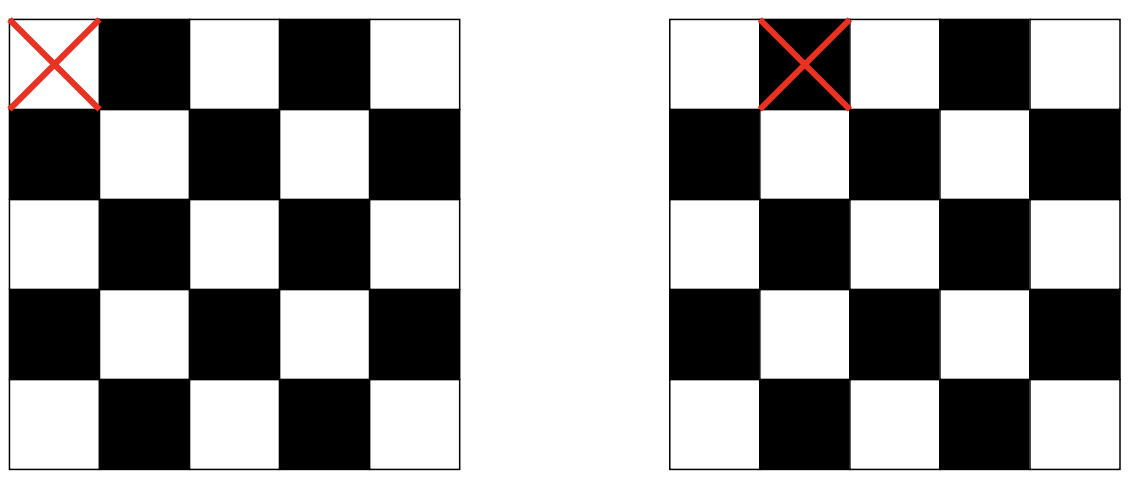
El patrón de cuadrados blancos y negros en un tablero de ajedrez es un ejemplo de una especie de paridad artificial, si numeramos los cuadrados del tablero apropiadamente entonces los cuadrados impares serán blancos y los cuadrados pares serán negros. Estamos acostumbrados a que los tableros de ajedrez tengan este patrón alternante negro/blanco en ellos, pero nada de estos problemas de mosaico requirió esa estructura 4. Si estuviéramos acostumbrados a los tableros de ajedrez monocromáticos, tal vez nunca resolviéramos los dos problemas anteriores, a menos que, por supuesto, inventáramos el esquema de coloración para resolverlos. Un tablero de ajedrez impar por impar tiene más cuadrados de un color que del otro. Un tablero de ajedrez impar por impar necesita tener un cuadrado podado para que sea posible que sea alicatado con fichas de dominó, pero si se poda el cuadrado de color incorrecto, seguirá siendo imposible. Cada dominó cubre dos cuadrados, ¡uno de cada color! (Por lo que la tabla podada debe tener el mismo número de cuadrados blancos que el negro).
Cerraremos esta sección con otro ejemplo de la técnica de contar de dos maneras.
Un cuadrado mágico de orden\(n\) es una\(n×n\) matriz cuadrada que contiene los números\(1, 2, 3, . . . , n^2\). Los números deben estar dispuestos de tal manera que cada fila y cada columna sumen al mismo número — este valor se conoce como la suma mágica.
Por ejemplo, el siguiente es un cuadrado\(3\) mágico de orden.
| \(1\) | \(6\) | \(8\) |
| \(5\) | \(7\) | \(3\) |
| \(9\) | \(2\) | \(4\) |
La definición de un cuadrado mágico requiere que las filas y columnas sumen al mismo número pero no dice nada sobre lo que debe ser ese número. Es concebible que pudiéramos producir cuadrados mágicos (del mismo orden) teniendo diferentes sumas mágicas. Esto es concebible, pero de hecho la suma mágica está determinada completamente por\(n\).
Un cuadrado mágico de orden\(n\) tiene una suma mágica igual a\(\dfrac{n^3 + n}{2}\).
- Prueba
-
Contamos el total de las entradas en la plaza mágica de dos maneras. La suma de todas las entradas en el cuadrado mágico es
\[S = 1 + 2 + 3 + . . . + n^2.\]
Usando la fórmula para la suma de los primeros\(k\) naturales\(( \sum^{k}_{i=1} i = \dfrac{k^2+k}{2} )\) y evaluando en\(n^2\) da
\[S = \dfrac{n^4 + n^2}{2}.\]
Por otro lado, si la suma mágica es\(M\), entonces cada una de las\(n\) filas tiene números en ella que se suman a\(M\) así
\[S = nM.\]
Al igualar estas diferentes expresiones\(S\) y resolver para\(M\), demostramos el resultado deseado:
\[nM = \dfrac{n^4 + n^2}{2},\]
por lo tanto
\[M = \dfrac{n^3 + n}{2} .\]
Q.E.D.
Ejercicios:
Un recorrido a pie por K¨onigsberg como el que se describe en esta sección, o más generalmente, un circuito a través de una gráfica arbitraria que cruza cada borde precisamente una vez y comienza y termina en el mismo nodo se conoce como circuito euleriano. Un camino euleriano también cruza cada borde de una gráfica exactamente una vez pero comienza y termina en distintos nodos. Para cada una de las siguientes gráficas determinar si es posible un circuito o trayectoria euleriana, y de ser así, dibujarla.
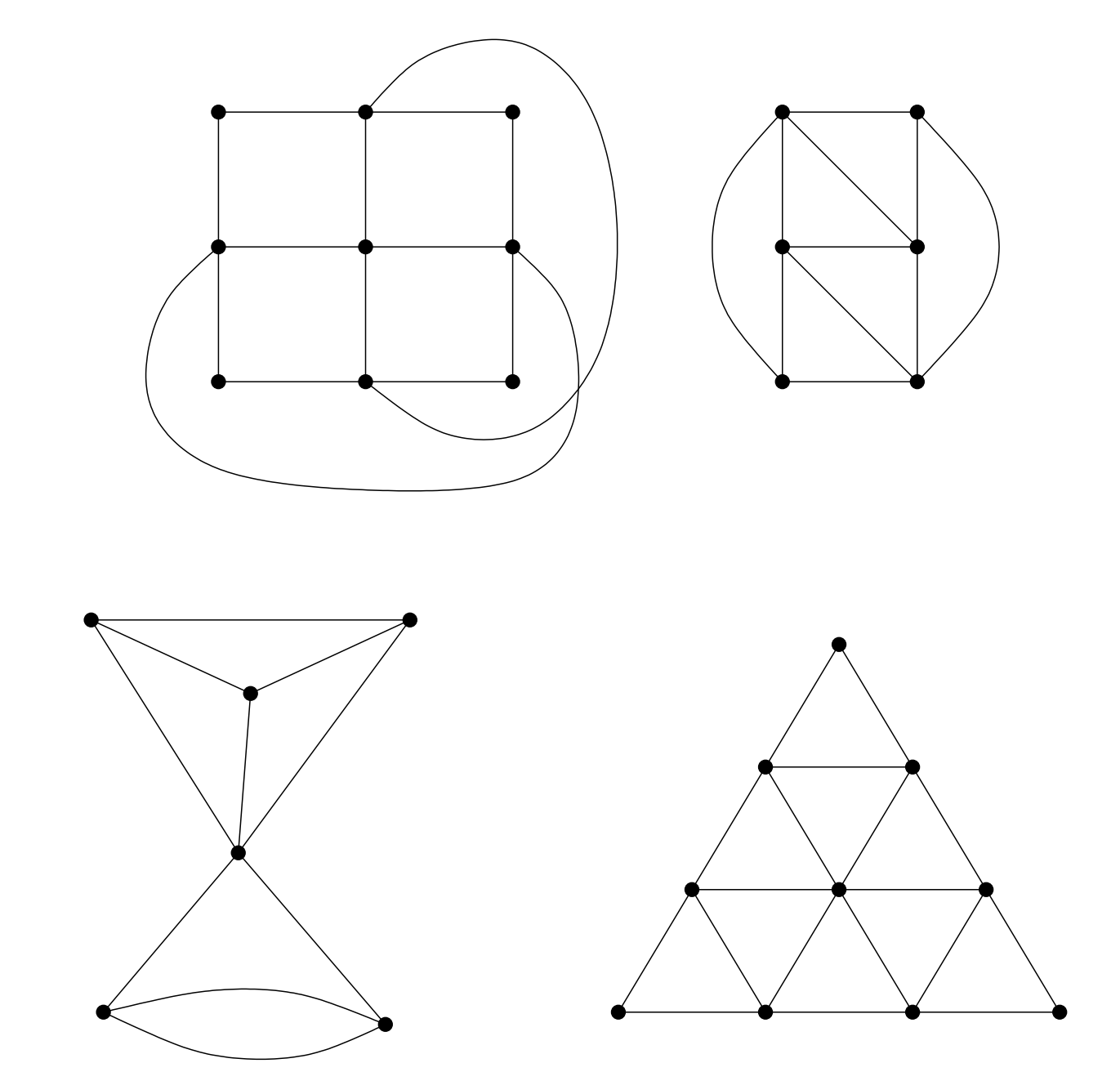
Completa la prueba del hecho de que “Cada gráfica tiene un número par de nodos impares”.
Proporcionar un argumento sobre por qué un\(8 × 8\) tablero de ajedrez con dos cuadrados podados de esquinas diagonalmente opuestas no se puede enmarcar con fichas de dominó.
Demostrar que, si\(n\) es extraño, cualquier\(n × n\) tablero de ajedrez con un cuadrado del mismo color que una de sus esquinas podadas puede ser alicatado por dominó.
Los cinco tetrominos (familiares para los jugadores del videojuego Tetris) son familiares de dominó conformados por cuatro cuadraditos pequeños.
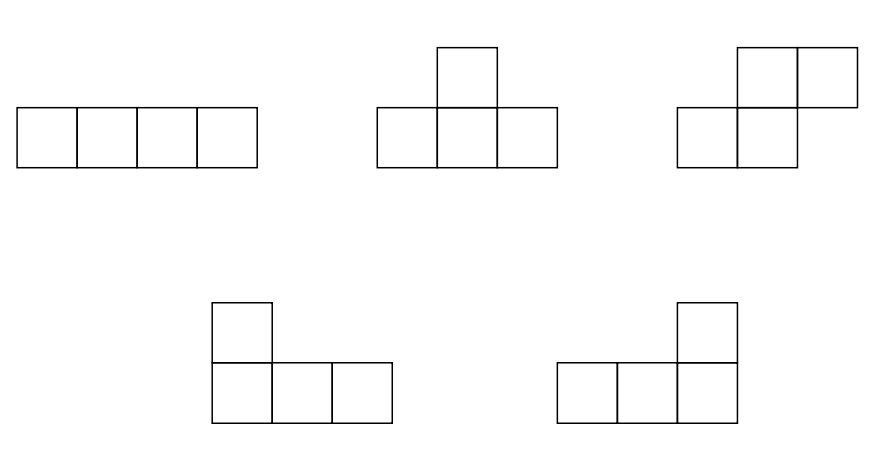
Todos juntos estos cinco tetrominos contienen\(20\) cuadrados por lo que es concebible que puedan ser utilizados para tejar un\(4 ×5\) tablero de ajedrez. Demostrar que esto en realidad es imposible.
Estado condiciones necesarias y suficientes para la existencia de un circuito euleriano en una gráfica.
Estado condiciones necesarias y suficientes para la existencia de un camino euleriano en una gráfica.
Construir cuadrados mágicos de orden\(4\) y\(5\).
Un hexágono mágico de orden\(2\) consistiría en rellenar los números de\(1\) a\(7\) en la matriz hexagonal de abajo. La condición mágica significa que cada una de las\(9\) “líneas” de hexágonos adyacentes tendría la misma suma. ¿Esto es posible?
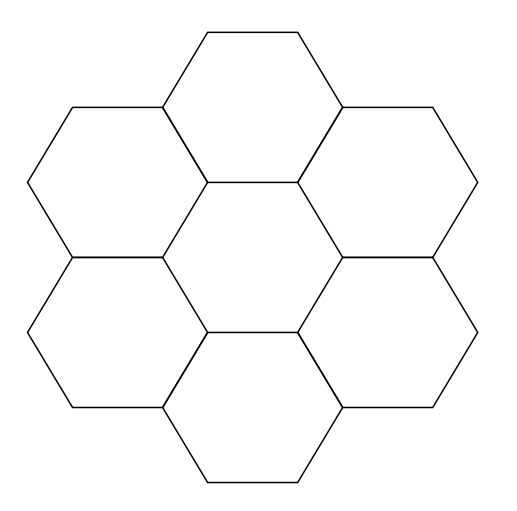
¿Hay un hexágono mágico de orden\(3\)?


