9.1: Milagro de Morley
- Page ID
- 114033
Probablemente hayas oído hablar de la imposibilidad de trisectar un ángulo. (Agárrate para una diatriba rápida sobre la importancia de entender tus hipótesis) Lo que realmente es cierto es que no puedes trisecar un ángulo genérico si aceptas la restricción de usar las herramientas anticuadas de la geometría euclidiana: la brújula y el borde recto. Hay muchas construcciones que no se pueden hacer usando solo una trisección de borde recto y brújula, duplicación de un cubo 1, cuadratura de un círculo, construcción de un heptágono regular, etcétera.
Si te permites usar una regla, es decir, un borde recto con marcas en ella (de hecho, realmente solo necesitas dos marcas a una distancia unitaria) entonces la trisección angular se realiza a través de lo que se conoce como construcción de neusis. Sin embargo, debido al lugar central de los Elementos de Euclides en la formación matemática a lo largo de los siglos, y con ello, una predilección muy fuerte hacia lo que es posible a través de la brújula y la recta solo, tal vez no sea sorprendente que un resultado perfectamente hermoso que involucró ángulos trisectantes no fueron descubiertos hasta\(1899\), cuando Frank Morley declaró su Teorema del Trisector. Hay mucho más en este resultado de lo que vamos a decir aquí —tanto más que el nombre “Milagro de Morley” que se le ha dado al teorema del Trisector está verdaderamente justificado— ¡pero incluso la parte simple e inicial de esta bella teoría es posiblemente milagrosa! Para conocer más sobre el teorema de Morley y su extensión ver [8].
Entonces, ¡digamos el teorema!
Comienza con un triángulo arbitrario\({\triangle}ABC\). Trisecta cada uno de sus ángulos para obtener un diagrama algo así en la Figura\(9.1.1\).
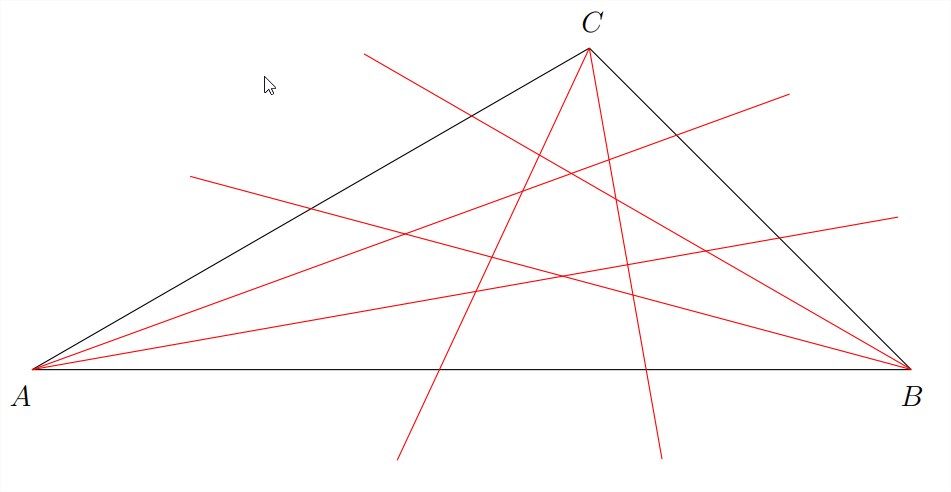
Los seis trisectores angulares que acabamos de dibujar se cruzan entre sí en bastantes puntos.
Literalmente podrías contar el número de puntos de intersección entre los trisectores angulares en el diagrama, pero también deberías poder contarlos (quizás deberíamos decir “doblemente contarlos”) combinatoriamente. ¡Pruébalo!
Entre los puntos de intersección de los trisectores angulares hay tres que destacaremos: las intersecciones de trisectores adyacentes. En Figura se indica\(9.1.2\) la intersección de trisectores adyacentes, adicionalmente, los hemos conectado entre sí para formar un pequeño triángulo en el centro de nuestro triángulo original.
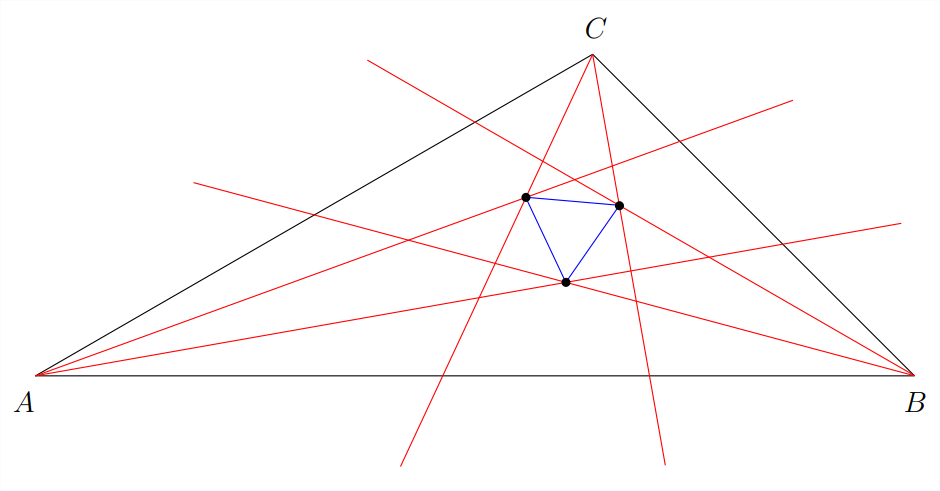
¿Estás listo para la parte milagrosa? Bien, ¡aquí va!
Los puntos de intersección de los trisectores adyacentes en un triángulo arbitrario\(\triangle ABC\) forman los vértices de un triángulo equilátero.
En otras palabras, ese pequeño triángulo azul en la Figura\(9.1.2\) que algo así como podría ser equilátero en realidad tiene los tres lados iguales entre sí. Además, no importa con qué triángulo empecemos, si hacemos la construcción anterior ¡obtendremos un\(60^\circ - 60^\circ - 60^\circ\) triángulo perfecto en el medio!
Las fuentes difieren, pero no está claro si Morley alguna vez demostró su teorema. La primera prueba válida (según R. K. Guy en [8] fue publicada en\(1909\) por M. Satyanarayana [15]. Ahora hay otras pruebas conocidas, por ejemplo el sitio web de cortar el nudo (http://www.cut-the-knot.org/) expone no menos de nueve pruebas diferentes. La prueba de Satyanarayana utilizó trigonometría. La prueba que veremos aquí es posiblemente la más corta jamás producida y se debe a John Conway. ¡Definitivamente es una “prueba de libro”!
Supongamos que\(\triangle ABC\) se da un triángulo arbitrario. Queremos mostrar que el triángulo cuyos vértices son las intersecciones de los trisectores adyacentes es equilátero, este triángulo se denominará triángulo de Morley. Vamos a denotar también por\(A\),\(B\) y\(C\) las medidas de los ángulos de\(\triangle ABC\). (Esto es lo que generalmente se conoce como un “abuso de notación” — estamos confundiendo intencionalmente los vértices (\(A\),\(B\) y\(C\)) del triángulo con la medida de los ángulos en esos vértices.) Resulta que es bastante difícil razonar a partir de nuestro conocimiento de cuáles son los ángulos\(A\),\(B\) y\(C\) son deducir que el triángulo Morley es equilátero. Cómo suena el siguiente plan: supongamos que construimos un triángulo, que definitivamente sí tiene un triángulo equilátero de Morley, cuyos ángulos también resultan ser\(A\),\(B\) y\(C\). Tal triángulo sería similar 2 al triángulo original\(\triangle ABC\) —si seguimos la similitud transformamos desde el triángulo construido de nuevo a\(\triangle ABC\) veremos que sus triángulos Morley deben coincidir; así si uno es equilátero también lo es el otro!
Una de las características de la prueba de Conway que lleva a su gran sucinta y belleza es su introducción de alguna notación muy agradable. Ya que estamos tratando con trisectores angulares, vamos\(a\),\(b\) y\(c\) ser ángulos tales que\(3a = A\),\(3b = B\) y\(3c = C\). Además, deja que una estrella superíndice denote el ángulo que es\(\dfrac{π}{3}\) (o\(60^{\circ}\) si lo prefieres) mayor que un ángulo dado. Entonces, por ejemplo,
\[ a^{\star}= a + \dfrac{\pi}{3} \]
y
\[ a^{\star\star} = a + \dfrac{2}{3}. \]
Ahora bien, fíjense que la suma\(a+b+c\) debe ser\(\dfrac{\pi}{3}\). Esto es una consecuencia inmediata de\(A+B+C=\pi\) lo cual es cierto para cualquier triángulo en el plano. De ello se deduce que distribuyendo dos estrellas entre los tres números\(a\),\(b\) y\(c\) vamos a llegar a tres cantidades que suman a\(\pi\). Es decir, hay triángulos euclidianos que tienen los siguientes triples como sus ángulos de vértice:
\((a, b, c^{\star\star}) \;\;\;\;\;\;\;\;(a, b^{\star} , c^{\star} ) \\ (a, b^{\star\star}, c) \;\;\;\;\;\;\;\;(a^{\star} , b^{\star} , c) \\ (a^{\star\star}, b, c) \;\;\;\;\;\;\;\;(a^{\star}, b, c^{\star} )\)
En pocas palabras, la prueba de Conway consiste en comenzar con un triángulo equilátero de longitud lateral unitaria, agregar versiones apropiadamente escaladas de los seis triángulos anteriores y terminar con una figura (que tiene un triángulo Morley equilátero) similar a\({\triangle}ABC\). La imagen genérica se da en la Figura\(9.1.3\). Antes de que podamos realmente contar este argumento como prueba, necesitamos decir un poco más sobre lo que significa la frase “apropiadamente escalado”. Para escalar apropiadamente los triángulos (los pequeños agudos) que aparecen verdes en la Figura\(9.1.3\) tenemos un trabajo relativamente fácil — simplemente escalarlos para que el lado opuesto al ángulo trisectado tenga la longitud uno; de esa manera se unirán perfectamente con el triángulo equilátero central.
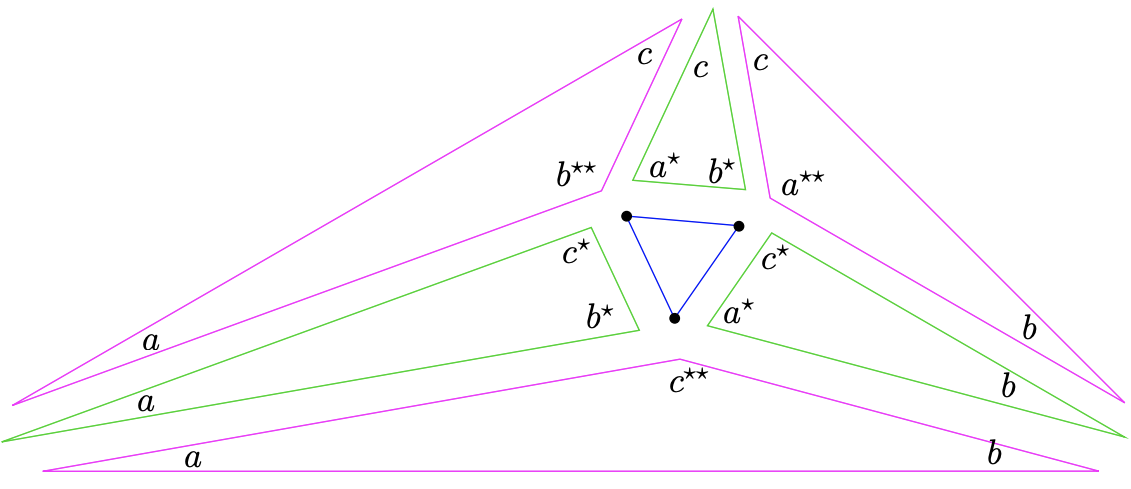
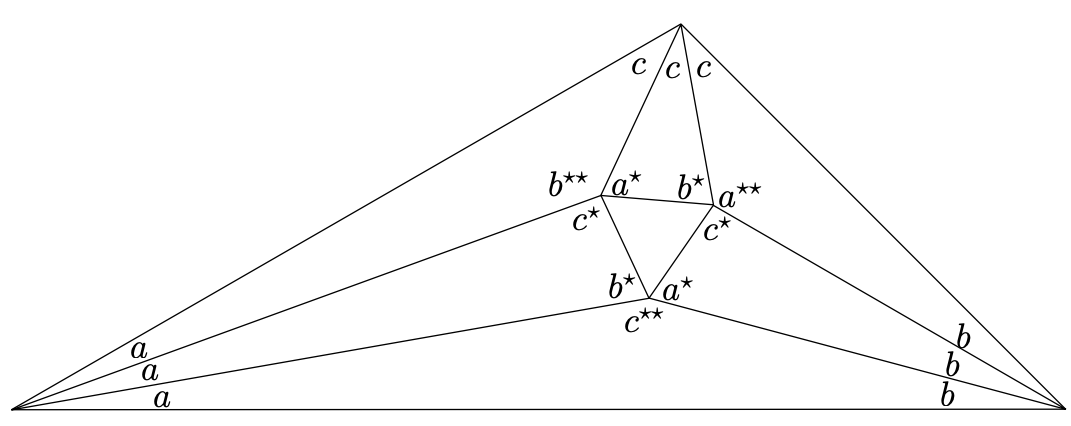
Los triángulos (estos son los obtusos más grandes) que aparecen morados en la Figura\(9.1.3\) son un poco más desconcertantes. Aparentemente, tenemos dos trabajos diferentes que cumplir: debemos escalarlos para que ambos bordes que compartirán con triángulos verdes tengan las longitudes correctas. ¿Cómo sabemos que esto no requerirá dos factores de escalado diferentes? Conway también desarrolló un argumento elegante que maneja esta pregunta también. Considera el triángulo púrpura en la parte inferior del diagrama en la Figura\(9.1.3\) — tiene ángulos de vértice\((a,b,c^{\star\star})\). Es posible construir triángulos similares (vía reflejos) a los triángulos verdes adyacentes\((a, b^\star, c^\star)\) y\((a^\star, b, c^\star)\) de triángulo\((a,b,c^{\star\star})\). Para ello basta con construir dos líneas que atraviesan el vértice superior (donde\(c^{\star\star}\) está el ángulo) que cortan el borde opuesto en el ángulo\(c^\star\) en los dos sentidos posibles — estas dos líneas coincidirán si sucediera eso\(c^\star\) es precisamente \(\dfrac{\pi}{2}\)pero generalmente habrá dos y es evidente que los dos segmentos lineales formados tienen la misma longitud. Escalamos el triángulo púrpura para que esta longitud común sea\(1\). Ver Figura\(9.1.4\).
Si ocurriera eso\(c^{\star} = \dfrac{π}{2}\), ¿qué podemos decir\(C\)?

Por supuesto, los otros dos triángulos obtusos pueden manejarse de manera similar.
Ejercicios:
¿Qué valor debemos obtener si sumamos todos los ángulos que aparecen alrededor de uno de los vértices interiores en el diagrama terminado? Verifica que los tres tengan la suma correcta.
En esta sección, hablamos de similitud. Dos figuras en el plano son similares si es posible convertir una en la otra mediante una secuencia de mapeos: una traslación, una rotación y una escala.
La similitud geométrica es una relación de equivalencia. Para fijar nuestra notación, vamos a\(T(x, y)\) representar una traducción genérica,\(R(x, y)\) una rotación y\(S(x, y)\) una escala — así una similitud genérica es una función de\(\mathbb{R}^2\) a\(\mathbb{R}^2\) que se puede escribir en la forma\(S(R(T(x, y)))\).
Discutir las tres propiedades de una relación de equivalencia (reflexividad, simetría y transitividad) en términos de similitud geométrica.


