9.2: Cinco pasos hacia el vacío
- Page ID
- 114032
En esta sección hablaremos de otra Prueba de libro también debido a John Conway. Esta prueba sirve como introducción a una técnica general realmente poderosa: la idea de un invariante. Una invariante es algún tipo de cantidad que se puede calcular que por sí misma no cambia a medida que se cambian otras cosas. Por supuesto que diferentes situaciones tienen diferentes cantidades invariantes.
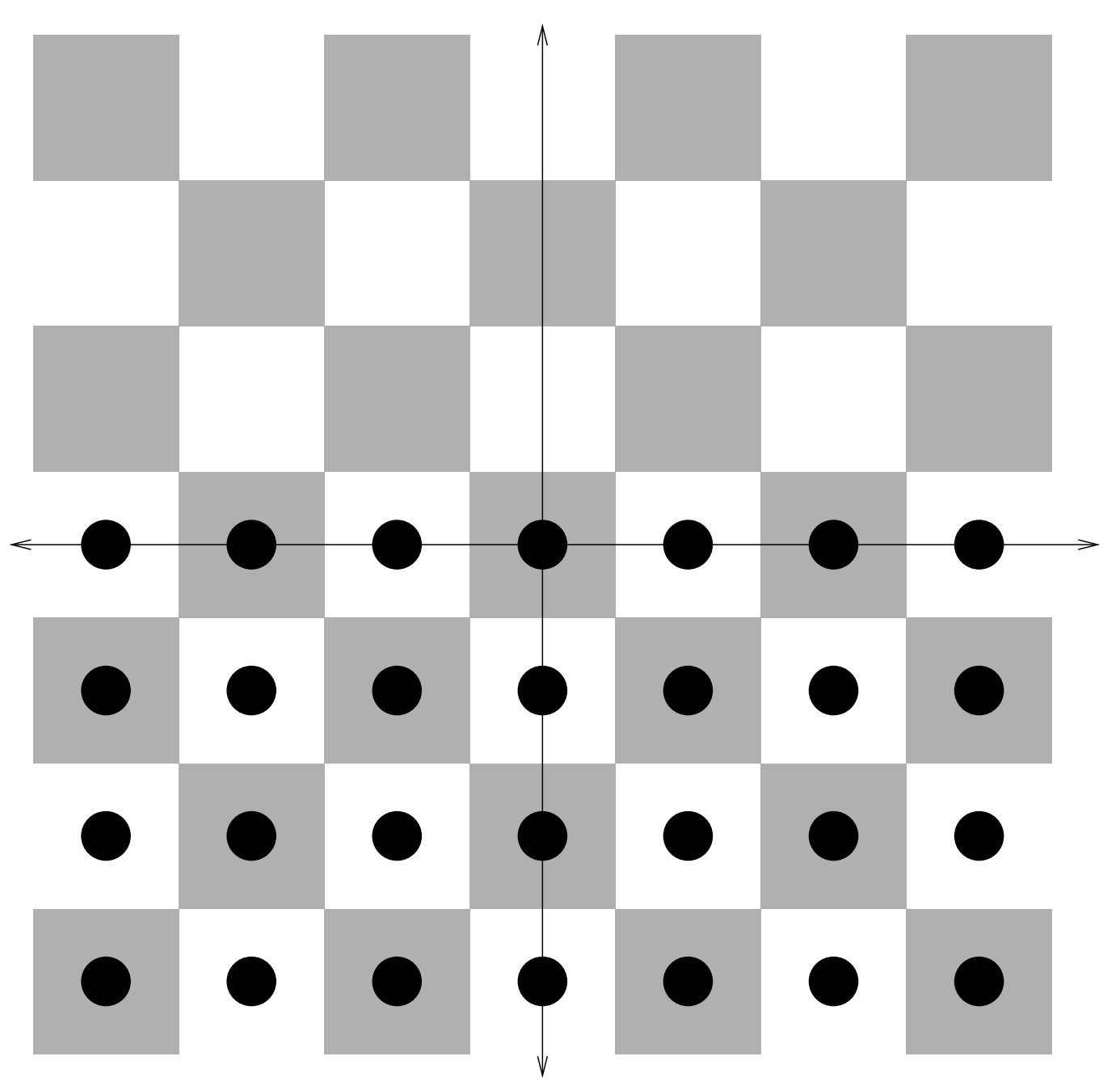
La configuración aquí es simple y relativamente intuitiva. Tenemos un montón de damas en un tablero de ajedrez — de hecho tenemos un número infinito de damas, pero no llenando todo el tablero, llenan completamente un medio plano infinito que podríamos tomar para ser el conjunto
\[ S = \{(x, y) x ∈ \mathbb{Z} ∧ y ∈ \mathbb{Z} ∧ y ≤ 0\}. \]
Ver Figura\(9.2.1\).
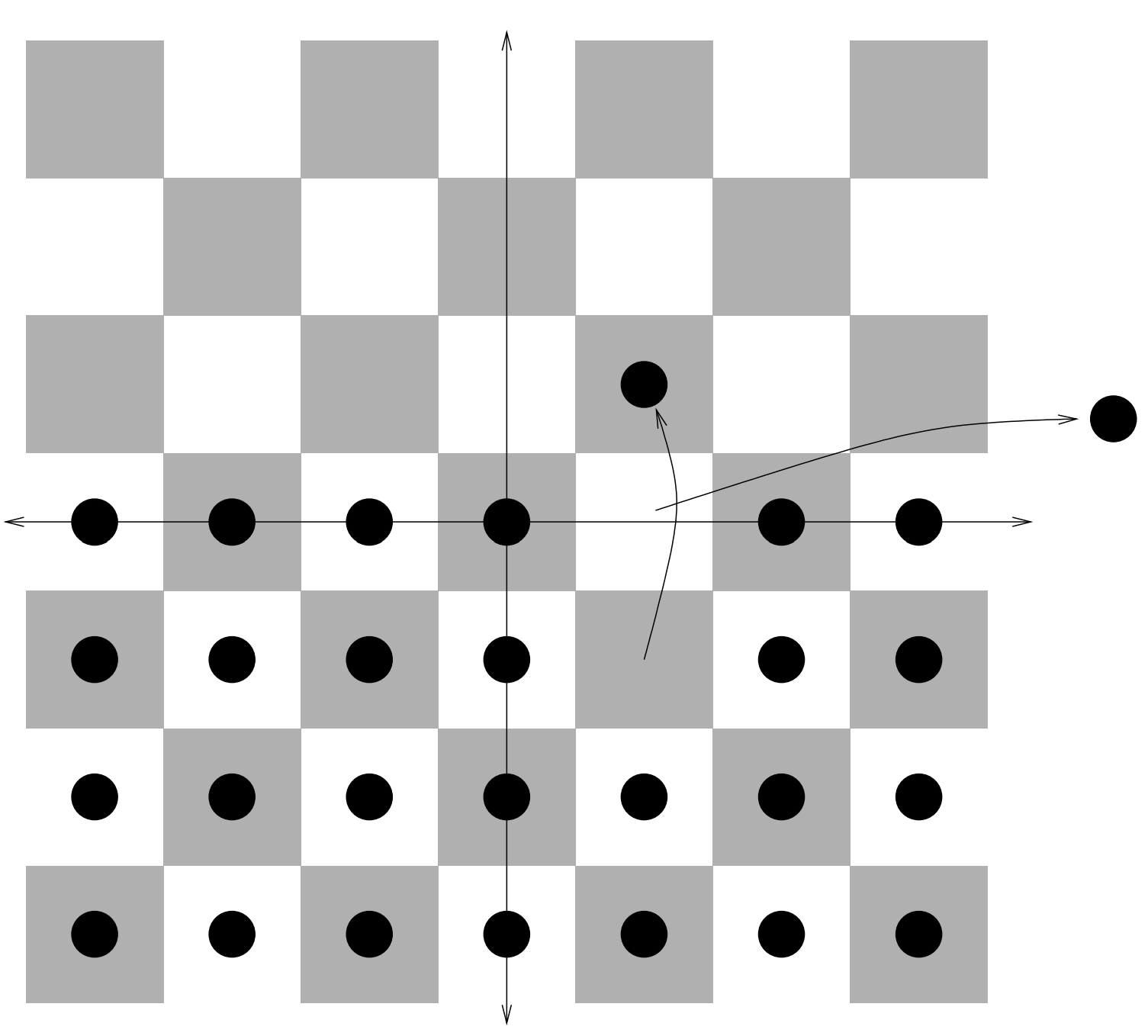
Piensa en estas damas como un ejército y el medio plano superior es “territorio enemigo”. Nuestro objetivo es trasladar a uno de nuestros soldados al territorio enemigo en la medida de lo posible. El problema es que nuestros “soldados” se mueven como lo hacen las damas, saltando sobre otro hombre (que luego es retirado del tablero). Está claro que podemos meter a alguien en territorio enemigo — simplemente tomar a alguien en la segunda fila y saltar a un tipo en la primera fila. También es bastante fácil ver que es posible meter a un hombre dos pasos en territorio enemigo —podríamos traer a dos hombres adyacentes un solo paso a territorio enemigo, hacer que uno de ellos salte al otro y luego un hombre del rango delantero pueda saltar sobre él.
En la estrategia que acabamos de enunciar se utiliza a\(4\) los hombres (en el sentido de que son retirados del tablero\(5\) —si se cuenta el que acaba de subir dos escalones en territorio enemigo también). Encuentra una estrategia para mover a alguien dos pasos hacia territorio enemigo que sea más eficiente —es decir, implica menos saltos.
Determinar la forma más eficiente de meter a un hombre tres pasos en territorio enemigo. Un tablero de damas real y piezas (o algunas monedas, o rocas) pueden ser útiles.
Vamos a contar al hombre que termina por cierto número de pasos por encima del\(x\) eje -eje, así como todas las piezas que se saltan y se sacan del tablero como medida de la eficiencia de una estrategia. Si hiciste el último ejercicio correctamente deberías haber encontrado que ocho hombres son el mínimo requerido para\(3\) entrar en territorio enemigo. Hasta el momento, el número de hombres requeridos para llegar una distancia dada a territorio enemigo parece ser siempre un poder de\(2\).
| # de pasos | # de hombres |
| \(1\) | \(2\) |
| \(2\) | \(4\) |
| \(3\) | \(8\) |
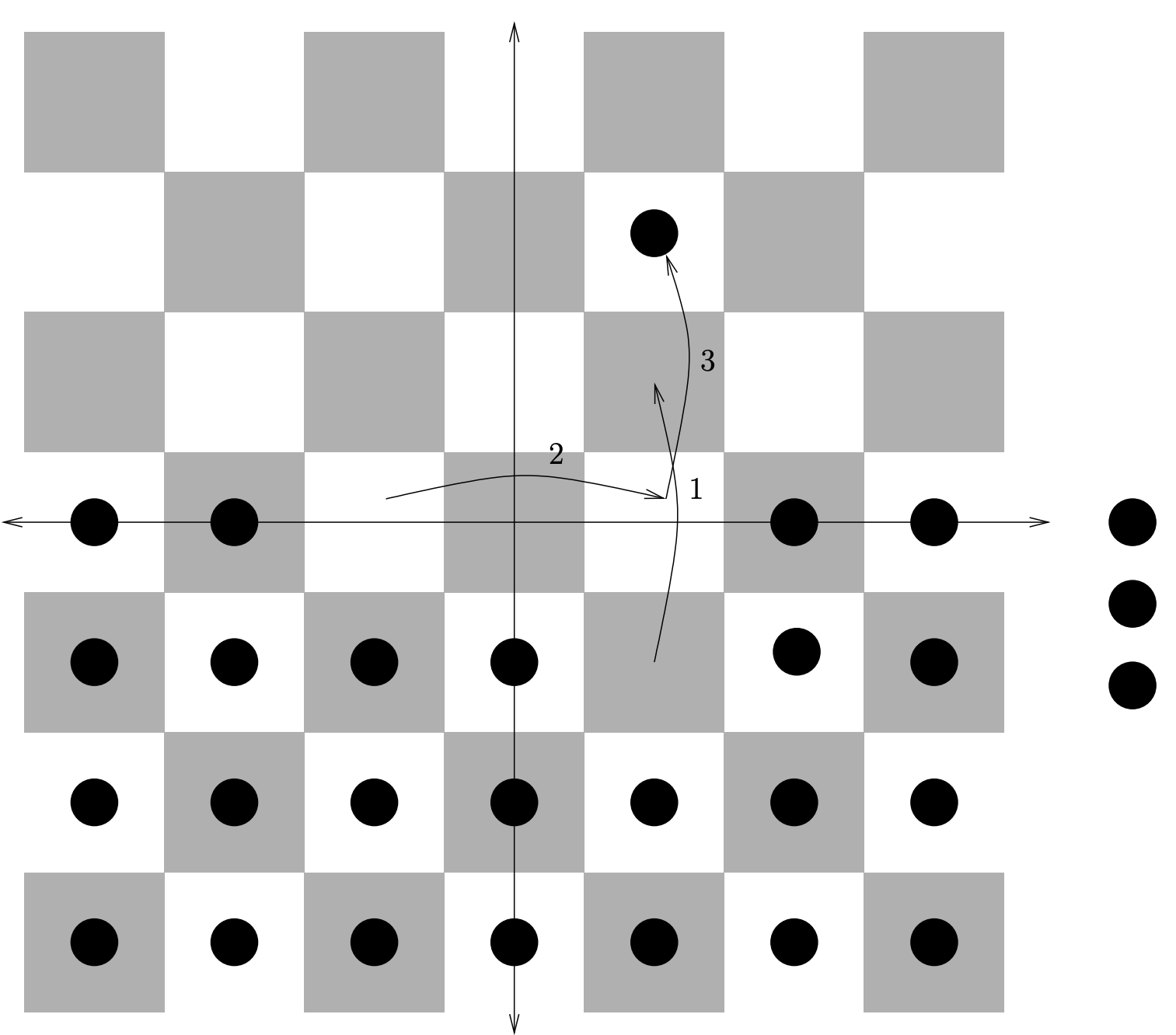
Como una imagen a veces vale literalmente mil palabras, incluimos aquí\(3\) figuras que ilustran los movimientos necesarios para poner un explorador\(1\),\(2\) y\(3\) pasos en el vacío.
Para demostrar que\(8\) los hombres son suficientes para que un explorador\(3\) entre en territorio enemigo, demostramos que es posible reproducir la configuración que puede colocar a un hombre en dos pasos —desplazado hacia arriba por una unidad.
Quizás te sorprenda saber que el patrón de\(8\) los hombres que se necesita para meter a alguien tres pasos en el vacío puede ser recreado, desplazado hacia arriba en una unidad, usando solo\(12\) hombres. Esto significa que podemos conseguir que un hombre\(4\) entre en territorio enemigo usando\(12 + 8 = 20\) hombres. \(16\)Estabas esperando, ¿no? (¡Sé que lo estaba!)
La verdadera sorpresa es que es simplemente imposible meter a un hombre cinco pasos en territorio enemigo. Así que la secuencia que hemos estado viendo realmente va
\( 2, 4, 8, 20, \infty . \)
La prueba de este sorprendente resultado funciona utilizando una estrategia bastante simple, pero inteligente. Asignamos un valor numérico a un conjunto de hombres que depende de sus posiciones —luego mostramos que este valor nunca aumenta cuando hacemos movimientos de “salto corrector ”—, finalmente notamos que el valor asignado a un hombre en posición\((0,5)\) es igual al valor de todo el conjunto original de hombres (que es, con todas las posiciones en el medio plano inferior ocupadas). Esta es una estrategia bastante bonita, pero ¿cómo exactamente vamos a asignar estos valores numéricos?
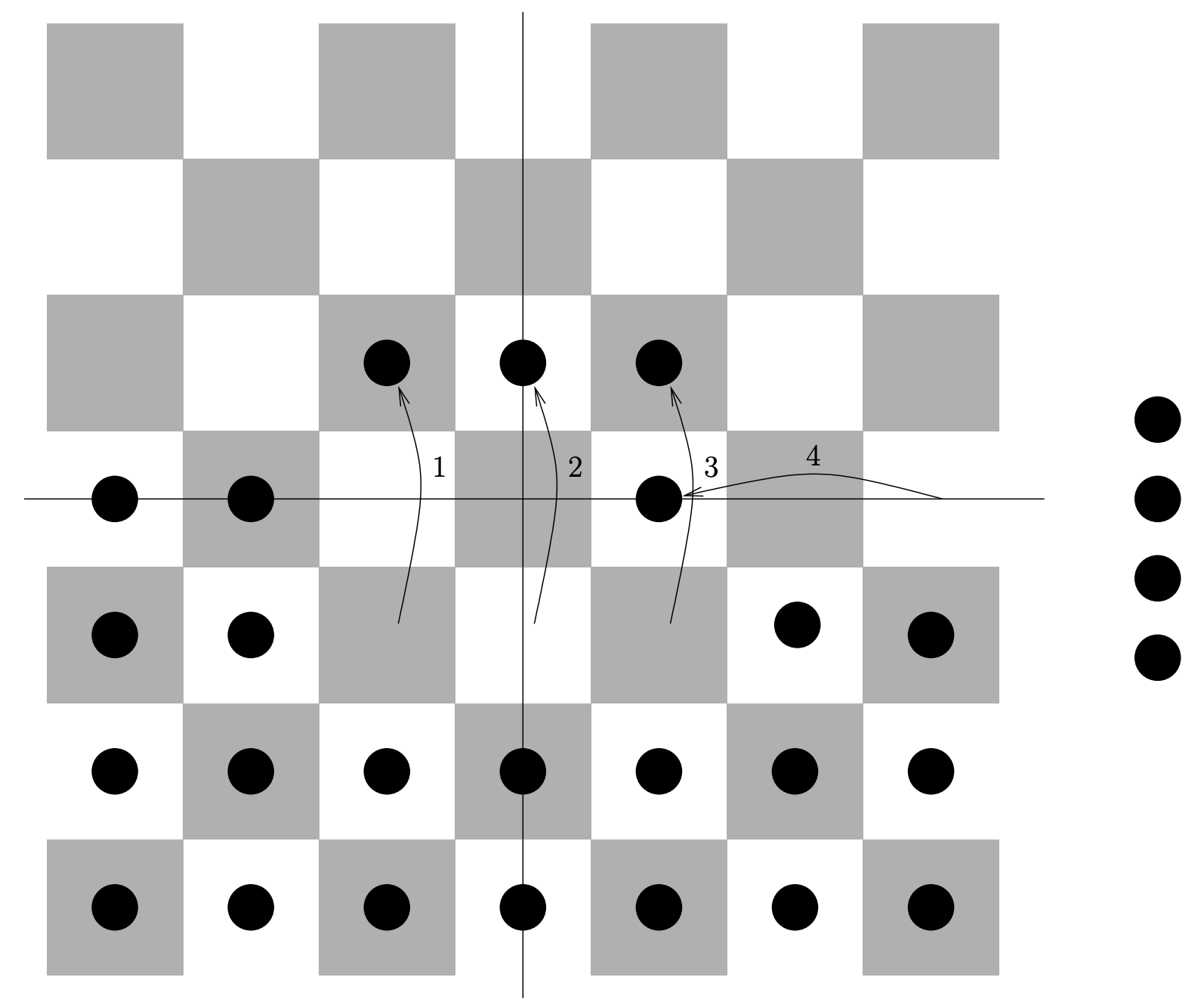
El valor de un hombre está relacionado con su distancia desde el punto\((0,5)\) en lo que a menudo se llama “la métrica del taxicab”. No usamos la distancia en línea recta, sino que determinamos el número de bloques que tendremos que conducir en dirección norte-sur y en dirección este-oeste y sumarlos juntos. El valor de un conjunto de hombres es la suma de sus valores individuales. Ya que tenemos que lidiar con el valor del conjunto de hombres que llena completamente el medio plano inferior, ¡vamos a tener que tener que tener la mayoría de estos valores sean bastante pequeños! Para ponerlo de una manera más madura y digna: la suma infinita de los valores de los hombres de nuestro ejército debe ser convergente.
Anteriormente hemos visto series geométricas que tienen sumas convergentes. Recordemos que la fórmula para tal suma es
\[ \sum_{k=0}^{\infty} ar^k = \dfrac{a}{1-r}, \]
donde\(a\) es el término inicial de la suma y\(r\) es la relación común entre términos.
La gran visión de Conway fue asociar los poderes de algún número\(r\) con las posiciones en el tablero —\(r^k\) va en las plazas que están\(k\) a distancia de la ubicación objetivo. Si tenemos a un hombre que realmente está en la ubicación objetivo, valdrá\(r^0\) o\(1\). Tenemos que hacer arreglos para que sucedan dos cosas: la suma de todos los poderes de\(r\) en la configuración inicial del tablero debe ser menor o igual a\(1\), y los movimientos de salto de cuadros deberían dar como resultado que el valor total de un conjunto de hombres baje o (en el peor de los casos) permanezcan igual. Estos objetivos nos empujan en diferentes direcciones: Para que la suma inicial sea menor que\(1\), nos gustaría\(r\) elegir ser bastante pequeña. Para tener movimientos de salto de cuadros tenemos que elegir\(r\) ser (relativamente) más grandes. ¿Hay un valor de\(r\) eso hace el truco? ¿Podemos encontrar un equilibrio entre estos deseos en competencia?

Piense en el cambio en el valor de nuestro invariante a medida que se hace un movimiento de salto de verificador. Ver Figura\(9.2.6\).
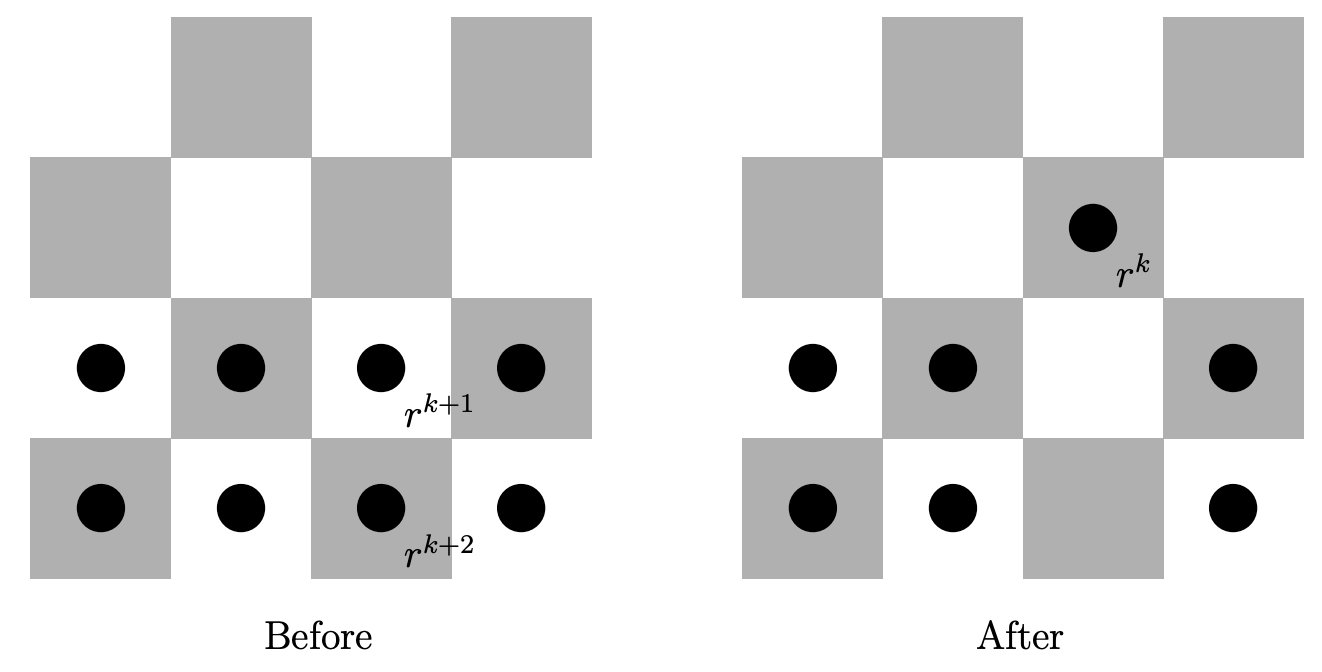
Si elegimos\(r\) para que\(r^{k+2} + r^{k+1} \; \leq \; r^k\) entonces el movimiento de salto de cuadros dejará en el peor de los casos la suma total fija. Tenga en cuenta que siempre y cuando\(r<1\) un movimiento de salto de cuadros que nos aleje de la posición objetivo sin duda disminuirá la suma total.
Como suele ser el caso, analizaremos la desigualdad analizando en cambio la igualdad correspondiente. ¿Qué valor de\(r\) marcas\(r^{k+2} + r^{k+1} = r^k\)? La respuesta es que\(r\) debe ser una raíz de la ecuación cuadrática\(x^2+x-1\).
Hacer el álgebra para verificar la afirmación anterior.
Encuentra el valor de\(r\) que resuelva la ecuación anterior.
Ojalá usaras la fórmula cuadrática para resolver el ejercicio anterior. Por supuesto deberías haber encontrado dos soluciones,\(-1.618033989\ldots\) y\(.618033989\ldots\), estas aproximaciones decimales son en realidad\(-\phi\) y\(\dfrac{1}{\phi}\), donde\(\displaystyle \phi = \frac{1+\sqrt{5}}{2}\) está la famosa “proporción áurea”. Si estamos esperando que la suma sobre todas las posiciones ocupadas de\(r^k\) sea convergente, necesitamos\(|r|<1\), entonces la solución negativa es ajena y así la desigualdad\(r^{k+2} + r^{k+1} \; \leq \; r^k\) es cierta en el intervalo\([\dfrac{1}{\phi}, 1)\).
A continuación queremos mirar el valor de esta invariante cuando los “hombres” ocupan todas las posiciones con\(y\leq0\). Al mirar Figura se\(9.2.5\) puede ver que hay un solo cuadrado con valor\(r^5\), hay\(3\) cuadrados con valor\(r^6\), hay 5 cuadrados con valor\(r^7\), etcétera. La suma,\(S\), de los valores de todas las posiciones inicialmente ocupadas es
\[ S = r^5 \sum_{k=0}^{\infty} (2k+1) r^k. \]
Anteriormente hemos visto cómo resolver por el valor de una suma infinita que involucra poderes de\(r\). En la expresión anterior tenemos poderes de\(r\) pero también multiplicados por números impares. ¿Podemos resolver algo así?
Intentemos el mismo truco que funciona para una suma geométrica. Let
\[ T = \sum_{k=0}^{\infty} (2k+1) r^k = 1 + 3r + 5r^2 + 7r^3 + ... \]
Tenga en cuenta que
\[ rT = \sum_{k=0}^{\infty} (2k+1) r^{k+1} = r + 3r^2 + 5r^3 + 7r^4 + ... \]
y de ello se deduce que
\[ T - rT = 1 + 2 \sum_{k=1}^{\infty} r^{k} = 1 + 2r + 2r^2 + 2r^3 + 2r^4 + ... \]
Un poco más álgebra (y la fórmula para la suma de una serie geométrica) nos lleva a
\[ T = \dfrac{1}{1-r} \left(1 + \dfrac{2r}{1-r} \right), \]
lo que simplifica
\[ T = \dfrac{1+r}{1-r^2}. \]
Por último, recordemos que estamos realmente interesados en\(S = r^5 \cdot T\), o
\[ S = \dfrac{r^5 + r^6}{(1 − r)^2} . \]
Es interesante proceder de esta expresión para\(S\), utilizando el hecho que\(r\) satisface\(x^2 = 1 - x\), para obtener el hecho algo sorprendente de que\(S=1\).
El hecho de que\(S=1\) tenga una consecuencia extraordinaria. Para que un solo verificador llegue al puesto, ¡\((0,5)\)necesitaríamos usar a todos!
Para un conjunto que consiste en un solo corrector posicionado\((0,5)\) al valor de nuestro invariante es\(1\). Por otra parte, el conjunto que consiste en todo el ejército alineado sobre y por debajo del\(x\) eje -también produce un\(1\). Cada movimiento de verificador o bien no cambia el valor del invariante o lo reduce. Lo mejor que podríamos esperar es que no habría necesidad de movimientos del tipo que reduzcan lo invariante —sin embargo todavía no podríamos conseguir que un hombre lo hiciera\((0,5)\) en un número finito de movimientos.
Ejercicios:
Haz el álgebra (¡y muestra todo tu trabajo!) para probar que la invariante definida en esta sección realmente tiene el valor\(1\) para el conjunto de todos los hombres que ocupan el\(x\) eje -eje y el medio plano inferior.
“Escape de los clones” es un bonito rompecabezas, originalmente propuesto por Maxim Kontsevich. El juego se juega en un tablero de ajedrez infinito restringido al primer cuadrante, es decir, los cuadrados pueden identificarse con puntos que tienen coordenadas enteras\((x, y)\) con\(x > 0\) y\(y > 0\). Los “clones” son marcadores (damas, monedas, pequeñas rocas, lo que sea.) que pueden moverse de una sola manera —si los cuadrados inmediatamente arriba y a la derecha de un clon están vacíos, entonces puede hacer un “movimiento clon”. El clon mueve un espacio hacia arriba y se coloca una copia en la celda uno a la derecha. Comenzamos con tres clones ocupando celdas\((1, 1)\),\((2, 1)\) y\((1, 2)\) —nos referiremos a esas tres plazas de tablero de ajedrez como “la prisión”. La pregunta es esta: ¿pueden estos tres clones escapar de la prisión?
Debes demostrar una secuencia de movimientos que libere a los tres clones o proporcionar un argumento de que la tarea es imposible.


