9.3: Teorema del Círculo de Monge

Hay una buena secuencia de acertijos de cerillas que comienza con “Usa nueve cerillas no superpuestas para formar\(4\) triángulos (todos del mismo tamaño)”. No es tan difícil, y después de un tiempo a la mayoría de la gente se le ocurre.

El pateador viene cuando luego les pides que “usen seis fósforos para formar triángulos\(4\) (de igual tamaño)”. Hay una imagen de la solución a este nuevo rompecabezas al final de esta sección. La respuesta implica pensar tridimensionalmente, así que —con ese indicio— pruébalo un rato antes de mirar por atrás.

El teorema del círculo de Monge no tiene nada que ver con los fósforos, pero es un dulce ejemplo de una prueba que funciona moviéndose a una dimensión superior. La gente suele hablar de “pensar fuera de la caja” cuando se habla del pensamiento crítico, pero la idea matemática de pasar a una dimensión superior es aún más poderosa. Cuando tenemos una “caja” en\(2\) -espacio dimensional que luego vemos como sentado en un espacio\(3\) -dimensional encontramos que la caja ya no tiene ni un interior ni un exterior! ¡Obtenemos “fuera de la caja” borrando literalmente la noción de que hay un interior de la caja!

La configuración para el teorema del círculo de Monge consiste en tres círculos aleatorios dibujados en el plano. Bueno, para ser honestos, no pueden ser del todo aleatorios —no podemos permitir un círculo que esté completamente dentro de otro círculo. Porque, si un círculo estuviera completamente dentro de otro, no habría tangentes externas y el teorema del círculo de Monge se trata de tangentes externas.

Probablemente podría escribir unos cientos de palabras para explicar el concepto de tangentes externas a un par de círculos, o simplemente podrías echar un vistazo a Figura\(9.3.1\). Entonces, uhmm, solo echa un vistazo.

Figura\(\PageIndex{1}\): La configuración para el teorema del círculo de Monge: tres círculos colocados aleatoriamente; también estamos mostrando las tangentes externas a un par de círculos. (Copyright; autor vía fuente)

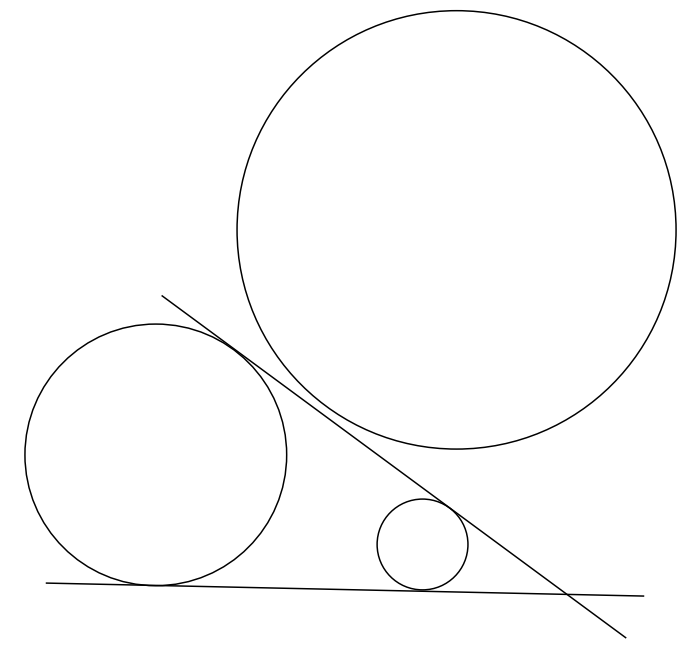
¿Observa cómo las tangentes externas ¹ a dos de los círculos se encuentran en un punto? A menos que los círculos simplemente tengan exactamente el mismo tamaño (¿Y cuáles son las probabilidades de eso?) este va a ser el caso. Cada par de tangentes externas van a encontrarse en un punto. Existen tres pares de tangentes externas y así determinan tres puntos. Supongo, ya que estos tres puntos se determinan de una manera bastante complicada a partir de tres círculos elegidos al azar, eso esperaríamos que los tres puntos fueran más o menos aleatorios. El teorema del círculo de Monge dice que eso no es así.

Teorema\(\PageIndex{1}\): Monge's Circle Theorem

Si se eligen tres círculos de radios diferentes en el plano euclidiano para que ningún círculo quede en el interior de otro, los tres pares de tangentes externas a estos círculos se encuentran en puntos que son colineales.

En Figura\(9.3.2\) vemos un ejemplo completo del teorema del Círculo de Monge en acción. Hay tres círculos aleatorios. Hay tres pares de tangentes externas. Los tres puntos determinados por la intersección de los pares de tangentes externas se encuentran en una línea (mostrada discontinua en la figura).

Ni siquiera intentaremos escribir una prueba formal del teorema del círculo. No es que no se pueda hacer — es solo que probablemente puedas entender mejor el punto a través de una discusión informal.

La idea principal es simplemente pasar al espacio\(3\) -dimensional. Imagínese el plano plano original que contiene nuestros tres círculos aleatorios como el plano\(z=0\) en el\(3\) espacio euclidiano. Reemplazar los tres círculos por tres esferas del mismo radio y teniendo los mismos centros —claramente las intersecciones de estas esferas con el plano\(z=0\) serán nuestros círculos originales. Mientras que los pares de círculos están englobados por dos líneas (las tangentes externas que tanto hemos estado discutiendo), cuando tenemos un par de esferas en el\(3\) espacio, están englobadas por un cono que yace tangente a ambas esferas ². Observe que los conos que se encuentran tangentes a un par de esferas se cruzan con el plano precisamente en esas infames tangentes externas.

Figura\(\PageIndex{2}\): Un ejemplo del teorema del círculo de Monge. Los tres pares de tangentes externas a los círculos se cruzan en puntos colineales. (Copyright; autor vía fuente)

Bueno, bien, nos hemos mudado a\(3\) -d. Hemos reemplazado nuestros círculos por esferas y nuestras tangentes externas por conos tangentes. Los puntos de intersección de las tangentes externas son ahora las puntas de los conos. Pero, ¿de qué sirve todo esto? ¿Hay alguna razón para creer que las puntas de esos conos se encuentran en una línea?

En realidad, ¡sí! Hay un plano que toca las tres esferas tangencialmente. En realidad, hay dos planos de este tipo, uno que los toca a todos en sus superficies superiores y otro que los toca a todos en sus superficies inferiores. ¡Oh, maldición! En realidad hay muchos planos que son tangentes a las tres esferas pero sólo uno que se encuentra por encima de las tres. Ese plano cruza el plano\(z=0\) en una línea —nada elegante ahí; cualquier par de planos no paralelos se cruzará en una línea (y la única forma en que los planos que estamos discutiendo serían paralelos es si las tres esferas simplemente fueran del mismo tamaño). ¡Pero ese plano también yace tangente a los conos que envuelven nuestras esferas y así ese plano (así como el plano\(z=0\)) contiene las puntas de los conos!

Figura\(\PageIndex{3}\): Seis cerillas (en realidad, los lápices son mucho más fáciles de sostener) se pueden organizar tridimensionalmente para crear cuatro triángulos. (Copyright; autor vía fuente)

Ejercicios:

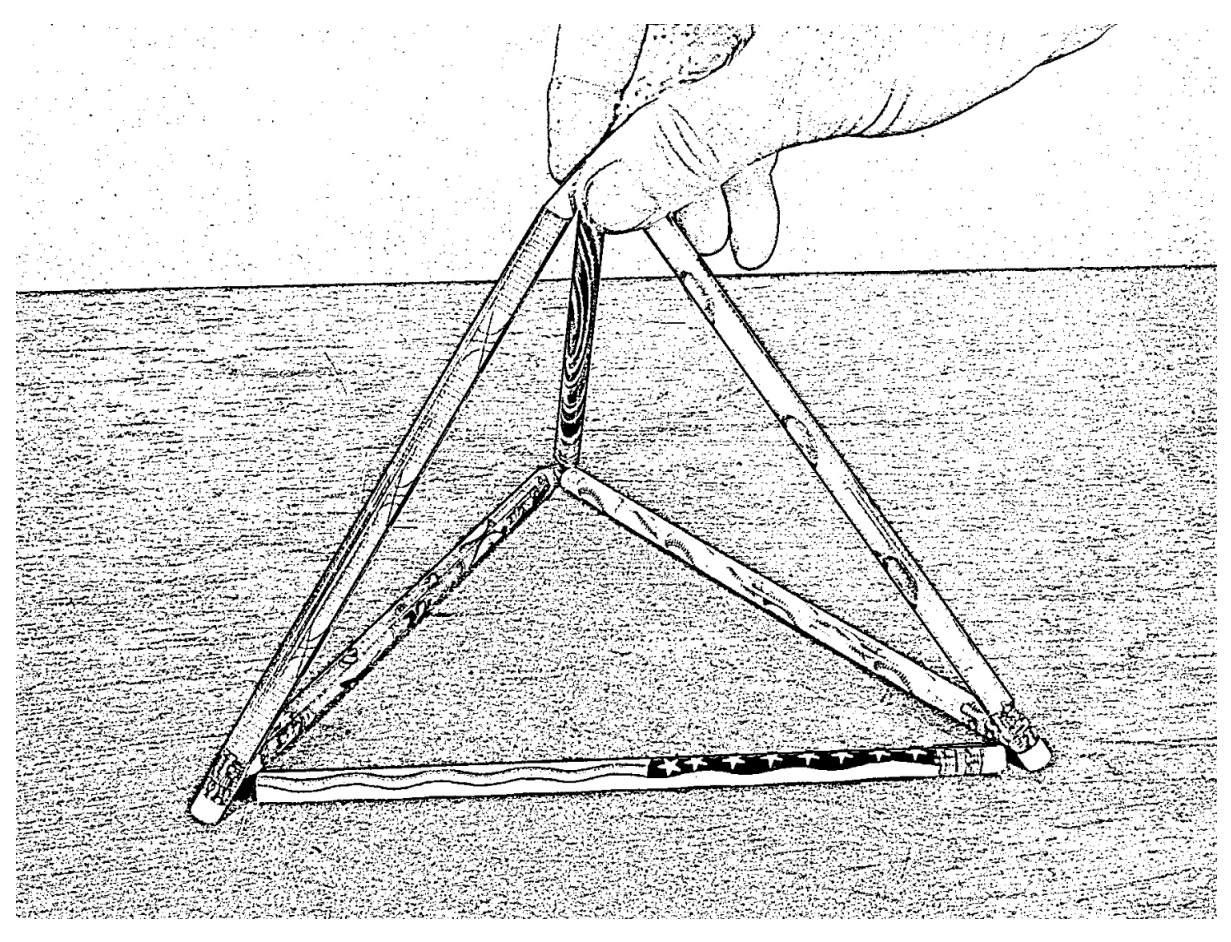
Ejercicio\(\PageIndex{1}\)

Hay un escenario donde la prueba que hemos esbozado para el teorema del círculo de Monge realmente no funciona. ¿Puedes imaginarlo?

Sugerencia

Considera dos esferas relativamente grandes y una que es bastante pequeña.

Notas

1. La razón por la que sigo diciendo “tangentes externas” es que también hay tangentes internas.

2. Como antes, cuando las esferas tienen radios idénticos obtenemos una caja degenerada — el cono se convierte en un cilindro.