1.4: Problemas de encuestas
- Page ID
- 113210
En este conjunto de ejercicios, no estarás trabajando con manipuladores. Construiremos y usaremos diagramas de Venn de una manera diferente para responder preguntas específicas dada una variedad de información.
Vamos a comenzar aprendiendo a construir un diagrama de Venn de dos conjuntos donde
U = {1, 2, 3, 4, 5, 6, 7, 8, 9},
A = {1, 2, 3, 4, 5} y
B = {2, 4, 6, 8}.
El objetivo es construir un diagrama de Venn que muestre la ubicación de todos los elementos en el universo.
Observe que un diagrama de Venn de dos conjuntos en blanco tiene cuatro regiones distintas.
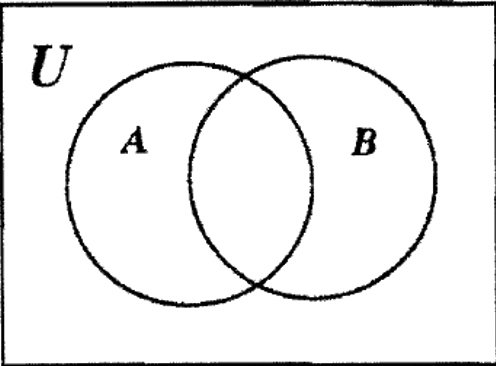
Método 1
Una forma de obtener la solución es decidir dónde colocar cada número, uno a la vez. Comenzando por 1, nótese que sólo está en el conjunto A, y colóquelo en esa región (que notacionalmente es A — B). Entonces puedes averiguar dónde colocar cada uno de los otros ocho elementos uno a la vez. No importa qué elemento coloques primero. Pero, al final, cada uno de los nueve elementos debe colocarse en una de las cuatro regiones. Intente usar este método. Coloca cada uno de los nueve elementos en el diagrama de Venn que se muestra arriba.
Método 2
Aquí hay otra forma de obtener la solución. Como podemos calcular eso\(\bf A \cap B\) = {2, 4}, podemos colocar esos dos elementos en la intersección a la vez, y sabemos que ningún otro número va ahí.

A continuación, observamos que A también contiene los elementos 1, 3 y 5, por lo que ahora podemos rellenar estos elementos en la otra región de A. De igual manera, observamos que B también contiene 6 y 8, por lo que podemos llenar esos elementos en la otra región de B. Esto se muestra a continuación.
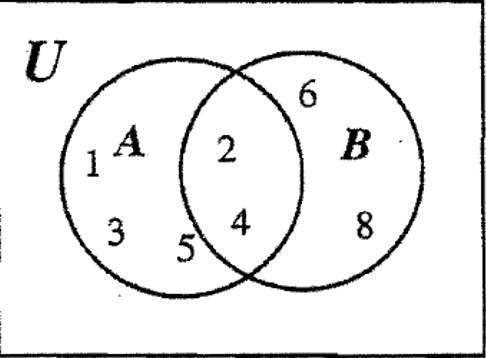
Los únicos elementos en el universo no contabilizados son 7 y 9. Estos van en la parte del universo que no contiene A o B. Después de ponerlos en, todo el diagrama se puede completar como se muestra a continuación. Para verificar, ver si la información original dada anteriormente coincide con la respuesta.
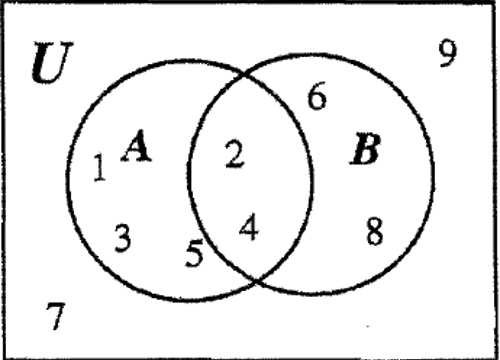
¿Pudiste obtener la respuesta correcta como se muestra arriba usando el primer método propuesto?
Pon cada elemento del universo en su región correcta en el diagrama de Venn a la derecha si U = {1 ,2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 5,7, 9} y B = {1, 2, 5, 6}
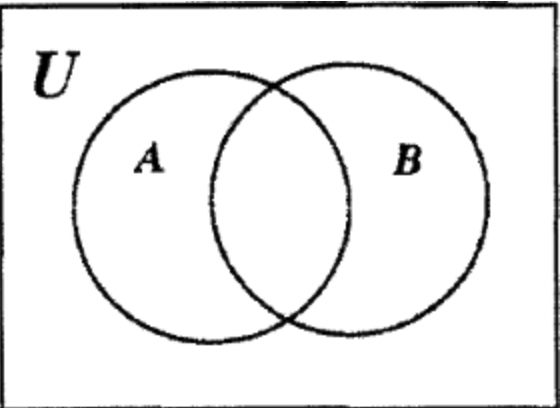
En este siguiente ejemplo, la información se proporciona en una forma diferente. El método 1 es muy difícil de usar cuando los conjuntos A y B no se dan explícitamente. Aún deberíamos poder rellenar el diagrama de Venn. Nuevamente, trabajaremos con dos conjuntos A y B. Al final, vamos a responder a estas preguntas: ¿Qué elementos hay en A, B y U? Se nos da la siguiente información: A — B = {c, d},\(\bf B^{c}\) = {b, c, d, e, f}, B — A = {a, g} y\(\bf A \cup B\) = {a, c, d, g, h}
PASO 1: Dado que A — B y B — A son regiones aisladas, podríamos comenzar rellenando esa información en un diagrama Venn en blanco como se muestra a continuación:
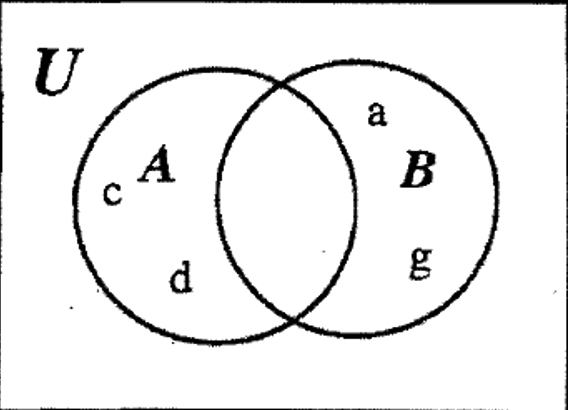
PASO 2: A continuación, podemos rellenar el resto de\(\bf A \cup B\), poniendo el elemento h en la intersección, la región aún no contabilizada.
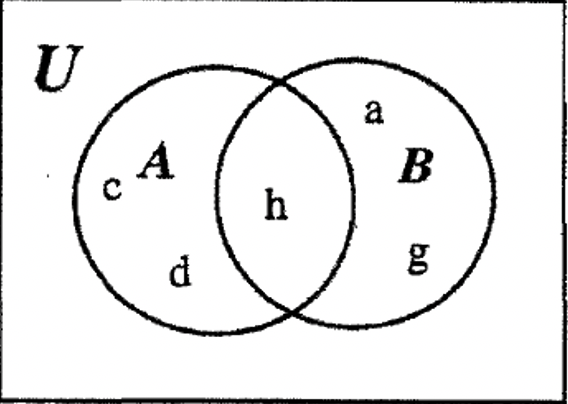
PASO 3: Finalmente, podemos llenar el resto de\(\bf B^{c}\). Tenga en cuenta que hasta el momento, vemos los elementos c y d en una de las regiones de\(\bf B^{c}\), por lo que los elementos restantes b, e y f deben ir en la única región aún no contabilizada como se muestra:
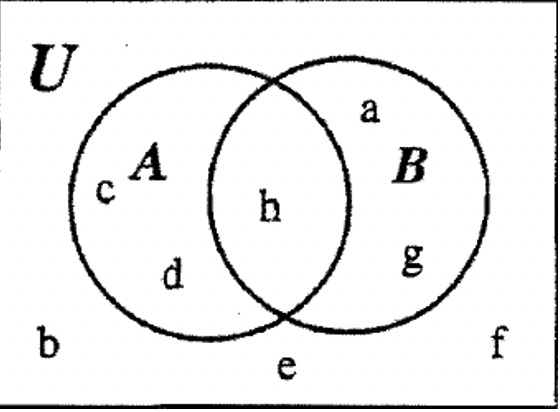
PASO 4: Verifique que la información dada al inicio del problema siga siendo cierta al mirar el diagrama de Venn terminado como se muestra arriba.
PASO 5: Responda a las preguntas formuladas:
U = {a, b, c, d, e, f, g, h}
A = {c, d, h}
B = {a, g, h}
Tenga en cuenta que alguien más podría haber hecho el problema anterior usando diferentes pasos. Hay más de una manera de proceder y aún así llegar a la solución correcta. Deberías volver a intentarlo por tu cuenta. El resultado debe ser el mismo sin importar en qué región llenaste primero.
Haremos un ejemplo más de este tipo, pero esta vez trabajaremos con un diagrama de Venn de tres conjuntos. Dado que hay ocho regiones, tardará un poco más en construirse. La información dada sigue:\(\bf (A \cap B) - C\) = {h}, B — C = {h, n},\(\bf (A \cup B) - C\) = {l, m, h, n}, A — B = {l, m, f},\(\bf A \cap B\) = {g, h, i}, B = {h, n, j, g, i}, C = {f, g, i, j, k} y\(\bf (C \cup B)^{c}\) = {l, m, d, e}
A continuación se muestra solo una forma de dar pasos que conduzcan a la respuesta correcta.
PASO 1: Primero, mira un diagrama de Venn de tres conjuntos en blanco y encuentra una región aislada que pueda rellenar primero a partir de la información dada. \(\bf (A \cap B) - C\)satisface ese criterio y por lo tanto esa región se puede rellenar primero como se muestra a continuación.
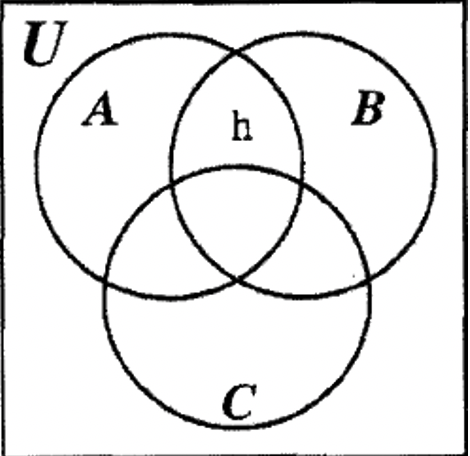
PASO 2: A continuación, B — C se puede completar poniendo el elemento n en la región que no está ya rellenada como se muestra a continuación.

PASO 3: se\(\bf A \cap B\) puede completar ahora también con g e i entrando en la región aún no contabilizada:
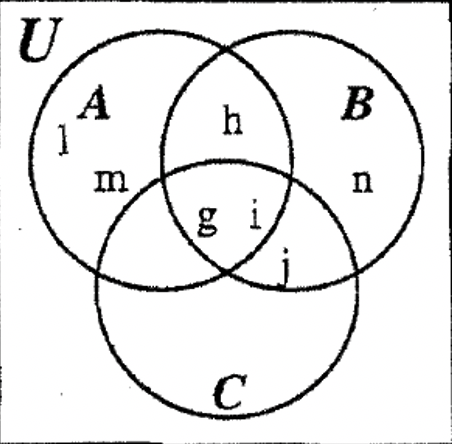
PASO 4: A continuación, podemos rellenar ambos\(\bf (A \cup B) - C\) y B porque también están bajando a regiones aisladas.
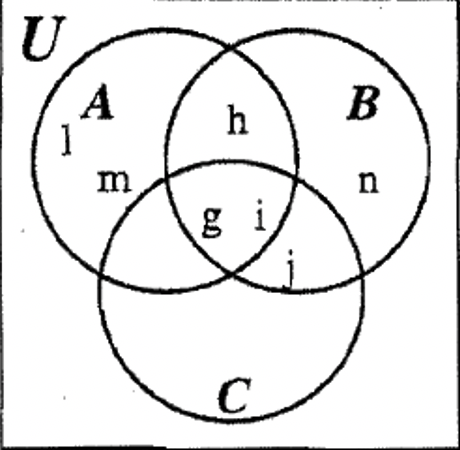
PASO 5: Estamos acercándonos. Sólo quedan tres regiones por rellenar. \(\bf (C \cup B)^{c}\)y la región restante de A — B se puede rellenar como se muestra a continuación:
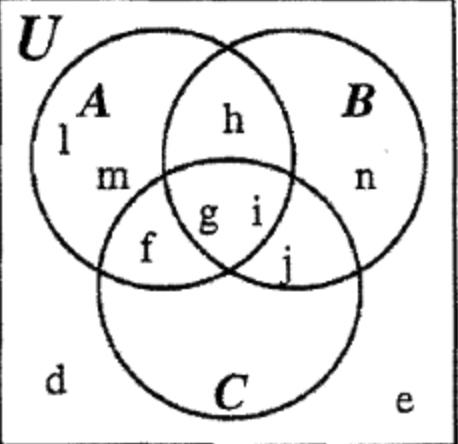
PASO 6: Ahora podemos rellenar la región restante del conjunto C para completar el diagrama.
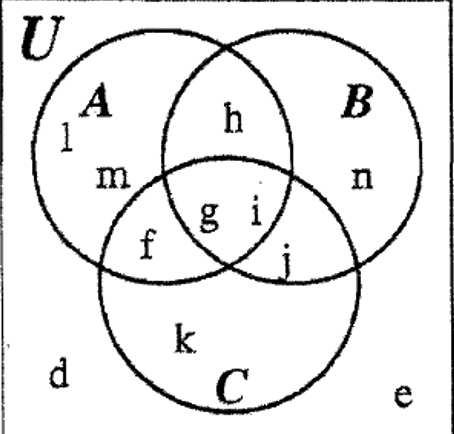
PASO 7: Verifique que toda la información dada siga siendo cierta al mirar este diagrama terminado. Ahora podemos declarar los elementos en los conjuntos A, B, C y U.
| U = {d, e, f, g, h, i, j, k, l, m, n} | A = {f, g, h, i, l, m} |
| B = {g, h, i, j, n} | C = {f, g, i, j, k} |
Dado que U = {a, b, c, d, e, f, g, h, i, j, k}, X = {a, b, c, d, e}, Y = {c, d, f, g, h} y Z = {b, c, h, i, j}, rellenar cada uno de los elementos del universo en su propia región en el diagrama de Venn a la derecha.
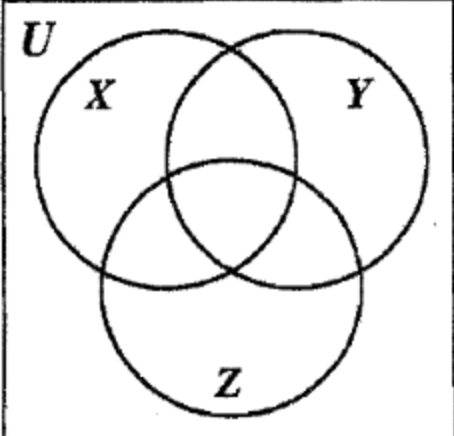
Ahora es un buen momento para que practiques la identificación de las ocho regiones de un diagrama de Venn de tres conjuntos describiendo cada región usando notación de conjunto. Describa cada región como se indica entre paréntesis en el diagrama de Venn. Puede haber más de una manera de describir una región.
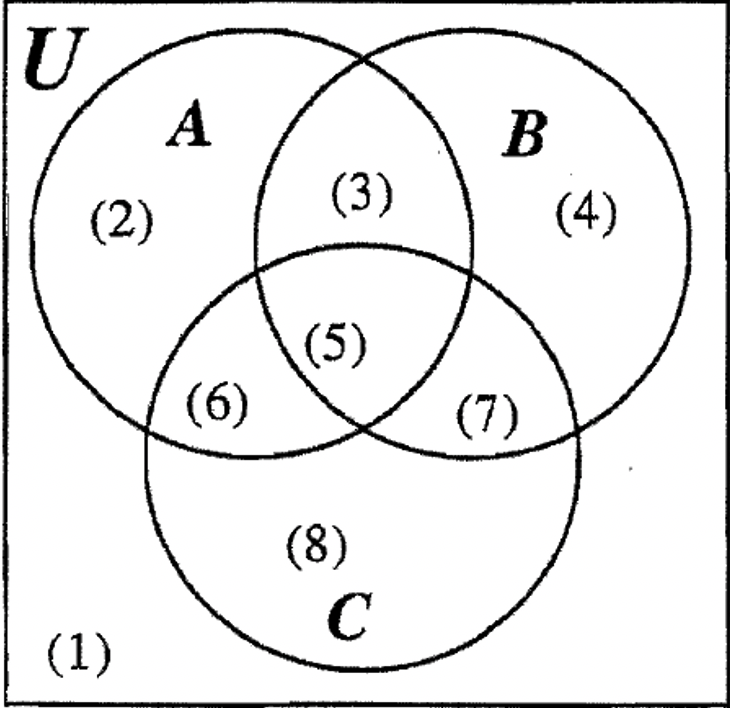
| a. Región 1: _____ |
| b. Región 2: _____ |
| c. Región 3: ______ |
| d. Región 4: ______ |
| e. Región 5: ______ |
| f. región 6: ______ |
| g. Región 7: ______ |
| h. Región 8: _______ |
Antes de pasar a examinar problemas de tipo, necesitamos practicar mirando un diagrama de Venn donde se da la cardinalidad (número de elementos) de cada región y luego poder responder preguntas sobre la cardinalidad de otras combinaciones de regiones.
Mira el diagrama de Venn a continuación y responde las preguntas sobre la cardinalidad de las regiones indicadas.
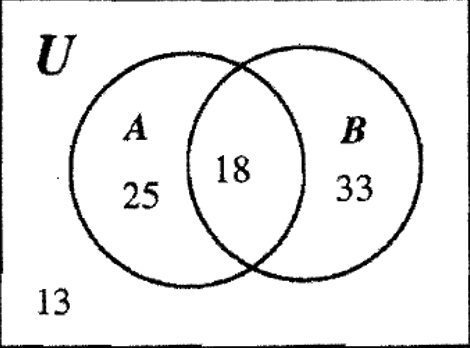
| a.\(n\) (A) = ____ | b.\(n\) (B) = ____ |
| c.\(n\) (\(\bf A^{c}\)) = ____ | d.\(n\) (\(\bf B^{c}\)) = ____ |
| e.\(n\) (\(\bf A \cap B\)) = ____ | f.\(n\) (A — B) = ____ |
| g.\(n\) (\(\bf (A \cup B)^{c}\)) = ____ | h.\(n\) (U) = ____ |
Imagínese que el problema anterior era realmente un modelo para qué tipo de fruta empacaba un grupo de personas en sus almuerzos. A representaba a los que empacaban manzanas y B representaba a los que empacaban plátanos. Supongamos que las manzanas y los plátanos son el único tipo de fruta disponible. Entonces las preguntas que respondiste fueron estas:
- ¿Cuántas manzanas empacadas?
- ¿Cuántos plátanos empacados?
- ¿Cuántas manzanas no empacaron?
- ¿Cuántos no empacaron plátanos?
- ¿Cuántos empacaron ambos tipos de fruta?
- ¿Cuántas manzanas empacadas solamente?
- ¿Cuántos no empacaron ninguna fruta?
- ¿Cuántas personas fueron encuestadas?
Mira para ver si habrías buscado en las mismas regiones si las preguntas se hubieran hecho de esta manera.
Veamos qué tan bien te va trabajando con un diagrama de Venn de tres conjuntos. El diagrama de Venn a continuación muestra la cardinalidad de cada región. Una encuesta a estudiantes universitarios mostró las calificaciones que recibieron en su última boleta de calificaciones. A significa obtener una A, B significa obtener una B y C significa obtener una C. Algunas personas tomaron solo un curso mientras que otras tomaron más. Mira el diagrama de Venn y responde las siguientes preguntas. Crédito Extra: En lugar de solo escribir el número, anote simbólicamente lo que se hace la pregunta. Es decir, si la pregunta es “¿Cuántos recibieron tanto A como B?” escribirías\(n\) (\(\bf A \cap B\)) = 51.
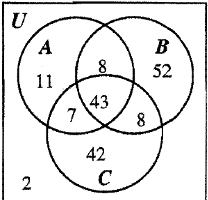
| a. ¿Cuántos tienen todas las A? ____ |
| b. ¿Cuántos tienen A? ____ |
| c. ¿Cuántos tienen B y C? ____ |
| d. ¿Cuántos tienen solo A o B? _____ |
| e. ¿Cuántos no obtuvieron una C? _____ |
| f. ¿Cuántos tienen B o C? _____ |
| g. ¿Cuántos tienen B, pero no C? ____ |
| h. ¿Cuántos obtuvieron al menos dos grados diferentes de A, B o C? ____ |
| i. ¿Cuántos obtuvieron exactamente dos grados diferentes de A, B o C? ____ |
En otra encuesta, se hicieron preguntas para ver cuántas personas había en su adolescencia, cuántas estaban casadas y cuántas tenían hijos. T representa a adolescentes, M representa a los que estaban casados y C representa a los que tienen hijos. Mira el diagrama de Venn que muestra la cardinalidad de cada región para responder a las siguientes preguntas:
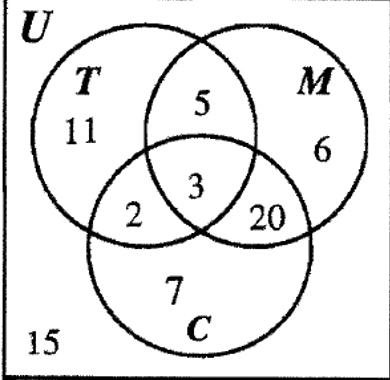
- ¿Cuántas personas se casaron? ____
- ¿Cuántos adolescentes tuvieron hijos? ____
- ¿Cuántas personas había en la encuesta? ____
- ¿Cuántas personas no tuvieron hijos? ____
- ¿Cuántos adolescentes no se casaron? ____
- ¿Cuántos adolescentes se casaron y tenían hijos? ____
- ¿Cuántos adolescentes había en la encuesta? ____
- ¿Cuántas personas estaban solteras y tenían hijos? ____
- ¿Cuántas personas se casaron y tenían hijos? ____
Al inicio de este conjunto de ejercicios, aprendiste a colocar elementos en sus regiones adecuadas dada la información sobre los elementos en algunos conjuntos. El mismo proceso se puede utilizar cuando sólo se considera la cardinalidad de un conjunto o región. Haremos un ejemplo involucrando dos conjuntos, C y B, donde\(n\) (U) = 35,\(n\) (C) = 20,\(n\) (B) = 15 y\(n\) (B — C) = 10.
PASO 1: Nuevamente, primero tenemos que aislar una región. B — C es una región aislada y así podemos llenar 10 en ese lugar como se muestra en el Venn a continuación:
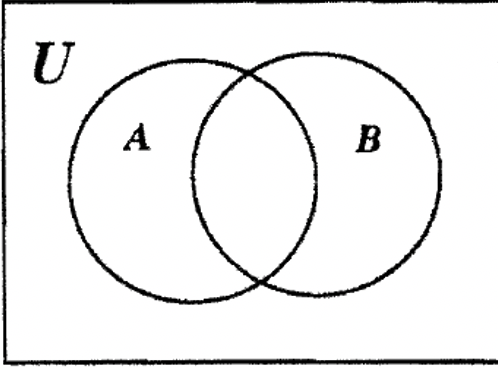
PASO 2: Podemos llenar 5 en la otra región de B ya que B tiene un total de 15 elementos (10 + 5 = 15).
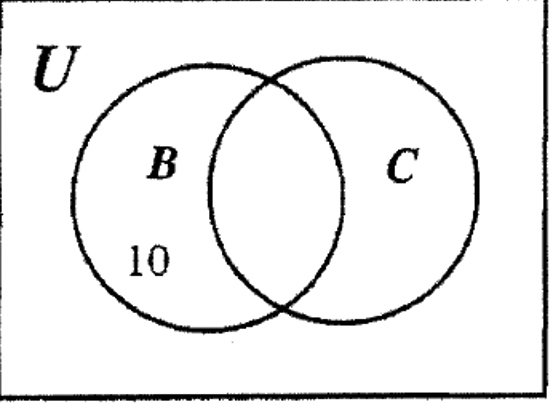
PASO 3: Dado que C tiene un total de 20 elementos, podemos rellenar la otra región de C con el número 15.
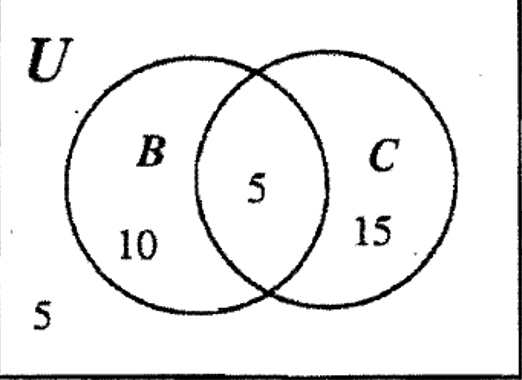
PASO 4: Solo queda una región por llenar y como el número total de elementos es 35, la región final a rellenar debe ser 5.
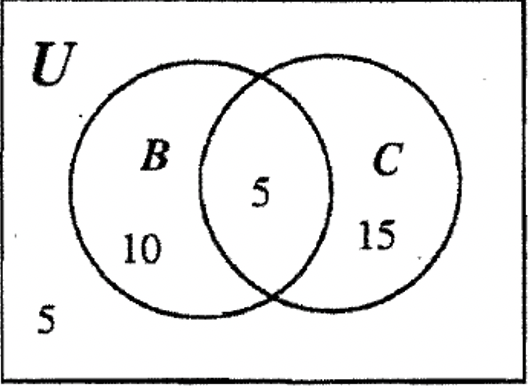
Por lo general, el problema anterior habría sido un problema de palabras redactado algo como esto:
Se encuestó a una clase de 35 alumnos y se determinó que 20 alumnos eran dueños de un automóvil, 15 tenían una bicicleta y 10 de los que poseían una bicicleta no tenían automóvil. ¿Cuántos estudiantes poseían tanto una bicicleta como un automóvil? ¿Cuántos estudiantes solo poseían un auto? ¿Cuántos estudiantes no poseían ni una bicicleta ni un automóvil?
Para responder a estas preguntas, se podría considerar dibujar un diagrama de Venn que contenga dos conjuntos, C y B, donde C representaría el número de estudiantes que poseen autos y B representaría el número de estudiantes que poseen bicicletas. ¡Observe que el primer paso sería definir sus variables! A continuación, después de leer la información dada, se podría concluir que la información podría escribirse simbólicamente así:\(n\) (U) = 35,\(n\) (C) = 20,\(n\) (B) = 15 y\(n\) (B — C) = 10. ¿Esto le resulta familiar? A partir de aquí, los pasos serían exactamente los mismos que acabamos de hacer en el ejemplo anterior. La persona podría entonces mirar el diagrama de Venn y responder a las preguntas formuladas.
- ¿Cuántos estudiantes poseían tanto una bicicleta como un automóvil? (Mira\(\bf B \cap C\)):\(\underline{5}\)
- ¿Cuántos estudiantes solo poseían un auto? (Mira C — B)):\(\underline{15}\)
- ¿Cuántos estudiantes no poseían ni una bicicleta ni un automóvil? (Mira\((\bf B \cup C)^{c}\)):\(\underline{5}\)
Se encuestó a veinte preescolares sobre si tenían o no perros y/o gatos como mascotas en su hogar. Diez niños eran dueños de ambos animales. Cuatro no tenían mascotas en casa y 14 perros de propiedad. Construye un diagrama de Venn que represente cuántos tenían cada tipo de animal y contesta las preguntas hechas en función de tu diagrama. ¡Usa letras significativas para representar tus conjuntos!
| a. ¿Cuántos niños poseían gatos? |
| b. ¿Cuántos niños poseían gatos solamente? |
| c. ¿Cuántos niños no tenían un perro? |
Ahora es el momento de practicar la construcción de un diagrama de Venn de tres conjuntos dada la siguiente información proporcionada sobre tres conjuntos, A, B y C:
| \(n\)(\(\bf (A \cap B) - C)\)= 2 | \(n\)(B — C) = 8 |
| \(n\)(A — B) = 7 | \(n\)(A) = 13 |
| \(n\)(\(\bf A - (B \cup C)\)) = 4 | \(n\)(B) = 20 |
| \(n\)(C — B) = 13 | \(n\)(U) = 42 |
Construiremos un diagrama de Venn mostrando la cardinalidad de cada región y luego encontraremos:
| a.\(n\) (\(\bf (B \cap C)\)) |
| c.\(n\) (\(\bf B^{c}\)) |
| e.\(n\) (\(\bf (A \cup C) - B\)) |
| f.\(n\) (\(\bf (C - (A \cup B)\) |
| g.\(n\) (A) |
| h.\(n\) (\(\bf (A \cup B \cup C)^{c})\) |
| b.\(n\) (A — C) |
| d.\(n\) (C) |
PASO 1: Dibuja un diagrama de Venn de tres conjuntos y ve si alguna de la información proporcionada es lo suficientemente específica como para cubrir solo una región. \(\bf (A \cap B) - C\)y\(\bf A - (B \cup C)\) cada uno cubre una región así que rellene esas regiones primero.
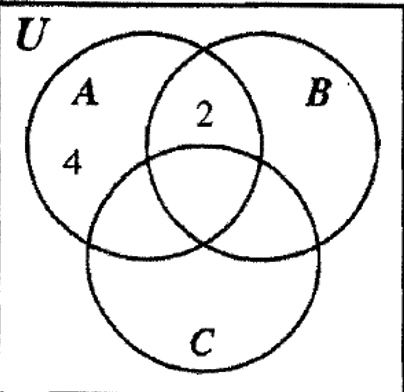
PASO 2: B — C y A — B tienen cada una dos regiones con una región de cada una ya rellenada. Las dos regiones de B — C deben sumar hasta 8 de manera que deja 6 para la otra parte. De igual manera, las dos regiones de A — B deben sumar hasta 7 dejando 3 para la otra región.
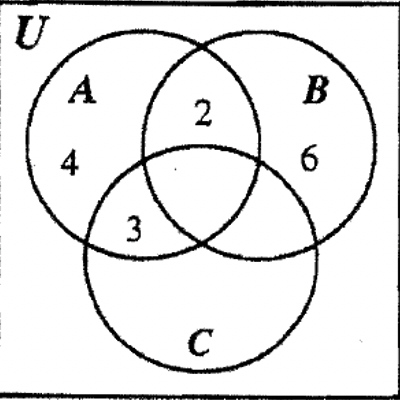
PASO 3: A tiene tres de sus cuatro regiones rellenadas ahora, por lo que podemos llenar 4 en la última región de A ya que\(n\) (A) = 13, lo que significa que las cuatro regiones de A deben sumar 13.
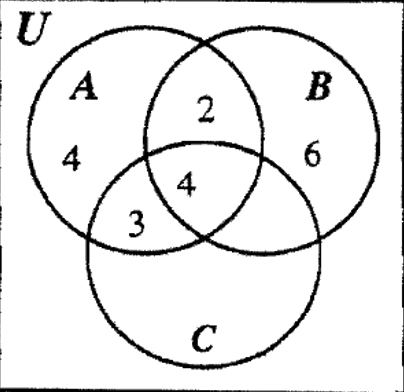
PASO 4: Tenga en cuenta que B tiene todas menos una de sus regiones rellenadas ahora, por lo que podemos llenar esa última región con 8 ya que\(n\) (B) = 20.
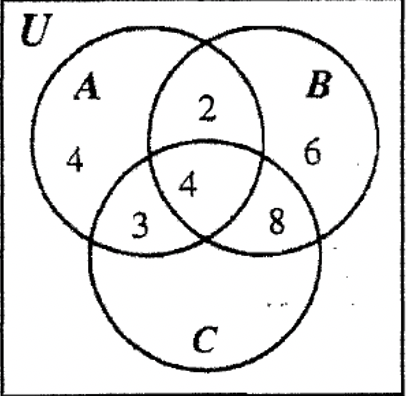
PASO 5: Dado que\(n\) (C — B) = 13 y una de las dos regiones de C — B es 3, eso deja 10 para ser llenado en la otra región.
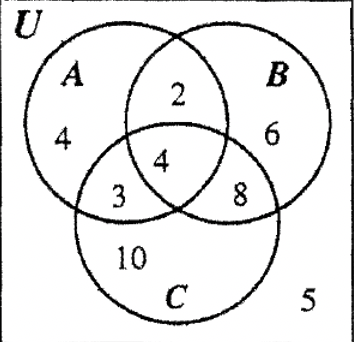
PASO 6: Solo queda una región por rellenar y como el universo contiene 42 elementos, quedan 5 elementos por contabilizar. Esto completa esta parte del proceso.

PASO 7: ¡Este paso es muy importante! Asegúrate de regresar y revisar tu trabajo con mucho cuidado. Al inicio del problema se dieron ocho datos. Regresa y revisa cada uno individualmente. Por ejemplo, asegúrate de que cuando mires tu diagrama completado, sigue siendo cierto que\(n\) (B — C) = 8,\(n\) (A — B) = 7,\(n\) (A) = 13,\(n\) (\(\bf A - (B \cup C)\)) = 4,\(n\) (C — B) = 13, etc.
PASO 8: Mira el diagrama de Venn completado y ahora responde a las preguntas planteadas:
| a.\(n\) (\(\bf B \cap C\)) = 12 |
| b.\(n\) (A — C) = 6 |
| c.\(n\) (\(\bf B^{c}\)) = 22 |
| d.\(n\) (C) = 25 |
| e.\(n\) (\(\bf (A \cup C) - B\)) = 17 |
| f.\(n\) (\(\bf (C - (A \cup B)\)) = 10 |
| g.\(n\) (A) = 13 |
| h.\(n\) (\(\bf (A \cup B \cup C)^{c}\)) =5 |
Más a menudo, el problema anterior se habría presentado como un problema tipo encuesta donde las respuestas podrían responderse usando la teoría de conjuntos. Consideremos el siguiente ejemplo.
Se realizó una encuesta a 42 hombres preguntando por sus gustos de ciertos nombres femeninos: Amy, Beth y Cindy. Se descubrió que a 13 hombres les gustaba el nombre Amy, a 20 de ellos le gustaba Beth, a 8 le gustaba Beth pero no Cindy, a 13 le gustaba Cindy pero no Beth, a 7 le gustaba Amy pero no a Beth, a 4 le gustaba solo el nombre Amy y a 2 le gustaba Amy y Beth pero no el nombre Cindy. Encuentra lo siguiente:
- ¿A cuántos hombres les gustaron tanto los nombres Beth como Cindy?
- ¿A cuántos hombres les gustó el nombre Amy pero no el nombre Cindy?
- ¿A cuántos hombres no les gustó el nombre Beth?
- ¿A cuántos hombres les gustó el nombre Cindy?
- ¿A cuántos hombres no les gustó el nombre Beth, pero le gustó al menos uno de los otros nombres?
- ¿A cuántos hombres les gustó solo el nombre Cindy?
- ¿A cuántos hombres les gustó el nombre Amy?
- ¿A cuántos hombres no les gustó ninguno de los nombres?
Este problema podría resolverse dejando primero que las letras A, B y C representen los conjuntos de hombres a los que les gustaron los nombres Amy, Beth y Cindy, respectivamente. A continuación, podrías escribir las ocho pistas dadas usando notación set, ¡que te dará exactamente las mismas ocho pistas dadas al inicio del ejemplo anterior! O bien, podrías ir directamente a un diagrama de Venn, decidir a qué parte del diagrama de Venn está vinculada cada pista y comenzar a rellenar los números. Las preguntas formuladas también son exactamente las mismas que en el ejemplo anterior. Prueba este problema en este formulario y luego revisa tus respuestas mirando hacia atrás en el ejemplo anterior. Asegúrate de que puedes hacer esto con éxito por tu cuenta antes de probar los siguientes dos ejercicios.
Se realizó una encuesta a 60 estudiantes universitarios preguntando qué comidas comían regularmente en la escuela. Treinta alumnos suelen desayunar en la escuela, 26 suelen almorzar allí
y 23 generalmente cenaban en la escuela. Seis alumnos dijeron que comieron las tres comidas en la escuela. Once comieron tanto el desayuno como el almuerzo mientras que 15 solo desayunaron en la escuela y 12 solo almorzaron allí. Etiquete los conjuntos y complete el diagrama de Venn que aparece a continuación representando esta información y responda las siguientes preguntas:
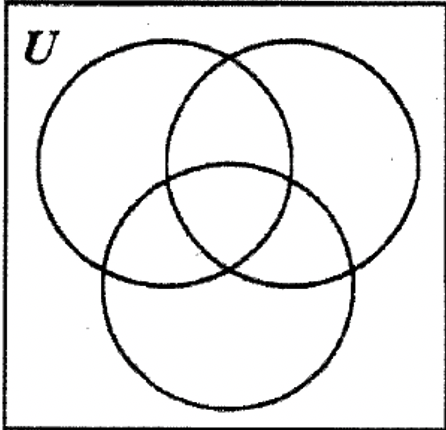
| a. ¿Cuántos alumnos comieron tanto el almuerzo como la cena en la escuela? |
| b. ¿Cuántos no comieron en la escuela? |
| c. ¿Cuántos solo cenaron en la escuela? |
| d. ¿Cuántos desayunaron y/o cenaron en la escuela? |
| e. ¿Cuántos comieron exactamente una comida en la escuela? |
| f. ¿Cuántos comieron al menos dos comidas en la escuela? |
| g. ¿Cuántos comieron tanto el almuerzo como la cena en la escuela, pero no desayunaron? |
A otro grupo de estudiantes se le preguntó qué viejas repeticiones de Dick Van Dyke, Gilligan's Island y The Honeymooners les gustaba ver en la televisión nocturna. A 34 les gustó tanto Dick Van Dyke como Gilligan's Island mientras que a 7 le gustaba solo Dick Van Dyke y a 11 le gustaba solo Gilligan's Island. A 15 les gustó Dick Van Dyke pero no a Gilligan's Island mientras que a 21 le gustaba Gilligan's Island pero no Dick Van Dyke. A 27 no le gustó The Honeymooner's pero le gustó al menos uno de los otros programas. A 31 no le gustó The Honeymooners y a 20 les gustó The Honeymooners pero no a Gilligan's Island. Etiquete los conjuntos y complete el diagrama de Venn que aparece a continuación representando esta información. Luego, conteste las siguientes preguntas:

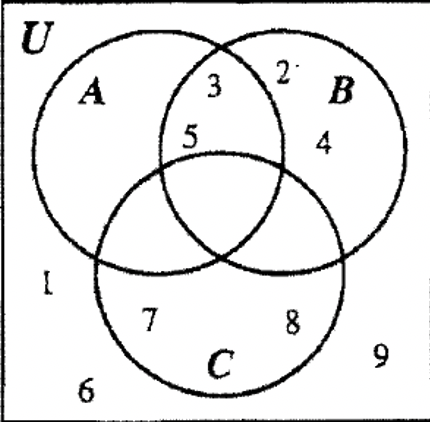
Al trabajar con diagramas de Venn hasta ahora, básicamente hemos restringido la imagen a tres conjuntos y hemos mostrado la misma plantilla una y otra vez donde los conjuntos se superponen entre sí. Para un problema en particular, un diagrama de Venn podría representarse de manera muy diferente. Por ejemplo, considere U = {1, 2, 3, 4, 5, 6, 7, 8, 9} con los subconjuntos A, B y C definidos de la siguiente manera:
A = {3, 5}, B = {2, 3, 4, 5} y C= {7, 8}. Podríamos mostrar los elementos del universo en las dos formas que se muestran a continuación. El Venn de la izquierda muestra la forma convencional como lo hemos estado haciendo para este conjunto de ejercicios mientras que el de la derecha es en realidad un poco más específico porque queda claro a partir de la imagen que\(\bf A \subset B\) y que C no tiene elementos en común con A o B.
 |
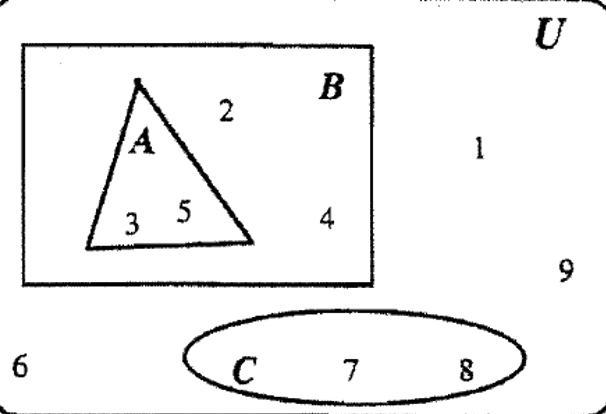 |
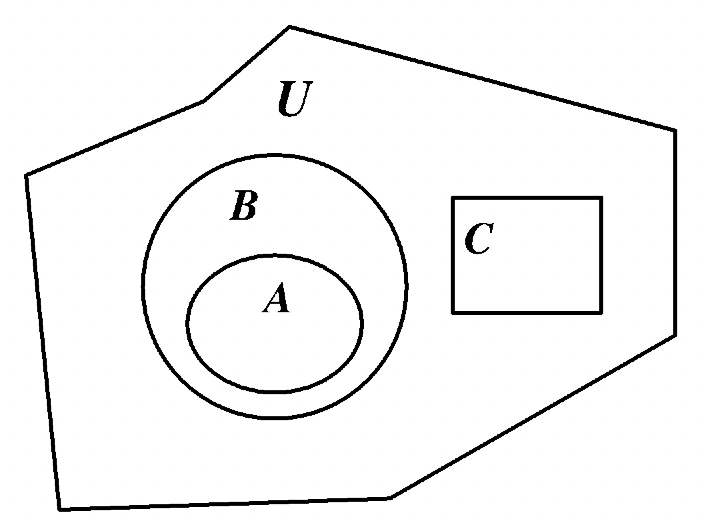
Es especialmente útil poder dibujar un diagrama de Venn como el segundo diagrama de Venn que se muestra arriba cuando se le pide que haga algo como esto: Dibuja un diagrama de Venn que contenga los conjuntos A, B y C de tal manera que\(\bf A \subset B\) con C no tenga elementos en común con A o B. Observe que no se le dan los elementos específicos de A y B. El diagrama de la derecha muestra una forma de representar esta información.
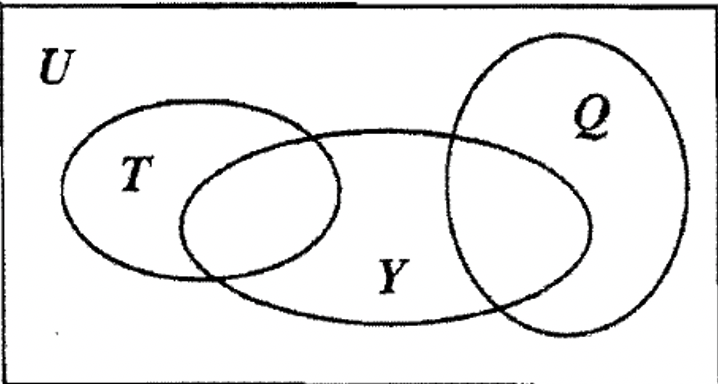
Considere estos subconjuntos de los bloques A: Amarillo, Triángulo y Cuadrado. Una forma de mostrar cómo podrían organizarse en un diagrama de Venn se muestra en el Venn a la derecha. Triángulos y Cuadrados son disjuntos entre sí, mientras que ambos Triángulos y Cuadrados se cruzan con Amarillo.
En el espacio de abajo, organice estos subconjuntos de los bloques A, Rojo (R), Verde (G) y Círculo (C) en un diagrama de Venn que muestre claramente su relación entre sí.
En el espacio de abajo, organice estos subconjuntos de los bloques A, Verde (G), Amarillo (Y), Azul (B), Rojo (R), Pequeño (S), en un diagrama de Venn que muestre claramente su relación entre sí.
Sea U = {1, 2, 3, 4, 5, 6, 7, 8, 9} con estos subconjuntos: A = {6, 7, 8}, B = {2, 3}, C = {3, 4}, D = {5}, E = {1, 2, 3, 4, 5, 6}. En el espacio de abajo, organice estos conjuntos en un diagrama de Venn que muestre claramente su relación entre sí. Es un poco complicado porque hay cinco subconjuntos, ¡pero puedes hacerlo!


