1.5: Tarea
- Page ID
- 113205
- Envíe la tarea por separado de este libro de trabajo y grapa todas las páginas juntas. (Un elemento básico para la presentación completa de toda la tarea de la unidad)
- Inicie un nuevo módulo en la parte frontal de una nueva página y escriba el número de módulo en la parte superior central de la página.
- Las respuestas sin apoyar el trabajo no recibirán crédito.
- Algunas soluciones se dan en el manual de soluciones.
- Puedes trabajar con compañeros de clase pero hacer tu propio trabajo.
Sea U = {a, c, e, m n, r, u, v, w, x, z} con los subconjuntos A, B, C y D definidos a continuación: A = {m, n, r, u, x} B = {a, c, r, u, x} C = {e, v, w, x, z} D = {a, c, z} Usando la notación correcta, buscar los siguientes, mostrar todos los trabajos
| a.\(\bf B \cap D\) | f.\(\bf A - C^{c}\) | k.\(\bf (A \cap D) - B^{c}\) |
| b.\(\bf A \cap D\) | g.\(\bf B - (A \cap C)\) | l. n (\(\bf A \cup B\)) |
| c. C - B | h.\(\bf D^{c} - (B \cup C)\) | m. n (A) + n (B) |
| d.\(\bf (A \cup C)^{c}\) | i.\(\bf (A \cap B) \cap (C \cup D)\) | n. n (D - C) |
| e.\(\bf D^{c} \cap B\) | j.\(\bf (B^{c} \cup D)^{c}\) | o. n (\(\bf B \cap C\)) |
Sea U = {a, c, e, m n, r, u, v, w, x, z} con los subconjuntos A, B, C definidos de la siguiente manera:
| A = {m, n, r, u, v} | B = {r, u, w, x} | C = {n, r, x, c} |
Dibuja un Diagrama de Venn y coloca cada elemento del universo en la región correcta
Utilice las leyes de DeMorgan para reescribir cada una de las siguientes acciones:
| a.\(\bf N \cup P^{c}\) | b.\(\bf R^{c} \cap S\) |
Utilice las propiedades distributivas de conjuntos para reescribir cada uno de los siguientes elementos:
| a.\(\bf (A^{c} \cup E) \cap (A^{c} \cup F)\) | b.\(\bf B \cap (A \cup C)\) |
Se realizó una encuesta para determinar cuál de las tres bebidas (té, leche y/o café) bebía cada día. Los resultados fueron los siguientes:
| 7 solo bebieron café | 6 bebieron los tres | 11 bebió té y café |
| 21 bebieron café | 4 no bebieron ninguno de los tres | 9 no bebió ni café ni té |
| 21 bebió té | 1 bebió solo té y leche |
| a. Dibuje un diagrama de Venn que indique cuántas personas pertenecerían en cada región. Etiquete los tres conjuntos con letras significativas. |
| b. ¿Cuántas personas fueron encuestadas? |
| c. ¿Cuántos bebieron leche? |
| d. ¿Cuántos bebieron solo café y leche? |
| e. ¿Cuántos bebieron sólo leche? |
| f. ¿Cuántos bebieron té o café pero no leche? |
| g. ¿Cuántos bebieron exactamente dos tipos de bebidas? |
| h. ¿Cuántos no tomaron leche ni té? |
Saque sus bloques A y organícelos en subconjuntos para que cada subconjunto solo contenga elementos que tengan el mismo tamaño y color.
| a. ¿Cuántos subconjuntos hay? | b. ¿Cuántas piezas hay en cada subconjunto? |
Deje que A, B y C representen cualquier conjunto. Conteste Verdadero o Falso para las siguientes afirmaciones. Para que una afirmación sea cierta, debe ser siempre cierta. Por cada declaración False, dar un ejemplo de por qué es Falso.
| a. B es siempre un subconjunto de\(\bf A \cup B\) |
| b.\(\bf (A - B)^{c} = A^{c} - B^{c}\) |
| c. B es siempre un subconjunto de\(\bf A \cap B\) |
| d.\(n\) (\(\bf A \cup B\)) =\(n\) (A) +\(n\) (B) |
| e.\(n\) (\(\bf A \cup B)\)=\(n\) (A) +\(n\) (B) —\(n\) (\(\bf A \cap B\)) |
| f. Si\(n\) (\(\bf A \cup B\)) =\(n\) (A) +\(n\) (B), entonces A y B son disjuntos. |
Dibuja un diagrama de Venn y sombrea en la región que representa lo siguiente
| a.\(\bf (C \cup A) - B\) | b.\(\bf (C \cap B) \cup A\) | c.\(\bf (C \cap B) - A\) |
| d.\(\bf (A \cup C) \cap B\) | e.\(\bf \bar{A} - (B \cap C)\) | f.\(\bf (B - A) \cap (B - C)\) |
Identificar el área sombreada de cada diagrama de Venn por notación de conjunto.
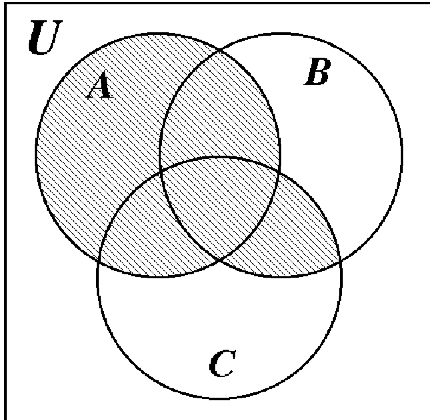 a. a. |
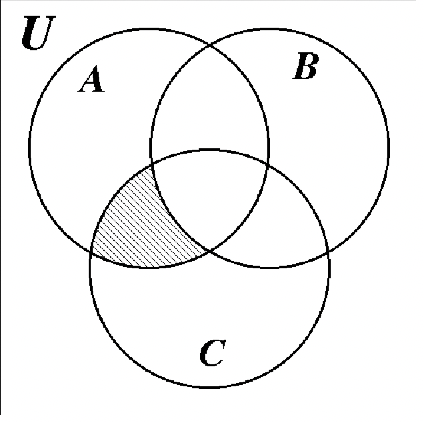 b. b. |
Enumere todos los subconjuntos posibles para cada conjunto dado.
| a. {} | b. {a} | c. {a, b} | d. {a, b, c} |
Sea A = {1, 2, 4}, B = {(a, c), 5} y C = {x}. Encuentra lo siguiente:
| a.\(A \times A\) | a.\(A \times B\) | c.\(B \times C\) |
| d.\(C \times A\) | a.\(C \times C\) |
Usa tus bloques A para hacer este problema. Que X representa el conjunto de círculos grandes e Y representa el conjunto de círculos rojos. Usando la notación de conjuntos y abreviaturas, encuentre lo siguiente:
| a. X - Y | b.\(\bf X \cap Y\) | c.\(\bf X \cup Y\) | d. Y - X |


