3.1: Definición y Propiedades
- Page ID
- 113206
Necesitarás: Monedas (Tarjeta de Material 1), A - Bloques (Tarjetas de Material 2A - 2E), Tiras Centémetros (Tarjetas de Material 17A - 17L)
Los números enteros están conformados por cero y los números de conteo 0, 1, 2, 3, 4, 5,. Comenzamos este conjunto de ejercicios explorando cómo sumar dos números enteros juntos. Para sumar 3 + 4, encontramos un conjunto con tres elementos y un conjunto diferente con cuatro elementos (no teniendo elementos en común con el primer conjunto). Combinamos los dos conjuntos y luego contamos cuántos elementos hay en la unión. Este método se ilustra en el siguiente ejercicio.
Saca el juego de 25 monedas de la Tarjeta de Material 1. Pon tres monedas en una mano y llama a este juego de monedas conjunto A. Pon cuatro monedas diferentes en tu otra mano y llama a este juego de monedas conjunto B. Usa la notación de conjunto apropiada y las abreviaturas de monedas al completar lo siguiente:
| a. A = | b. n (A) = |
| d. n (B) = | d. n (B) = |
Pon las monedas de ambas manos en una pila para formar la unión de A y B.
| e.\(A \cup B\) | f. n\(A \cup B\) |
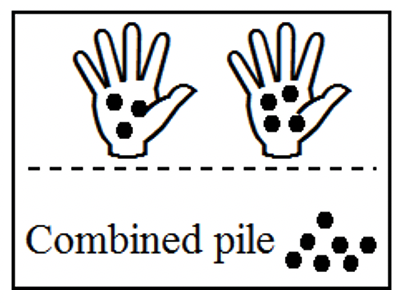
Entonces para sumar dos números, 3 y 4, debemos encontrar un conjunto A tal que n (A) = 3 y un conjunto B tal que n (B) = 4. Entonces, 3 + 4 es cuántos elementos hay en\(A \cup B\). En el Ejercicio 1, ya que n (\(A \cup B\)) = 7, luego 3 + 4 = 7. Por supuesto, ya lo sabíamos a partir de años de simulacro y práctica, flashcards, etc. a la derecha hay una imagen que muestra tres monedas en una mano y cuatro en otra. Combinando las monedas en un montón grande, se pueden contar para encontrar la suma.
Hay una restricción en los dos conjuntos elegidos que descubrirás haciendo el siguiente ejercicio.
Vamos a tratar de encontrar la respuesta a 3 + 6 usando el mismo método que acabamos de emplear. Pero esta vez, quiero que trabajes con conjuntos A y B como los defino aquí: A = {t, u, v} y B = {u, v, w, x, y, z}. Tenga en cuenta que n (A) = 3 y n (B) = 6.
| a. Enumerar los elementos en\(A \cup B\): |
| b. ¿Cuántos elementos hay en\(A \cup B\)? ____ |
| c. ¿3 + 6 = n\(A \cup B\)? ____ |
| d. ¿Es n (A) + n (B) = n\(A \cup B\)? ____ |
| e. ¿Cómo podrían elegirse los conjuntos A y B para que las respuestas tanto a c como a d fueran sí? Si necesitas una pista, ¡mira lo que está entre paréntesis en el párrafo inicial de este conjunto de ejercicios! |
Por cierto, ya que n (A) = 3 y n (B) = 6, ¡la parte c y d están haciendo la misma pregunta!
Usa tus A-Blocks para los siguientes ejercicios. Como recordatorio, la letra que está en tipo BOLD en cada palabra a continuación es la abreviatura utilizada para los nueve subconjuntos principales de A-Blocks. R ED, B LUE, G REEN, Y ELLOW, S MALL, L ARGE, C IRCLE, T RIANGLE, S Q UARE (Para denotar un bloque A en particular, use tres letras en el formato Tamaño, Color, Forma - por ejemplo, El triángulo azul grande es abreviado LBT, el cuadrado rojo pequeño se abrevia SRQ, etc.)
| a. Nombra dos subconjuntos de bloques A (cada uno con 6 elementos) que podrían usarse para encontrar la suma de 6 y 6: ____ y _____ |
| b. Ilustra cómo los dos conjuntos que elegiste darán la suma correcta al enumerar tanto los elementos en cada conjunto que nombraste como los elementos en la unión de los dos conjuntos (usando abreviaturas). ¡El número de elementos en el sindicato debería ser de 12! |
Ya que n (L) = 12 y n (T) = 8, vamos a averiguar si los subconjuntos de L y T se pueden utilizar para encontrar la suma de 12 y 8.
| a. Enumerar los elementos en (\(L \cup T\)): |
| b. n\(L \cup T\) = ____ |
| c. ¿Es n (\(L \cup T\)) igual a 12 + 8? ____ |
| d. ¿Por qué no funcionó usar los conjuntos de Bloques A Grandes y Bloques A Triangulares para encontrar la suma? |
Ahora sigue una definición formal y más general de adición de números enteros.
Teoría de Conjuntos Definición de Adición: Si A y B son dos conjuntos disjuntos, es decir\(A \cap B\) = Ø, entonces n (A) + n (B) = n (\(A \cup B\)).
A continuación se presentan algunos ejemplos de cómo utilizar la definición de adición de la teoría de conjuntos para agregar.
Utilice la definición de adición de la teoría de conjuntos para mostrar que 3 + 2 = 5.
Solución
Sea A = {x, y, z} y B = {m, r} Puesto que n (A) = 3, n (B) =2, y\(A \cap B\) = Ø entonces
| 3+2 = n (A) +n (B) | sustituyendo n (A) por 3 y n (B) por 2 |
| = n (\(A \cup B\)) | por la teoría de conjuntos definición de adición |
| = n ({x, y, z, m, r}) | por computación A |
| = 5 | contando los elementos en A |
Por lo tanto, 3 +2 = 5.
Utilice la definición de adición de la teoría de conjuntos para mostrar que 1 + 3 = 4
Solución
Dejar A = {x} y B {a, b, c}. Dado que n (A) = 1, n (B) = 3 y\(A \cup B\) = Ø, entonces
| 1 + 3 = n (A) + n (B) | sustituyendo n (A) por 1 y n (B) por 3 |
| = n (\(A \cup B\)) | por la teoría de conjuntos definición de adición |
| = n ({x, a, b, c}) | por computación\(A \cup B\) |
| = 4 | contando los elementos en\(A \cup B\) |
Por lo tanto, 1 + 3 = 4
Utilice la definición de suma de la teoría de conjuntos para mostrar que 0 + 4 = 4.
Solución
Dejar A = {} y B = {a, b, c, d}. Dado que n (A) = 0, n (B) = 4 y\(A \cup B\) = Ø, entonces
| 0 + 4 = n (A) + n (B) | sustituyendo n (A) por 0 y n (B) por 4 |
| = n (\(A \cup B\)) | por la teoría de conjuntos definición de adición |
| = n ({a, b, c, d}) | por computación\(A \cup B\) |
| = 4 | contando los elementos en\(A \cup B\) |
Por lo tanto, 0 + 4 = 4
La definición de adición nos permite verificar algunas propiedades sobre la adición. El ejemplo 3 verifica la propiedad de Set Theory que establece que para cualquier conjunto A,\(A \cup Ø\) = A.
Sea n (A) = a. ya que el número de elementos en el conjunto nulo es cero, entonces a + 0 = a y 0 + a = a.
Utilice la definición de adición de la teoría de conjuntos para hacer las siguientes adiciones. ¡Escríbelo a detalle! Sigue los ejemplos anteriores.
| a. mostrar que 2 + 4 = 6 |
| b. Demostrar que 2 + 2 = 4 |
| c. Mostrar que 3 + 0 = 3 |
Saca tu juego de Tiras Centémetros (Tiras en C). Hay doce tipos diferentes de tiras, cada una de las cuales tiene una longitud diferente. A continuación se muestra un listado de los diferentes tipos, con sus dimensiones, colores y las abreviaturas que usaremos para referirnos a cada uno. Aceptemos usar las abreviaturas en más de un contexto; una letra puede referirse a la tira física real en sí o podría referirse a la longitud de la tira. Esto no es exactamente perfecto en cuanto a notación, pero hará que el trabajo que sigue sea menos engorroso.
| 1 cm por 1 cm... W HITE... W |
| 1 cm por 2 cm... R ED... R |
| 1 cm por 3 cm... L IGERO VERDE... L |
| 1 cm por 4 cm... P URPLE... P |
| 1 cm por 5 cm... Y ELLOW... Y |
| 1 cm por 6 cm... D ARCA VERDE... D |
| 1 cm por 7 cm... BLAC K... K |
| 1 cm por 8 cm... CEJA N... N |
| 1 cm por 9 cm... B LUE... B |
| 1 cm por 10 cm... O GAMA... O |
| 1 cm por 11 cm... S ILVER... S |
| 1 cm por 12 cm... H OT ROSA... H |
Utilizaremos las Tiras en C para descubrir y reforzar conceptos y propiedades sobre la adición. Para muchos de los problemas, estaremos trabajando con “trenes”, que se hacen poniendo una o más tiras de extremo a extremo en línea recta. Por lo que el ancho permanecerá 1 cm pero la longitud del tren variará.
Para designar un tren que consta de más de una tira, escribimos un problema de adición para que primero se escriba la C-Strip de la izquierda y el resto, en su caso, se escriba de izquierda a derecha. A continuación, anote la forma en que se forman los trenes y cómo denotamos cada uno.
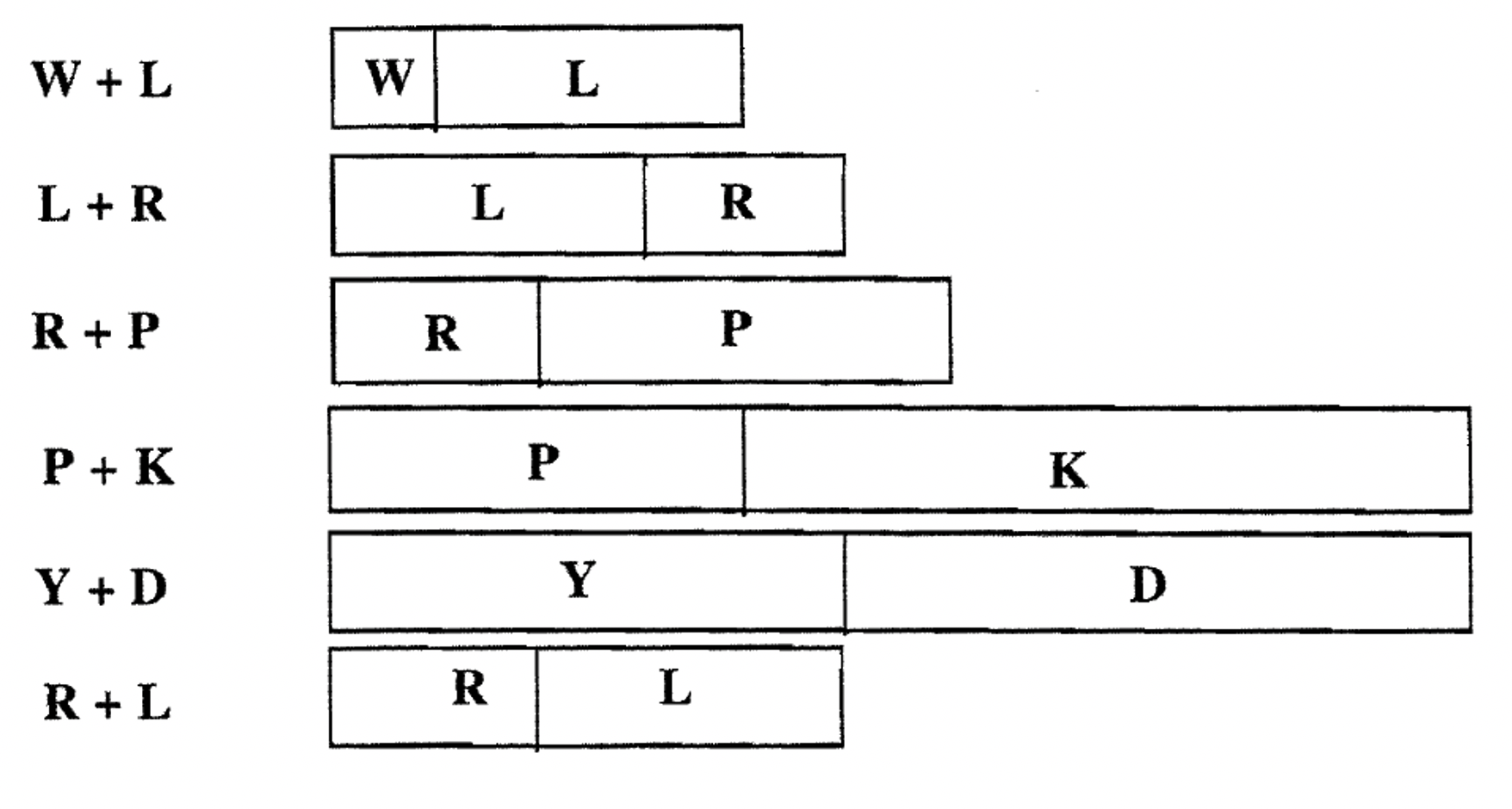
Usa las Tiras en C para hacer indicado el tren. Luego, encuentra una Tira en C de igual longitud y rellena cada pieza en blanco con la abreviatura de esa Tira en C
| a. P + L = | b. S + W = | c. R + K = |
| d. B + W = | e. N + L = | f. L + W = |
| g. P + Y = | h. D + R = | i. B + L = |
| j. Y + P = | k. R + D | l. L + B = |
| m. ¿Qué notas de j & g, k & h y l & i? |
Las partes j & g, k & h y l & i del Ejercicio 6 ilustran un principio importante sobre los números enteros llamado la Propiedad Conmutativa de la Adición.
La Propiedad Conmutativa de la Adición establece que si a y b son cualesquiera dos números enteros, entonces a + b = b + a.
Usando la definición de adición y este hecho importante de la Teoría de Conjuntos,
\(A \cup B = B \cup A\), podemos mostrar por qué la Propiedad Conmutativa de Adición es cierta:
a + b = n (A) + n (B) = n (\(A \cup B\)) = n (\(B \cup A\)) = n (B) + n (A) = b + a
La mayoría de nosotros llevamos años y años sumando números y así esta propiedad puede parecer obvia — es de segunda naturaleza que el orden en el que sumamos dos números sea irrelevante. Pero si aprovechas para preguntarle a un niño que apenas está aprendiendo a agregar las siguientes dos preguntas, incluso una justo después de la otra, puede notar que el niño puede hacer la primera de forma rápida y sencilla pero luego lucha un poco más en la segunda. Ese suele ser el caso si el niño aún no ha descubierto la propiedad conmutativa de adición. Como adultos, damos por sentado esta propiedad.
Primera pregunta: ¿Qué es 7 + 2? Segunda pregunta: ¿Qué es 2 + 7?
¿Cómo cree que un niño podría averiguar la respuesta a la primera pregunta y cómo podría averiguar cómo hacer la segunda pregunta? ¡Sea específico y asuma que las respuestas aún no se han memorizado! ¿Por qué podría percibirse la segunda pregunta como un problema más difícil?
Al sumar dos números juntos, algunas personas comienzan con el primer número y cuentan con el segundo número. Entonces, si piensas en 7 + 2, empieza con 7 y cuenta dos más en tu cabeza —ocho, nueve. Para 2 + 7, empieza con 2 y cuenta siete más en tu cabeza —tres, cuatro, cinco, seis, siete, ocho, nueve. Aunque la respuesta es la misma, 7 + 2 fue más rápido y más fácil de rastrear. ¡Solo piensa en la diferencia entre 1000 + 1 y 1 + 1000 usando este método de conteo! Gracias a Dios por la propiedad conmutativa de adición!
¿Y si tuvieras que sumar tres números juntos? En realidad, solo sumamos dos números juntos a la vez y luego sumamos el tercero a la suma de los dos primeros números. Utilizaremos tiras en C para ilustrar formas de sumar tres números juntos. Considera juntar las tiras C L, R y P para formar un tren. Calculemos la suma de estos tres de dos maneras distintas, trabajando primero entre paréntesis.
Rellene cada blanco con la abreviatura correcta de una C-Strip calculando primero la suma entre paréntesis y poniendo esa respuesta en el primer espacio en blanco. Después agrega una vez más para obtener la respuesta. Un ejemplo con números: (5 + 3) + 9 =\(\underline{8}\) + 9 =\(\underline{17}\).
El Ejercicio 8 ilustra otro principio importante sobre los números enteros llamado Propiedad Asociativa de la Adición.
La Propiedad Asociativa de la Adición establece que si a, b y c son tres números cualesquiera, entonces (a + b) + c = a + (b + c)
Usando la definición de suma y este hecho importante de la Teoría de Conjuntos\((A \cup B) \cup C = A \cup (B \cup C)\),, mostramos por qué la Propiedad Asociativa de la Adición es verdadera: (a + b) + c = (n (A) + n (B)) + n (C) = n (\(A \cup B\)) + n (C) = n ( \((A \cup B) \cup C\)) = n (\((A \cup B) \cup C\)= n (A) + n (\((B \cup C)\)) = n (A) + (n (B) + n (C)) = a + (b + c)
Utilizando el modelo del Ejercicio 8 y las Tiras en C, ilustrar otra aplicación de la propiedad asociativa de adición. Después anote una sentencia equivalente usando números.
La raíz en la palabra “asociativo” es asociado. Piense si el número medio se asociará con el primer número o el último número para el primer cálculo. En cuanto a sumar números en tu cabeza, puede ser mucho más fácil hacerlo de una manera en lugar de otra. Por ejemplo, para sumar 58 + 39 + 41, podrías pensar (58 + 39) + 41 = 97 + 41 = 138 o podrías pensar 58 + (39 + 41) = 58 + 80 = 138. 97 + 41 y 58 + 80 ambos equivalen a 138, pero eso no es obvio hasta después de agregar. Prefiero sumar primero los 39 y 41 juntos. La propiedad asociativa permite eso. Pero nuevamente, la propiedad asociativa es algo que la mayoría de los adultos dan por sentado y usan pero realmente no piensan en ello.
Aquí hay otro ejemplo. Si bien la suma de los tres números es la misma para cada problema, la forma de hacer los cálculos es diferente.
|
(84 + 56) + 73 140 + 73 213 |
84 + (56 + 73) 84 + 129 213 |
Haz un ejemplo propio mostrando una aplicación de la propiedad asociativa
Podría ser útil señalar que la propiedad conmutativa implica que ha habido un cambio de orden. Un cambio de orden significa que los números escritos están en un orden diferente. La propiedad asociativa implica que ha habido un cambio de paréntesis. Un cambio de paréntesis significa que hay diferentes números entre paréntesis y que los paréntesis están ahora alrededor de números diferentes.
Declarar qué propiedad (propiedad conmutativa o asociativa de suma) se está utilizando en cada ecuación. Pregúntate: ¿La diferencia entre el lado izquierdo y el lado derecho se debe al orden (propiedad conmutativa) o paréntesis (propiedad asociativa)?
| a. _____ | (99 + 76) + 38 = (76 + 99) + 38 |
| b. _____ | (65 + 22) + 56 = 56 + (65 + 22) |
| c. _____ | (57 + 88) + 43 = 57 + (88 + 43) |
| d. _____ | (a + b) + (c + d) = ((a + b) + c) + d |
Usamos las propiedades conmutativas y asociativas de la suma todo el tiempo para hacer aritmética simple; por supuesto, la aritmética podría no ser tan fácil si no se nos permitiera usar estas propiedades. Imagínese que ninguno de los bienes existía y la única manera de obtener la suma de tres números era sumarlos en orden de izquierda a derecha. Considera este problema aritmético: 17 + 59 + 83. Pasando de izquierda a derecha, primero sumamos 17 y 59 para obtener 76 y luego sumamos 83 a 76 para obtener la respuesta de 159. Bien, así que eso no es tan difícil. Pero se vuelve muy fácil si se nos permite usar las propiedades conmutativas y asociativas de adición como se muestra a continuación (se muestran tres formas usando diferentes pasos):
(17 + 59) + 83 = 83 + (17 + 59) Propiedad conmutativa
= (83 + 17) + 59 Propiedad asociativa
= 100 + 59
= 159
(17 + 59) + 83 = (59 + 17) + 83 Propiedad conmutativa
= 59 + (17 + 83) Propiedad asociativa
= 59 + 100
= 159
(17 + 59) + 83 = 17 + (59 + 83) Propiedad asociativa
= 17 + (83 + 59) Propiedad conmutativa
= (17 + 83) + 59 Propiedad asociativa
= 100 + 59
= 159
Por supuesto, la mayoría de nosotros probablemente automáticamente añadimos primero los 83 y 17 en nuestra cabeza sin molestarnos en pensar en las propiedades. Pero es por estas propiedades fundamentales que llegamos a la respuesta correcta sumando los números en cualquier orden o combinación que nos resulte conveniente.
Utilice las propiedades conmutativas y asociativas para agregar (135 + 384) + 165. Asume que prefieres sumar 135 y 165 en tu cabeza. Mostrar cada paso e indicar qué propiedad se está utilizando en cada paso. Entonces hazlo de nuevo de otra manera usando diferentes pasos.
Decimos que dos trenes son iguales si tienen la misma longitud. Por ejemplo, mira los seis trenes que se muestran a continuación. Todos estos tienen la misma longitud de 6 cm y así son todos iguales.
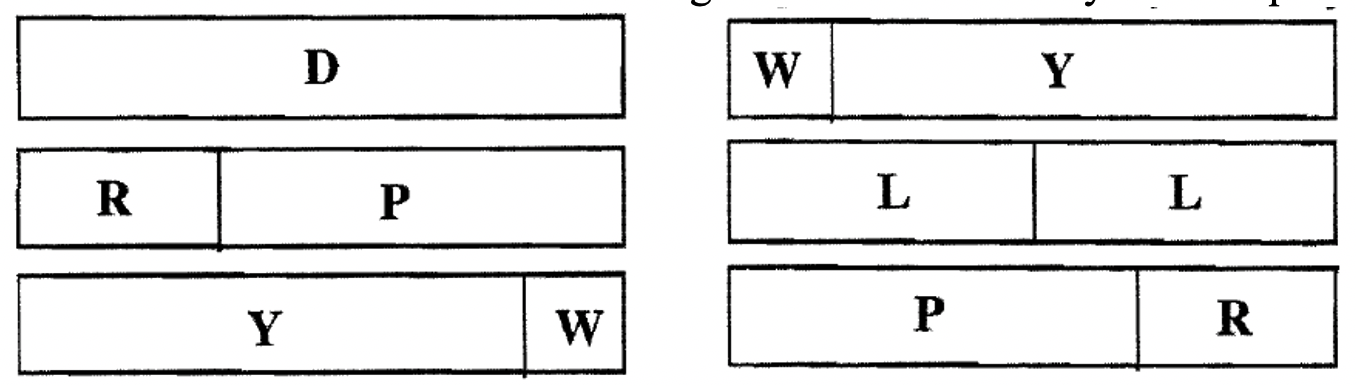
Si bien los seis trenes mostrados arriba son iguales, se consideran diferentes porque ninguno de ellos tiene exactamente las mismas franjas en exactamente el mismo orden. Aquí hay una lista de los seis trenes anteriores: D, W + Y, R + P, L + L, Y + W, P + R. Hay más trenes que tienen esta misma longitud pero diferentes a los enumerados hasta ahora. Por ejemplo, siete más son: W + R + R + W, W + P + W, P + W + W, W + W + P, W + L + W + W, R + L + W, L + W + W + W. De hecho, hay varios trenes más que tienen la misma longitud que el C-Strip Verde Oscuro que los 13 trenes diferentes enumerados hasta el momento. Todos los trenes listados se traducen en hechos adicionales sobre combinaciones de números que suman 6: W + Y = D se traduce a 1 + 5 = 6, W + P + W = D se traduce a 1 + 4 + 1 = 6, R + P = D se traduce a 2 + 4 =6, P + R = D se traduce a 4 + 2 = 6 y así sucesivamente.
Utilice las tiras C para enumerar todos los diferentes trenes que tienen la misma longitud que la tira C Verde Claro. Los diferentes trenes tienen diferentes tiras y/o un orden diferente de tiras.
Utilice los trenes que figuran en el Ejercicio 13 para escribir datos adicionales obtenidos sobre el número 3.
Use las tiras C para enumerar todos los diferentes trenes que tienen la misma longitud que la tira C Purple. Los diferentes trenes tienen diferentes tiras y/o un orden diferente de tiras.
Utilice los trenes enumerados en el Ejercicio 15 para escribir datos adicionales obtenidos sobre el número 4
Enumerar todos los diferentes trenes de igual longitud que el C-Strip Verde Oscuro es toda una tarea. Definiremos trenes equivalentes como trenes iguales que tienen la misma composición (mismas tiras exactas), pero las tiras están listadas en un orden diferente. Por ejemplo, W + R + L, W + L + R, L + R + W, L + W + R, R + L + W y R + W + L son todos trenes equivalentes porque cada uno está compuesto por una tira C roja, verde claro y blanca. W+L y L+W son trenes equivalentes porque todos están compuestos exactamente de las mismas tiras C: una tira C blanca y una tira en C roja. W+L, R+R, P, W+W+R y W+W+W+W son trenes iguales pero no equivalentes porque están compuestos por diferentes franjas. Los trenes no equivalentes son trenes iguales compuestos por diferentes tiras C. Si están compuestas por las mismas tiras en C pero están en un orden diferente, ¡son equivalentes!
Enumere todos los trenes no equivalentes (anote la última frase en negrita en el párrafo anterior) de igual longitud que la Franja C Verde Oscuro. Eso significa que solo uno de los seis enumerados en la mitad del párrafo anterior (y no importa cuál) debe ser anotado en esta lista. Recuerda incluir el tren de una sola tira. ¿Cuántos trenes no equivalentes de longitud a Dark Green C-Strip hay?
De tu trabajo en el Ejercicio 17, haz una lista de todos los datos sobre qué combinaciones de números suman 6.
Si nos fijamos en las C-Sstrips, es claro que algunas son más largas que otras. Decimos que una C-Strip es más larga que otra C-Strip si hay una C-Strip que se puede agregar a la segunda C-Strip para hacer un tren igual en longitud a la C-Strip más larga. Por ejemplo, la C-Strip Negra es más larga que la Purple C-Strip porque podemos agregar la C-Strip Verde Claro a la Tira en C Púrpura para hacer un tren igual en longitud a la C-Strip Negra. Escribimos K es más largo que P porque K = P +\(\bf \underline{\text{L}}\).
Verifique que cada una de las tiras en C nombradas sea más larga que la otra tira C rellenando las piezas en blanco. Se utilizan abreviaturas.
| a. H es más largo que O porque H = O + ___ |
| b. N es más largo que L porque N = L + ___ |
| c. B es más largo que W porque B = W + ___ |
| d. P es más largo que R porque P = R + ___ |
| e. S es más largo que K porque S = K + ___ |
| f. D es más larga que Y porque D = Y + ___ |
El mismo principio que se acaba de usar con las Tiras C se aplica al comparar dos números enteros.
Definición: El número entero m es mayor que el número entero n si hay un número entero k tal que m = n + k.
En matemáticas, el símbolo utilizado para denotar “es mayor que” es: ">”. Por lo tanto, "7 > 5" se lee “Siete es mayor que cinco”.
El ejercicio 19 se puede modificar para expresar información sobre los números. Por ejemplo, la parte a corresponde al hecho de “12 es mayor que 10 porque 12 = 10 + 2" o si queremos escribirla simbólicamente, escribimos “12 > 10 porque 12 = 10 + 2".
Verifica cada uno de los siguientes (he hecho la parte a por ti):
| a. 9 > 3 porque\(\underline{9 = 3 + 6}\) | b. 30 > 22 porque ____ |
| c. 156 > 96 porque ____ | d. 80 > 0 porque ____ |
| e. 231 > 195 porque ____ | f. 987> 967 porque ____ |
Ahora que has trabajado un poco con mayor que, bien podemos definir menos de.
Definición: El número entero r es menor que el número entero s si hay un número entero k tal que r + k = s.
En matemáticas, el símbolo utilizado para denotar “es menor que” es: "<”. Por lo tanto, "4 < 9" se lee “Cuatro es menos de nueve”.
Verifica cada uno de los siguientes (he hecho la parte a por ti):
| a. 9 < 22 porque\(\underline{9 + 13 = 22}\) | b. 30 < 99 porque |
| c. 19 < 70 porque | d. 0 < 32 porque |
| e. 489 < 500 porque | f. 65 < 201 porque |
“Menos que” y “mayor que” se pueden usar para ordenar números en una línea numérica. Rellene cada pieza en blanco con la derecha o la izquierda.
| a. Si m < n, entonces m es al _____________ de n en la recta numérica |
| b. Si m > n, entonces m es al _____________ de n en la recta numérica. |
Formar dos trenes de Tiras C, m y n, que sean iguales. Si p es una C-Strip o tren de C-Tiras de cualquier longitud, ¿siempre es cierto que m + p = n + p?
Tome dos Tiras C diferentes o forme un tren de Tiras en C,\(m\) y\(n\), tal que\(m > n\). Si p es una C-Strip o tren de C-Sstrips de cualquier longitud, ¿siempre es cierto que\(m + p > n + p\)?
El ejercicio 23 ilustra que la propiedad aditiva de la igualdad. Si se agrega el mismo número a ambos lados de una igualdad, la ecuación sigue siendo verdadera. El ejercicio 24 ilustra la propiedad aditiva de la desigualdad. Si se suma el mismo número a ambos lados de una desigualdad, la desigualdad sigue siendo cierta.
Si tomas cualquiera de dos trenes, s y t, y los mides colocando uno al lado del otro, notarás que o son de igual longitud o uno de ellos es más largo que el otro. Esta observación nos lleva a la ley de la tricotomía.
Si a y b son números enteros, entonces exactamente uno de los siguientes es verdadero: a = b o a < b or a > b.
Coloque el símbolo correcto (<, =, or >) entre cada par de números. Verifica si tienes razón si usas el símbolo menor o mayor que (como en los ejercicios 20 y 21).
| a. 8 ____ 19 ____ |
| b. 24 ____ 13 ____ |
Iniciamos este ejercicio establecido definiendo los números enteros. Usando la notación de conjunto, exprese los números enteros usando el método de listado: ____
Si se suman dos números enteros, ¿la suma siempre será un número entero? ____
Si se suman dos números enteros, ¿es posible obtener más de una respuesta? ____
Tus respuestas a los Ejercicios 24 y 25 deben confirmar que la suma de dos números enteros es siempre un número entero único. A esto se le llama la propiedad de cierre de suma para números enteros. Decimos que el conjunto de números enteros está cerrado bajo suma porque cuando se suman dos números enteros cualesquiera juntos, se obtiene otro número entero único.
Un conjunto se cierra bajo suma si la suma de dos elementos cualesquiera en el conjunto (estos podrían ser los mismos elementos o dos elementos diferentes) produce un elemento único en el mismo conjunto.
La adición es en realidad solo una operación que realizamos en dos miembros de un conjunto. Otras operaciones con las que sin duda conoces son la resta, la multiplicación y la división. Hay otras operaciones y hay otras nuevas que puedes inventar, pero dejaremos esa discusión para otro momento. Si la operación se define para ser realizada en exactamente dos elementos, entonces se llama una operación binaria.
En general, un conjunto se cierra bajo una operación si cuando se realiza la operación en dos elementos cualesquiera del conjunto, la respuesta es un elemento único del mismo conjunto.
Para mostrar que un conjunto no está cerrado bajo suma, debes dar un contraejemplo que muestre que cuando agregas dos números en el conjunto, obtienes una suma que no está en el conjunto. Los dos números que elijas pueden ser el mismo número o números diferentes.
¿El conjunto {1, 2, 3, 4, 5} está cerrado bajo adición?
Solución
Imagina que tenías dos sombreros, cada uno conteniendo estos cinco números en el set escrito en trozos de papel. Entonces cada sombrero contiene el conjunto {1, 2, 3, 4, 5}. Si sacas un número de cada sombrero, podrías obtener el mismo número dos veces o podrías obtener números diferentes. Algunas de las sumas son 1 + 1 = 2, 2 + 3 = 5, 1 + 3 = 4, 3 + 3 = 6, etc. Obsérvese que las tres primeras sumas 2, 5 y 4 están en el conjunto {1, 2, 3, 4, 5}. Pero para que un conjunto se cierre, la suma de cada dos números posibles en el conjunto debe arrojar un número en el conjunto original. Dado que 3 + 3 = 6, (donde los dos agregados, 3 y 3, están en el conjunto original, pero la suma 6 NO está en el conjunto original), entonces el conjunto {1, 2, 3, 4, 5} no está cerrado. Hay cualquier número de contraejemplos que puedas usar para mostrar que no está cerrado. 3 + 3 = 6 servirá. O alguien más podría escribir 4 + 5 = 9. ¿Cuáles son otros dos contraejemplos que podrías usar para mostrar que {1, 2, 3, 4, 5} no se cierra bajo suma?
¿Se cierra {4} por adición?
Solución
La única posibilidad de probar es 4 + 4, que es 8, y 8 no está en el set. Por lo que el conjunto no está cerrado. El contraejemplo para mostrar que no está cerrado es 4 + 4 = 8.
¿Está {5, 10, 15, 20,.} cerrado por adición?
Solución
Comience probando algunos ejemplos: 5 + 5 = 10 que está en el conjunto; 10 + 15 = 25 que está en el conjunto (observe los tres puntos lo que significa que los siguientes números son 25, 30 y 35. Parece que está cerrado. Pero, ¿cómo puedes convencer a alguien de que la suma de dos números cualesquiera en el set siempre estará en el set original? Tenga en cuenta que el conjunto está compuesto por múltiplos de 5. Tenga en cuenta que dos múltiplos cualesquiera de 5 se pueden escribir como 5 veces algo, como 5x y 5y. Que 5x y 5y denoten dos elementos arbitrarios en el conjunto original. Sumándolos juntos, obtenemos 5x + 5y = 5 (x+y) que es otro múltiplo de 5 (ya que es 5 veces algo). Entonces, debes estar convencido de que la suma de dos elementos cualesquiera en el conjunto es un múltiplo de 5, que es en lo que consistía el conjunto original. Por lo tanto, {5, 10, 15, 20,.} se cierra bajo adición.
Indique si cada conjunto a continuación está cerrado por adición o no. Si no está cerrado, proporcione un contraejemplo que muestre dos elementos en el conjunto cuya suma no esté en el conjunto. En general, proporcionar un ejemplo que demuestre que algo no siempre es cierto se llama proporcionar un contraejemplo. Si un conjunto está cerrado, demuestre y explique por qué.
| a. {0} |
| b. {1} |
| c. {0,2,4,6,..} |
| d. {1,3,5,7,..} |


