4.1: Definición y Propiedades
- Page ID
- 113214
Este conjunto de ejercicios presenta una manera diferente y desafiante para que veas la multiplicación. Utilizarás las Tiras Centémetros (Tiras en C) para explorar y descubrir las propiedades conmutativas, asociativas y distributivas de la multiplicación. A continuación se muestra un recordatorio de las diferentes C-Sstrips con las que trabajaremos junto con la abreviatura utilizada para cada una resaltada en negrita:
| 1 cm por 1 cm | W HITE | 1 cm por 2 cm | R ED |
| 1 cm por 3 cm | L VERDE CICHO | 1 cm por 4 cm | P URPLE |
| 1 cm por 5 cm | AMARILLO | 1 cm por 6 cm | D ARCA VERDE |
| 1 cm por 7 cm | BLAC K | 1 cm por 8 cm | CEJAS N |
| 1 cm por 9 cm | B LUE | 1 cm por 10 cm | GAMA O |
| 1 cm por 11 cm | S ILVER | 1 cm por 12 cm | ROSA INTENSO |
Comenzaremos definiendo una forma de “multiplicar” dos tiras en C juntas. Considera multiplicar la tira C Púrpura por la Tira en C Amarilla. Usando abreviaturas, escribiremos\(P \times Y\), que leeremos en voz alta como “P cruz Y”. El primer paso en esta “multiplicación” es colocar la primera tira (P) hacia abajo en posición horizontal y luego colocar la segunda tira (Y) debajo de la primera tira para que quede perpendicular a la primera tira. El segundo paso es rellenar más tiras en C amarillas junto a la que ya está ahí para que formes un rectángulo de tiras amarillas donde la longitud es la tira amarilla y el ancho es la franja morada. Por último, retire la tira horizontal (púrpura en este caso) y forme un tren de la (s) franja (s) vertical (amarilla en este caso). Este tren es\(P \times Y\) y se muestra a continuación. Vea las ilustraciones de los tres pasos.
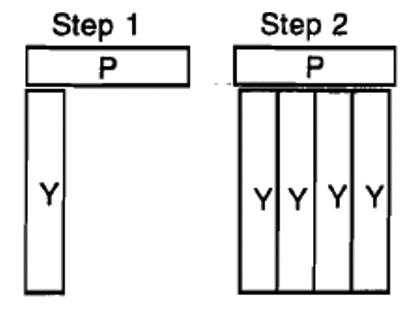

Decimos que\(P \times Y\) es el tren que consta de 4 tiras en C amarillas. Es importante notar que la respuesta es un tren que se forma con sólo franjas amarillas, que es la segunda letra en la multiplicación.
a. hacer el tren\(P \times Y\) como se explicó anteriormente. Guardarla hasta terminar la parte d.
b. encontrar\(Y \times P\) siguiendo el mismo procedimiento utilizado para encontrar\(P \times Y\), haciendo los dos primeros pasos y mostrándolos a continuación.
| Paso 1: | Paso 2: |
c. Este tren con el que eventualmente termines debe consistir solo en tiras C moradas. ¿Cuántas tiras moradas hay? Dibuja una imagen del tren\(Y \times P\).
d. Colocar los dos trenes,\(P \times Y\) y\(Y \times P\), uno al lado del otro y comparar las longitudes de los dos trenes. ¿Qué notas?
Para simplificar la notación, aceptemos decir que dos trenes son iguales si tienen la misma longitud. En otras palabras, de lo que descubriste en el Ejercicio 1,\(P \times Y = Y \times P\).
Para los siguientes ejercicios, describa los trenes formados haciendo las siguientes multiplicaciones con tiras C. Se debe formar físicamente cada tren pasando por los mismos pasos utilizados para multiplicar\(P \times Y\) en la página anterior. Para las partes a y b, rellene la primera pieza en blanco con un número (cuántos) y la segunda pieza en blanco con un color. Guarda cada tren para responder a la parte c. Usa tu observación para escribir las ecuaciones solicitadas en el Ejercicio 1d. Por ejemplo, desde que descubriste\(P \times Y = Y \times P\), esto se traduce en\(4 \times 5 = 5 \times 4\), ya que P tiene 4 cm de largo e Y es de 5 cm de largo. Usa este ejemplo para rellenar espacios en blanco para los ejercicios 2, 3 y 4.
Encontrar\(P \times Y\). Este tren consta de
Encontrar\(Y \times P\). Este tren consta de
a. Encontrar\(R \times D\). Este tren consta de _____ tiras en C
b. Encontrar\(D \times R\). Este tren consta de ______ tiras en C
c.\(R \times D\) se compone de ____ tiras blancas y\(D \times R\) se compone de _____ tiras blancas.
d. ¿Qué nota al comparar las longitudes de los trenes\(R \times D\) y\(D \times R\)?
e. de su trabajo en las partes a - d, escriba una ecuación que incluya las tiras C R y D; luego traduzca la ecuación a una con números.
a. Encontrar\(K \times L\). Este tren consta de _____ tiras en C
b. Encontrar\(L \times K\). Este tren consta de _____ tiras en C
c.\(K \times L\) se compone de ____ tiras blancas y\(L \times K\) se compone de _____ tiras blancas.
d. ¿Qué nota al comparar las longitudes de los trenes\(K \times L\) y\(L \times K\)?
e. de su trabajo en las partes a - d, escriba una ecuación que incluya las tiras C K y L; luego traduzca la ecuación a una con números.
a. Encontrar\(H \times W\). Este tren consta de _____ tiras en C
b. Encontrar\(W \times H\). Este tren consta de _____ tiras en C
c.\(H \times W\) se compone de ____ tiras blancas y\(W \times H\) se compone de ____ tiras blancas.
d. ¿Qué nota al comparar las longitudes de los trenes\(H \times W\) y\(W \times H\)?
e. de su trabajo en las partes a - d, escriba una ecuación que incluya las tiras C H y W; luego traduzca la ecuación a una con números.
Los problemas anteriores ilustran la propiedad conmutativa de la multiplicación para los trenes.
La propiedad conmutativa de multiplicación para trenes establece que si s y t son dos trenes cualesquiera, entonces\(s \times t = t \times s\)
Nota: Un tren puede consistir en una o más tiras C. En otras palabras, una sola tira C blanca (o de cualquier otro color) es en realidad un tren. ¡No tiene que haber un vagón de vagón y motor!
Rellene los espacios en blanco a cada uno de los siguientes problemas. Para ello, toma la tira c de color que se muestra después del signo de multiplicación y haz un tren de ese color que sea igual en longitud a la tira c del lado derecho del signo igual. Segundo, toma el tren y conviértelo en un rectángulo. Luego encuentra una tira en C que se ajuste a lo ancho del rectángulo. Escribe la abreviatura de esa tira en forma de C en el espacio en blanco.
| a. ____\(\times R = H\) | b. ____\(\times P = P\) | c. ____\(\times L = D\) |
| d. ____\(\times R = N\) | e. ____\(\times L = B\) | f. ____\(\times W = K\) |
| g. ____\(\times R = D\) | h. ____\(\times D = H\) | i. ____\(\times Y = O\) |
a. Saque la tira en C Hot Pink (H). Usa tus tiras C (de un color a la vez) para ver si puedes formar un tren compuesto por tiras en C del mismo color igual en longitud a la tira c rosa fuerte en otras palabras, mira si puedes hacerlo con todos los blancos (siempre posible para cualquier tren), o todos los rojos, o todos los verdes claros, etc. Deberías poder hacer seis diferentes trenes cada tren se compone de un solo color. Dibuja una imagen de cada uno de estos trenes bajo el Hot Pink que se muestra. He dibujado dos trenes para ti ya uno es simplemente la tira rosa fuerte (un tren que consiste en solo una tira c), y un segundo está compuesto por tres tiras en c moradas.
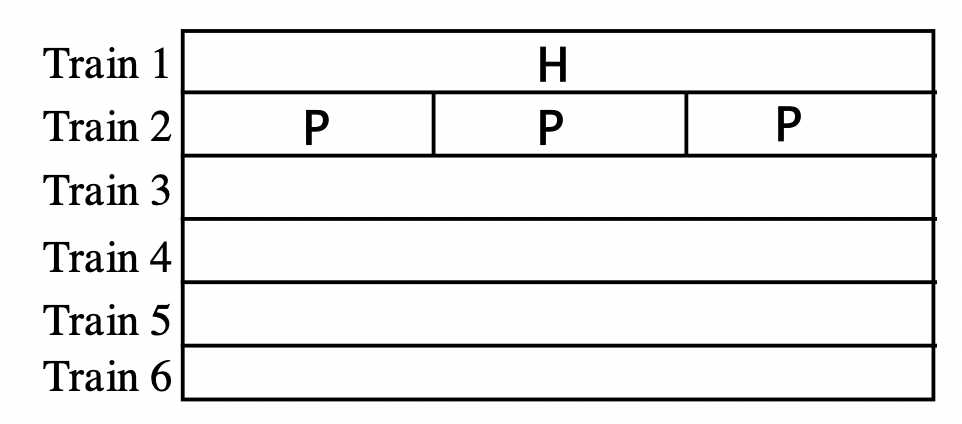
b. Su trabajo del ejercicio 5 debería ayudar a completar este ejercicio. Toma cada tren, uno a la vez, y coloca cada tira en posición vertical, pero lado a lado para formar un rectángulo. Luego, encuentra una tira en C que se ajuste a lo ancho (o parte superior) del rectángulo. Esto debería indicarte a partir de qué problema de multiplicación se formó cada tren. Escribe una ecuación usando tiras en C y luego traduce a una ecuación con números. Por ejemplo, para el tren 2, primero haría un rectángulo con las tres tiras en C moradas. A continuación, trataría de encontrar una tira en C para que quepa en la parte superior, que sería de color verde claro. Por lo tanto, el tren 2 se formó a partir de la multiplicación\(L \times P\) recuerde que dado que el tren se forma con tiras en C moradas, P es la segunda letra en la multiplicación. Entonces, la ecuación en c-strips es\(L \times P = H\), y el equivalente numérico es\(3 \times 4 = 12\). Siga este mismo procedimiento para los otros cuatro trenes que realizó en la parte a.
Tren 1 ilustra la multiplicación\(W \times H = H\), o\(1 \times 12 = 12\). (Tenga en cuenta que si la tira de color rosa intenso es vertical, la tira en C blanca se ajusta en la parte superior).
Tren 2 ilustra la multiplicación\(L \times P\) = H, o\(3 \times 4 = 12\)
Tren 3 ilustra la multiplicación ____\(\times\) ____ = H, o ____\(\times\) ____ = 12
El tren 4 ilustra la multiplicación ____\(\times\) ____ = H, o ____\(\times\) ____ = _____
El tren 5 ilustra la multiplicación ____\(\times\) ____ = H, o ____\(\times\) ____ = _____
El tren 6 ilustra la multiplicación ____\(\times\) ____ = H, o ____\(\times\) ____ = _____
Para el tren 2 en el ejercicio 6, hice un tren de tiras en C moradas iguales en longitud a la tira c rosa fuerte. Ahora, haz un tren de tiras en C moradas iguales en longitud a la tira c marrón (N). Toma el tren de las tiras en C moradas y conviértelo en un rectángulo.
¿Qué color de tira en C mide a lo largo del ancho de este rectángulo? ______
Ponga la respuesta (abreviatura de la tira c) en el espacio en blanco para resolver la multiplicación: ____\(\times\) P = N.
Ahora, exploraremos más sobre las ecuaciones formadas en el ejercicio 5. Considera la parte A. Debiste haber escrito\(D \times R = H\). Esto es análogo al enunciado\(6 \times 2 = 12\). Pero, si realmente miras el tren original que se formó para encontrar la respuesta, verías que había 6 tiras en C rojas que hacían un tren igual en longitud a la tira en c rosa fuerte. Esto da lugar a una de las definiciones de número entero de multiplicación. La multiplicación es realmente lo mismo que la suma repetida.
Si a y b son números enteros, entonces a\(\times\) b = b + b+ b+ b +... + b, donde hay a adiciones de b en esta suma.
Me gusta pensar en usar la definición así:
3\(\times\) 4 significa 3 cuatro patas agregadas juntas o 3\(\times\) 4 = 4 + 4 = 12
4\(\times\) 3 significa 4 tres agregados juntos, o 4\(\times\) 3 = 3 + 3 + 3 + 3 = 12
5\(\times\) 2 significa 5 dos agregados juntos, o 5\(\times\) 2 = 2 + 2 + 2 + 2 + 2 = 10
2\(\times\) 5 significa 2 cincos sumados juntos, o 2\(\times\) 5 = 5 + 5 = 10
Tenga en cuenta que aunque 3\(\times\) 4 da la misma respuesta que 4\(\times\) 3, ¡no significa lo mismo! Uno significa 4 + 4 + 4 y el otro significa 3 + 3 + 3 + 3 + 3. Antes de profundizar en esta discusión, quiero que usen la definición de adición repetida para calcular lo siguiente:
Utilice la definición de adición repetida de multiplicación para calcular lo siguiente. Primero, escribe el significado de la multiplicación, y luego computa la respuesta.
a. 6\(\times\) 3 =
b. 2\(\times\) 9 =
c. 9\(\times\) 2 =
Ahora bien, puede parecerle obvio que 3\(\times\) 4 es la misma respuesta que 4\(\times\) 3. Eso es porque sin duda llevas años usando la propiedad conmutativa de adición. Si realmente pensaste o no por qué era verdad es otra cosa. Pero, aunque 3\(\times\) 4 da la misma respuesta que 4\(\times\) 3, no significa lo mismo. Uno significa 4 + 4 + 4 y el otro significa 3 + 3 + 3 + 3 + 3. A un niño que apenas se está enterando de la suma y la multiplicación, no hay razón para que concluya que una suma (4 + 4 + 4) pasa a dar la misma respuesta que la otra suma (3 + 3 + 3 + 3). Por ejemplo, si me pidieran que computara las dos sumas siguientes, no me resultaría evidente en absoluto que la respuesta a cada uno sería terminar siendo la misma:
| 17 + 17 + 17 + 17 y 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 |
En realidad, me parece bastante asombroso que sean iguales. Pero, efectivamente lo son, porque la primera suma proviene del problema de multiplicación 4\(\times\) 17 (ya que hay 4 diecisiete sumados), y la segunda suma proviene del problema de multiplicación 17\(\times\) 4 (ya que hay 17 cuatros sumados). Posteriormente, cuando discutimos una definición más geométrica para la multiplicación, se hace evidente por qué la propiedad conmutativa de la multiplicación es verdadera.
La propiedad conmutativa de la multiplicación para números enteros establece que si a y b son dos números cualesquiera, entonces
\[a \times b = b \times a. \nonumber \]
Entonces, lo muy emocionante de la propiedad conmutativa de la multiplicación es que, dado un problema como 100\(\times\) 7, donde tardaría mucho en escribir y calcular la respuesta usando la estricta definición de multiplicación agregando 7 una y otra vez, podemos usar nuestro conocimiento de la propiedad conmutativa, es decir 100\(\times\) 7 = 7\(\times\) 100, y computar la segunda multiplicación en su lugar. ¿No estaría de acuerdo en que 100 + 100 + 100 + 100 + 100 + 100 es más rápido y más fácil de calcular que sumar 100 sietes? Gracias a Dios por la propiedad conmutativa de la multiplicación!!!
Antes de pasar a otra propiedad, practiquemos verificar que la propiedad conmutativa de la multiplicación es cierta para algunos números usando la definición de adición repetida de multiplicación. La propiedad conmutativa requiere de dos números (no tienen que ser dos números diferentes) y hay dos lados de una ecuación para verificar. La diferencia entre las expresiones a\(\times\) b y b\(\times\) a es que el orden de los números es diferente. Recuerde que la propiedad conmutativa significa que ha habido un cambio de orden. Para verificar la propiedad conmutativa de la multiplicación, es necesario utilizar la definición de adición repetida de multiplicación y agregar de izquierda a derecha, un número a la vez. El siguiente ejemplo muestra cómo verificar la propiedad conmutativa de la multiplicación, dado un conjunto de dos números.
Verificar que la propiedad conmutativa de la multiplicación sea verdadera para el conjunto de números dado. Tendrás que recordar cómo sumar en base seis para hacer la parte b.
a. {5, 3}
Solución
Tengo que mostrarme\(5 \times 3 = 3 \times 5\). Desde\(5 \times 3\) = 3 + 3 + 3 + 3 + 3 = 6 + 3 + 3 + 3 = 9 + 3 + 3 = 12 + 3 = 15 y desde\(3 \times 5\) = 5 + 5 + 5 = 10 + 5 = 15, entonces\(5 \times 3 = 3 \times 5\), porque ambos son iguales a 15.
b. {\(3_{\text{six}}, 4_{\text{six}}\)}
Solución
Necesito mostrar\(3_{\text{six}} \times 4_{\text{six}} = 4_{\text{six}} \times 3_{\text{six}}\) Desde\(3_{\text{six}} \times 4_{\text{six}} = 4_{\text{six}} + 4_{\text{six}} + 4_{\text{six}} = 12_{\text{six}} + 4_{\text{six}} = 20_{\text{six}}\) y desde\(4_{\text{six}} \times 3_{\text{six}} = 3_{\text{six}} + 3_{\text{six}} + 3_{\text{six}} + 3_{\text{six}} = 10_{\text{six}} + 3_{\text{six}} + 3_{\text{six}} = 13_{\text{six}} + 3_{\text{six}} = 20_{\text{six}}\), entonces\(3_{\text{six}} \times 4_{\text{six}} = 4_{\text{six}} \times 3_{\text{six}}\), porque ambos iguales\(20_{\text{six}}\).
Verificar la propiedad conmutativa de la multiplicación escribiendo una ecuación que debe ser verdadera y usando la definición de adición repetida de multiplicación es verdadera usando el conjunto de números dado. Simplifica cada expresión por separado; luego muestra que son iguales.
| a. {4, 3} |
| b. {\(2_{\text{five}}\),\(3_{\text{five}}\)} |
| c. Conformar un conjunto en una base distinta a 10 y verificar la propiedad conmutativa de la multiplicación. |
También podemos usar la definición de adición repetida de multiplicación para multiplicar en otros sistemas de numeración. Estudiar los siguientes ejemplos y luego trabajar a través de los problemas en el ejercicio 10.
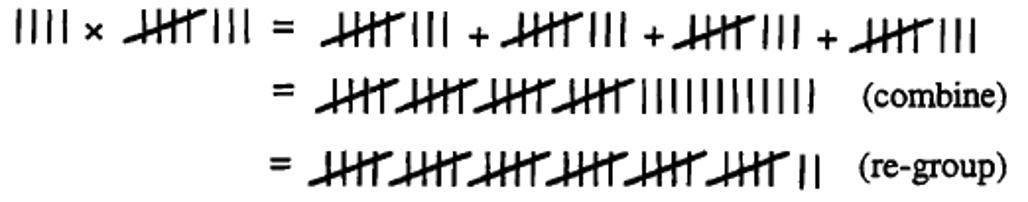
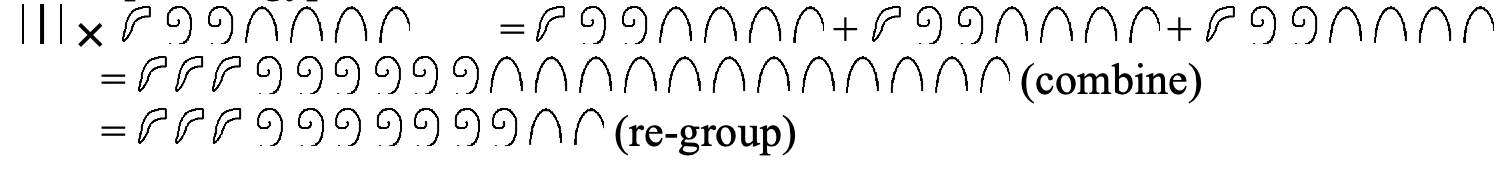
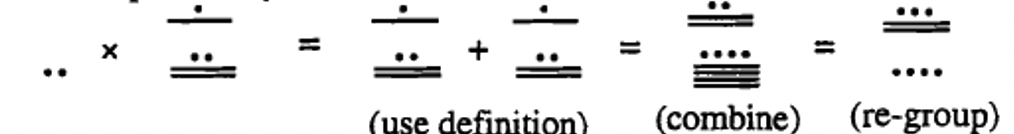
Observe que todos estos ejemplos se hacen completamente en el sistema de numeración dado. Todos los pasos se muestran en ese sistema de numeración. Así es como debes hacer los problemas en el ejercicio 10. Si lo desea, puede verificar la respuesta después de completar el problema convirtiéndolo a base diez. Por ejemplo, el ejemplo maya en base diez es 2\(\times\) 132. Entonces la respuesta debería ser 264. Si conviertes la respuesta final a base diez, también es 264.
Utilice la definición de adición repetida de multiplicación para calcular lo siguiente. Asegúrese de escribir el significado de la multiplicación en el sistema dado (ver ejemplos en la página anterior), mostrando todo el trabajo e intercambios (si es necesario), para calcular la respuesta. No hagas el problema en base diez, aunque puedes usar la base diez para verificar la respuesta cuando termines.
|
a. 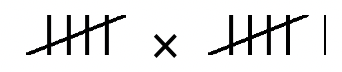 |
|
b. 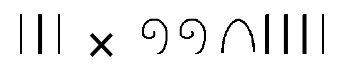 |
|
c. 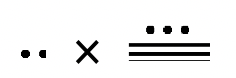 |
A continuación, formaremos los trenes para\((R \times L) \times P\) y para\(R \times (L \times P)\). Sólo podemos trabajar en uno a la vez. En ambos casos, primero debes hacer lo que hay dentro de los paréntesis.
a. primero, vamos a hacer\((R \times L) \times P\). Comience formando el tren\(R \times L\) para usar en la parte b.
b. A continuación, necesitamos formar el tren\((R \times L) \times P\). La primera parte\(R \times L\), que formaste en la parte a, debe estar en posición horizontal, y la tira en c púrpura va por debajo de ella, perpendicular al tren\(R \times L\). Tenga en cuenta que aunque\(R \times L\) se compone de más de una tira en C, todavía forma un tren a través de la parte superior. En el espacio de la derecha, dibuje una imagen de cómo se ve esto hasta ahora.
c. Hacer la multiplicación rellenando el resto de las tiras en C moradas en la posición vertical debajo del tren\(R \times L\); luego formar un tren a partir del rectángulo de tiras en C moradas. Conserva este tren hasta que hayas terminado todo el ejercicio 11. ¿Cuántas tiras en C moradas hay en el tren formadas al hacer la multiplicación\((R \times L) \times P\)?
d. Ahora, vamos a hacer\(R \times (L \times P)\). Comience formando el tren\(L \times P\) para usar en la parte e.
e. A continuación, formar el tren\(R \times (L \times P)\). Poner la primera parte, R, en la posición horizontal. La segunda parte\(L \times P\), formada en la parte d, debe ir en posición vertical como un tren largo, por debajo y perpendicular al tren R. No separar las franjas moradas en\(L \times P\) línea como un tren vertical largo (compuesto por más de una tira C púrpura) debajo de la tira en c roja. A la derecha, dibuje una imagen de cómo se ve esto hasta ahora.
f. hacer la multiplicación rellenando el resto de las tiras en C moradas para formar el rectángulo; luego hacer un tren con el rectángulo de tiras en C moradas. ¿Cuántas tiras en C moradas hay en el tren formadas al hacer la multiplicación\(R \times (L \times P)\)?
g. Compara la longitud del tren\((R \times L) \times P\), de la parte c con la longitud del tren\(R \times (L \times P)\), de la parte f. ¿Qué notas?
h. A partir de su observación, escriba una ecuación usando las tiras en C:
i. Traducir la ecuación de la parte h a una con números:
j. Escribe el lado izquierdo de la ecuación que escribiste en la parte i (que tiene números, no tiras C), y simplifica siguiendo el orden de las operaciones haz primero lo que está entre paréntesis. Entonces, haz lo mismo para el lado derecho de la ecuación.
Lado izquierdo:
Lado derecho:
k. ¿Son iguales las dos expresiones que simplificaste en la parte (j)? Si es así, has verificado que la ecuación de la parte (i) es verdadera
A continuación, formaremos los trenes para (\(Y \times R) \times L\)y para\(Y \times (R \times L)\).
a. primero, haremos (\(Y \times R) \times L\). Comience por formar el tren\(Y \times R\).
b. A continuación, necesitamos formar el tren (\(Y \times R) \times L\). La primera parte\(Y \times R\), que formaste en la parte a, debe estar en posición horizontal, y la tira en C verde claro debe ir por debajo de ella, perpendicular al tren\(Y \times R\). Tenga en cuenta que aunque\(Y \times R\) se compone de más de una tira en C, todavía forma un tren que se encuentra a través de la parte superior. Eso está bien. A continuación, dibuje una imagen de cómo se ve esto hasta ahora.
c. Hacer la multiplicación rellenando el resto de las tiras en C de color verde claro y luego haciendo un tren con el rectángulo de tiras en C de color verde claro. Conserva este tren hasta que hayas terminado todo el ejercicio 12. ¿Cuántas tiras en C de color verde claro hay en el tren formadas al hacer la multiplicación\((Y \times R) \times L\)?
d. Ahora, vamos a hacer\(Y \times (R \times L)\). Comience por formar el tren\(R \times L\).
e. A continuación, formar el tren\(Y \times (R \times L)\). Poner la primera parte, Y, en la posición horizontal. La segunda parte\(R \times L\), formada en la parte d, debe ir en posición vertical como un tren largo, por debajo y perpendicular al tren Y. No separar las franjas de color verde claro en\(R \times L\) línea como un tren vertical largo (compuesto por más de una tira C verde claro) debajo de la tira en C amarilla. A la derecha, dibuje una imagen de cómo se ve esto hasta ahora.
f. hacer la multiplicación rellenando el resto de las tiras en C de color verde claro para formar el rectángulo, y luego haciendo un tren fuera del rectángulo de tiras en C de color verde claro. ¿Cuántas tiras en C de color verde claro hay en el tren formado por la multiplicación\(Y \times (R \times L)\)?
g. Compara la longitud del tren\((Y \times R) \times L\), de la parte c con la longitud del tren\(Y \times (R \times L)\), de la parte f. ¿Qué notas?
h. A partir de su observación, escriba una ecuación usando las tiras en C:
i. Traducir la ecuación de la parte h a una con números:
j. Escribe el lado izquierdo de la ecuación que escribiste en la parte i (que tiene números, no tiras C), y simplifica siguiendo el orden de las operaciones haz primero lo que está entre paréntesis. Entonces, haz lo mismo para el lado derecho de la ecuación.
Lado izquierdo:
Lado derecho:
k. ¿Son iguales las dos expresiones que simplificaste en la parte (j)? Si es así, has verificado que la ecuación de la parte (i) es verdadera.
Los ejercicios 11 y 12 ilustran la propiedad asociativa de la multiplicación para los trenes.
La propiedad asociativa de multiplicación para trenes establece que si r, s y t son tres trenes cualesquiera, entonces\((r \times s) \times t = r \times (s \times t\)).
Antes de pasar a más propiedades, practicaremos verificar que la propiedad asociativa de la multiplicación sea cierta para algunos números en base diez más adelante, lo haremos en otras bases, también. La propiedad asociativa requiere tres números (no tienen que ser tres números diferentes) y hay diferentes expresiones a cada lado de la ecuación. La diferencia entre los lados izquierdo y derecho es que los paréntesis están alrededor de un par diferente de números. Recuerde que la propiedad asociativa significa que hay un cambio de paréntesis, mientras que la propiedad conmutativa significa que ha habido un cambio de orden. Para verificar, es necesario utilizar el orden de las operaciones al simplificar cada lado. Si cada expresión se simplifica a lo mismo, la ecuación es verdadera. En el orden de las operaciones, siempre simplificas primero lo que está entre paréntesis. A continuación se presentan algunos ejemplos de cómo verificar la propiedad asociativa de la multiplicación, dado un conjunto de tres números.
La propiedad asociativa de multiplicación para números enteros establece que si a, b y c son tres números cualesquiera, entonces\(( a \times b ) \times c = a \times ( b \times c )\).
Verifica que la propiedad asociativa de multiplicación sea verdadera usando los tres números {4, 5, 7} en tu ejemplo.
Nota: Dado que los estados de propiedad asociativa\((a \times b) \times c = a \times (b \times c)\), uno de los números dados se pone en para a, el otro para b y el otro para c. La elección es suya. Por ejemplo, podemos mostrar que cualquiera de las siguientes seis ecuaciones son verdaderas:
| a.\((4 \times 5) \times 7 = 4 \times (5 \times 7)\) o d.\((4 \times 7) \times 5 = 4 \times (7 \times 5)\) |
| b.\((5 \times 4) \times 7 = 5 \times (4 \times 7)\) o e.\((7 \times 4) \times 5 = 7 \times (4 \times 5)\) |
| c.\((7 \times 5) \times 4 = 7 \times (5 \times 4)\) o f\((5 \times 7) \times 4 = 5 \times (7 \times 4)\). |
Si esto fuera una pregunta en una prueba, sólo habría que verificar una de las seis ecuaciones que se muestran siempre hay seis posibilidades que uno podría elegir, dependiendo de los números que ponga para a, b o c. Te mostraré cómo hacerlo si decidiste verificar la ecuación (e). También lo verificaré para otra ecuación (f). Entonces, para la práctica, se llega a verificar las otras cuatro ecuaciones.
Una solución al Ejemplo 1: Voy a mostrar:\((7 \times 4) \times 5 = 7 \times (4 \times 5)\)
Lado izquierdo:\((7 \times 4) \times 5 = 28 \times 5 = 140\) y lado derecho:\(7 \times (4 \times 5) = 7 \times 20 = 140\)
Como utilicé el orden de las operaciones para simplificar cada expresión, y ambas expresiones son iguales, la propiedad asociativa es verdadera usando los números 4, 5 y 7.
Aquí hay una manera diferente de verificarlo usando una ecuación diferente.
Otra solución al Ejemplo 1: Voy a mostrar:\((5 \times 7) \times 4 = 5 \times (7 \times 4)\)
Lado izquierdo:\((5 \times 7) \times 4 = 35 \times 4 = 140\) y lado derecho:\(5 \times (7 \times 4) = 5 \times 28 = 140\)
Como utilicé el orden de las operaciones para simplificar cada expresión, y ambas expresiones son iguales, la propiedad asociativa es verdadera usando los números 4, 5 y 7.
Verificar que la propiedad asociativa de multiplicación sea verdadera usando los números 4, 5 y 7, haciendo el orden de las operaciones en cada lado. Haz esto cuatro veces, usando las ecuaciones a, b, c y luego d, como se muestra en la página anterior.
| a. Verificar:\((4 \times 5) \times 7 = 4 \times (5 \times 7)\) |
| b. Verificar:\((5 \times 4) \times 7 = 5 \times (4 \times 7)\) |
| c. Verificar:\((7 \times 5) \times 4 = 7 \times (5 \times 4)\) |
| d. Verificar:\((4 \times 7) \times 5 = 4 \times (7 \times 5)\) |
Para verificar que la propiedad asociativa de la multiplicación es verdadera con el ejemplo, primero debes escribir una ecuación que debe ser verdadera usando tres números cualesquiera (o usando tres números particulares que se te hayan dado). Entonces, al hacer el orden de las operaciones en cada lado (cada expresión individual), se debe mostrar cada lado de la ecuación da el mismo resultado.
Verificar que la propiedad asociativa sea verdadera usando los números 10, 8 y 3.
a. voy a mostrar que esta ecuación es cierta:\((10 \times 8) \times 3 = 10 \times (8 \times 3)\)
Desde\((10 \times 8) \times 3 = 80 \times 3 = 240\) y\(10 \times (8 \times 3) = 10 \times 24 = 240\), entonces la ecuación\((10 \times 8) \times 3 = 10 \times (8 \times 3)\) es cierta.
Verifique que la propiedad asociativa sea verdadera usando los números dados.
a. {9, 7, 6}
b. cualquiera de los tres números de su elección.
Tiempo para trabajar en otra propiedad...
PASO 1: Formar el tren\(P \times (R + L)\). Para ello, la tira morada debe colocarse en posición horizontal, y el tren R + L debe colocarse en posición vertical debajo de la tira en c púrpura. Entonces, el rectángulo necesita rellenarse. Por último, hacer un tren largo fuera del rectángulo. Tenga en cuenta que este tren está conformado por 8 tiras en C (4 rojos y 4 verdes claros). Guarde este tren.
PASO 2: Formar dos trenes:\(P \times R\) y\(P \times L\). Después sumar los dos trenes juntos (en otras palabras,\(P \times R + P \times L)\) para formar un tren largo. Tenga en cuenta que este tren está conformado por 8 tiras en C (4 rojos y 4 verdes claros). Compara la longitud del tren formado en el Paso 1 con este tren. ¿Son de la misma longitud? ¿Están compuestos exactamente de las mismas tiras en C?
Eso acabamos de demostrar y verificar\(P \times (R + L) = P \times R + P \times L\).
a. formar el\(L \times (P + Y)\) tren formando primero el tren P + Y. Luego haga la multiplicación\(L \times (P + Y)\). ¿Exactamente qué tiras en C componen este tren?
b. Formar el tren\(L \times P\) y\(L \times Y\). Ahora agréguelos para formar un tren largo. ¿Exactamente qué tiras en C componen este tren?
c. Compara los trenes de las partes a y b, y escribe una ecuación (con tiras en C).
d. Traducir la ecuación de la parte c escribiendo una ecuación usando números.
e. Verifique la ecuación que escribió en la parte d simplificando primero el lado izquierdo de la ecuación usando el orden de las operaciones y luego simplificando también el lado derecho. Si la respuesta a cada expresión es la misma, has verificado la ecuación.
lado izquierdo:
lado derecho:
a. Formar el\(R \times (W + D)\) tren formando primero el tren W + D. Luego haga la multiplicación\(R \times (W + D)\). ¿Exactamente qué tiras en C componen este tren?
b. Formar el tren\(R \times W\) y\(R \times D\). Ahora agréguelos para formar un tren largo. ¿Exactamente qué tiras en C componen este tren?
c. Compara los trenes de las partes a y b, y escribe una ecuación (con tiras en C).
d. Traducir la ecuación de la parte c escribiendo una ecuación usando números.
e. Verifique la ecuación que escribió en la parte d simplificando primero el lado izquierdo de la ecuación usando el orden de las operaciones y luego simplificando también el lado derecho. Si la respuesta a cada expresión es la misma, has verificado la ecuación.
lado izquierdo:
lado derecho:
Los problemas anteriores ilustran la propiedad distributiva de la multiplicación sobre la suma para los trenes.
La propiedad distributiva de multiplicación sobre suma para trenes establece que si r, s y t son tres trenes cualquiera (cada tren puede estar compuesto por una o más tiras C), entonces\(r \times (s + t) = (r \times s) + (r \times t)\).
Ahora, es el momento de practicar verificar que la propiedad distributiva de la multiplicación sobre la suma es cierta para algunos números en base diez — más adelante, lo haremos en otras bases, también. La propiedad distributiva requiere tres números (no tienen que ser tres números diferentes) y hay dos lados de una ecuación para verificar. Observe la diferencia entre los lados izquierdo y derecho. Para verificar, es necesario utilizar el orden de las operaciones al simplificar cada lado. En el orden de las operaciones, siempre simplificas primero lo que está entre paréntesis. Si cada expresión se simplifica a lo mismo, la ecuación es verdadera. A continuación se presentan algunos ejemplos de cómo verificar la propiedad distributiva de la multiplicación, dado un conjunto de tres números.
La propiedad distributiva de multiplicación sobre suma para números enteros establece que si a, b y c son tres números cualesquiera, entonces\(a \times (b + c) = (a \times b) + (a \times c)\).
Verifica que la propiedad distributiva de la multiplicación sea verdadera usando los tres números {4, 5, 7} en tu ejemplo.
Nota: Dado que los estados de propiedad distributiva\(a \times (b + c) = (a \times b) + (a \times c)\), uno de los números dados se pone en para a, el otro para b y el otro para c. La elección es suya. Por ejemplo, podemos mostrar que cualquiera de las siguientes seis ecuaciones son verdaderas:
| a.\(4 \times (5 + 7) = (4 \times 5) + (4 \times 7)\) o d.\(5 \times (7 + 4) = (5 \times 7) + (5 \times 4)\) |
| b.\(4 \times (7 + 5) = (4 \times 7) + (4 \times 5)\) o e.\(7 \times (4 + 5) = (7 \times 4) + (7 \times 5)\) |
| c.\(5 \times (4 + 7) = (5 \times 4) + (5 \times 7)\) o f.\(7 \times (5 + 4) = (7 \times 5) + (7 \times 4)\) |
Si esto fuera una pregunta en una prueba, solo habría que verificar una de las seis ecuaciones mostradas. Siempre hay seis posibilidades que uno podría elegir, dependiendo de los números que pongas para a, b o c. Te mostraré cómo hacerlo si decidiste verificar la ecuación (c). También lo verificaré para otra ecuación (f). Entonces, para la práctica, se llega a verificar las otras cuatro ecuaciones.
Una solución al Ejemplo 1: Voy a mostrar:\(5 \times (4 + 7) = (5 \times 4) + (5 \times 7)\)
Lado izquierdo:\(5 \times (4 + 7) = 5 \times (11) = 55\) y lado derecho:\((5 \times 4) + (5 \times 7) = 20 + 35 = 55\)
Como utilicé el orden de las operaciones para simplificar cada expresión, y ambas expresiones son iguales, la propiedad distributiva es verdadera usando los números 4, 5 y 7.
Aquí hay una manera diferente de verificarlo usando una ecuación diferente.
Otra solución al Ejemplo 1: Voy a mostrar:\(7 \times (5 + 4) = (7 \times 5) + (7 \times 4)\)
Lado izquierdo:\(7 \times (5 + 4) = 7 \times 9 = 63\) y lado derecho:\((7 \times 5) + (7 \times 4) = 35 + 28 = 63\)
Como utilicé el orden de las operaciones para simplificar cada expresión, y ambas expresiones son iguales, la propiedad distributiva es verdadera usando los números 4, 5 y 7.
Verificar que la propiedad distributiva de multiplicación sea verdadera usando los números 4, 5 y 7, haciendo el orden de las operaciones en cada lado. Haga esto cuatro veces, utilizando las ecuaciones a, b, d y luego e, como se muestra en la página anterior.
| a. Verificar:\(4 \times (5 + 7) = (4 \times 5) + (4 \times 7)\) |
| b. Verificar:\(4 \times (7 + 5) = (4 \times 7) + (4 \times 5)\) |
| c. Verificar:\(5 \times (7 + 4) = (5 \times 7) + (5 \times 4)\) |
| d. Verificar:\(7 \times (4 + 5) = (7 \times 4) + (7 \times 5)\) |
Para verificar que la propiedad distributiva de la multiplicación es verdadera con el ejemplo, primero debes escribir una ecuación que debe ser verdadera usando tres números cualesquiera (o usando tres números particulares que se te hayan dado). Entonces, al hacer el orden de las operaciones en cada lado (cada expresión individual), se debe mostrar cada lado de la ecuación da el mismo resultado.
Verificar que la propiedad distributiva sea verdadera usando los números 10, 8 y 5.
a. voy a mostrar que esta ecuación es cierta:\(10 \times (8 + 5) = (10 \times 8) + (10 \times 5)\)
Solución
Desde\(10 \times (8 + 5) = 10 \times 13\) y\((10 \times 8) + (10 \times 5) = 80 + 50\), entonces la ecuación\(10 \times (8 + 5) = (10 \times 8) + (10 \times 5)\) es cierta.
Verificar que la propiedad distributiva de multiplicación sobre suma sea verdadera para los tres números especificados:
| a. {7, 8, 12} |
| b. {28, 65, 35} |
| c. cualquiera de los tres números de su elección. |
Utilice la definición de multiplicación para trenes para calcular lo siguiente. Después traduzca para hacer una ecuación usando números.
a.\(W \times R\) = _____ se traduce en _______________
b.\(W \times B\) = _____ se traduce a _______________
c.\(W \times D\) = _____ se traduce a _______________
d.\(W \times S\) = _____ se traduce a _______________
e.\(N \times W\) = _____ se traduce a _______________
f.\(H \times W\) = _____ se traduce a _______________
El ejercicio 19 ilustra que 1 es el elemento de identidad para la multiplicación. En otras palabras, para cualquier número m,\(\bf m \times 1 = m\) y\(\bf 1 \times m = m\).
El elemento de identidad para multiplicar si nos referimos a trenes es lo que rellenas el espacio en blanco para hacer verdadera la siguiente afirmación. Rellene los espacios en blanco para encontrar la identidad.
Para cualquier tren t,\(\bf t \times\) _____\(\bf = t\) y _____\(\bf \times t = t\).
La propiedad distributiva de la multiplicación sobre la suma se utiliza con bastante frecuencia para simplificar los problemas aritméticos. Considera los siguientes ejemplos:
Alguien que necesitaba multiplicarse\(57 \times 102\) podría resultarle más fácil pensar en el problema como\(57 \times (100 + 2) = (57 \times 100) + (57 \times 2) = 5700 + 114 = 5814\).
Alguien que necesitaba calcular\(47 \times 38 + 47 \times 62\) podría darse cuenta de que esto es realmente lo mismo que\(47 \times (38 + 62) = 47 \times 100 = 4700\).
Este siguiente ejemplo ilustra que la multiplicación también distribuye sobre la resta:
Alguien que necesitaba multiplicarse\(38 \times 99\) podría resultarle más fácil pensar en el problema como\(38 \times (100 - 1) = (38 \times 100) - (38 \times 1) = 3800 - 38 = 3762\).
Utilice la propiedad distributiva de multiplicación sobre suma (o resta) para reescribir los siguientes problemas. Entonces, simplifique. Para d, e y f, conforman tres de sus propios problemas donde sería más fácil usar primero la propiedad distributiva antes de simplificarla. Mostrar cómo usar la propiedad y simplificar.
| a.\(764 \times 999\) |
| b.\(324 \times 102\) |
| c.\(83 \times 74 + 83 \times 26\) |
| d. |
| e. |
| f. |
Hasta el momento, se ha trabajado con tres operaciones; suma, resta y multiplicación. Has aprendido muchas propiedades. Tómese un poco de tiempo para reflexionar y revisarlos escribiendo las propiedades o respondiendo las preguntas como se indica a continuación:
| a. Exponer la propiedad asociativa de la multiplicación y dar un ejemplo. |
| b. declarar los bienes conmutativos de adición y dar un ejemplo. |
| c. Exponer el elemento de identidad para la adición y lo que significa y dar un ejemplo. |
| d. Determinar la propiedad conmutativa de la multiplicación y dar un ejemplo. |
| e. Determinar la propiedad distributiva de multiplicación sobre suma y dar un ejemplo. |
| f. exponer el elemento de identidad para la multiplicación y dar un ejemplo. |
| g. Proporcionar un contraejemplo para demostrar que la resta no es conmutativa |
| h. Declarar la propiedad asociativa de adición. |
| i. Proporcionar un contraejemplo para demostrar que la resta no es asociativa. |
Hay otra manera de definir la multiplicación usando la Teoría de Conjuntos. Para ello, hay que recordar cómo tomar el producto cartesiano de dos juegos, A y B.
El producto cartesiano del conjunto A con el conjunto B, que se escribe\(A \times B\) y se lee como “A cruz B” es el conjunto de todos los pares ordenados posibles (a, b), donde\(a \times A\) y\(b \times B\).
Si estás encontrando el producto cartesiano, la respuesta es un conjunto que contiene pares ordenados.
Si A = {x, y, z} y B = {a, b}, encuentra\(A \times B\).
Solución
\(A \times B\)= {(x, a), (x, b), (y, a), (y, b), (z, a), (z, b)}
Si E = {1, 2} y F = {2, 3}, encuentra\(E \times F\).
Solución
\(E \times F\)= {(1, 2), (1, 3), (2, 2), (2, 3)}
Escribe el producto cartesiano. ¡Cada respuesta es un conjunto que contiene pares ordenados!
a. {3, 4}\(\times\) {2, 6} = _______
b. {6, 7, 8, 9}\(\times\) {5} = ________
c. {r, s, t}\(\times\) {} = _________
d. {a}\(\times\) {a} = _________
e. {x, y}\(\times\) {x, y} = ________
f. {1, 3, 5}\(\times\) {1, 3, 5} = ________
Definición de Teoría de Conjuntos para Multiplicar dos números enteros:
Para cualquiera de dos conjuntos A y B,\(\bf n(A) \cdot n(B) = n(A \times B)\).
Es decir, para multiplicar dos números, a y b, escribir un conjunto A que tenga un elementos en él y otro conjunto B que tenga b elementos en él. Para encontrar el producto, escriba el
producto cartesiano de A y B y cuente los elementos en el conjunto.
Nota: No hay restricciones sobre qué elementos eliges para los conjuntos A y B. Pueden ser disjuntos o pueden tener elementos en común. Depende de ti.
Utilice la definición de multiplicación de la teoría de conjuntos para mostrar que\(3 \cdot 2 = 6\)
Solución
Sea A = {v, w, x} y B = {1, 2}. Dado que n (A) = 3 y n (B) = 2, entonces
\ (\ begin {aligned} 3\ cdot 2 && = n (A)\ cdot n (B) &&\ text {sustituyendo n (A) por 3 y n (B) por 2}\\
&& = n (A\ times B) &&\ text {por la teoría de conjuntos definición de multiplicación}\\
&& = n (\ {(v,1), (v, 2), (w, 1), (w, 2), (x, 1), (x, 2)\}) & amp; &\ text {calculando} A\ times B\\
&& =6 &&\ text {contando los elementos en} A\ times B\ end {alineado}\)
Por lo tanto,\(3 \cdot 2 = 6\).
Utilice la definición de multiplicación de la teoría de conjuntos para mostrar que\(1 \cdot 3 = 3\)
Solución
Sea A = {v} y B = {1, 2, 3}. Dado que n (A) = 1 y n (B) = 3, entonces
\ (\ begin {aligned} 1\ cdot 3 && = n (A)\ cdot n (B) &&\ text {sustituyendo n (A) por 1 y n (B) por 3}\\
&& = n (A\ times B) &&\ text {por la teoría de conjuntos definición de multiplicación}\
&& = n (\ {(v, 1), (v, 2), (v, 3)\}) &&\ text {calculando} A\ veces B\\
&& = 3 &&\ text {contando los elementos en} A\ times B\ end {alineado}\)
Por lo tanto,\(1 \cdot 3 = 3\)
Utilice la definición de multiplicación de la teoría de conjuntos para mostrar que\(2 \cdot 0 = 0\)
Solución
Sea A = {v, w} y B = {}. Dado que n (A) = 2 y n (B) = 0, entonces
\ (\ begin {aligned} 2\ cdot 0 && = n (A)\ cdot n (B) &&\ text {sustituyendo n (A) por 2 y n (B) por 0}\\
&& = n (A\ times B) &&\ text {por la teoría de conjuntos definición de multiplicación}\\
&& = n (\ {\\}) &&\ text {calculando} A \ times B\\
&& = 0 &&\ text {contando los elementos en} A\ times B\ end {alineado}\)
Por lo tanto,\(2 \cdot 0 = 0\)
Utilice la definición de multiplicación de la teoría de conjuntos para mostrar que\(4 \cdot 3 = 12\)
Solución
Sea A = {e, f, g, h} y B = {g, h, i}. Dado que n (A) = 4 y n (B) = 3, entonces
\ (\ begin {aligned} 4\ cdot 3 && = n (A)\ cdot n (B) &&\ text {sustituyendo n (A) por 2 y n (B) por 0}\\
&& = n (A\ times B) &&\ text {por la teoría de conjuntos definición de multiplicación}\
&& = n (\ {(e , g), (e, h), (e, i), (f, g), (f, h), (f, i), (g, g), (g, h), (g, i), (h, g), (h, h), (h, i)\}) &&\ text {calculando} A\ veces B\\
&& = 12 &&\ texto {contando los elementos en} A\ veces B\ end {alineado}\)
Por lo tanto,\(4 \cdot 3 = 12\)
Utilice la definición de multiplicación de la teoría de conjuntos para verificar cada multiplicación. Mostrar y justificar cada paso. Solo se muestra la solución a 24a en las soluciones.
a.\(5 \cdot 2 = 10\)
b.\(3 \cdot 1 = 10\)
c.\(0 \cdot 2\)
Aquí hay un enfoque más geométrico para definir la multiplicación de dos números enteros.
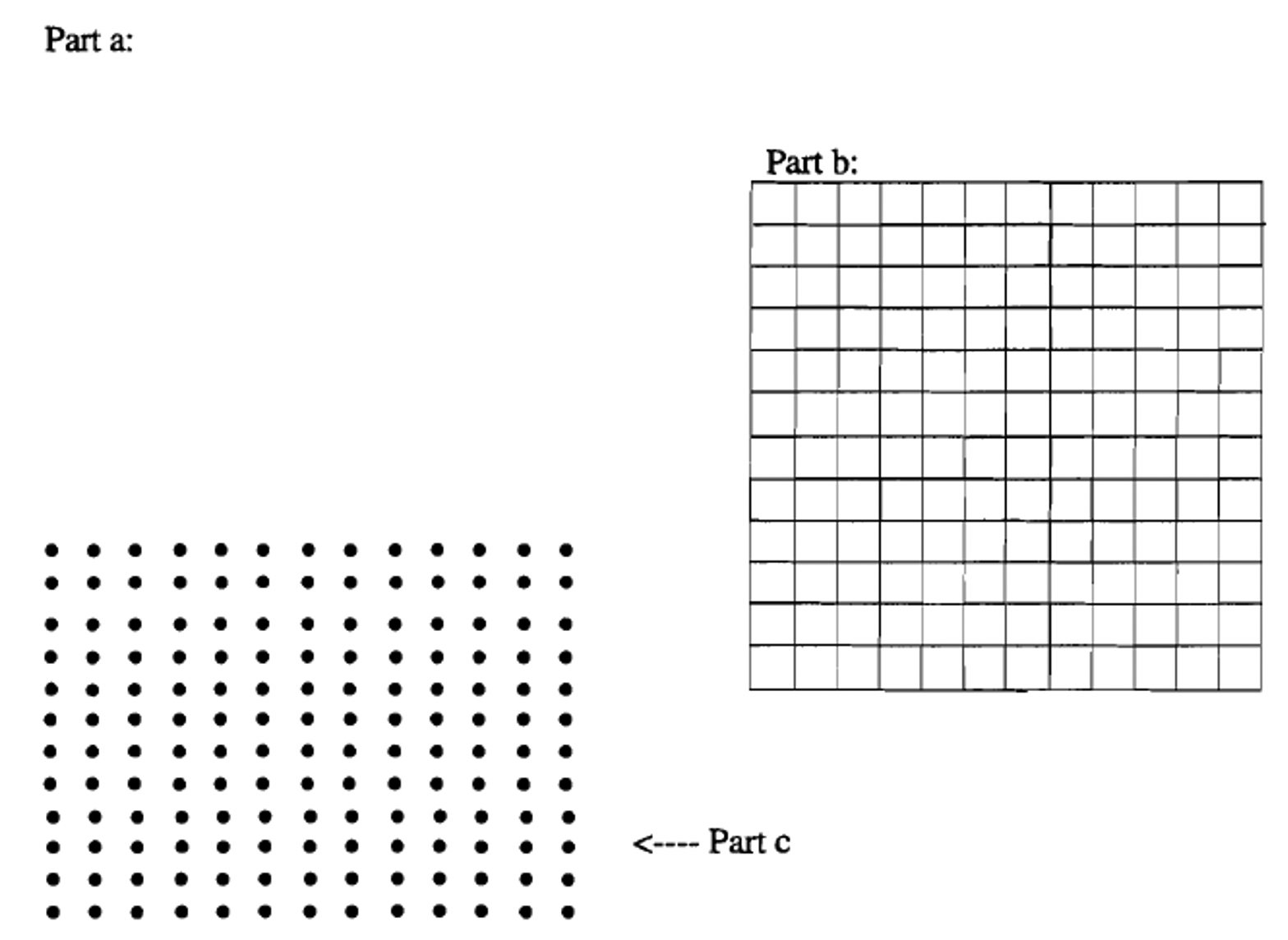
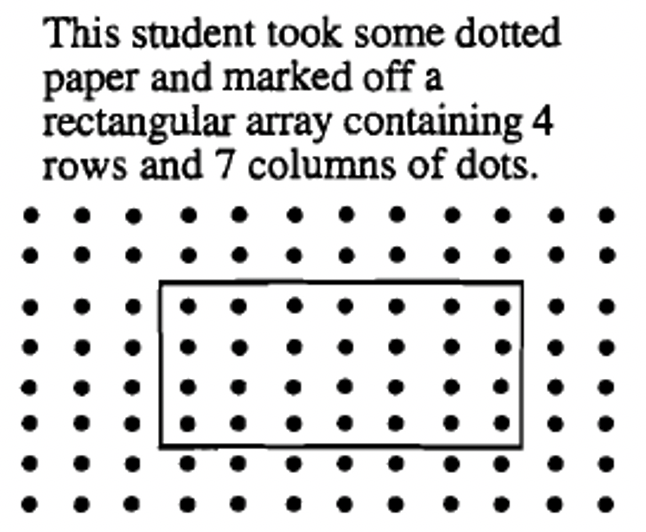
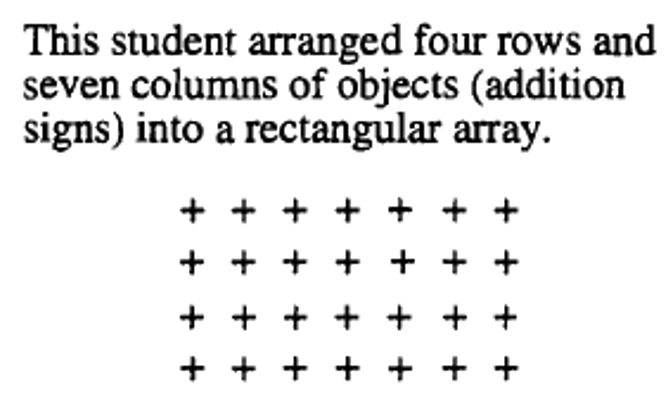
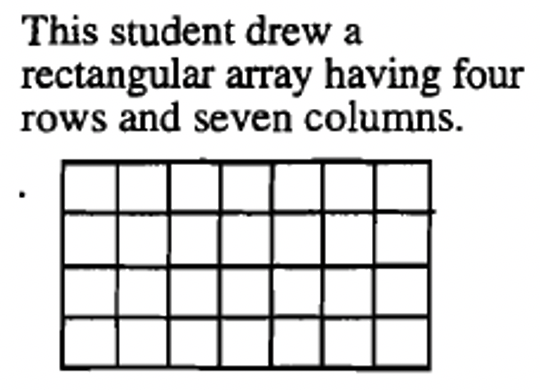
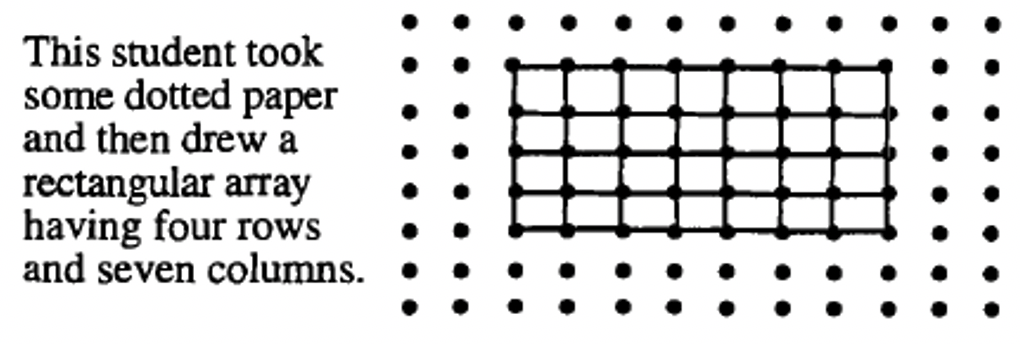
Para encontrar el producto de dos números enteros cualesquiera, m y n, haga una matriz rectangular de objetos que tengan m filas y n columnas. El producto de m y n, escrito\(m \times n\), equivale al número de objetos en la matriz.
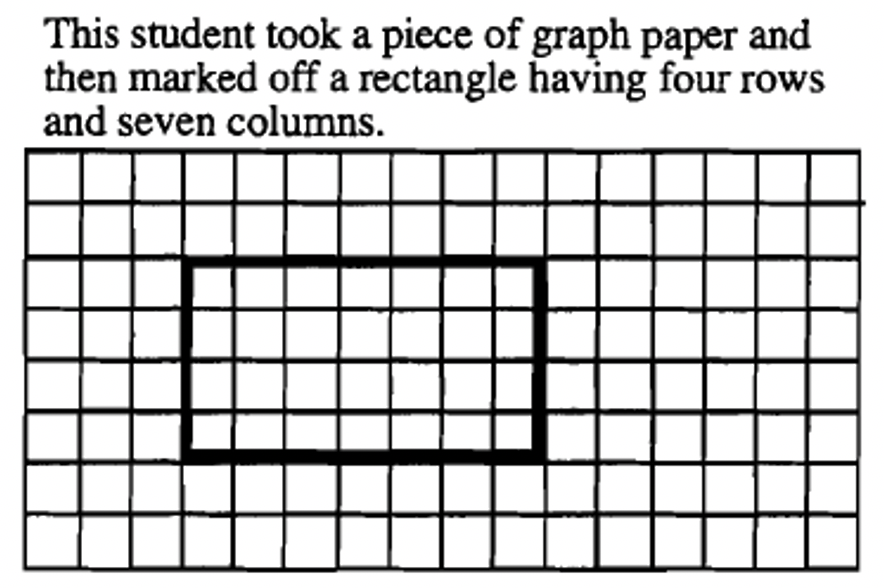
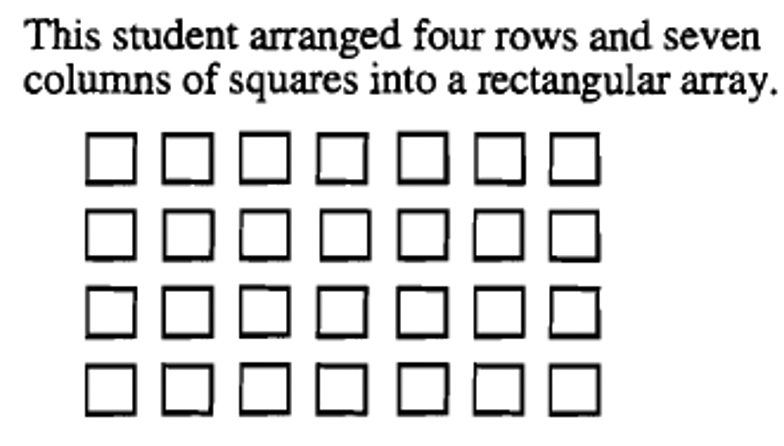
Lo bueno de usar este enfoque geométrico es que se puede usar cualquier objeto, y solo se necesita poder contar para obtener la respuesta. ¡No necesitas usar suma para multiplicar! Yo personalmente defiendo tener mucho papel cuadriculado alrededor para cualquiera que esté aprendiendo a multiplicarse. Para calcular\(4 \times 7\), usted o el alumno pueden marcar un rectángulo en el papel cuadriculado que tiene 4 filas y 7 columnas de cajas. El número de cajas en el rectángulo es la respuesta al problema. Esta es una herramienta útil para aprender primero un hecho particular de multiplicación, o para cualquiera (adultos, también) que olvidó un hecho y necesite resolverlo de nuevo. Los “objetos” utilizados en un papel cuadriculado son las cajas individuales en el papel cuadriculado.
Así es como seis estudiantes diferentes podrían mostrar geométricamente cómo multiplicarse\(4 \times 7\).
 |
 |
 |
 |
 |
 |
No tiene sentido hacer que alguien se estrese si se olvidó, no memorizó o no podía recordar la respuesta a\(4 \times 7\). El punto es SABER QUÉ SIGNIFICA LA MULTIPLICACIÓN para que puedas resolver de nuevo un problema si es necesario. Por supuesto, hay mérito en usar flashcards y eventualmente memorizar hechos básicos de multiplicación como tus tablas de multiplicación. Si no, lleva más tiempo hacer problemas, no puedes concentrarte en temas más avanzados y es posible que no confíes en tu propia mente. No deberías tener que pensar en la multiplicación cada vez que tienes que multiplicar dos números juntos, pero deberías poder pensarlo. Saber cómo obtener la respuesta es mejor que haber memorizado un montón de hechos si no sabes de dónde vinieron, qué significa realmente la multiplicación, o cómo resolverlo de nuevo en caso de que te olvides de la respuesta a algún hecho. Y, en lo que a mí respecta, ¡tampoco hay nada malo en usar los dedos! Que la gente haga lo que sea cómodo para ellos, si entienden y pueden obtener la respuesta correcta, ¡eso es genial!
Escribe el problema de multiplicación representado por cada representación geométrica:
|
a. ____ 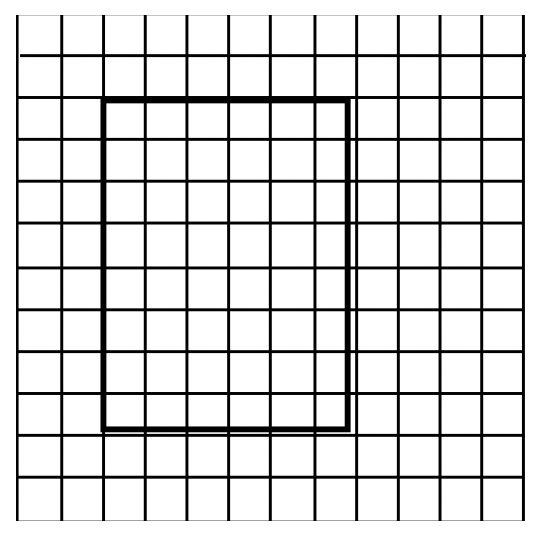 |
b. ____ 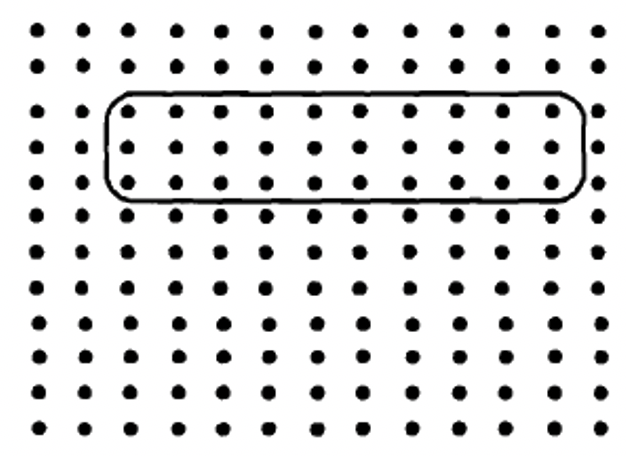 |
|
c. ____ \(%\begin{matrix} \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \\ \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge & \blacklozenge \end{matrix}\nonumber\)  |
d. ____  |
|
e. ____ 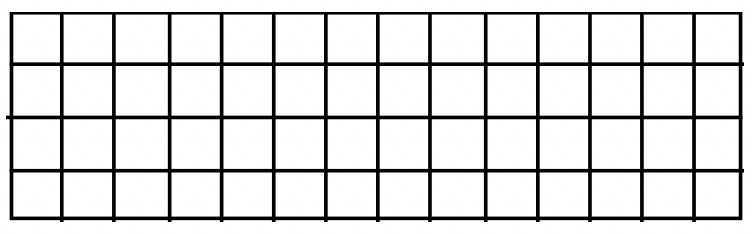 |
f. ____ 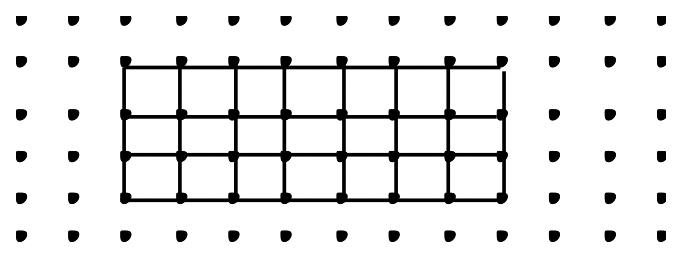 |
Mostrar dos representaciones geométricas diferentes para\(4 \times 3\)
Para cada multiplicación, haga lo siguiente para representar la multiplicación: Para la parte a, dibuje una matriz rectangular de objetos, para la parte b use el papel cuadriculado y para la parte c use el papel punteado. Hay dos formas en las que puedes elegir usar el papel punteado.
|
a.\(2 \times 6\)
|
|
|
b.\(5 \times 3\)
|
|
|
c.\(3 \times 7\)
|
a. Dibuja una matriz rectangular de cajas (un rectángulo) sobre el papel cuadriculado proporcionado para hacer la multiplicación\(4 \times 6\):

b. Gira tu página hacia los lados y mira el rectángulo. Dibuja cómo se ve la imagen:

c. ¿Qué problema de multiplicación se representa ahora? ________________
El ejercicio 28 debería convencerte de que la multiplicación es conmutativa. De hecho, la propiedad conmutativa de la multiplicación es más fácil de ver usando el enfoque geométrico. Una matriz rectangular de objetos con m filas y n columnas representa la multiplicación\(m \times n\). Una vez girado el rectángulo\(90^{\circ}\) (o mirado hacia los lados), ahora hay n filas y m columnas, lo que representa la multiplicación\(n \times m\). Pero claro, es realmente el mismo rectángulo de objetos, así que el número de objetos en\(m \times n\) es igual al número de objetos en\(n \times m\). Por lo tanto,\(m \times n = n \times m\). Bien, solo por diversión, una vez más:
La propiedad conmutativa de multiplicación para números enteros establece que si a y b son dos números cualesquiera, entonces\(a \times b = b \times a\).
¡Guau! ¿No es esto emocionante? Hay varias formas de pensar y definir la multiplicación, y podemos mostrar la propiedad conmutativa que aún conserva cada vez. ¿Se pone mejor que esto? Bueno,... SÍ... pero esa es otra historia.
Es un poco más complicado mostrar en una página bidimensional que tiene la propiedad asociativa de la multiplicación. Con tu trabajo con las tiras C, sabes que la multiplicación es asociativa. Aquí hay una manera de modelar geométricamente la multiplicación de tres números.
Para encontrar el producto de cualquiera de tres números enteros,\((a \times b) \times c\), primero hacer una matriz rectangular de cubos (dados, terrones de azúcar, etc.) teniendo a filas y b columnas. Después, rellena c capas del rectángulo inferior para obtener una caja rectangular, donde la base de la caja tiene ancho a y largo b, y la altura de la caja es c.
Básicamente, es necesario hacer (o visualizar) una caja tridimensional para hacer multiplicación en tres números. Resulta que, no importa cómo la construyas, si al final, una dimensión es a, una es b y la otra es c, tienes la misma caja, y contiene el mismo número de cubos en ella. Por lo tanto, la multiplicación es asociativa. No vamos a estar pasando por los movimientos de mostrarlo en 3 dimensiones, pero los niños de primaria deberían tener el beneficio de trabajar a través de ella con cubos. Espero que lo modele de esta manera si se convierte en profesor de primaria.
Dado que la multiplicación es a la vez conmutativa y asociativa, cada vez que se multiplican más de dos números, no es necesario mostrar los paréntesis, y los números se pueden multiplicar juntos en cualquier orden.
Por ejemplo, observe cuán diferente podría calcularse\(4 \times 10 \times 3 \times 5\)
Estudiante 1: Esta persona simplemente va de izquierda a derecha. Primero,\(4 \times 10\) es 40, luego\(40 \times 3\) es 120, luego\(120 \times 5 = 600\).
Estudiante 2: Esta persona primero multiplica\(4 \times 5\) para obtener 20, luego multiplica\(10 \times 3\) para obtener 30, luego multiplica las dos respuestas juntas,\(20 \times 30\) para obtener 600.
Estudiante 3: Esta persona lo hace\(4 \times 5\) primero para obtener 20, luego multiplica por 3 para obtener 60, luego multiplica por 10 para obtener 600.
Estudiante 4: Esta persona multiplica\(3 \times 5\) primero para obtener 15, luego multiplica eso por 4 para obtener 60, y luego multiplica por 10 para obtener 600.
Y hay muchas más posibilidades. El punto es que tienes la opción de multiplicar en cualquier orden y cualquier combinación que desees. A continuación se muestra cómo esto es muy conveniente para ciertos cálculos:
\(5 \times 87 \times 2\): Bueno, es más fácil multiplicar el 5 y 2 primero para obtener 10 y luego multiplicar por 87 para obtener 870. De lo contrario, podrías hacerlo\(5 \times 87\), lo que no es tan fácil de hacer en tu cabeza.
\(8 \times 22 \times 5\): Bueno, yo haría 8 veces 5 primero para obtener 40 y luego multiplicar por 22 para obtener 880.
Conforman un problema de multiplicación, donde sería más fácil multiplicar haciendo algunos reordenamientos primero. Explica tus pasos y cómo obtener la respuesta.
Eso lo vamos a mostrar\(3 \times (4 + 2) = (3 \times 4) + (3 \times 2)\). Primero trabajemos en el lado derecho de la ecuación, que tiene dos partes.
a. Dibuja una matriz rectangular de puntos o estrellas para representar\(3 \times 4\).
b. Ahora, dibuje una matriz rectangular de puntos o estrellas para representar\(3 \times 2\).
c. Dado que el lado derecho de la ecuación dice unir las dos partes (suma), luego dibuje la matriz de la parte a abajo, y justo al lado de ella, dibuje la matriz de la parte b.
d. Ahora, hagamos el lado izquierdo de la ecuación,\(3 \times (4 + 2)\). Primero tenemos que computar entre paréntesis para obtener\(3 \times 6\). Entonces, haz una matriz rectangular de puntos o estrellas para representar\(3 \times 6\).
e. ¿El número de puntos o inicios en la parte c es igual al número de puntos o arranques en la parte d?
¿Qué propiedad acabas de ilustrar en el ejercicio 30?
Bueno, espero que te des cuenta que acabas de demostrar que la multiplicación distribuye sobre la suma. De hecho, también es cierto que la multiplicación distribuye sobre la resta. En otras palabras,
Para tres números enteros cualesquiera, a, b y c, donde b > c,\(a \times (b + c) = (a \times b) + (a \times c)\) y\(a \times (b – c) = (a \times b) – (a \times c)\).
Demuéstralo\(2 \times (3 + 4) = (2 \times 3) + (2 \times 4)\) usando un enfoque geométrico, como lo hiciste en el ejercicio 30. Explique los pasos.
a. Formar el\(P \times (Y – L)\) tren formando primero el tren Y — L. Averigua qué es la tira C Y — L. Entonces haz la multiplicación\(P \times (Y – L)\). ¿Exactamente cuántas tiras C blancas componen este tren?
b. Formar el tren\(P \times Y\) y\(P \times L\). Ahora resta el segundo tren del primer tren. ¿Exactamente cuántas tiras C blancas componen este tren?
c. Comparar las longitudes de los trenes de las partes a y b.
El ejercicio 33 lo demostró\(P \times (Y – L) = P \times Y – P \times L\). Esta es una ilustración de que la multiplicación distribuye sobre la resta.