4.3: Tareas

Última actualización
Guardar como PDF

Page ID: 113215

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Envíe la tarea por separado de este libro de trabajo y grapa todas las páginas juntas. (Un elemento básico para la presentación completa de toda la tarea de la unidad)
Inicie un nuevo módulo en la parte frontal de una nueva página y escriba el número de módulo en la parte superior central de la página.
Las respuestas sin apoyar el trabajo no recibirán ningún crédito.
Algunas soluciones se dan en el manual de soluciones.
Puedes trabajar con compañeros de clase pero hacer tu propio trabajo.

HW #1

Utilice la definición de adición repetida de multiplicación para calcular lo siguiente. Primero, escribe el significado de la multiplicación, y luego computa la respuesta.

a.\(8 \times 4\)

b.\(4 \times 11\)

HW #2

Utilice la definición de adición repetida de multiplicación para calcular lo siguiente. Asegúrese de escribir el significado de la multiplicación en el sistema dado mostrando todo el trabajo y los intercambios. No hagas el problema en base diez.

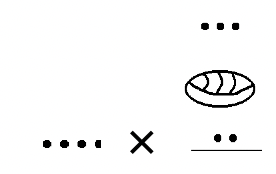
Screen Shot 2021-05-16 a las 10.12.33 AM.png

HW #3

Utilice la definición de multiplicación para trenes para calcular lo siguiente. Después traduzca para hacer una ecuación usando números.

a.\(P \times W = \) _____ se traduce a _______________

b.\(K \times W = \) _____ se traduce a _______________

HW #4

Escribir el producto cartesiano

a. {3, x}\(\times\) {0, 1, 6}

b. {a, b, 0}\(\times\) {1, 2}

HW #5

Usar la definición de multiplicación de la teoría de conjuntos para verificar\(3 \times 2 = 6\)

HW #6

Completa lo siguiente usando tus bloques base. Mostrar todo el trabajo.

a.\(F \times L\)

b.\(B \times L\)

c.\(F \times F\)

d.\(F \times B\)

e.\(B \times F\)

HW #7

Escribe la tabla de multiplicación base cuatro

HW #8

Calcula lo siguiente\(2506_{\text{seven}} \times 451_{\text{seven}}\) usando el método de celosía.

a.\(2506 \times 451\)

b.\(2506_{\text{seven}} \times 451_{\text{seven}}\)

HW #9

Calcular\(19 \times 24\) y\(24 \times 19\) usar el método Duplation. Mostrar todos los pasos.

HW #10

Para cada conjunto de tres números dados, ilustrar un ejemplo de la propiedad asociativa de la multiplicación, y luego ilustrar un ejemplo de la propiedad distributiva de la multiplicación sobre la suma. Siga los procedimientos descritos en este módulo

a.\(2_{\text{five}}, 3_{\text{five}}, 4_{\text{five}}\)

b.\(3_{\text{six}}, 4_{\text{six}}, 5_{\text{six}}\)