8.3: LCM y otros temas
- Page ID
- 113320
Necesitarás: Cuadrados de Números Primos (Tarjetas de Material 19A-19B)
Cuadrados de Números Compuestos (Tarjetas de Material 20A-20B)
Hay un número finito de factores para cualquier número dado. Por otro lado, hay un número infinito de múltiplos distintos de cero de un número. Por ejemplo la lista de múltiplos de 2 son todos los números pares. Es imposible enumerarlos todos, porque este es un conjunto infinito. Un múltiplo de un número c es nc donde n es un número entero. En otras palabras, para encontrar un múltiplo de c, multiplicar c por un número entero. Aunque 0 es un múltiplo de cada número, generalmente omitimos enumerarlo como múltiplo. Aquí se enumeran los múltiplos (distintos de cero) de 6:6, 12, 18, 24, 30, 36, 42,...
Para enumerar los múltiplos de un número, comienzas por el número en sí, luego el número por 2, luego el número por 3, etc. ya que la multiplicación se repite suma, podrías agregar repetidamente el número para obtener el siguiente múltiplo.
| a. Listar los primeros 10 múltiplos de 8: |
| b. Listar los primeros 10 múltiplos de 12: |
| c. de la lista que produjo en las partes a y b, enumere los múltiplos que 8 y 12 tienen en común: |
| d. De la parte c, ¿cuál es el múltiplo más pequeño que 8 y 12 tienen en común? |
| e. ¿Existe un mayor múltiplo común que 8 y 12 tienen en común? Es así, ¿qué es? Antes de responder, recuerda que en a y b, solo enumeraste los primeros 10 múltiplos de 8 y 12. |
Al igual que con el mayor factor común (GCF), mucha gente realmente no piensa en lo que significa MÚLTIPLE MENOS COMÚN. Cada número tiene un número infinito de múltiplos. Cada conjunto de números tiene un número infinito de múltiplos en común. El MÍLTIPLE MENOS COMÚN es el múltiplo más pequeño que
En el ejercicio 1, escribimos LCM (8, 12) = 24. El orden de los números entre paréntesis es irrelevante. Entonces, LCM (8, 12) = LCM (12, 8). NO es un par ordenado. Además, puedes encontrar el múltiplo menos común de un gran conjunto de números. Pronto descubrirás lo fácil que es encontrar el mínimo común múltiplo de varios números; p. ej., MCM (2, 3, 4, 5, 6, 7, 8, 9, 10). En este caso, enumerar varios múltiplos de cada uno de estos números hasta que encuentres el más pequeño que todos tienen en común no es la manera eficiente de encontrarlo, por lo que estarás explorando otra forma de encontrarlo usando la factorización prima.
| a. Listar los primeros 15 múltiplos de 4: |
| b. Listar los primeros 15 múltiplos de 6: |
| c. Enumere los primeros 15 múltiplos de 10: |
| d. de la lista que produjo en las partes a, b y c, enumere los múltiplos que los tres números (4, 6 y 10) tienen en común: |
| e. De la parte d, complete lo siguiente: LCM (4, 6, 10) = |
El problema de tratar de encontrar el múltiplo menos común de esta manera es que es posible que tengas que escribir una larga lista de múltiplos de cada número hasta que finalmente encuentres un múltiplo que todos tienen en común. Por ejemplo, si te pidieran encontrar el LCM (59,61), no encontrarías un múltiplo que cada uno tiene en común hasta que escribas 61 múltiplos de 59 y 59 múltiplos de 61. Eso se debe a que estos son números primos, así que el múltiplo menos común es su producto:\(59 \cdots 61\). Este es el caso de cualquier número que sea relativamente primo también. (Recuerda que 4 y 15 son relativamente primos, aunque ninguno es primo.)
Si x e y no tienen factores en común, entonces GCF (x, y) = 1 y LCM (x, y) = xy.
También es cierto lo siguiente:
Si GCF (x, y) = 1, entonces x e y no tienen factores en común, y LCM (x, y) = xy.
Si LCM (x, y) = xy, entonces x e y no tienen factores en común, y GCF (x, y) = 1.
Una manera más eficiente de encontrar el múltiplo menos común de un conjunto de números es encontrar la factorización prima de cada número, y luego CONSTRUIR el múltiplo menos común. Saca tus cuadrados de números primos para hacer los siguientes ejercicios.
A continuación se muestra la factorización primo de tres números, A, B y C.
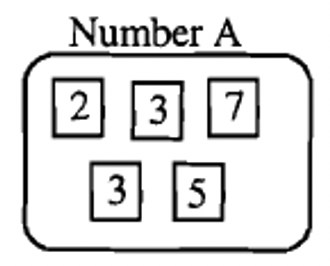 |
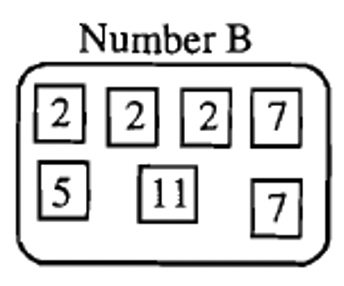 |
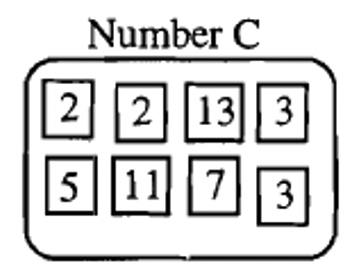 |
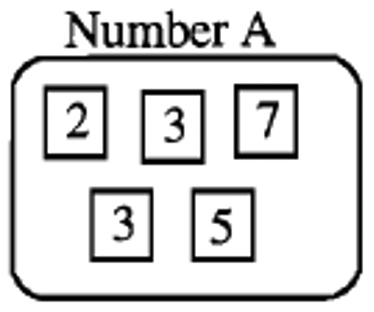
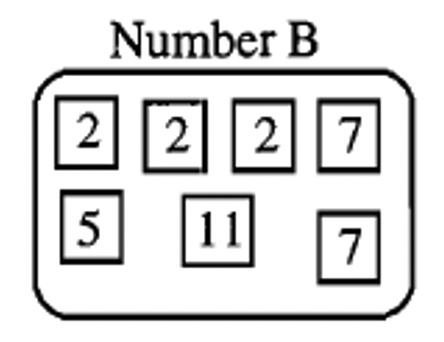
A continuación se muestra cómo escribir cada uno de estos números en forma de factorización prima:
| \(A = 2 \cdots 3^{2} \cdots 5 \cdots 7\) | \(B = 2^{3} \cdots 5 \cdots 7^{2} \cdots 11\) | \(C = 2^{2} \cdots 3^{2} \cdots 5 \cdots 7 \cdots 11 \cdots 13\) |
Una forma de hacer un múltiplo de A es simplemente agregar factores adicionales a factores de A. Nota: A en sí es un múltiplo de A, por lo que no es necesario agregar ningún factor adicional para obtener un múltiplo. Hay un número infinito de posibilidades para múltiplos de A. A continuación se muestran tres múltiplos de A:
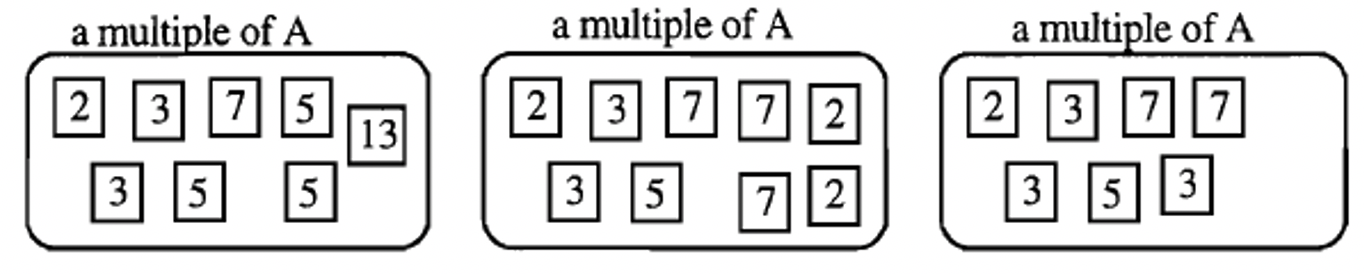
En forma de factorización prima, el primer múltiplo de A anterior está escrito:\(2 \cdots 3^{2} \cdots 5^{3} \cdots 7 \cdots 13\)
A continuación se muestra la factorización prima de un número, B
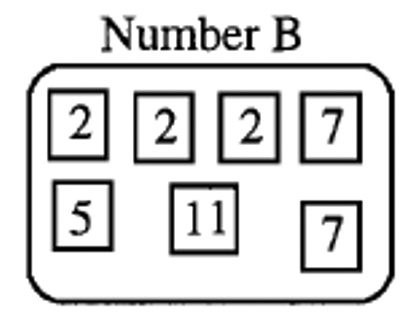
a. Forme el número B con sus cuadrados de números primos. Formar un múltiplo de B “arrojando” uno o más cuadrados de números primos como factores para la factorización prima original de B que se muestra arriba. Muestra una imagen del múltiplo de B que formaste.
Escribe la factorización principal de este múltiplo: _____
b. Forme el número B con sus cuadrados de números primos. Formar un múltiplo de B, diferente del que formaste en A, “arrojando” uno o más cuadrados de números primos como factores para la factorización prima original de B que se muestra arriba. Muestra una imagen del múltiplo de B que formaste:
Escribe la factorización principal de este múltiplo de B: _____
c. Forma el número B con tus cuadrados de números primos. Formar otro múltiplo de B “arrojando” uno o más cuadrados de números primos como factores para la factorización prima original de B que se muestra arriba. Escribe la factorización principal de este múltiplo de B: _____
El número C se muestra a continuación hacia la mitad de la página. Úselo para hacer ejercicio 4.
| a. Forme el número C con sus cuadrados de números primos. Formar un múltiplo de C sumando uno o más cuadrados de números primos como factores. Escribe la factorización principal del múltiplo de C que formaste: |
| b. Forme el número C con sus cuadrados de números primos. Formar un múltiplo diferente de C agregando uno o más cuadrados de números primos como factores. Escribe la factorización principal del múltiplo de C que formaste: |
| c. Forma el número C con tus cuadrados de números primos. Formar otro múltiplo de C sumando uno o más cuadrados de números primos como factores. Escribe la factorización principal del múltiplo de C que formaste: |
NOTA: X es un múltiplo de M si M es un factor de X. Entonces, tienes un múltiplo de un número si los factores primos del número en sí son factores en el múltiplo. Es como si se pudiera “ver” el número en un múltiplo. Vamos a determinar si alguno de los números que se muestran a la derecha son múltiplos de A, B o C.
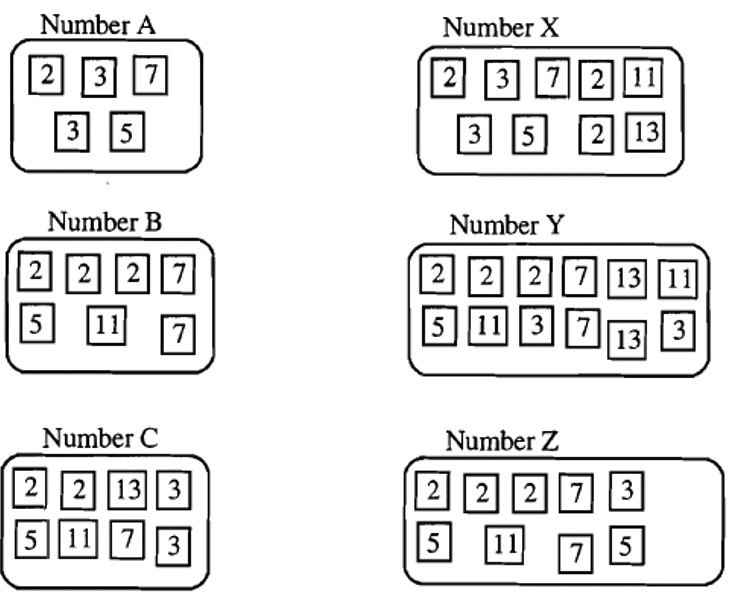
Para decidir si X, Y o Z es un múltiplo de A, vea si cada uno de X, Y o Z tiene los factores primos de A como subconjunto. Es decir, A tiene un factor de 2, dos factores de 3, un factor de 5 y un factor de 7. Cualquier número que contenga esos factores es un múltiplo de A. Un múltiplo de A puede tener más factores de A, pero no puede faltar ningún factor de A.
| a. Enumere cualquier número a la derecha (X, Y y/o Z) que sea un múltiplo de A: |
| b. Listar cualquier número a la derecha (X, Y y/o Z) que sea un múltiplo de B: |
| c. Enumere cualquier número a la derecha (X, Y y/o Z) que sea un múltiplo de C: |
Ninguno de los números X, Y o Z era múltiplo de los tres números, A, B y C. Los números A, B y C se muestran a continuación. Debajo de eso solo hay dos ejemplos de múltiplos que A, B y C tienen en común.
 |
 |
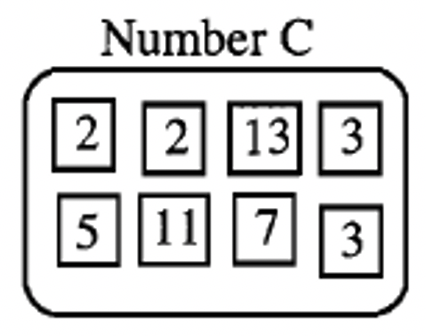 |
 |
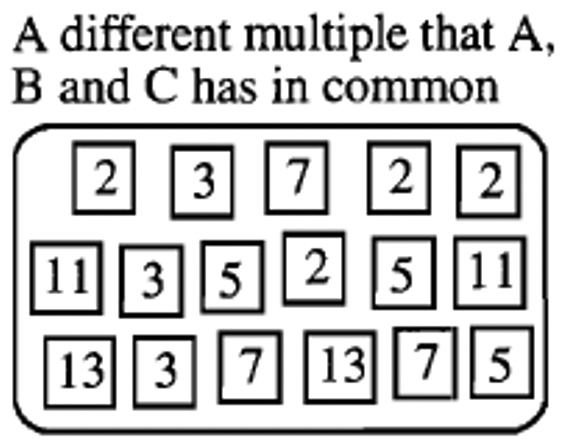 |
Usa cuadrados de números primos para formar otros tres múltiplos que A, B y C tienen en común. Escribe la factorización principal de cada uno de los múltiplos que has formado.
| a. _____ |
| b. _____ |
| c. _____ |
Ahora, vamos a usar la factorización prima para construir el MÚLTIPLE MENOS COMÚN de un conjunto de números. El múltiplo menos común es un múltiplo que los números tienen en común, pero que tiene el menor número de factores posibles. Los múltiplos formados anteriormente tienen 16 y 17 factores, respectivamente. Para construir un múltiplo menos común, solo agregamos en un factor si es necesario.
Digamos que queremos construir el mínimo común múltiplo de A, B y C. Para ser un múltiplo de A, necesitamos tener los factores de A. Entonces, comenzamos a construir el múltiplo poniendo en los factores de A:

Los factores de B también deben estar en el múltiplo. B tiene tres factores de 2, pero hasta el momento solo hay un factor de 2 en el múltiplo. Entonces, el múltiplo común necesitará dos factores más de 2. B tiene dos factores de 7, pero hasta el momento sólo hay un factor de 7 en el múltiplo. Entonces, el múltiplo común necesitará un factor más de 7. B tiene un factor de 5, que ya está ahí. B también tiene un factor de 11. Eso no está ahí, así que hay que ponerlo. Por lo tanto, dos factores de 2, un factor de 7 y un factor de 11 deben unirse con los otros factores en el múltiplo común. Una vez hecho esto, hemos construido el múltiplo menos común de A y B:

Las factorizaciones principales de A, B y C se muestran a continuación para su conveniencia.
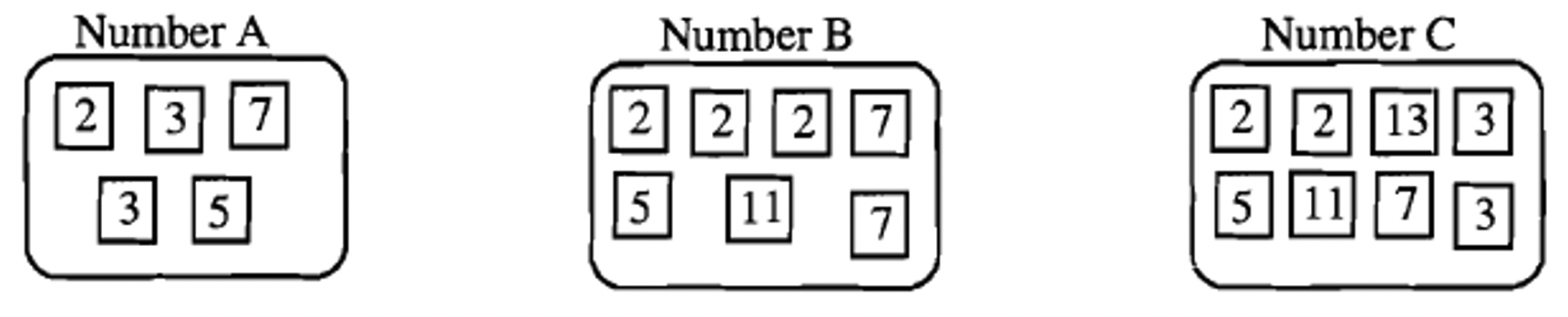
Hemos construido el múltiplo menos común de A y B. Para encontrar el múltiplo menos común de A, B y C, necesitamos asegurarnos de que los factores de C también estén en el múltiplo. C tiene dos factores de 2, que ya están en el múltiplo, dos factores de 3, que ya están en el múltiplo, un factor cada uno de 5, 7 y 11, cada uno de los cuales ya está en el múltiplo, y un factor de 13, que no está en el múltiplo. Entonces 13 es el único factor que hay que unir con los factores ya en el múltiplo que estamos construyendo.

Lo anterior es un múltiplo de A, B y C. Solo tenemos construimos un múltiplo, en realidad construimos el MÚLTIPLE MENOS COMÚN de A, B y C. Obsérvese que es un múltiplo de A, B y C; por lo tanto, es un múltiplo común. Es el múltiplo menos común porque si se eliminara alguno de los factores, no sería múltiplo de uno de los números. Por ejemplo, si se eliminara un factor de 2, no sería un múltiplo de A. Si se quitara un factor de 3, no sería múltiplo de A o C. Si se quitara un factor de 7, no sería múltiplo de B, etc. Si se eliminara un factor de 11, no sería múltiplo de B o C. Si se eliminara un factor de 13, no sería un múltiplo de C.
Escribimos: LCM (A, B, C) =\(2^{3} \cdots 3^{2} \cdots 5 \cdots 7^{2} \cdots 11 \cdots 13\)
Construye el múltiplo menos común de A y B usando cuadrados de números primos. Luego, escribe la factorización prima del múltiplo menos común de A y B. Let\(A = 2^{2} \cdots 3^{5} \cdots 5 \cdots 13\) y\(B = 2^{2} \cdots 3^{2} \cdots 7^{3} \cdots 11^{2} \cdots 13\)
LCM (A, B) = ____
Construye el múltiplo menos común de A, B y C usando cuadrados de números primos. Luego, escribe la factorización prima del múltiplo menos común de A y B.
Dejar A =\(2^{2} \cdots 11 \cdots 19\) y\(B = 2 \cdots 3^{2} \cdots 7 \cdots 11^{2}\) y\(C = 2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 13^{2} \cdots 19\)
LCM (A, B, C) = _____
Construye el múltiplo menos común de A, B y C usando cuadrados de números primos. Luego, escribe la factorización prima del múltiplo menos común de A y B.
Dejar\(A = 2 \cdots 5^{3} \cdots 11 \cdots 19\) y\(B = 2^{4} \cdots 3^{6} \cdots 5^{2} \cdots 23^{2}\) y\(C = 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 23\)
LCM (A, B, C) = _____
Mirar hacia atrás en la respuesta del ejercicio 9.
Dejar\(A = 2 \cdots 5^{3} \cdots 11 \cdots 19\) y\(B = 2 \cdots 3^{6} \cdots 5^{2} \cdots 23^{2}\) y\(C = 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 23\)
Respuesta: MCM (A, B, C) =\(2 \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 19 \cdots 23^{2}\)
Si los números se factorizan usando exponentes, entonces el múltiplo menos común contiene cada uno de los factores primos mostrados en cualquiera de los números. El exponente en cada uno de los números primos es el exponente más alto que se encuentra en ese factor de número primo en la factorización de los números primos.
Por ejemplo, los números primos en la factorización primo de A, B y C son 2, 3, 5, 7, 11, 19 y 23. Así que empieza por escribir el producto de estos números primos:\(2 \cdots 3 \cdots 5 \cdots 7 \cdots 11 \cdots 19 \cdots 23\)
2 es un factor en A y B. La potencia más alta de 2 que se encuentra en cualquiera de las dos factorización prima de A y B es 1. 3 es un factor que se encuentra en B, como\(3^{6}\). Entonces, la potencia más alta de 3 es 6. 5 es un factor de los tres números. En A, el exponente en 5 es 3; en B, el exponente en 5 es 2; en C, el exponente en 5 es 4. Entonces, el poder más alto de 5 es 4. Del mismo modo, haga lo mismo para todos los demás factores primos. Escribe el exponente más alto sobre el factor.
Por lo tanto, LCM (A, B, C) =\(2 \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 19 \cdots 23^{2}\)
Encuentra el mayor factor común y el mínimo común múltiplo para cada conjunto de números, escritos en factorización prima. Supongamos que a, b, c, d y e son números primos diferentes.
a. Dejar\(A = 2^{2} \cdots 3^{5} \cdots 5 \cdots 13\) y\(B = 2^{2} \cdots 3^{2} \cdots 7^{3} \cdots 11^{2} \cdots 13\)
| GCF (A, B) = ____________________________________________________ |
| LCM (A, B) = ____________________________________________________ |
b. Dejar\(A = 2^{2} \cdots 11 \cdots 19\) y\(B = 2 \cdots 3^{2} \cdots 7 \cdots 11^{2}\) y\(C = 2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 13^{2} \cdots 19\)
| GCF (A, B, C) = __________________________________________________ |
| LCM (A, B, C) = __________________________________________________ |
c. Dejar\(X = a^{5} \cdots b^{4} \cdots c^{5} \cdots d\) y\(Y = b^{2} \cdots c^{3} \cdots d^{2} \cdots e^{2}\) y\(Z = a^{2} \cdots c^{4} \cdots d^{3} \cdots e^{2}\)
| GCF (X, Y, Z) = __________________________________________________ |
| LCM (X, Y, Z) = __________________________________________________ |
d. Dejar\(X = a^{6} \cdots b^{3} \cdots c \cdots d\) y\(Y = b^{4} \cdots c^{4} \cdots d^{3} \cdots e^{7}\) y\(Z = a^{2} \cdots c^{4} \cdots d^{2} \cdots e^{3}\)
| GCF (X, Y, Z) = __________________________________________________ |
| LCM (X, Y, Z) = __________________________________________________ |
Hasta el momento, se ha dado la factorización de números primos, y todo lo que tenía que hacer era construir la factorización prima del múltiplo menos común. Ahora, tu trabajo será primero los números de factor primo; luego puedes construir el múltiplo menos común a partir de las factorizaciones principales. Al final, el múltiplo menos común es un número. Multiplique los factores en el múltiplo menos común para encontrar el número único que es el múltiplo menos común.
Encuentra el múltiplo menos común de 15, 18 y 20
Solución
Factor primo cada uno de estos números. \(15 = 3 \cdots 5, 18 = 2 \cdots 3 \cdots 3\), y\(20 = 2 \cdots 2 \cdots 5\)
Construye el múltiplo menos común “lanzando” primero los factores primos que componen la factorización principal de 15; luego “agrega” cualquier factor primo necesario para 18; a continuación, “agrega” cualquier factor primo necesario para 20. Obtenemos
LCM (15, 18, 20) =\(3 \cdots 5 \cdots 2 \cdots 3 \cdots 2 = 2^{2} \cdots 3^{2} \cdots 5\) = 180
Encuentra los múltiplos menos comunes. Muestra la factorización principal de cada número y cómo lo usas para construir el múltiplo menos común.
a. MCM (6, 8, 10) = ______
b. MCM (25, 35, 40) = ______
c. MCM (49, 91, 26) = ______
d. MCM (56, 24, 30) = ______
e. MCM (22, 34, 55) = _____
Observe lo fácil que es encontrar el múltiplo menos común de un conjunto de números más grande usando la factorización de primos. Encontraremos: LCM (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14)
No necesitamos anotar expresamente la factorización prime de los 12 números porque es bastante fácil hacerlo en nuestra cabeza. Por ejemplo, la factorización prima de 4 es\(2 \cdots 2\), la factorización prima de 10 es\(2 \cdots 5\), y la factorización prima de 13 es 13.
Construimos el LCM de 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 y 14 asegurándonos primero de que la factorización prime de 2 esté ahí.
Paso 1: Asegúrate de que la factorización principal 2 esté ahí. Hasta el momento, LCM: 2
Paso 2: Asegúrate de que la factorización principal 3 esté ahí. Tenemos que “lanzar” un 3 a la LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3\)
Paso 3: Asegúrate de que la factorización principal 4 esté ahí. Tenemos que “lanzar” un 2 a la LCM. Hasta el momento, LCM:\(\bf2 \cdots 3 \cdots 2\)
Paso 4: Asegúrate de que la factorización principal 5 esté ahí. Tenemos que “meter” un 5 a la LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5\)
Paso 5: Asegúrate de que la factorización principal 6 esté ahí. No necesitamos “agregar” ningún factor (s) al LCM, así que no hay ningún cambio en el LCM. Hasta el momento, LCM:\(2 \cdots 3 \cdots 2 \cdots 5\).
Paso 6: Asegúrate de que la factorización prima 7 esté ahí. Tenemos que “lanzar” un 7 a la LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7\)
Paso 7: Asegúrate de que la factorización principal 8 esté ahí. Tenemos que “lanzar” un 2 a la LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2\)
Paso 8: Asegúrate de que la factorización principal 9 esté ahí. Tenemos que “lanzar” un 3 a la LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3\)
Paso 9: Asegúrate de que la factorización prima 10 esté ahí. No necesitamos “agregar” ningún factor (s) al LCM, así que no hay ningún cambio en el LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3\)
Paso 10: Asegúrate de que la factorización prima 11 esté ahí. Tenemos que “meter” un 11 a la LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11\)
Paso 11: Asegúrate de que la factorización prima 12 esté ahí. No necesitamos “agregar” ningún factor (s) al LCM, así que no hay ningún cambio en el LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11\)
Paso 12: Asegúrate de que la factorización principal 13 esté ahí. Tenemos que “meter” un 13 a la LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11 \cdots 13\)
Paso 13: Asegúrate de que la factorización prima 14 esté ahí. No necesitamos “agregar” ningún factor (s) al LCM, así que no hay ningún cambio en el LCM. Hasta el momento, LCM:\(\bf 2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11 \cdots 13\)
¡Eso es! ¡Ahora has construido el mínimo múltiplo común de los 12 números! Puede verificar para asegurarse de que la factorización prima de cada uno de los 12 números esté de hecho en la factorización de primos del múltiplo menos común que construyó. Además, si se eliminara alguno de los factores primos, no sería múltiplo de todos los 12 números. Por lo tanto, la factorización prima del LCM es como se muestra a continuación:
LCM (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) =\(2 \cdots 3 \cdots 2 \cdots 5 \cdots 7 \cdots 2 \cdots 3 \cdots 11 \cdots 13\).
Si estos factores se multiplican juntos, LCM (2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14) = 360, 360.
La factorización prima de la LCM puede haber sido escrita con los factores en orden ascendente usando exponentes:\(2^{3} \cdots 3^{2} \cdots 5 \cdots 7 \cdots 11 \cdots 13\)
Utilice la factorización principal para construir el múltiplo menos común. Mostrar la factorización prima a medida que se construye el número. Después, multiplique los factores para encontrar la respuesta.
a. MCM (3, 4, 6, 7, 9, 10, 12, 14, 15, 18, 20) = _______ = _______
b. MCM (2, 3, 9, 11, 14, 15, 16, 17, 18, 22) = _______ = ________
c. MCM (5, 6, 7, 8, 12, 14, 15, 17, 18, 25) = _______ = _______
d. MCM (15, 18, 20, 25, 30, 35, 42, 45) = _______ = _______
Digamos que sabes que el mayor factor común de 165 y algún otro número fue 3, y el múltiplo menos común de los mismos dos números fue 15.015. ¿Cómo averiguarías cuál era el otro número?
Primero, es una buena idea anotar lo que sabes. Que N sea el otro número.
Entonces, GCF (165, N) = 3 y LCM (165, N) = 15,015.
Dado que 3 es un factor, y de hecho el mayor factor común, tanto de 165 como de N, entonces cada número se puede escribir como 3 veces algo, y el otro factor que obtenga para 165 debe ser relativamente primo al otro factor que obtenga para N, ya que 3 es el mayor factor común de 165 y N.
Entonces, vamos a reescribir, LCM (165, N) = 15,015 así: LCM (\(3 \times 55\),\(3 \times\) _____) = 15,015
Es decir, sé que N = 3\(\times\) _____, pero tengo que averiguar qué va en el espacio en blanco para averiguar qué es N. Si quieres introducir otra variable, como M, en lugar de escribir un espacio en blanco, eso funciona igual de bien. Depende de ti.
Para encontrar el LCM de\(3 \times 55\) y 3\(\times\) ______, donde el 55 y el número en el blanco no tienen factores comunes, multiplicarías\(3 \times 55 \times\) _______. Pero sabemos que el producto debe ser 15.015. Entonces, el número que debe ir en el espacio en blanco debe ser 91, ya que\(3 \times 55 \times 91 = 15,015\). Entonces, ahora podemos averiguar qué es N:\(N = 3 \times 91 = 273\).
Veamos si esto tiene sentido reescribiendo primero 165 y 273 ya sea en forma factorizada prima o como el GCF (165, 273) veces algo; entonces averiguaremos el GCF y LCM a partir de la forma factorizada, y veremos si concuerda con nuestro problema original.
\(165 = 3 \times 55\)y 273 =\(3 \times 91\). Primero, ¡asegúrate de que 3 es realmente un factor de cada número!
Ahora, convencerse de que 3 realmente es el mayor factor común de 165 y 273 comprobando para ver que el otro factor de un número es relativamente primo (no hay factores en común) con el otro factor del otro número. Entonces, pregúntese si 55 y 91 tienen algún factor en común (además de 1) si no está seguro, entonces factor primo cada uno de estos números primero (\(55 = 5 \times 11\)y\(91 = 7 \times 13\)); tenga en cuenta que no tienen factores en común.
Dado que 3 es el mayor factor común, entonces el múltiplo menos común se obtiene multiplicando\(3 \times 55 \times 91\), que es 15,015 que es lo que debería ser de acuerdo a la información original dada. Por lo tanto, 273 era realmente el número que buscábamos.
N = 273
Hay otra manera de hacer el problema anterior usando la siguiente propiedad:
Para dos números cualesquiera, m y n, siempre es cierto lo siguiente:
\(m \times n = GCF(m, n) \times LCM (m, n)\)
Esta ecuación no es cierta para más de dos números\(r \times s \times t \neq GCF(r, s, t) \times LCM(r, s, t)\)
Verificar la propiedad anterior para los números 15 y 18.
Dado que GCF (15, 18) = 3 y LCM (15, 18) = 90, queremos verificar que el producto de los dos números, 15 y 18, es igual al producto del GCF y LCM de los dos números.
\(15 \cdots 18 = 270\); GCF (15, 18)\(\cdots\) MCM (15, 18) =\(3 \cdots 90 = 270\)
Por lo tanto,\(15 \cdots 18 =\) GCF (15, 18)\(\cdots\) LCM (15, 18)
Demostrar que la propiedad anterior no funciona para tres números.
Contraejemplo: Usa los números 4, 6 y 8. GCF (4, 6, 8) = 2 y LCM (4, 6, 8) = 24
\(4 \cdots 6 \cdots 8 = 192\); GCF (4, 6, 8)\(\cdots\) MCM (4, 6, 8) =\(2 \cdots 24 = 48\)
Claramente,\(4 \cdots 6 \cdots 8 \neq\) GCF (4, 6, 8)\(\cdots\) LCM (4, 6, 8)
Encuentra N si GCF (165, N) = 3 y LCM (165, N) = 15,015
En este caso, los dos números son 165 y N, el GCF es 3 y el LCM es 15.015. Enchufe estos valores en la ecuación que se muestra arriba en negrita.
\(165 N = 3 \times 15,015\). Divide ambos lados por 165 para encontrar N: N =\(\frac{3 \times 15015}{165} = \) 273
La propiedad también se puede utilizar para encontrar el LCM de dos números si conoce el GCF. Por ejemplo, si te pidieron encontrar el GCF y LCM de 24 y 30. Puede encontrar fácilmente el GCF, que es 6. Para encontrar el MCM, multiplique los dos números juntos, y divídalo por el GCF. (Esto debería tener sentido para ti intuitivamente si lo piensas: No enumerarías el GCF dos veces mientras construyes el LCM. Además, el GCF cancelará en cualquiera de los dos números ya que es un factor de cada uno.) Entonces, el LCM (24, 30) =\((24 \cdot 30) \div 6 = 120\).
Si GCF (1176, 288) = 24, encuentre el MCM (1176, 288)
Encuentra X si GCF (2940, X) = 105 y LCM (2940, X) = 79,380
Si el mayor factor común de 3,211 y otro número es 247 y el mínimo común múltiplo de los mismos dos números es 48,165, entonces ¿cuál es el otro número?
Si no se le da al menos uno de los números, podría haber más de una solución posible. Averigua las posibilidades para a y b si todo lo que sabes es GCF (a, b) = 2 y LCM (a, b) = 20
Los siguientes problemas son una revisión de GCF y LCM. Ahora tiene varios métodos que puede utilizar para encontrar el GCF y LCM.
17-20 Encuentra el mayor factor común de cada uno de los siguientes pares de números usando la factorización de primos, el Método Chino Antiguo o el Algoritmo Euclidiana. Después, encuentra el LCM de cada par. Mostrar todo el trabajo.
| a. GCF (693, 546) = _______ |
| b. MCM (693, 546) = _______ |
| a. GCF (2117, 2555) = _______ |
| b. MCM (2117, 2555) = |
| a. GCF (1369, 10693) = ______ |
| b. MCM (1369, 10693) = |
| a. GCF (24300, 14406) = _______ |
| b. MCM (24300, 14406) = |
Informar un problema donde el GCF de 2 números diferentes de 3 dígitos es 32. Por ejemplo, GCF (x, y) = 32. Encuentra una x e y que funcione.
Informar un problema donde el GCF de dos números diferentes de 4 dígitos es 32. Es decir, encontrar 2 números, a y b, de tal manera que GCF (a, b) = 32.
Informar un problema donde el GCF de 2 números diferentes de 3 dígitos es 35. Por ejemplo, GCF (x, y) = 35. Encuentra una x e y que funcione.
Informar un problema donde el GCF de dos números diferentes de 4 dígitos es 28. Es decir, encontrar 2 números, a y b, de tal manera que GCF (a, b) = 28.
Todos los números pares son múltiplos de 2. Por lo tanto, cada número par puede escribirse como el producto de 2 y un entero. Simbólicamente, podemos escribir cada número par se puede escribir en la forma: 2k, donde k es un entero. Por ejemplo, 12 = 2 (6), 20 = 2 (10), 58 = 2 (29), etc.
Todos los números impares se pueden escribir como uno más que un número par. Dado que un número par se puede escribir como 2k, entonces simbólicamente, escribimos que cada número impar se puede escribir en la forma: 2k + 1, donde k es un entero. Por ejemplo, 15 = 2 (7) + 1, 41 = 2 (20) + 1, etc.
Cualquier entero que se pueda escribir en la forma 2k es par y cualquier entero que no se pueda escribir en la forma 2k no es par. Cualquier entero que se pueda escribir en la forma 2k + 1 es impar y cualquier entero que no se pueda escribir en la forma 2k + 1 no es impar.
Estaremos haciendo algunas pruebas sobre números pares e impares. La única forma de expresar un número par, en general, es por 2k. La variable puede ser de cualquier letra. Si quieres expresar más de un número par, debes usar una nueva variable como 2m o 2n. Lo mismo es cierto para los números impares.
Para los ejemplos y ejercicios que siguen, supongamos que todas las variables son números enteros.
EJEMPLOS: Indica cuál de los siguientes siempre representa un número par, cuál de los siguientes siempre representa un número impar, y cuáles son a veces pares y a veces impares.
6n + 14
Solución
6n + 14 = 2 (3n + 7), que está en forma de número par. Por lo tanto, 6n + 14 siempre representará un número par (ya que n es un entero).
4n + 23
Solución
4n + 22 + 1 = 2 (2n + 11) + 1, que es en forma de número impar. Por lo tanto, 6n + 14 siempre representará un número impar.
5n + 2
Solución
Es imposible escribir 5n + 2 en la forma 2k o 2k + 1. Por lo tanto, no se puede determinar. A veces es par y a veces extraño.
Nota: Puede verificar estas respuestas conectando un número par para n y luego un número impar para n, y ver si la conclusión tiene sentido. En el ejemplo 1, si n = 2, entonces 6n + 14 = 6 (2) + 14 = 28 (par). Si n = 3, entonces 6 (3) + 14 = 32 (par). Entonces, el resultado fue par cuando n fue reemplazado por un número par o impar. Haga la misma verificación por ejemplo 2 y 3 en el siguiente espacio:
Indica cuál de los siguientes siempre representa un número par, cuál de los siguientes siempre representa un número impar, y cuáles son a veces pares y a veces impares. Justifica tu respuesta.
a. 8n + 20
b. 10k + 9
c. 5x + 2
Demostrar formalmente que la suma de dos números impares es par.
Nota IMPORTANTE: No defina que los dos números impares sean el mismo número impar. Debes ser general, ¡y asumir que pueden ser dos números impares diferentes! Utilizar diferentes variables para ser las más generales.
Solución
Dejar 2n+1 = un número impar, y dejar 2m+1 = otro número impar.
La suma es: 2n+1 + 2m+1= 2n+2m+2 = 2 (n+m+1), que está en forma de número par. Por lo tanto, la suma de 2 números impares es par.
Demostrar formalmente que el producto de dos números impares es impar.
Solución
Dejar 2n+1 = un número impar, y dejar 2m+1 = otro número impar.
La suma es: (2n+1) (2m+1) = 4nm + 2m + 2n + 1 = 2 (2nm + n + m) +1, que está en forma de número impar. Por lo tanto, el producto de 2 números impares es impar.
Demostrar formalmente que la suma de dos números pares es par.
Demostrar formalmente que la suma de dos números impares es par.
Demostrar formalmente que la suma de un número par y un número impar es impar.
Demostrar formalmente que el producto de dos números pares es parejo.
Demostrar formalmente que el producto de dos números impares es impar.
Demostrar formalmente que el producto de un número par y un número impar es par.
Vamos a explorar una manera de encontrar la suma de varios números enteros consecutivos.
1 + 2 + 3 + 4 + 5 + 6
La suma de los primeros 100 números de conteo tardaría mucho en escribir y computar. Lo escribimos de la siguiente manera: 1 + 2 + 3\(\dots\) + 98 + 99 + 100
55 + 56 + 57 +\(\dots\) + 128 + 129 + 130
El primer ejemplo es bastante fácil de calcular. Pero a medida que se agregan más y más números, el cálculo se vuelve engorroso. Los dos primeros ejemplos comienzan con el número, 1. Nuestro primer objetivo será encontrar un patrón, y luego una fórmula para sumar cualquier conjunto de números de conteo consecutivos comenzando con 1.
Aunque sepamos la respuesta al ejemplo 1, la usaremos para encontrar un patrón para la suma de otras sumas. Dejar X = la suma que estamos buscando (1 + 2 + 3 + 4 + 5 + 6). Observe lo que sucede si X se anota dos veces, primero en orden ascendente, luego en orden descendente, y luego las dos filas se agregan agregando columnas alineadas:
| \(\begin{aligned} X = 1 + 2 + 3 + 4 + 5 + 6 \\ + \underline{X} = \underline{6} + \underline{5} + \underline{4} + \underline{3} + \underline{2} + \underline{1} \\ 2X = 7 + 7 + 7 + 7 + 7 + 7 \end{aligned}\) |
El lado izquierdo es igual a 2X, que es el doble de la suma real que queremos. ¿Cuántas columnas de números hay en el lado derecho del signo igual? _____ Nota: el número de columnas es el mismo que la cantidad de números en la suma real que estamos tratando de encontrar. ¿A qué suma cada columna del lado derecho del signo igual? _____ Dado que el lado derecho del signo igual es suma repetida, se puede obtener la respuesta usando la multiplicación. ¿Qué problema de multiplicación es este? _________ Dado que el lado izquierdo es igual al lado derecho (2X = 42), entonces X = 21. Incluso si no representaste la suma usando una variable, dividirías el lado derecho por 2 porque la suma es el doble de grande ya que los números en la suma se agregaron dos veces.
Usemos esta misma técnica para sumar los primeros 100 números de conteo consecutivos. Dejar N = la suma real. Rellenas la tercera fila agregando el lado izquierdo y luego agregando todas las columnas en el lado derecho.
| \(\begin{aligned} N = && 1 && + && 2 && + && 3 &&+ && \dots && + && 98 && + && 99 + && 100 \\ + \underline{N} = && \underline{100} && +&& \underline{99} && + && \underline{98} && + && \dots && + && \underline{3} && + && \underline{2} + && \underline{1} \end{aligned}\) |
¿Cuántas columnas (es la misma respuesta que la cantidad de números en la suma) hay a la derecha? ______ Dado que cada columna suma el mismo número, esto es adición repetida. Afirma el número que suma el lado derecho: ___________ Eso es el doble de grande que la suma real, entonces, ¿a qué es igual la suma (1 + 2\(\dots\) + 3 + 98 + 99 + 100)? ______
Ojalá, ¡obtuviste la respuesta de 5,050!
Utiliza la técnica anterior para encontrar la suma de los primeros 80 números de conteo. Mostrar trabajo
Tratemos de encontrar una fórmula para encontrar los primeros n números contando usando la misma técnica. Antes de escribir la suma, ¿cuál es el número de conteo que precede a n? _______ ¿Cuál es el número de conteo que precede a ese número? ______
Sea X = la suma de los primeros n números de conteo. A continuación, usaremos la misma techique para encontrar la suma. Rellene la suma en el lado izquierdo del lado igual y la suma de cada columna a la derecha.
|
|
¿A qué suma cada columna de la derecha? ________ Nuevamente, el lado derecho es una adición repetida nuevamente. Multiplique el número de columnas (que es igual a la cantidad de números en la suma de los primeros n números de conteo) por el número al que suma cada columna.
¿Qué es lo que iguala el lado derecho? _____________ Esto es dos veces más grande que la suma real que queremos.
¿Qué es igual la suma real de los primeros n números de conteo? _____________
Ojalá tengas esta respuesta:\(\frac{n(n+1)}{2}\)
Por supuesto, la respuesta depende de n. Vamos a usar esta fórmula para calcular la suma de los primeros seis números de conteo, que fue el primer ejemplo que hicimos. En este ejemplo, n = 6. Entonces, enchufando n = 6 en la fórmula, obtenemos\((6 \cdot 7)\)/2 = 21. ¡La misma respuesta!
Ejercicio 33
Usa la fórmula para encontrar la suma de los primeros 80 números de conteo.
Usa la fórmula para encontrar esta suma: 1 + 2 + 3\(\dots\) + 248 + 249 + 250.
¿Y si quisieras encontrar esta suma? 55 + 56 + 57 +\(\dots\) + 128 + 129 + 130
Si usaste la fórmula, entonces tendrías la suma de todos los números del 1 al 130 en lugar de solo los del 55 en adelante. Una estrategia es usar la fórmula y luego restar los números adicionales que agregaste. Por ejemplo, si agregas todos los números del 1 al 130, los números extra agregados que no forman parte de la suma son: 1 + 2 + 3\(\dots\) + 52 + 53 + 54. Pero esta suma es fácil de calcular ya que podemos usar la fórmula para obtener esta suma! Así que aquí está la estrategia:
55 + 56 + 57 +\(\dots\) + 128 + 129 + 130
= (la suma de los primeros 130 números de conteo) — (la suma de los primeros 54 números de conteo)
= (1 + 2 + 3 +\(\dots\) + 128 + 129 + 130) — (1 + 2 + 3\(\dots\) + 52 + 53 + 54)
\(\frac{130(131)}{2} - \frac{54(55)}{2}\)= 8,515 - 1,485 = 7,030
Encuentra la suma: 81 + 82 + 83 +\(\dots\) + 198 + 199 + 200
Solución
Restar la suma de los primeros 80 números de conteo de la suma de los primeros 200 números de conteo: 200 (201) /2 — 80 (81) /2 = 20,100 — 3,240 = 16,860.
Encuentra las siguientes sumas usando la estrategia que acabamos de mostrar. Mostrar trabajo.
a. 51 + 52 + 53 +\(\dots\) + 98 + 99 + 100
b. 146 + 147 + 148 +\(\dots\) + 561 + 562 + 563
c. 500 + 501 + 502\(\dots\) + 798 + 799 + 800
Hay una estrategia diferente que podemos usar para encontrar la suma de números enteros consecutivos que no comienzan con el número, 1. Veamos otra forma de calcular la suma de estos números enteros: 55 + 56 + 57\(\dots\) + 128 + 129 + 130. Comenzaremos usando el mismo tipo de estrategia que usamos al inicio de este tema. Primero, vamos X = la suma. Anote la suma dos veces, primero en orden ascendente, luego en orden descendente, y luego agregue las dos filas agregando las columnas individuales alineadas. Esto se muestra en la página siguiente.
| \(\begin{aligned} X = & 55 + & 56& + & 57 &+ & \dots &+& 128 &+& 129 &+ &130 \\ \underline{X} =& \underline{130} + &\underline{129}& +& \underline{128} &+ & \dots &+ & \underline{57} &+ & \underline{56}& + \underline{55} \\ 2X = &185 + & 185& +& 185 &+ &\dots &+& 185 &+ &185 &+ &185 \end{aligned}\) |
En este punto, podemos ver la similitud con cómo derivamos la suma de los primeros n números de conteo, pero aquí hay una gran diferencia. No está claro exactamente cuántas adiciones de 185 hay en el lado derecho del signo de iguales. La mayoría de la gente dirá que hay 130 — 55, o 75 de ellos, pero en realidad ese razonamiento (restar el primer número del último número) no es correcto. Por ejemplo, si estuvieras sumando los números del 1 al 130, la mayoría de la gente estará de acuerdo en que se están sumando 130 números, que NO es la misma respuesta que obtendrías si restaras el primer número del último número ya que 130 — 1 solo equivale a 129. Mira ejemplo más sencillo: 17 + 18 + 19 + 20. Está claro que hay 4 números en la suma, pero si hicieras la resta 20 — 17, obtendrías 3, que es la respuesta incorrecta. Una forma de averiguar cuántos números hay en la suma es decidir cuántos números faltan de la suma si comenzó con 1. Mira de nuevo la suma: 17 + 18 + 19 + 20 le faltan los primeros 16 números, así que en lugar de 20 números en la suma (que es cuántos habría si empezáramos en 1), hay 20 — 16 números en la suma. Bien, volvamos a averiguar cuántos números hay realmente en la suma anterior.
¿Cuántos números hay en la suma: 55 + 56 + 57\(\dots\) + 128 + 129 + 130? _______
Entonces, el lado derecho de la ecuación tiene 76 185 sumados, que es 76\(\cdots\) 185, lo que equivale a 14.060. Pero, esto es el doble de grande que la suma real, así que después de dividir por 2, obtenemos la suma real de 7.030. Esta es la misma respuesta que obtuvimos cuando hicimos este problema en la página anterior usando una estrategia diferente.
Encuentra las siguientes sumas usando la estrategia que acabamos de mostrar. Mostrar trabajo.
a. 51 + 52 + 53 +\(\dots\) + 98 + 99 + 100
b. 146 + 147 + 148 +\(\dots\) + 561 + 562 + 563
c. 500 + 501 + 502\(\dots\) + 798 + 799 + 800
d. Desafío: k + (k + 1) + (k + 2)\(\dots\) + (n - 2) + (n - 1) + n
Hasta el momento, has aprendido a encontrar fácilmente la suma de varios números enteros consecutivos. Vamos a dar un paso más allá. Y si la suma que quieres encontrar son números que no son consecutivos. Dependiendo de la secuencia de números, la suma puede o no ser fácil de encontrar. Vamos a ver sumas que tienen números consecutivos sumados disfrazados. Por ejemplo, mira la siguiente suma:
7 + 14 + 21 +\(\dots\) + 693 + 700
¿Qué notas sobre los números que se suman?
Ojalá te hayas dado cuenta de que todos los números eran múltiplos de siete, o tal vez notaste que agregas siete a cada número para obtener el siguiente número. Tome la suma y reescriba el problema factorizando un 7; solo complete los espacios en blanco a continuación:
7 + 14 + 21 +\(\dots\) + 693 + 700 = 7 (____ + ____ + ____ + + ____\(\dots\) + ____ + ____)
Ahora, deberías poder calcular la suma de los números entre paréntesis. Muestra tu trabajo para calcular la suma. Entonces contestan a, b y c.
a. ¿Cuál es la suma de los números entre paréntesis? __________
b. entonces, la suma 7 + 14 + 21 + 28 +\(\dots\) + 700 se convierte en 7 _________
c. Por lo tanto, 7 + 14 + 21 + 28 +\(\dots\) + 700 = _______________
Encuentra las siguientes sumas. Muestra tu trabajo.
a. 8 + 16 + 24 +\(\dots\) + 992 + 1000 = ____________
b. 11 + 22 + 33 +\(\dots\) + 935+ 946 = _____________
c. 20 + 40 + 60 + 80 +\(\dots\) + 2980 + 3000 = _____________
Bien, sólo un giro más... esto lo pone todo junto. Considera esta suma:
112 + 116 + 120 +\(\dots\) + 524 + 528
Esta vez, ¿qué nota de los números sumados?
Ojalá te hayas dado cuenta de que todos los números eran múltiplos de cuatro, o que agregaste cuatro a cada número para obtener el siguiente número. Tome la suma y reescriba el problema factorizando un 4; solo complete los espacios en blanco a continuación:
112 + 116 + 120 + 524\(\dots\) + 528 = 4 (____ + ____ + ____ + + _____\(\dots\) + _____ + _____)
Ahora, deberías poder calcular la suma de los números entre paréntesis. Tenga en cuenta que la suma no comienza con un 1. Muestra tu trabajo para calcular la suma. Entonces contestan a, b y c.
a. ¿Cuál es la suma de los números entre paréntesis? __________
b. entonces, la suma 112 + 116 + 120 + 524\(\dots\) + 528 pasa a ser 4 _________
c. Por lo tanto, 112 + 116 + 120 +\(\dots\) + 524 + 528 = _______________
Encuentra las siguientes sumas. Muestra tu trabajo.
a. 85 + 90 + 95 +\(\dots\) + 735 + 740 = ____________
b. 430 + 473 + 516 +\(\dots\) + 2838+ 2881 = _____________
Aquí hay algunos problemas para que descubras qué números están en la línea numérica. Para cada problema, averigua en qué lugar de la recta numérica (qué número) podría estar parado el hombre. Donde haya más de una posibilidad, solo enumere números entre 1 y 1000.
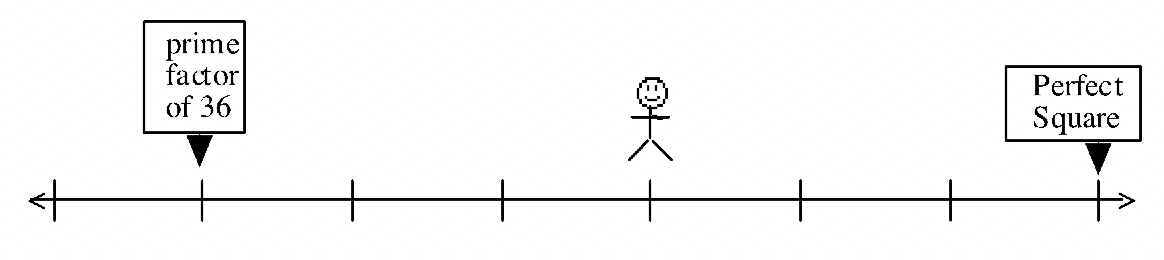

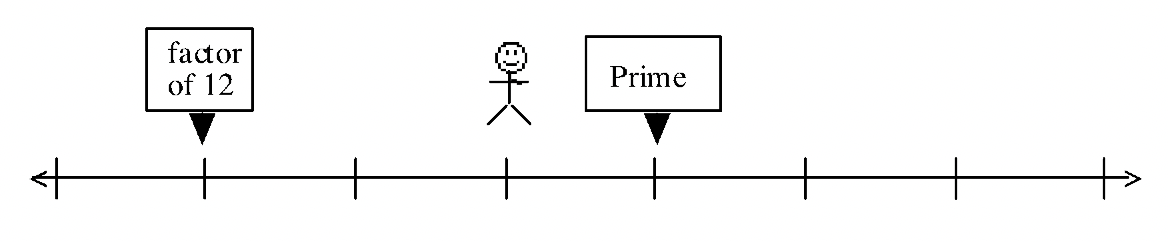


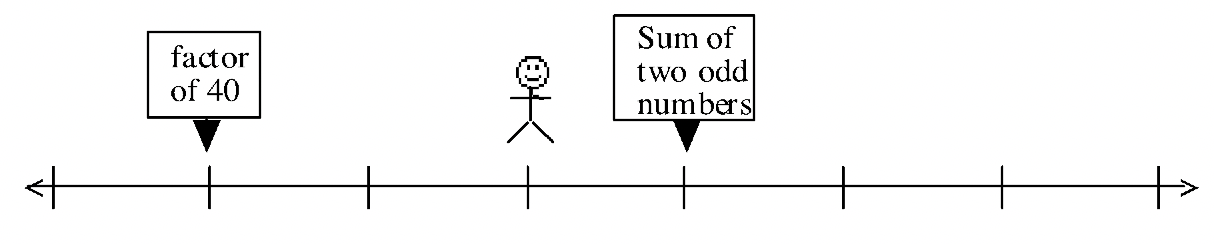
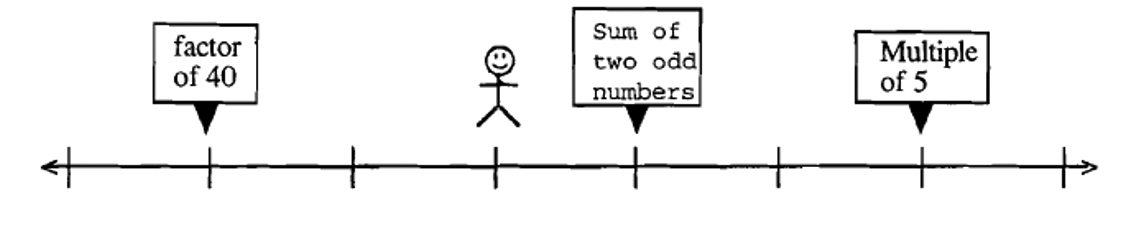
(En realidad hay nueve posibilidades entre 1 y 1000 para este problema.)


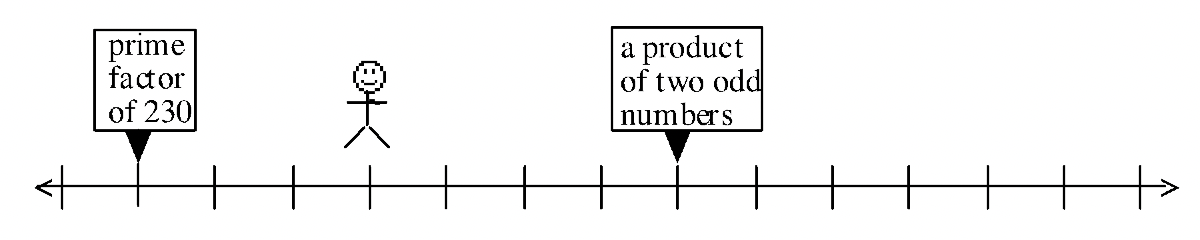
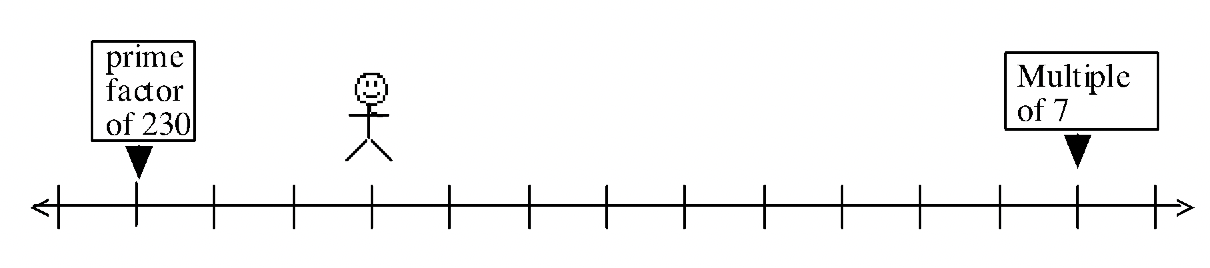
¿Cuál de las pistas en #53 no era necesaria si el hombre sólo está parado sobre un solo número? #54 y #55 deberían ayudarte a responder a esto. Por ejemplo, si tienes más de una posibilidad para #54 o #55, entonces ese problema no proporcionó suficientes pistas. Para el que daba exactamente una posibilidad, ya bastaban pistas, así que la pista del #53 que faltaba no era realmente necesaria.
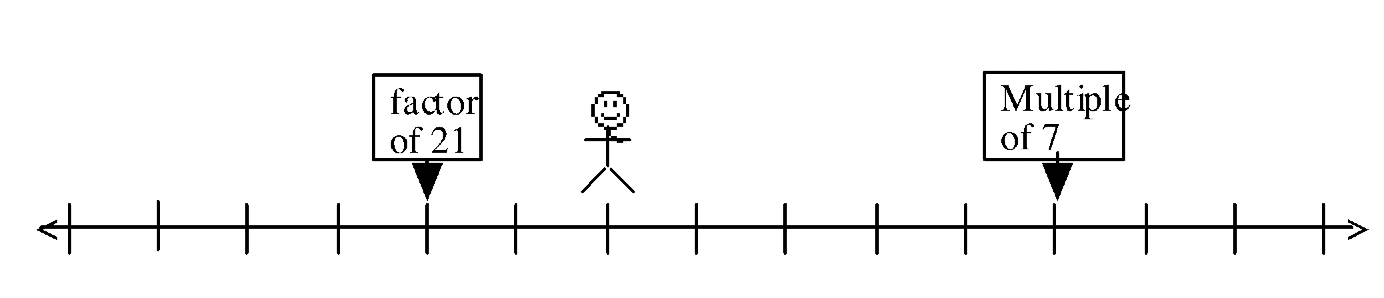


Si el hombre en el ejercicio #59 está parado sobre un solo número en este problema, ¿son necesarias las tres pistas dadas?
Sí o No:_________ Explique:


