2.1: Integral gaussiana revisitada
- Page ID
- 112469
Como primera aplicación, volvamos a revisar la integral gaussiana de la Sección 1.3,
\[\int_{-\infty}^{\infty} e^{-ax^{2}}dx. \label{2.1} \]
¿Es el integral\(\sqrt{\pi α}\) o\(\sqrt{\pi/α}\)?
La elección correcta debe funcionar para todos\(α = 0\). En los puntos finales de este rango (\(α = \infty \text{ and } α = 0\)), la integral es fácil de evaluar.
¿Cuál es la integral cuando\(α = \infty\)?
Como primer caso fácil, aumentar\(α \text{ to } \infty\). Entonces −\(αx^{2}\) se vuelve muy negativo, incluso cuando\(x\) es pequeño. El exponencial de un gran número negativo es pequeño, por lo que la curva de campana se estrecha a una aseta, y su área se reduce a cero. Por lo tanto,\(α \rightarrow \infty\) a medida que la integral se contrae a cero. Este resultado refuta la opción\(\sqrt{\pi α}\), que es infinita cuando\(α = \infty\); y soporta la opción\(\sqrt{\pi/α}\), que es cero cuando\(α = \infty\).
¿Cuál es la integral cuando\(α = 0\)?
En el\(α = 0\) extremo, la curva de campana se aplana en una línea horizontal con altura unitaria. Su área, integrada en el rango infinito, es infinita. Este resultado refuta la\(\sqrt{\pi α}\) opción, que es cero cuando\(α = 0\); y soporta la\(\sqrt{\pi/α}\) opción, que es infinito cuando\(α = 0\). Así, la opción πα falla en ambas pruebas de casos fáciles, y la\(\sqrt{\pi/α}\) opción pasa ambas pruebas de casos fáciles. Si estas dos opciones fueran las únicas, nosotros elegiríamos\(\sqrt{\pi/α}\). No obstante, si una tercera opción fuera\(\sqrt{2/α}\), ¿cómo podrías decidir entre ella y\(\sqrt{\pi/α}\)? Ambas opciones pasan ambas pruebas de casos fáciles; también tienen dimensiones idénticas. La elección parece difícil.
A elegir, prueba un tercer estuche fácil:\(α = 1\). Entonces la integral simplifica a
\[\int_{-\infty}^{\infty} e^{-x^{2}}dx. \label{2.2} \]
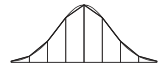
Esta integral clásica se puede evaluar en forma cerrada mediante el uso de coordenadas polares, pero ese método también requiere de un truco con pocas otras aplicaciones (los libros de texto sobre cálculo multivariable dan los detalles grandiosos). Un enfoque menos elegante pero más general es evaluar la integral numéricamente y usar el valor aproximado para adivinar la forma cerrada.
Por lo tanto, reemplace la curva\(e^{−x^{2}}\) suave por una curva que tenga n segmentos de línea. Esta aproximación lineal por tramos convierte el área en una suma de\(n\) trapecios. A medida que
\(n\) se acerca al infinito, el área de los trapecios se acerca cada vez más al área bajo la curva suave.

La tabla da el área bajo la curva en el rango\(x = −10 ... 10\), después de dividir la curva en n segmentos de línea. Las áreas se asientan en un valor estable, y parece familiar. Comienza con 1.7, que podría derivarse de\(\sqrt{3}\). No obstante, continúa como 1.77, que es demasiado grande para serlo\(\sqrt{3}\). Afortunadamente,\(\pi\) es ligeramente mayor que 3, por lo que el área podría estar convergiendo a\(\sqrt{\pi}\).
Comprobemos comparando el área cuadrada con\(\pi\):
1.772453850905522 ≈ 3.14159265358980,
\[\pi ≈ 3.14159265358979. \label{2.3} \]
El encuentro cercano sugiere que la integral\(α = 1\) gaussiana es efectivamente\(\sqrt{π}\):
\[\int_{-\infty}^{\infty} e^{-x^{2}}dx = \sqrt{\pi}. \label{2.4} \]
Por lo tanto, la integral gaussiana general
\[\int_{-\infty}^{\infty} e^{-ax^{2}}dx \label{2.5} \]
debe reducir a\(\sqrt{\pi}\) cuando\(α = 1\). También debe comportarse correctamente en los otros dos casos fáciles\(α = 0 \text{ and } α = \infty\).
Entre las tres opciones\(\sqrt{2/α}\),\(\sqrt{\pi/α}\), y\(\sqrt{\pi α}\), sólo\(\sqrt{\pi/α}\) pasa las tres pruebas\(α = 0, 1, \text{ and } \infty\). Por lo tanto,
\[\int_{-\infty}^{\infty} e^{-ax^{2}}dx = \sqrt{\frac{\pi}{a}}. \label{2.6} \]
Los casos fáciles no son la única manera de juzgar estas elecciones. El análisis dimensional, por ejemplo, también puede restringir las posibilidades (Sección 1.3). Incluso elimina opciones como\(\sqrt{\pi/α}\) esa que pasan las tres pruebas de casos fáciles. Sin embargo, los casos fáciles son, por diseño, simples. No requieren que inventemos o deduzcamos dimensiones para\(x, α\), y dx (el análisis extenso de la Sección 1.3). Los casos fáciles, a diferencia del análisis dimensional, también pueden eliminar opciones como\(\sqrt{2/α}\) con las dimensiones correctas. Cada herramienta tiene sus fortalezas.
Problema 2.1 Probando varias alternativas
Para la integral gaussiana
\[\int_{-\infty}^{\infty} e^{-ax^{2}}dx, \label{2.7} \]
utilizar las tres pruebas de casos fáciles para evaluar su valor a los siguientes candidatos.
(a)\(\sqrt{\pi/α}\)
(b) 1+ (\(\sqrt{\pi}\)−1) /α
(c) 1/α\(^{2}\) + (\(\sqrt{\pi}\)−1) /α.
Problema 2.2 Plausible, alternativa incorrecta
¿Existe una alternativa a\(\sqrt{\pi/α}\) que tenga dimensiones válidas y pase las tres pruebas de casos fáciles?
Problema 2.3 Adivinar un formulario cerrado
Usa un cambio de variable para mostrar que
\[\int_{0}^{\infty} \frac{dx}{1 + x^{2}} = 2\int_{0}^{1} \frac{dx}{1 + x^{2}}. \label{2.8} \]
La segunda integral tiene un rango de integración finito, por lo que es más fácil de evaluar numéricamente que la primera integral. Estime la segunda integral usando la aproximación trapezoidal y una calculadora computacional o programable. Entonces adivina una forma cerrada para la primera integral.


