2.3: Geometría Sólida - El Volumen de una Pirámide Truncada
- Page ID
- 112480
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El ejemplo gaussiano-integral (Sección 2.1) y el ejemplo de elipse área (Sección 2.2) mostraron casos fáciles como método de análisis: para verificar si las fórmulas son correctas. El siguiente nivel de sofisticación es utilizar los casos fáciles como método de síntesis: para construir fórmulas.
Como ejemplo, toma una pirámide con una base cuadrada y corta una pieza desde su parte superior usando un cuchillo paralelo a la base. Esta pirámide truncada (llamada tronco) tiene una base cuadrada y una parte superior cuadrada paralela a la base. Que h sea su altura vertical,\(b\) sea la longitud lateral de su base, y\(a\) sea la longitud lateral de su parte superior.
¿Cuál es el volumen de la pirámide truncada?
Sintetiquemos la fórmula para el volumen. Es una función de las tres longitudes\(h, a, \text{ and } b\). Estas longitudes se dividen en dos tipos: altura y longitud base. Por ejemplo, voltear el sólido sobre su cabeza intercambia los significados de\(a \text{ and } b\) pero preserva\(h\); y ninguna operación simple intercambia la altura con\(a \text{ or } b\). Así, el volumen probablemente tiene dos factores, cada uno conteniendo una longitud o longitudes de un solo tipo:
\[V(h, a, b) = f(h) × g(a, b). \label{2.9} \]
El razonamiento proporcional determinará un\(f; a\) poco de razonamiento dimensional y muchos razonamientos fáciles determinarán\(g\).
Qué es\(f\): ¿Cómo debe depender el volumen de la altura?
Para encontrar\(f\), utilizar un experimento de pensamiento proporcional-razonamiento. Picar el sólido en astillas verticales, cada una como un núcleo de perforación de petróleo; luego imagínese duplicar\(h\). Este cambio duplica el volumen de cada astillas y por lo tanto duplica todo el volumen\(V\). Así\(f ∼ h\) y\(V ∝ h\):
\[V = h \times g(a, b). \label{2.10} \]
Qué es\(g\): ¿De qué depende el volumen\(a \text{ and } b\)?
Debido a que V tiene dimensiones de\(L^{3}\), la función\(g(a, b)\) tiene dimensiones de\(L^{2}\). Esa restricción es todo lo que el análisis dimensional puede decir. Se necesitan más restricciones para sintetizar\(g\), y estas restricciones son proporcionadas por el método de casos fáciles.
Casos fáciles
¿Cuáles son los casos fáciles de\(a \text{ and } b\)?
El caso más fácil es el caso extremo\(a = 0\) (una pirámide ordinaria). La simetría entre a y b sugiere otros dos casos fáciles, a saber\(a = b\), el caso extremo\(b = 0\). Los casos fáciles son entonces triples:
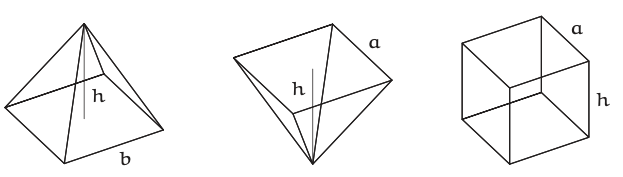
\(a = 0\)\(b = 0\)\(c = 0\)
Cuando\(a = 0\), el sólido es una pirámide ordinaria, y\(g\) es una función solo de la longitud del lado de la base\(b\). Porque\(g\) tiene dimensiones de\(L^{2}\), la única posibilidad para\(g\) es\(g ∼ b\); además,\(V ∝ h\); entonces,\(V ∼ hb^{2}\). Cuando\(b = 0\), el sólido es una versión invertida de la\(b = 0\) pirámide y por lo tanto tiene volumen\(V ∼ ha^{2}\). Cuando a = b, el sólido es un prisma rectangular que tiene volumen\(V = ha^{2}\) (o\(hb^{2}\)).
¿Existe una fórmula de volumen que satisfaga las tres restricciones de casos fáciles?
Las\(b = 0\) restricciones\(a = 0\) y son satisfechas por la suma simétrica\(V ∼ h(a^{2} + b^{2})\). Si la constante adimensional que falta es 1/2\(V = h(a^{2} + b^{2})/2\), haciendo, entonces el volumen también satisface la\(a = b\) restricción, y el volumen de una pirámide ordinaria\((a = 0)\) sería\(hb^{2}/2\).
¿Cuándo\(a = 0\) es\(V = hb^{2}/2\) correcta la predicción?
Probar la predicción requiere encontrar la constante adimensional exacta en\(V ∼ hb^{2}\). Esta tarea parece un problema de cálculo: Rebanar una pirámide en secciones horizontales delgadas y agregar (integrar) sus volúmenes. Sin embargo, una alternativa simple es volver a aplicar estuches fáciles.
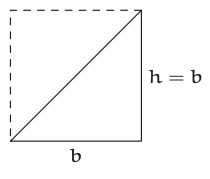
El caso fácil es más fácil de construir después de resolver un problema similar pero más simple: encontrar el área de un triángulo con base\(b\) y altura\(h\). El área satisface\(A ∼ hb\), pero ¿cuál es la constante adimensional? Para encontrarlo, elige b y h para hacer un triángulo fácil: un triángulo rectángulo con\(h = b\). Dos de esos triángulos hacen de 2 una forma fácil: un cuadrado con área\(b\). Así, cada triángulo rectángulo tiene área\(A = b^{2}/2\); la constante adimensional es 1/2. Ahora extiende este razonamiento a tres dimensiones encontrar una pirámide ordinaria (con una base cuadrada) que combina consigo misma para hacer un sólido fácil.
¿Cuál es el sólido fácil?
Un sólido conveniente es sugerido por la base cuadrada de la pirámide: Quizás cada base sea una cara de un cubo. El cubo requiere entonces seis pirámides cuyas puntas se encuentran en el centro del cubo; así las pirámides tienen la relación de aspecto\(h = b/2\). Por simplicidad numérica, vamos a cumplir con esta condición con\(b = 2\) y\(h = 1\).
Seis de esas pirámides forman un cubo con volumen\(b^{3} = 8\), por lo que el volumen de una pirámide es 4/3. Porque cada pirámide tiene volumen\(V ∼ hb^{2}\), y\(hb^{2} = 4\) para estas pirámides, la constante adimensional en\(V ∼ hb^{2}\) debe ser 1/3. El volumen de una pirámide ordinaria (una pirámide con\(a = 0\)) es por lo tanto\(V = hb^{2}/3\).
Adivina el volumen de una pirámide con altura h y una base triangular del área A. Supongamos que el vértice superior se encuentra directamente sobre el centroide de la base. Entonces prueba Problema 2.8.
Las seis pirámides no forman un cubo a menos que el vértice superior de cada pirámide se encuentre directamente por encima del centro de la base. Por lo tanto, el resultado\(V = hb^{2}/3\) podría aplicarse sólo con esta restricción. Si en cambio el vértice superior se encuentra por encima de uno de los vértices base, ¿cuál es el volumen?
La predicción de las tres primeras pruebas de casos fáciles fue\(V = hb^{2}/2\) (cuándo\(a = 0\)), mientras que el caso más fácil\(h = b/2\) junto\(a = 0\) solo lo demostró\(V = hb^{2}/3\). Los dos métodos están haciendo predicciones contradictorias.
¿Cómo se puede resolver esta contradicción?
La contradicción debió haberse colado durante uno de los pasos de razonamiento. Para encontrar al culpable, vuelva a visitar cada paso por turno. El argumento a favor\(V ∝ h\) parece correcto. Los tres requisitos de caso fácil que\(V ∼ hb^{2}\) cuando\(a = 0\), que\(V ∼ ha^{2}\) cuando\(b = 0\), y que\(V = h(a^{2} + b^{2}/2\) cuando\(a = b\) también se ven correctos. El error fue saltando de estas restricciones a la predicción\(V ∼ h(a^{2} + b^{2})\) para cualquiera\(a \text{ or } b\).
En su lugar, probemos la siguiente forma general que incluye un\(ab\) término:
\[V = h(αa^{2} + βab + γb^{2}). \label{2.11} \]
Luego resuelve los coeficientes\(α, β, \text{ and } γ\) volviendo a aplicar los requisitos de casos fáciles.
La\(b = 0\) prueba junto con el caso\(h = b/2\) fácil, que demostró que\(V = hb^{2}/3\) para una pirámide ordinaria, requieren eso\(α = 1/3\). De manera similar, la\(a = 0\) prueba lo requiere\(γ = 1/3\). Y la\(a = b\) prueba lo requiere\(α + β + γ = 1\). Por lo tanto\(β = 1/3\) y voilà,
\[V = \frac{1}{3}h(a^{2} + ab + b^{2}). \label{2.12} \]
Esta fórmula, resultado del razonamiento proporcional, análisis dimensional, y el método de casos fáciles, es exacta (¡Problema 2.9)!
Problema 2.9 Integración
Usa la integración para demostrarlo\(V = h(a^{2} + ab + b^{2})/3\).
Problema 2.10 Pirámide triangular truncada
En lugar de una pirámide con base cuadrada, comience con una pirámide con un triángulo equilátero de longitud lateral b como base. Después haz el sólido truncado cortando una pieza desde la parte superior usando un cuchillo paralelo a la base. En cuanto a la altura h y las longitudes de los lados superior e inferior\(a \text{ and } b\), ¿cuál es el volumen de este sólido? (Ver también Problema 2.7.)
Problema 2.11 Cono truncado
¿Cuál es el volumen de un cono truncado con una base circular de radio\(r_{1}\) y una parte superior circular de radio\(r_{2}\) (con la parte superior paralela a la base)? Generaliza tu fórmula al volumen de una pirámide truncada con altura\(h\), una base de forma y área arbitrarias\(A_{base}\), y una parte superior de área correspondiente\(A_{top}\).