3.2: Estimación de Integrales
- Page ID
- 112601
La curva poblacional estadounidense (Sección 3.1) fue difícil de integrar en parte porque era desconocida. Pero incluso funciones conocidas pueden ser difíciles de integrar. En tales casos, son particularmente útiles dos métodos de aglutinación: la\(1/e\) heurística (Sección 3.2.1) y la heurística de ancho completo a la mitad máxima (FWHM) (Sección 3.2.2).
heurística
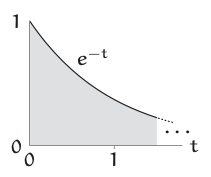
Los circuitos electrónicos, la presión atmosférica y la desintegración radiactiva contienen el exponencial ubicuo y su integral (dado aquí en forma adimensional)
\[\int_{0}^{\infty} e^{-t} dt. \label{3.4} \]
Para aproximar su valor, vamos a abultar la\(e^{−t}\) curva en un rectángulo.
¿Qué valores deben elegirse para el ancho y alto del rectángulo?
Una altura razonable para el rectángulo es la máxima de\(e^{−t}\), a saber, 1. Para elegir su ancho, use el cambio significativo como criterio (método utilizado nuevamente en la Sección 3.3.3): Elija un cambio significativo en\(e^{−t}\); luego busque el ancho\(Δt\) que produce este cambio. En una decadencia exponencial, un cambio significativo simple y natural es cuando\(e^{−t}\) se convierte en un factor\(e\) más cercano a su valor final (que es 0 aquí porque\(t\) va a\(\infty\)). Con este criterio,\(Δt = 1\). El rectángulo de grumado entonces tiene área de unidad, ¡que es el valor exacto de la integral!
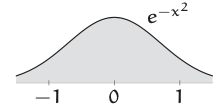
Alentados por este resultado, probemos la heurística sobre la integral difícil
\[\int_{-\infty}^{\infty} e^{-x^{2}}dx. \label{3.5} \]
Nuevamente abulta el área en un solo rectángulo. Su altura es la máxima de\(e^{−x^{2}}\), que es 1. Su ancho es suficiente que\(e^{−x^{2}}\) cae por un factor de\(e\). Esta caída ocurre en\(x = ±1\), por lo que el ancho es\(Δx = 2\) y su área es\(1 \times 2\). El área exacta es\(\sqrt{\pi} ≈ 1.77\) (Sección 2.1), por lo que la formación de grumos produce un error de sólo 13%: Para una derivación tan corta, la precisión es extremadamente alta.
Utilice la formación de grumos para estimar la integral
\[\int_{0}^{\infty} e^{-at}dt. \label{3.6} \]
Utilice el análisis dimensional y los casos fáciles para verificar que su respuesta tenga sentido.
Problema 3.5 Presión atmosférica
La densidad atmosférica\(ρ\) decae aproximadamente exponencialmente con la altura\(z\):
\[ρ ∼ ρ_oe^{-z/H}, \label{3.7} \]
donde\(ρ_0\) es la densidad al nivel del mar, y\(H\) es la llamada altura de escala (la altura a la que la densidad cae por un factor de e). Usa tu experiencia diaria para estimar\(H\).
Después, estime la presión atmosférica a nivel del mar estimando el peso de un cilindro de aire infinitamente alto.
Problema 3.6 Distancia de caída libre del cono
Aproximadamente, ¿hasta qué punto cae un cono de la Sección 2.4 antes de alcanzar una fracción significativa de su velocidad terminal? ¿Qué tan grande es esa distancia en comparación con la altura de caída de 2m? Sugerencia: Esboza (de manera muy aproximada) la aceleración del cono versus el tiempo y haz una aproximación de grumos.
Ancho completo a la mitad como máximo
Otra heurística de grumos razonable surgió en los primeros días de la espectroscopia. A medida que un espectroscopio recorría un rango de longitudes de onda, un registrador gráfico representaría la intensidad con la que una molécula absorbía la radiación de esa longitud de onda. Esta curva contiene muchos picos cuya ubicación y área revelan la estructura de la molécula (y fueron esenciales en el desarrollo de la teoría cuántica [14]). Pero décadas antes de que existieran los grabadores de gráficos digitales, ¿cómo podrían calcularse las áreas de los picos?
Se computaron aglutinando el pico en un rectángulo cuya altura es la altura del pico y cuyo ancho es el ancho completo a la mitad del máximo (FWHM). Cuando la\(1/e\) heurística utiliza un factor de e como cambio significativo, la heurística FWHM utiliza un factor de 2.
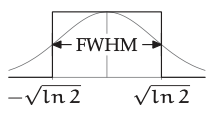
Prueba esta receta en la integral gaussiana\(\int_{-\infty}^{infty} e^{-x^{2}}dx.\) La altura máxima de\(e^{−x^{2}}\) es 1, por lo que los medios máximos están en\(x=± ln2\) y el ancho completo es 2\(\sqrt{ln2}\). Por lo tanto, el rectángulo agrupado tiene área 2\(\sqrt{ln2} ≈ 1.665\). El área exacta es\(\sqrt{\pi} ≈ 1.77\) (Sección 2.1): La heurística FWHM comete un error de sólo 6%, que es aproximadamente la mitad del error de la\(1/e\) heurística.
Hacer estimaciones de agrupamiento de un solo rectángulo de las siguientes integrales. Elija la altura y el ancho del rectángulo usando la heurística FWHM. ¿Qué tan precisa es cada estimación?
- \(\int_{-\infty}^{infty} \frac{1}{1 + x^{2}}dx\)[valor exacto:\(\pi\)]
- \(\int_{-\infty}^{infty} e^{-x^{4}} dx \)[valor exacto: γ (1/4) /2 ≈ 1.813].
Aproximación de Stirling
La heurística de aglutinación\(1/e\) y FWHM siguiente nos ayudan a aproximar la ubicua función factorial n! ; los usos de esta función van desde la teoría de probabilidad hasta la mecánica estadística y el análisis de algoritmos. Para enteros positivos, n! se define como\(n \times (n − 1) \times (n − 2) \times ··· \times 2 \times 1\). En esta forma discreta, es difícil de aproximar. Sin embargo, la representación integral para n! ,
\[n! ≡ \int_{0}^{\infty} t^{n}e^{-t}dt, \label{3.8} \]
proporciona una definición incluso cuando n no es un número entero positivo y este intgeral se puede aproximar usando la formación de grumos. El análisis de aglutinación generará casi toda la famosa fórmula de aproximación de Stirling
\[n! ≈ n^{n}e^{-n}\sqrt{2 \pi n}. \label{3.9} \]
La formación de grumos requiere un pico, pero ¿el integrando\(t^{n}\) e\(^{−t}\) tiene un pico?
Para entender el integrando\(t^{n}e^{−t}\) o\(t^{n}/e^{t}\), examinar los casos extremos de t. Cuando\(t = 0\), el integrando es 0. En el extremo opuesto,\(t \rightarrow \infty\), el factor polinómico tn hace que el producto sea infinito mientras que el factor exponencial lo\(e^{−t}\) hace cero. ¿Quién gana esa lucha? La serie Taylor para et contiene cada potencia de t (y con coeficientes positivos), por lo que es un polinomio creciente de infinitos grados. Por lo tanto, a medida que t va al infinito, et supera cualquier polinomio tn y hace que el integrando tn/et sea igual a 0 en el\(t \rightarrow \infty\) extremo. Al ser cero en ambos extremos, el integrando debe tener un pico intermedio. De hecho, tiene exactamente un pico. (¿Se puede demostrar eso?)
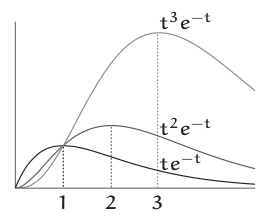
El aumento de n fortalece el factor polinomial\(t^{n}\), por lo que\(t^{n}\) sobrevive hasta una t superior antes de et outruns él. Por lo tanto, el pico de\(t^{n}/e^{t}\) cambios a la derecha a medida que n aumenta. El gráfico confirma esta predicción y sugiere que el pico ocurre en\(t = n\). Comprobemos usando cálculo para maximizar\(t^{n}e^{-t}\) o, más simplemente, para maximizar su logaritmo\(f(t) = n ln t − t\). En un pico, una función tiene pendiente cero. Porque\(df/dt = n/t−1\), el pico ocurre en\(t_{\text{peak}} = n\), cuando el integrando\(t^{n}e^{-t}\) está reproduciendo\(n^{n}e^{-n}\) así el factor más grande e importante en la fórmula de Stirling.
¿Qué es un rectángulo de agrupamiento razonable?
La altura del rectángulo es la altura del pico\(n^{n}e^{-n}\). Para el ancho del rectángulo, use la heurística\(1/e\) o la FWHM. Debido a que ambas heurísticas requieren aproximarse\(t^{n}e^{-t}\), expanden su logaritmo\(f(t)\) en una serie Taylor alrededor de su pico en\(t = n\):
\[f(n+\Delta t)=f(n)+\left.\Delta t \frac{d f}{d t}\right|_{t=n}+\left.\frac{(\Delta t)^{2}}{2} \frac{d^{2} f}{d t^{2}}\right|_{t=n}+\cdots\label{3.10} \]
El segundo término de la expansión Taylor desaparece porque\(f(t)\) tiene pendiente cero en el pico. En el tercer término, la segunda derivada\(d^{2}f/dt^{2}\) at\(t = n\) es\(−n/t^{2}\) o\(−1/n\). Por lo tanto,
Disminuir\(t^{n}e^{−t}\) por un factor de\(F\) requiere disminuir\(f(t)\) por\(lnF\). Esta elección significa\(Δt = \sqrt{2nlnF}\). Debido a que el ancho del rectángulo es\(2Δt\), la estimación de área abultada de\(n!\) es
\ [n! \ sim n^ {n} e^ {-n}\ sqrt {n}\ veces\ izquierda\ {\ begin {array} {ll}
\ sqrt {8} & (1/e\ text {criterio:} f=E)\\
\ sqrt {8\ ln 2} &\ text {(criterio FWHM:} F=2\ text {).}
\ end {array}\ right. \ label {3.12}\]
A modo de comparación, la fórmula de Stirling es\(n! ≈ n^{n}e^{−n}\)\(\sqrt{2\pi n}\). La formación de grumos ha explicado casi todos los factores. El\(n^{n}e^{−n}\) factor es la altura del rectángulo, y el\(\sqrt{n}\) factor es del ancho del rectángulo. Aunque el\(\sqrt{2\pi}\) factor exacto sigue siendo misterioso (Problema 3.9), se aproxima a dentro del 13% (la\(1/e\) heurística) o 6% (la heurística FWHM).
Problema 3.8 ¿Coincidencia?
La aproximación FWHM para el área bajo un Gaussiano (Sección 3.2.2) también fue exacta al 6%. ¿Coincidencia?
Problema 3.9 Constante exacta en la fórmula de Stirling
¿De dónde\(\sqrt{2\pi}\) viene el factor constante más preciso de?


