3.4: Análisis de ecuaciones diferenciales- El sistema de masa de resorte
- Page ID
- 112588
Estimar derivadas reduce la diferenciación a división (Sección 3.3); con ello reduce las ecuaciones diferenciales a ecuaciones algebraicas.
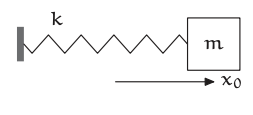
Para producir una ecuación de ejemplo para analizar, conecte un bloque de masa m a un resorte ideal con constante de resorte (rigidez)\(k\), tire del bloque una distancia\(x_{0}\) hacia la derecha en relación con la posición\(x = 0\) de equilibrio y libérelo en el momento\(t = 0\). El bloque oscila hacia adelante y hacia atrás, su posición\(x\) descrita por la ecuación diferencial ideal-resorte
\[m\frac{d^{2}x}{dt^{2}}+kx = 0. \label{3.21} \]
Vamos a aproximar la ecuación y con ello estimar la frecuencia de oscilación.
Comprobando dimensiones
Al ver cualquier ecuación, primero verifique sus dimensiones (Capítulo 1). Si todos los términos no tienen dimensiones idénticas, la ecuación no vale la pena resolver un gran ahorro de esfuerzo. Si las dimensiones coinciden, la comprobación ha suscitado una reflexión sobre el significado de los términos; esta reflexión ayuda a prepararse para resolver la ecuación y para entender cualquier solución.
¿Cuáles son las dimensiones de los dos términos en la ecuación de primavera?
Mira primero el sencillo segundo término\(kx\). Surge de la ley de Hooke, que dice que un resorte ideal ejerce una fuerza\(kx\) donde\(x\) está la extensión del resorte con relación a su longitud de equilibrio. Así, el segundo término\(kx\) es una fuerza. ¿El primer término también es una fuerza?
El primer término m (d\(^{2}\) x/dt\(^{2}\)) contiene la segunda derivada\(d^{2}x/dt^{2}\), la cual es familiar como aceleración. Muchas ecuaciones diferenciales, sin embargo, contienen derivadas desconocidas. Las ecuaciones Navier-Stokes de la mecánica de fluidos (Sección 2.4),
\[\frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v} \cdot \boldsymbol{\nabla}) \mathbf{v}=-\frac{1}{\rho} \boldsymbol{\nabla} p+v \boldsymbol{\nabla}^{2} \mathbf{v}\label{3.22} \]
contienen dos derivados extraños:\((v·∇)v\) y\(∇^{2}v\). ¿Cuáles son las dimensiones de esos términos?
Para practicar para luego manejar términos tan complicados, ahora encontremos las dimensiones de a\(d^{2}x/dt^{2}\) mano. Porque\(d^{2}x/dt^{2}\) contiene dos exponentes de 2, y\(x\) es longitud y t es tiempo,\(d^{2}x/dt^{2}\) podría tener plausiblemente dimensiones de\(L^{2}T^{2}\).
¿Son\(L^{2}T^{-2}\) las dimensiones correctas?
Para decidir, use la idea de la Sección 1.3.2 de que el símbolo diferencial d significa “un poco de”. El numerador\(d^{2}x\), que significa\(d\) dx, es “un poco de un poquito de x”. Por lo tanto, es una longitud. El denominador\(dt^{2}\) podría significar plausiblemente\((dt)^{2}\) o\(d(t^{2}\)). [Resulta que significa\((dt)^{2})\). En cualquier caso, sus dimensiones son\(T^{2}\). Por lo tanto, las dimensiones de la segunda derivada son\(LT^{-2}\):
\[[\frac{d^{2}}{dt^{2}}] = LT^{-2}\label{3.23} \]
Esta combinación es una aceleración, por lo que el primer término de la ecuación de resorte\(m(d^{2}x/dt^{2})\) es masa por aceleración dándole las mismas dimensiones que el\(kx\) término.
¿Cuáles son las dimensiones de la constante de resorte\(k\)?
Estimación de las magnitudes de los términos
La ecuación de resorte pasa la prueba de dimensiones, por lo que vale la pena analizarla para encontrar la frecuencia de oscilación. El método consiste en sustituir cada término con su magnitud aproximada. Estos reemplazos convertirán una complicada ecuación diferencial en una ecuación algebraica simple para la frecuencia.
Para aproximar el primer término\(m(d^{2}x/dt^{2})\), utilice la aproximación de cambio significativo (Sección 3.3.3) para estimar la magnitud de la aceleración\(d^{2}x/dt^{2}\).
\[\frac{d^{2}x}{dt^{2}} ∼ \frac{\text{ significant Δx }}{\text{ (Δt that produces a significant Δx m)}^{2}}. \label{3.24} \]
El numerador contiene sólo la primera potencia de\(Δx\), mientras que el denominador contiene la segunda potencia de\(Δt\). ¿Cómo puede ser correcta esa discrepancia?
Para evaluar esta aceleración aproximada, primero decidir sobre un significativo\(Δx\) sobre lo que constituye un cambio significativo en la posición de la masa.
La masa se mueve entre los puntos\(x = −x_{0}\) y\(x = +x_{0}\), por lo que un cambio significativo en la posición debe ser una fracción significativa de la amplitud pico a pico\(2x_{0}\). La elección más sencilla es\(Δx = x_{0}\). Ahora estime\(Δt\): el tiempo para que el bloque se mueva una distancia comparable a\(Δx\). Este tiempo llamado el tiempo característico del sistema está relacionado con el período de oscilación T. Durante un período, la masa se mueve hacia adelante y hacia atrás y recorre una distancia\(4x_{0}\) mucho más lejos que\(x_{0}\). Si\(Δt\) fuera, digamos,\(T/4\) o\(T/2\pi\), entonces en el tiempo\(Δt\) la masa recorrería una distancia comparable a\(x_{0}\). Esas elecciones para\(Δt\) tienen una interpretación natural como siendo aproximadamente\(1/ω\), donde la frecuencia angular\(ω\) está conectada al periodo por la definición\(ω ≡ 2\pi/T\). Con las opciones anteriores para\(Δx\) y\(Δt\), el\(m(d^{2}x/dt^{2})\) término es aproximadamente\(mx_{0}ω^{2}\).
¿Qué significa “es aproximadamente”?
La frase no puede significar eso\(mx_{0}ω^{2}\) y\(m(d^{2}x/dt^{2})\) están dentro, digamos, de un factor de 2, porque\(m(d^{2}x/dt^{2})\) varía y\(mx_{0}/τ^{2}\) es constante. Más bien, “es aproximadamente” significa que una magnitud típica o característica de,\(m(d^{2}x/dt^{2})\) por ejemplo, su valor cuadrático medio es comparable a\(mx_{0}ω^{2}\). Incluyamos este significado dentro de la notación twiddle ∼. Entonces se puede escribir la estimación de magnitud típica
Con el mismo significado de “es aproximadamente”, es decir, que las magnitudes típicas son comparables, el segundo término de la ecuación de primavera kx es aproximadamente\(kx_{0}\). Los dos términos deben sumar a cero una consecuencia de la ecuación de resorte
\[m\frac{d^{2}x}{dt^{2}} + kx = 0. \label{3.26} \]
Por lo tanto, las magnitudes de los dos términos son comparables:
\[mx_{0}w^{2} ∼ kx_{0}. \label{3.27} \]
¡La amplitud se\(x_{0}\) divide! Con\(x_{0}\) ido, la frecuencia ω y el período de oscilación\(T = 2\pi/ω\) son independientes de la amplitud. [Este razonamiento utiliza varias aproximaciones, pero esta conclusión es exacta (Problema 3.20).] La frecuencia angular aproximada\(ω\) es entonces\(\sqrt{k/m}\).
A modo de comparación, la solución exacta de la ecuación diferencial de resorte es, del Problema 3.22,
\[x = x_{0} cos ωt, \label{3.28} \]
donde\(ω\) esta\(\sqrt{k/m}\). ¡La frecuencia angular aproximada también es exacta!
Problema 3.20 Independencia de amplitud
Utilice el análisis dimensional para mostrar que la frecuencia angular\(ω\) no puede depender de la amplitud\(x_{0}\).
Problema 3.21 Comprobando dimensiones en la supuesta solución
¿Cuáles son las dimensiones de\(ωt\)? ¿Cuáles son las dimensiones de\(\cos ωt\)? Consultar las dimensiones de la solución propuesta\(x = x \cos ωt\), y las dimensiones del periodo propuesto\(2\pi \sqrt{m/k}\).
Problema 3.22 Verificación
Demostrar que\(x = x_{0} \cos ωt\) con\(ω = \sqrt{k/m}\) resuelve la ecuación diferencial de resorte
\[m\frac{d^{2}x}{dt^{2}}+kx = 0. \label{3.29} \]
Significado del número de Reynolds
Como otro ejemplo de agrupamiento en particular, de la aproximación de cambio significativo analicemos las ecuaciones Navier-Stokes introducidas en la Sección 2.4,
\[\frac{\partial \mathbf{v}}{\partial t}+(\mathbf{v} \cdot \boldsymbol{\nabla}) \mathbf{v}=-\frac{1}{\rho} \boldsymbol{\nabla} p+v \boldsymbol{\nabla}^{2} \mathbf{v} \label{3.30} \]
y extraer de ellos un significado físico para el número de Reynolds\(rv/ν\).
Para ello, estimamos la magnitud típica del término inercial\((v·∇)v\) y del término viscoso\(ν∇^{2}v\).
¿Cuál es la magnitud típica del término inercial?
El término inercial\((v·∇)v\) contiene la derivada espacial\(∇v\). Según la aproximación de cambio significativo (Sección 3.3.3), la derivada\(∇v\) es aproximadamente la relación
\[\frac{\text{ significant change in flow velocity }}{\text{ distance over which flow velocity changes significantly }}. \label{3.31} \]
La velocidad de flujo (la velocidad del aire) es casi cero lejos del cono y es comparable a v cerca del cono (que se mueve a velocidad v). Por lo tanto, v, o una fracción razonable de\(v\), constituye un cambio significativo en la velocidad del flujo. Este cambio de velocidad ocurre en una distancia comparable al tamaño del cono: Varias longitudes de cono de distancia, el aire apenas sabe sobre el cono que cae. Así\(∇v ∼ v/r\). El término inercial\((v·∇)v\) contiene un segundo factor de\(v\), así\((v·∇)v\) es más o menos\(v^{2}/r\).
¿Cuál es la magnitud típica del término viscoso?
El término viscoso\(ν∇^{2}v\) contiene dos derivados espaciales de\(v\).
Debido a que cada derivada espacial aporta un factor de\(1/r\) a la magnitud típica,\(ν∇^{2}v\) es aproximadamente\(νv/r^{2}\). La relación entre el término inercial y el término viscoso es entonces aproximadamente\((v^{2}/r)/(νv/r^{2})\). Esta relación simplifica a rv/ν el familiar, adimensional, número de Reynolds.
Así, el número de Reynolds mide la importancia de la viscosidad. Cuando\(Re\) ≫ 1, el término viscoso es pequeño y la viscosidad tiene un efecto insignificante. No puede evitar que los trozos de fluido cercanos adquieran velocidades significativamente diferentes, y el flujo se vuelve turbulento. Cuando\(Re\) 1, el término viscoso es grande, y la viscosidad es el efecto físico dominante. El flujo rezuma, como al verter miel fría.


