4.4: Bisecar un Triángulo
- Page ID
- 112488
Las soluciones pictóricas son especialmente probables para un problema geométrico:
¿Cuál es el camino más corto que divide un triángulo equilátero en dos regiones de igual área?
Los posibles caminos bisecantes forman un conjunto infinitamente infinito. Para manejar la complejidad, prueba casos fáciles (Capítulo 2) dibuja algunos triángulos equiláteros y los bisecciona con caminos fáciles. Podrían surgir patrones, ideas o incluso una solución.
¿Cuáles son algunos caminos fáciles?
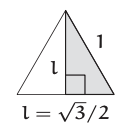
El camino de bisección más simple es un segmento vertical que divide el triángulo en dos triángulos rectos cada uno con base 1/2. Este camino es la altitud del triángulo, y tiene longitud
\[l = \sqrt{1^{2} - (1/2)^{2} = \frac{\sqrt{3}}{2} ≈ 0.866. \label{4.42} \]
Un camino recto alternativo divide el triángulo en un trapecio y un triángulo pequeño.
¿Cuál es la forma del triángulo más pequeño y cuánto dura el camino?
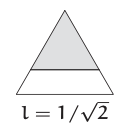
El triángulo es similar al triángulo original, por lo que también es equilátero. Además, tiene la mitad del área del triángulo original, por lo que sus tres lados, uno de los cuales es el camino bisectriz, son un factor de\(\sqrt{2}\) menor tamaño que los lados del triángulo original. Por lo tanto, esta trayectoria tiene\(1/\sqrt{2} ≈ 0.707\) una mejora sustancial en la trayectoria vertical con la longitud\(\sqrt{3}/2\).
Un triángulo equilátero tiene infinitamente muchas trayectorias biseccionales de un segmento. Algunos de ellos se muestran en la figura. ¿Cuál ruta de un segmento es la más corta?

Ahora investiguemos caminos fáciles de dos segmentos. Un posible camino encierra un diamante y excluye dos triángulos pequeños. Los dos triángulos pequeños ocupan la mitad de toda el área. Por lo tanto, cada triángulo pequeño ocupa un cuarto de toda el área y tiene una longitud lateral 1/2. Debido a que el camino bisecante contiene dos de estos lados, tiene longitud 1. Este camino es, lamentablemente, más largo que nuestros dos candidatos de un segmento, cuyas longitudes son\(1/\sqrt{2}\) y\(\sqrt{3}/2\).
Por lo tanto, una conjetura razonable es que el camino más corto tiene el menor número de segmentos. Esta conjetura merece ser probada (Problema 4.26).
Problema 4.26 Todas las rutas de dos segmentos
Dibuja una figura que muestre la variedad de trayectorias de dos segmentos. Encuentra el camino más corto, mostrando que tiene longitud
\[l = 2 \times 3^{1/4} x \sin 15^{◦} ≈ 0.681. \label{4.43} \]
Problema 4.27 Bisección con caminos cerrados
El camino de bisección no necesita comenzar o terminar en un borde del triángulo. Aquí se ilustran dos ejemplos:
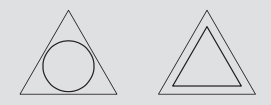
¿Espera que las trayectorias biseccionales cerradas sean más largas o más cortas que la ruta de un segmento más corta? Da una razón geométrica para tu conjetura y verifica la conjetura encontrando las longitudes de los dos caminos cerrados ilustrativos.
¿El uso de menos segmentos produce trayectorias más cortas?
La ruta más corta de un segmento tiene una longitud aproximada de 0.707; pero la ruta de dos segmentos más corta tiene una longitud aproximada de 0.681. La disminución de longitud sugiere probar caminos extremos: caminos con un número infinito de segmentos. En otras palabras, prueba caminos curvos. El camino curvo más fácil es probablemente un círculo o un trozo de círculo.
¿Cuál es un candidato probable para el círculo más corto o la pieza de un círculo que bisecta el triángulo?
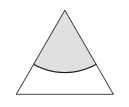
Ya sea que el camino sea un círculo o un trozo de círculo, necesita un centro. Sin embargo, poner el centro dentro del triángulo y usar un círculo completo produce un largo camino bisecante (Problema 4.27). El único otro centro plausible es un vértice del triángulo, así que imagina un arco bisectriz centrado en un vértice.
¿Cuánto dura este arco?
El arco subtiende una sexta parte\((60^{◦})\) del círculo completo, por lo que su longitud es\(l = \pi r/3\), donde r es el radio del círculo completo. Para encontrar el radio, use el requisito de que el arco debe biseccionar el triángulo. Por lo tanto, el arco encierra la mitad del área del triángulo. La condición en r es que\(\pi r^{2} = 3\sqrt{3}/4\):
\[\frac{1}{6} \times \underbrace{\text{area of the full circle}}_{\pi r^{2}} = \frac{1}{2} \times \underbrace{\text{area of the triangle.}}_{\sqrt{3}/4} \label{4.44} \]
El radio es por lo tanto\((3\sqrt{3}/4\pi)^{1/2}\); la longitud del arco es\(\pi r/3\), que es aproximadamente 0.673. Esta trayectoria curva es más corta que la ruta de dos segmentos más corta. Podría ser el camino más corto posible.
Para probar esta conjetura, utilizamos la simetría. Debido a que un triángulo equilátero es una sexta parte de un hexágono, construya un hexágono replicando el triángulo equilátero biseccionado. Aquí está el hexágono construido a partir del triángulo biseccionado por una línea horizontal:
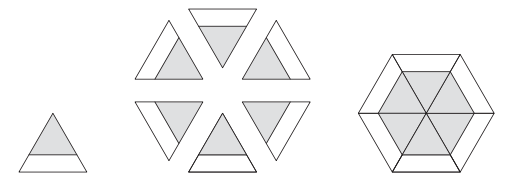
Los seis caminos bisecantes forman un hexágono interno cuya área es la mitad del área del hexágono grande.
¿Qué sucede al replicar el triángulo biseccionado por el arco circular?
Cuando ese triángulo es replicado, sus seis copias forman un círculo con área igual a la mitad del área del hexágono. Para un área fija, un círculo tiene el perímetro más corto (el teorema isoperimétrico [30] y Problema 4.11); por lo tanto, una sexta parte del círculo es el camino de bisección más corto.
Problema 4.28 Replicar la bisección vertical
El triángulo biseccionado por una línea vertical, si se replica y solo se gira, produce una región cerrada fragmentada en lugar de un polígono convexo. ¿Cómo se puede replicar el triángulo para que las seis trayectorias bisectoras formen un polígono regular?
Problema 4.29 Bisecando el cubo
De todas las superficies que bisecan un cubo en dos volúmenes iguales, ¿qué superficie tiene el área más pequeña?


