5.3: Cambios fraccionarios con exponentes generales
- Page ID
- 112528
Las aproximaciones de cambio fraccional para los cambios en\(x^{2}\) (Sección 5.2.3) y en\(x^{3}\) (Problema 5.13) son casos especiales de la aproximación para\(x^{n}\)
\[\frac{Δ(x^{n})}{x^{n}} ≈ n \times \frac{Δx}{x}. \label{5.14} \]
Esta regla ofrece un método para la división mental (Sección 5.3.1), para estimar raíces cuadradas (Sección 5.3.2), y para juzgar una explicación común para las estaciones (Sección 5.3.3). La regla requiere únicamente que el cambio fraccionario sea pequeño y que el exponente n no sea demasiado grande (Sección 5.3.4).
División mental rápida
El caso especial\(n = −1\) proporciona el método para la división mental rápida. A modo de ejemplo, vamos a estimar 1/13. Reescribirlo como\((x + Δx) − 1\) con\(x = 10\) y\(Δx = 3\). La gran parte es\(x − 1 = 0.1\). Porque\((Δx)/x = 30%\), la corrección fraccionaria a\(x − 1\) es aproximadamente − 30%. El resultado es 0.07.
\[frac{1}{13} ≈ \frac{1}{10} − 30% = 0.07, \label{5.15} \]
donde la notación “− 30%”, que significa “disminuir el objeto anterior en un 30%”, es una taquigrafía útil para un factor de\(1 − 0.3\).
¿Qué tan precisa es la estimación y cuál es la fuente del error?
La estimación está en error por sólo 9%. El error surge porque la aproximación lineal
\[\frac{Δx^{-1}}{x^{-1}} ≈ −1 \times \frac{Δx}{x} \label{5.16} \]
no incluye el cuadrado (o potencias superiores) del cambio fraccionario\((Δx)/x\) (Problema 5.17 pide encontrar el término cuadrado).
¿Cómo se puede reducir el error en la aproximación lineal?
Para reducir el error, reducir el cambio fraccional. Debido a que el cambio fraccional está determinado por la gran parte, aumentemos la precisión de la parte grande. En consecuencia, multiplicar 1/13 por 8/8, una forma conveniente de 1, para construir 8/104. Su gran parte 0.08 se aproxima a 1/13 ya a dentro del 4%. Para mejorarlo, escribe 1/104 como\((x + Δx) − 1\) con\(x = 100\) y\(Δx = 4\). El cambio fraccionario\((Δx)/x\) es ahora 0.04 (en lugar de 0.3); y la corrección fraccionaria a\(1/x\) y\(8/x\) es un mero − 4%. La estimación corregida es 0.0768:
\[\frac{1}{13} ≈ 0.08 − 4% = 0.08 − 0.0032 = 0.0768. \label{5.17} \]
¡Esta estimación se puede hacer mentalmente en segundos y es precisa al 0.13%!
Problema 5.16 Siguiente aproximación
Multiplica 1/13 por una forma conveniente de 1 para hacer un denominador cerca de 1000; luego estimar 1/13. ¿Qué tan precisa es la aproximación resultante?
Problema 5.17 Aproximación cuadrática
Encuentra A, el coeficiente del término cuadrático en la aproximación mejorada de cambio fraccional
\[\frac{Δx^{-1}}{x^{-1}} ≈ −1 \times \frac{Δx}{x} + A \times (\frac{Δx}{x})^{2}. \label{5.18} \]
Utilice la aproximación resultante para mejorar las estimaciones para 1/13.
Problema 5.18 Eficiencia de combustible
La eficiencia del combustible es inversamente proporcional al consumo de energía. Si un límite de velocidad de 55 mph disminuye el consumo de energía en un 30%, ¿cuál es la nueva eficiencia de combustible de un automóvil que anteriormente obtenía 30 millas por galón estadounidense (12.8 kilómetros por litro)?
Raíces cuadradas
El exponente fraccional\(n = 1/2\) proporciona el método para estimar raíces cuadradas. A modo de ejemplo, vamos a estimar\(\sqrt{10}\). Reescribirlo como\((x + Δx)^{1/2}\) con\(x = 9\) y\(Δx = 1\). La gran parte\(x^{1/2}\) es 3. Porque\((Δx)/x = 1/9\) y\(n = 1/2\), la corrección fraccionaria es 1/18. La estimación corregida es
\[\sqrt{10} ≈ 3 x (1 + \frac{1}{18}) ≈ 3.1667. \label{5.19} \]
El valor exacto es 3.1622.., por lo que la estimación es exacta a 0.14%.
Problema 5.19 ¿Sobreestimar o subestimar?
¿La aproximación lineal de cambio fraccionario sobreestima todas las raíces cuadradas (ya que sobreestimó 10)? En caso afirmativo, explique por qué; si no, dar un contraejemplo.
Problema 5.20 Aproximación del coseno
Usa la aproximación de ángulo pequeño\(\sin θ ≈ θ\) para mostrar eso\(\cos θ ≈ 1 − θ^{2}/2\).
Problema 5.21 Reduciendo el cambio fraccional
Para reducir el cambio fraccionario al estimar\(\sqrt{10}\), reescribirlo como\(\sqrt{360}/6\) y luego estimar\(\sqrt{360}\). ¿Qué tan precisa es la estimación resultante\(\sqrt{10}\)?
Problema 5.22 Otro método para reducir el cambio fraccional
Porque\(\sqrt{2}\) es fraccionalmente distante de las raíces cuadradas enteras más cercanas\(\sqrt{1}\) y\(\sqrt{4}\), los cambios fraccionarios no dan una estimación directa y precisa de\(\sqrt{2}\). Un problema similar ocurrió en la estimación\(ln2\) (Sección 4.3); ahí, reescribir 2 como (4/3)/(2/3) mejoró la precisión. ¿Esa reescritura ayuda a estimar\(\sqrt{2}\)?
Problema 5.23 Raíz cubo
Estimar\(2^{1/3}\) dentro del 10%.
¿Una razón para las estaciones?
Los veranos son más cálidos que los inviernos, a menudo se alega, porque la tierra está más cerca del sol en verano que en invierno. Esta explicación común es falsa por dos razones. Primero, los veranos en el hemisferio sur ocurren junto a los inviernos en el hemisferio norte, a pesar de casi ninguna diferencia en las respectivas distancias al sol. Segundo, como ahora estimaremos, la distancia tierra-sol variable produce una diferencia de temperatura demasiado pequeña. La cadena causal: que la distancia determina la intensidad de la radiación solar y que la intensidad determina la temperatura de la superficie se analiza más fácilmente mediante cambios fraccionarios.
Intensidad de la radiación solar: La intensidad es la energía solar dividida por el área sobre la que se propaga. La energía solar apenas cambia a lo largo de un año (el sol existe desde hace varios miles de millones de años); sin embargo, a una distancia r del sol, la energía se ha extendido sobre una esfera gigante con superficie\(\text{area} ∼ r^{2}\). Por lo tanto, la intensidad I varía según\(I ∝ r^{-2}\). Los cambios fraccionarios en radio e intensidad están relacionados por
\[\frac{ΔI}{I} ≈ −2 \times \frac{Δr}{r}. \label{5.20} \]
Temperatura superficial: La energía solar entrante no puede acumularse y regresa al espacio como radiación de cuerpo negro. Su intensidad saliente depende de la temperatura T de la superficie terrestre según la ley Stefan—Boltzmann\(I = σT^{4}\) (Problema 1.12), donde σ es la constante Stefan—Boltzmann. Por lo tanto\(T ∝ I^{1/4}\). Usando cambios fraccionarios,
\[\frac{ΔT}{T} ≈ \frac{1}{4} x \frac{ΔI}{I}. \label{5.21} \]
Esta relación conecta intensidad y temperatura. La temperatura y la distancia están conectadas por\((ΔI)/I = −2 \times (Δr)/r\). Cuando se unen, las dos relaciones conectan distancia y temperatura de la siguiente manera:

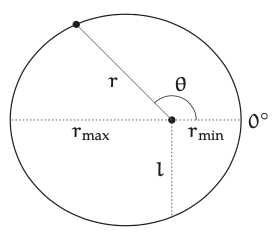
El siguiente paso en el cálculo es estimar la entrada a\((Δr)/r\) saber, el cambio fraccionario en la distancia del sol terrestre. La tierra orbita al sol en una elipse; su distancia orbital es
\[r = \frac{1}{1 + \mathcal{E}\cosθ}, \label{5.22} \]
donde\(\mathcal{E}\) está la excentricidad de la órbita, θ es el ángulo polar, y l es el recto semilato. Así r varía de\(r_{min} = l/(1 + \mathcal{E})\) (cuando\(θ = 0^{◦}\)) a\(r_{max} = l/(1 − \mathcal{E})\) (cuando\(θ = 180^{◦}\)). El incremento de\(r_{min}\) a l aporta un cambio fraccionario de aproximadamente\(\mathcal{E}\). El incremento de l a\(r_{max}\) contribuye otro cambio fraccionario de aproximadamente\(\mathcal{E}\). Así, r varía aproximadamente\(2\mathcal{E}\). Para la órbita terrestre,\(\mathcal{E} = 0.016\), por lo que la distancia tierra-sol varía en 0.032 o 3.2% (haciendo que la intensidad varíe en 6.4%).
Problema 5.24 ¿Dónde está el sol?
El diagrama anterior de la órbita terrestre colocó al sol lejos del centro de la elipse. El diagrama de la derecha muestra el sol en una ubicación alternativa y quizás más natural: en el centro de la elipse. ¿Qué leyes físicas, si las hay, impiden que el sol se asiente en el centro de la elipse?
Problema 5.25 Comprobar el cambio fraccionario
Busque las distancias mínima y máxima tierra-sol y verifique que la distancia sí varía en 3.2% de mínima a máxima. /
Un incremento de 3.2% en la distancia provoca una ligera caída de temperatura:
\[\frac{ΔT}{T} ≈ -\frac{1}{2} x \frac{Δr}{r} = -1.6%. \label{5.23} \]
Sin embargo, el hombre no vive solo de los cambios fraccionarios y experimenta el cambio absoluto de temperatura\(ΔT\).
\[ΔT = −1.6% × T. \lbael{5.24} \nonumber \]
Si nuestro cálculo lo predice\(ΔT ≈ 0^{◦}C\), debe estar equivocado. Una conclusión aún menos plausible resulta de medir\(T\) en grados Fahrenheit, lo que\(T\) a menudo hace negativo en partes del hemisferio norte. Sin embargo, ¡\(ΔT\)no puede voltear su signo solo porque\(T\) se mide en grados Fahrenheit!
Afortunadamente, la escala de temperatura está limitada por la ley Stefan—Boltzmann. Para que el flujo de cuerpo negro sea proporcional a\(T^{4}\), la temperatura debe medirse en relación con un estado con cero energía térmica: cero absoluto. Ni la escala Celsius ni la Fahrenheit cumplen con este requisito.
En contraste, la escala Kelvin sí mide la temperatura relativa al cero absoluto. En la escala Kelvin, la temperatura media de la superficie es\(T ≈ 300 K\); así, un cambio de 1.6% en T hace\(ΔT ≈ 5K\). Un\(5K\) cambio también es un\(5^{◦}C\) cambio Kelvin y grados Celsius son del mismo tamaño, aunque las escalas tienen diferentes puntos cero. (Ver también Problema 5.26.) Un cambio típico de temperatura entre verano e invierno en latitudes templadas es\(20^{◦}C\) mucho mayor que el\(5^{◦}C\) cambio previsto, incluso después de haber permitido errores en la estimación. Una distancia tierra-sol variable es una explicación dudosa de la razón de las estaciones.
La conversión entre las temperaturas Fahrenheit y Celsius es
\[F = 1.8C + 32, \label{5.25} \]
así que un cambio de\(5^{◦}C\) debería ser un cambio de\(41^{◦}F\) lo suficientemente grande como para explicar las estaciones! ¿Qué tiene de malo este razonamiento?
Problema 5.27 Explicación alternativa
Si una distancia variable al sol no puede explicar las estaciones, ¿qué puede? Su propuesta debería, de paso, explicar por qué los hemisferios norte y sur tienen verano con 6 meses de diferencia.
Límites de validez
La aproximación lineal de cambio fraccionario
\[\frac{Δ (x^{n})}{x^{n}} ≈ n x \frac{Δx}{x} \label{5.26} \]
ha sido útil. Pero, ¿cuándo es válido? Para investigar sin ahogarse en la notación, escriba\(z\) para\(Δx\); luego elija\(x = 1\) hacer\(z\) el cambio absoluto y el fraccional. El lado derecho se convierte\(nz\), y la aproximación lineal de cambio fraccional es equivalente a
\[(1+z)^{n} ≈ 1 + nz. \label{5.27} \]
La aproximación se vuelve inexacta cuando\(z\) es demasiado grande: por ejemplo, al evaluar\(1 + z\) con\(z = 1\) (Problema 5.22). ¿El exponente\(n\) también está restringido? Los ejemplos anteriores ilustraron solo exponentes de tamaño moderado:\(n = 2\) para consumo de energía (Sección 5.2.3), −2 para eficiencia de combustible (Problema 5.18), −1 para reciprocales (Sección 5.3.1), 1/2 para raíces cuadradas (Sección 5.3.2) y −2 y 1/4 para las estaciones (Sección 5.3.3). Necesitamos más datos.
¿Qué sucede en el caso extremo de los grandes exponentes?
Con un gran exponente como\(n = 100\) y, digamos,\(z = 0.001\), la aproximación predice que 1.001100 ≈ 1.1 cerca del verdadero valor de 1.105... Sin embargo, elegir lo mismo al\(n\) lado\(z = 0.1\) (mayor que 0.001 pero aún pequeño) produce la terrible predicción
\[\underbrace{1.1^{100}}_{(1+z)^{n}} = 1 + \underbrace{100 x 0.1}_{nz} = 11; \label{5.28} \]
1.1100 es aproximadamente 14,000, más de 1000 veces mayor que la predicción.
Ambas predicciones utilizaron n grande y z pequeña, sin embargo, solo una predicción fue precisa; así, el problema no puede estar en\(n\) o\(z\) solo. Quizás el culpable es el producto adimensional\(nz\). Para probar esa idea, mantén\(nz\) constante mientras intentas grandes valores de\(n\). Para\(nz\), una constante sensible es 1 el número adimensional más simple. Aquí hay varios ejemplos.
\[1.1^{10} ≈ 2.59374, \nonumber \]
\[1.01^{100} ≈ 2.70481, \label{5.29} \]
\[1.001^{100} ≈ 2.71692. \nonumber \]
En cada ejemplo, la aproximación lo predice incorrectamente\((1 + z)^{n} = 2\).
¿Cuál es la causa del error?
Para encontrar la causa, continuar la secuencia más allá de 1.0011000 y esperar que surja un patrón: Los valores parecen acercarse\(e = 2.718281828...\), la base de los logaritmos naturales. Por lo tanto, tomar el logaritmo de toda la aproximación.
\[ln(1 + z)n = n ln(1 + z). \label{5.30} \]
El razonamiento pictórico mostró que\(ln(1 + z) ≈ z\) cuando\(z ≪ 1\) (Sección 4.3). Así,\(n ln(1 + z) ≈ nz\), haciendo\((1 + z) ≈ e\). Esta aproximación mejorada explica por qué la aproximación\((1 + z)n ≈ 1 + nz\) falló con grande\(nz\): Solo cuando\(nz ≪ 1\) es\(enz\) aproximadamente\(1 + nz\). Por lo tanto, cuando\(z ≪ 1\) las dos aproximaciones más simples son
\ [(1+z) ^ {n}\ aprox\ izquierda\ {\ comenzar {matriz} {ll}
1+n z & (z\ ll 1\ texto {y} n z\ ll 1)\\
e^ {n z} & (z\ ll 1\ texto {y} n z\ texto {no restringido)}
\ end {array}\ derecho. \ label {5.31}\]
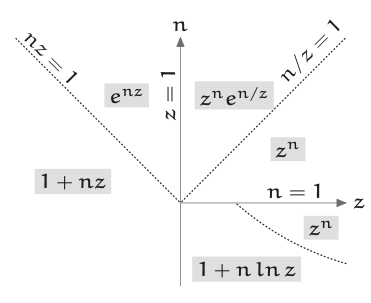
El diagrama muestra, en todo el\(n – z\) plano, la aproximación más simple en cada región. Los ejes son logarítmicos y n y z se suponen positivos: El plano medio derecho se muestra\(z ≫ 1\), y el plano de la mitad superior muestra\(n ≫ 1\). En la parte inferior derecha, la curva límite es\(n ln z = 1\). Explicar los límites y extender las aproximaciones es un ejercicio instructivo (Problema 5.28).
Problema 5.28 Explicando el plano de aproximación
En el plano medio derecho, explique los\(n ln z = 1\) límites\(n/z = 1\) y. Para todo el plano, relajar la suposición de positivo\(n\) y en la\(z\) medida de lo posible.
Problema 5.29 Derivación binomial-teorema
Pruebe la siguiente derivación alternativa de\((1+z)^{n} ≈ e^{nz}\) (dónde\(n ≫ 1\)). Expandir\((1 + z)^{n}\) usando el teorema binomial, simplificar los productos en los coeficientes binomiales aproximando\(n − k\) as\(n\), y comparar la expansión resultante con la serie Taylor para\(e^{nz}\).


