5.4: Aproximación sucesiva - ¿Qué tan profundo es el pozo?
- Page ID
- 112529
La siguiente ilustración de sacar la gran parte enfatiza la aproximación sucesiva y se disfraza como un problema de física.
Se deja caer una piedra por un pozo de profundidad desconocida h y se escucha el chapoteo 4 s después. Descuidando la resistencia al aire, encuentra h a dentro del 5%. Utilízalo\(cs = 340 ms^{−1}\) como la velocidad del sonido y\(g = 10 ms^{−2}\) como la fuerza de la gravedad.
Las soluciones aproximadas y exactas dan casi la misma profundidad de pozo, pero ofrecen entendimientos significativamente diferentes.
Profundidad exacta
La profundidad viene determinada por la restricción de que la espera de 4 s se divide en dos veces: la roca que cae libremente por el pozo y el sonido que sube por el pozo. El tiempo de caída libre es\(\sqrt{2h/g}\) (Problema 1.3), por lo que el tiempo total es
\[T = \underbrace{\sqrt{\frac{2h}{g}}}_{\text{rock}} +\underbrace{\frac{h}{C_{s}}}_{\text{sound}}. \label{5.32} \]
Para resolver\(h\) exactamente, aislar la raíz cuadrada en un lado y cuadrar ambos lados para obtener una ecuación cuadrática en\(h\) (Problema 5.30); o, para un método menos propenso a errores, reescribir la restricción como una ecuación cuadrática en una nueva variable\(z = \sqrt{h}\)
Resuelve\(h\) aislando la raíz cuadrada en un lado y cuadrando ambos lados. ¿Cuáles son las ventajas y desventajas de este método en comparación con el método de reescribir la restricción como cuadrática en\(z = h\)?
Como una ecuación cuadrática en\(z = \sqrt{h}\), la restricción es
\[\frac{1}{c_{s}}Z^{2} + \sqrt{\frac{2}{g}}z - T = 0. \label{5.33} \]
Usando la fórmula cuadrática y eligiendo los rendimientos de raíz positivos
\[Z = \frac{-\sqrt{2/g} + \sqrt{2/g + 4T/c_{s}}}{2/c_{s}}. \label{5.34} \]
Porque\(z^{2} = h\),
\[h = (\frac{-\sqrt{2/g} + \sqrt{2/g + 4T/c_{s}}}{2/c_{s}})^{2}. \label{5.35} \]
Sustituyendo\(g = 10ms^{−2}\) y\(c_{s} = 340ms^{−1}\) da\(h ≈ 71.56m\).
Aunque la profundidad sea correcta, la fórmula exacta para ello es un desastre. Tales horrores de alta entropía surgen frecuentemente de la fórmula cuadrática; su uso a menudo señala el triunfo de la manipulación de símbolos sobre el pensamiento. Las respuestas exactas, encontraremos, pueden ser menos útiles que las respuestas aproximadas.
Profundidad aproximada
Para encontrar una entropía baja, profundidad aproximada, identificar la parte grande, el efecto más importante. Aquí, la mayor parte del tiempo total es la caída libre de la roca: La velocidad máxima de la roca, aunque cayó durante los 4 s enteros, es solo\(gT = 40 ms^{−1}\), que está muy por debajo\(c_{s}\). Por lo tanto, el efecto más importante debería surgir en el caso extremo de la velocidad sonora infinita.
Si\(c_{s} = \infty\), ¿qué tan profundo es el pozo?
En esta aproximación cero, el tiempo de caída libre\(t_{0}\) es el tiempo completo\(T = 4s\), por lo que la profundidad del pozo\(h_{0}\) se vuelve
\[h_{0} = \frac{1}{2}gt^{2}_{0} = 80m. \label{5.36} \]
¿Es esta profundidad aproximada una sobreestimación o subestimación? ¿Qué tan precisa es?
Esta aproximación descuida el tiempo de viaje sonoro, por lo que sobreestima el tiempo de caída libre y por lo tanto la profundidad. En comparación con la profundidad real de aproximadamente 71.56 m, sobreestima la profundidad solo en un 11% de precisión razonable para un método rápido que ofrece una visión física. Además, esta aproximación sugiere su propio refinamiento.
¿Cómo se puede mejorar esta aproximación?
Para mejorarlo, utilice la profundidad aproximada\(h_{0}\) para aproximar el tiempo de viaje del sonido.
\[t_{\text{sound}} ≈ \frac{h_{0}}{c_{s}} ≈ 0.24s. \label{5.37} \]
El tiempo restante es la siguiente aproximación al tiempo de caída libre.
\[t_{1} = T - \frac{h_{0}}{c_{s}} ≈ 3.76s. \label{5.38} \]
En ese tiempo, la roca cae una distancia\(gt^{2}_{1}/2\), por lo que la siguiente aproximación a la profundidad es
\[h_{1} = \frac{1}{2}gt^{2}_{1} ≈ 70.87 m. \label{5.39} \]
¿Es esta profundidad aproximada una sobreestimación o subestimación? ¿Qué tan precisa es?
El cálculo de los\(h_{1}\) utilizados\(h_{0}\) para estimar el tiempo de viaje sonoro. Debido a que h0 sobreestima la profundidad, el procedimiento sobreestima el tiempo de viaje del sonido y, en la misma cantidad, subestima el tiempo de caída libre. Así\(h_{1}\) subestima la profundidad. En efecto,\(h_{1}\) es ligeramente menor que la verdadera profundidad de aproximadamente 71.56 m pero solo 1.3%.
El método de aproximación sucesiva tiene varias ventajas sobre resolver exactamente la fórmula cuadrática. Primero, nos ayuda a desarrollar una comprensión física del sistema; nos damos cuenta, por ejemplo, que la mayor parte del\(T = 4s\) se gasta en caída libre, por lo que la profundidad es más o menos\(gT^{2}/2\). Segundo, tiene una explicación pictórica (Problema 5.34). Tercero, da una respuesta suficientemente precisa rápidamente. Si quieres saber si es seguro saltar al pozo, ¿por qué calcular la profundidad a tres decimales?
Finalmente, el método puede manejar pequeños cambios en el modelo. Tal vez la velocidad del sonido varía con la profundidad, o la resistencia al aire se vuelve importante (Problema 5.32). Entonces falla el método de fuerza bruta, fórmula cuadrática. La fórmula cuadrática y las fórmulas cúbicas y cuárticas aún más desordenados son soluciones raras de forma cerrada a ecuaciones complicadas. La mayoría de las ecuaciones no tienen una solución de forma cerrada. Por lo tanto, un pequeño cambio a un modelo resoluble generalmente produce un modelo intratable si exigimos una respuesta exacta. El método de aproximación sucesiva es una alternativa robusta que produce soluciones comprensibles y de baja entropía.
Problema 5.31 Imprecisiones del valor del parámetro
¿Qué es\(h_{2}\), la segunda aproximación a la profundidad? Compare el error en\(h_{1}\) y\(h_{2}\) con el error realizado al usar\(g = 10ms^{-2}\).
Problema 5.32 Efecto de la resistencia al aire
Más o menos, ¿qué error fraccional en la profundidad se produce al descuidar la resistencia del aire (Sección 2.4.2)? Compare este error con el error en la primera aproximación\(h_{1}\) y en la segunda aproximación\(h_{2}\) (Problema 5.31).
Problema 5.33 Forma adimensional del análisis de profundidad del pozo
Incluso los resultados más desordenados son más limpios y tienen menor entropía en forma adimensional. Las cuatro cantidades\(h, g, T\), y\(c_{s}\) producen dos grupos adimensionales independientes (Sección 2.4.1). Un par intuitivamente razonable son
\[\bar{h} ≡ \frac{h}{gT^{2}} \text{ and } \bar{T} ≡ \frac{gT}{c_{s}}. \label{5.40} \]
a. ¿Qué es una interpretación física\(\bar{T}\)?
b. Con dos grupos, la forma general adimensional es\(\bar{h}\) = f (\(\bar{T}\)). ¿Qué hay\(\bar{h}\) en el caso fácil\(\bar{T}\) → 0?
c. Reescribir la solución de fórmula cuadrática
\[h = (\frac{-\sqrt{2/g} + \sqrt{2/g + 4T/c_{s}}}{2/c_{s}})^{2}. \label{5.41} \]
as\(\bar{h} = f(\bar{T}\)). Entonces comprueba que\(f(\bar{T}\)) se comporta correctamente en el caso fácil\(\bar{T} \rightarrow 0\).
Problema 5.34 Diagrama espacio-tiempo de la profundidad del pozo
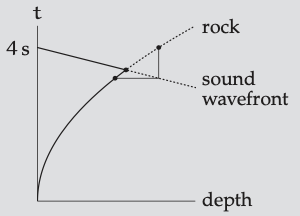
¿Cómo ilustra el diagrama espacio-tiempo [44] la aproximación sucesiva de la profundidad del pozo? En el diagrama, marca\(h_{0}\) (la aproximación cero a la profundidad),\(h_{1}\), y la profundidad exacta h. marca\(t_{0}\), la aproximación cero al tiempo de caída libre. ¿Por qué partes de la roca y las curvas del frente de onda sonora están punteadas? ¿Cómo volverías a dibujar el diagrama si la velocidad del sonido se duplicara? Si g se duplicó?


