2.1: Usar el lenguaje del álgebra (Parte 1)
- Page ID
- 114248
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Usar variables y símbolos algebraicos
- Identificar expresiones y ecuaciones
- Simplifica expresiones con exponentes
- Simplificar las expresiones usando el orden de las operaciones
¡
Antes de comenzar, toma este cuestionario de preparación.
- Agregar:\(43 + 69\). Si te perdiste este problema, revisa el Ejemplo 1.2.8.
- Multiplicar:\((896)201\). Si te perdiste este problema, revisa el Ejemplo 1.4.11.
- Dividir:\(7,263 ÷ 9\). Si te perdiste este problema, revisa el Ejemplo 1.5.8.
Usar variables y símbolos algebraicos
Greg y Alex tienen el mismo cumpleaños, pero nacieron en diferentes años. Este año Greg tiene\(20\) años y Alex es\(23\), así que Alex es\(3\) años mayor que Greg. Cuando Greg estaba\(12\), Alex lo estaba\(15\). Cuando Greg lo esté\(35\), Alex lo estará\(38\). No importa cuál sea la edad de Greg, la edad de Alex siempre será\(3\) años más, ¿verdad?
En el lenguaje del álgebra, decimos que la edad de Greg y la edad de Alex son variables y las tres son una constante. Las edades cambian, o varían, por lo que la edad es una variable. Los\(3\) años entre ellos siempre se mantienen iguales, por lo que la diferencia de edad es la constante.
En álgebra se utilizan letras del alfabeto para representar variables. Supongamos que llamamos a la edad de Greg\(g\). Entonces podríamos usar\(g + 3\) para representar la edad de Alex. Ver Tabla\(\PageIndex{1}\).
| La edad de Greg | La edad de Alex |
|---|---|
| 12 | 15 |
| 20 | 23 |
| 35 | 38 |
| g | g + 3 |
Las letras se utilizan para representar variables. Las letras que a menudo se utilizan para las variables son\(x, y, a, b,\) y\(c\).
Una variable es una letra que representa un número o cantidad cuyo valor puede cambiar.
Una constante es un número cuyo valor siempre permanece igual.
Para escribir algebraicamente, necesitamos algunos símbolos así como números y variables. Hay varios tipos de símbolos que vamos a utilizar. En Números enteros, introdujimos los símbolos para las cuatro operaciones aritméticas básicas: suma, resta, multiplicación y división. Los resumiremos aquí, junto con palabras que usamos para las operaciones y el resultado.
| Operación | Notación | Decir: | El resultado es... |
|---|---|---|---|
| Adición | a + b | a más b | la suma de a y b |
| Resta | a − b | a menos b | la diferencia de a y b |
| Multiplicación | a • b, (a) (b), (a) b, a (b) | a veces b | el producto de a y b |
| División | a ÷ b, a/b\(\dfrac{a}{b}\),\(b \overline{)a}\) | a dividido por b | el cociente de a y b |
En álgebra, el símbolo de la cruz\(×\),, no se utiliza para mostrar la multiplicación porque ese símbolo puede causar confusión. ¿\(3xy\)Significa\(3 × y\) (tres veces\(y\)) o\(3 • x • y\) (tres\(x\) veces\(y\))? Para que quede claro, use\(•\) o paréntesis para multiplicar.
Realizamos estas operaciones en dos números. Al traducir de la forma simbólica a las palabras, o de las palabras a la forma simbólica, preste atención a las palabras de o y para ayudarle a encontrar los números.
La suma de\(5\) y las\(3\) medias agregan\(5\) más\(3\), que escribimos como\(5 + 3\).
La diferencia de\(9\) y las\(2\) medias restan\(9\) menos\(2\), que escribimos como\(9 − 2\).
El producto de\(4\) y\(8\) significa multiplicar\(4\) tiempos\(8\), que podemos escribir como\(4 • 8\).
El cociente de\(20\) y\(5\) los medios dividen\(20\) por\(5\), que podemos escribir como\(20 ÷ 5\).
Traducir de álgebra a palabras:
- \(12 + 14\)
- \((30)(5)\)
- \(64 ÷ 8\)
- \(x − y\)
Solución
| 12 + 14 |
| 12 más 14 |
| la suma de doce y catorce |
| (30) (5) |
| 30 veces 5 |
| el producto de treinta y cinco |
| 64 ÷ 8 |
| 64 dividido por 8 |
| el cociente de sesenta y cuatro y ocho |
| x − y |
| x menos y |
| la diferencia de x e y |
Traducir del álgebra a las palabras.
- \(18 + 11\)
- \((27)(9)\)
- \(84 ÷ 7\)
- \(p − q\)
- Responder a
-
\(18\)más\(11\); la suma de dieciocho y once
- Respuesta b
-
\(27\)veces\(9\); el producto de veintisiete y nueve
- Respuesta c
-
\(84\)dividido por\(7\); el cociente de ochenta y cuatro y siete
- Respuesta d
-
\(p\)menos\(q\); la diferencia de\(p\) y\(q\)
Traducir del álgebra a las palabras.
- \(47 − 19\)
- \(72 ÷ 9\)
- \(m + n\)
- \((13)(7)\)
- Responder a
-
\(47\)menos\(19\); la diferencia de cuarenta y siete y diecinueve
- Respuesta b
-
\(72\)dividido por\(9\); el cociente de setenta y dos y nueve
- Respuesta c
-
\(m\)más\(n\); la suma de\(m\) y\(n\)
- Respuesta d
-
\(13\)veces\(7\); el producto de trece y siete
Cuando dos cantidades tienen el mismo valor, decimos que son iguales y las conectamos con un signo igual.
\(a = b\)se lee\(a\) es igual a\(b\)
El símbolo\(=\) se llama el signo igual.
Una desigualdad se utiliza en álgebra para comparar dos cantidades que pueden tener valores diferentes. La línea numérica puede ayudarte a entender las desigualdades. Recuerda que en la recta numérica los números se hacen más grandes a medida que van de izquierda a derecha. Entonces, si sabemos que\(b\) es mayor que\(a\), significa que\(b\) está a la derecha de\(a\) en la recta numérica. Usamos los símbolos "" y\(<\) "\(>\)"” para las desigualdades.
\(a < b\)se lee\(a\) es menor que\(b\)
\(a\)está a la izquierda de\(b\) en la línea numérica
\(a > b\)se lee\(a\) es mayor que\(b\)
\(a\)está a la derecha de\(b\) en la línea numérica
Las expresiones\(a < b\) y se\(a > b\) pueden leer de izquierda a derecha o de derecha a izquierda, aunque en inglés solemos leer de izquierda a derecha. En general,\(a < b\) es equivalente a\(b > a\). Por ejemplo,\(7 < 11\) es equivalente a\(11 > 7\). \(a > b\)es equivalente a\(b < a\). Por ejemplo,\(17 > 4\) es equivalente a\(4 < 17\).
Cuando escribimos un símbolo de desigualdad con una línea debajo de él, como\(a ≤ b\), significa\(a < b\) o\(a = b\). Leemos que esto\(a\) es menor o igual a\(b\). También, si ponemos una baraja a través de un signo igual\(≠\),, significa no igual.
Resumimos los símbolos de igualdad y desigualdad en la Tabla\(\PageIndex{3}\).
| Notación algebraica | Decir |
|---|---|
| a = b | a es igual a b |
| a ≠ b | a no es igual a b |
| a < b | a es menor que b |
| a > b | a es mayor que b |
| a ≤ b | a es menor o igual que b |
| a ≥ b | a es mayor o igual que b |
Los símbolos\(<\) y\(>\) cada uno tienen un lado más pequeño y un lado más grande.
lado más pequeño lado\(<\) más grande
lado más grande lado\(>\) más pequeño
El lado más pequeño del símbolo está orientado hacia el número más pequeño y cuanto más grande está orientado hacia el número mayor.
Traducir de álgebra a palabras:
- \(20 ≤ 35\)
- \(11 ≠ 15 − 3\)
- \(9 > 10 ÷ 2\)
- \(x + 2 < 10\)
Solución
| 20 ≤ 35 |
| 20 es menor o igual a 35 |
| 11 ≠ 15 − 3 |
| 11 no es igual a 15 menos 3 |
| 9 > 10 ÷ 2 |
| 9 es mayor que 10 dividido por 2 |
| x + 2 < 10 |
| x más 2 es menor que 10 |
Traducir del álgebra a las palabras.
- \(14 ≤ 27\)
- \(19 − 2 ≠ 8\)
- \(12 > 4 ÷ 2\)
- \(x − 7 < 1\)
- Responder a
-
catorce es menor o igual a veintisiete
- Respuesta b
-
diecinueve menos dos no es igual a ocho
- Respuesta c
-
doce es mayor que cuatro dividido por dos
- Respuesta d
-
\(x\)menos siete es menos de uno
Traducir del álgebra a las palabras.
- \(19 ≥ 15\)
- \(7 = 12 − 5\)
- \(15 ÷ 3 < 8\)
- \(y - 3 > 6\)
- Contestar a
-
diecinueve es mayor o igual a quince
- Respuesta b
-
siete es igual a doce menos cinco
- Respuesta c
-
quince dividido por tres es menos de ocho
- Respuesta d
-
\(y\)menos tres es mayor que seis
La información de la Figura\(\PageIndex{1}\) compara el ahorro de combustible en millas-porgalón (mpg) de varios autos. Escribe el símbolo apropiado =, en cada expresión para comparar el ahorro de combustible de los autos.
Figura\(\PageIndex{1}\): (crédito: modificación de obra de Bernard Goldbach, Wikimedia Commons)
- MPG de Prius _____ MPG de Mini Cooper
- MPG de Versa _____ MPG de Ajuste
- MPG de Mini Cooper _____ MPG de Ajuste
- MPG de Corolla _____ MPG de Versa
- MPG de Corolla_____ MPG de Prius
Solución
| MPG de Prius____MPG de Mini Cooper | |
| Encuentra los valores en el gráfico. | 48____27 |
| Comparar. | 48 > 27 |
| MPG de Prius > MPG de Mini Cooper |
| MPG de Versa____MPg de Ajuste | |
| Encuentra los valores en el gráfico. | 26____27 |
| Comparar. | 26 < 27 |
| MPG de Versa < MPG de Ajuste |
| MPG de Mini Cooper____MPG de Ajuste | |
| Encuentra los valores en el gráfico. | 27____27 |
| Comparar. | 27 = 27 |
| MPG de Mini Cooper = MPG de ajuste |
| MPG de Corolla____MPg de Versa | |
| Encuentra los valores en el gráfico. | 28____26 |
| Comparar. | 28 > 26 |
| MPG de Corolla > MPG de Versa |
| MPG de Corolla____MPg de Prius | |
| Encuentra los valores en el gráfico. | 28____48 |
| Comparar. | 28 < 48 |
| MPG de Corolla < MPG de Prius |
Use Figura\(\PageIndex{1}\) para rellenar el símbolo apropiado,\(=\),\(<\), o\(>\).
- MPG de Prius_____MPG de Versa
- MPG de Mini Cooper_____ MPG de Corolla
- Contestar a
-
\(>\)
- Respuesta b
-
\(<\)
Use Figura\(\PageIndex{1}\) para rellenar el símbolo apropiado,\(=\),\(<\), o\(>\).
- MPG de Fit_____ MPG de Prius
- MPG de Corolla _____ MPG de Ajuste
- Contestar a
-
\(<\)
- Respuesta b
-
\(<\)
Agrupar símbolos en álgebra son muy parecidos a las comas, dos puntos y otros signos de puntuación en lenguaje escrito. Indican qué expresiones deben mantenerse juntas y separadas de otras expresiones. Tabla\(\PageIndex{4}\) enumera tres de los símbolos de agrupación más utilizados en álgebra.
| Símbolos de agrupación comunes | |
|---|---|
| paréntesis | () |
| soportes | [] |
| frenillos | {} |
Aquí hay algunos ejemplos de expresiones que incluyen símbolos de agrupación. Simplificaremos expresiones como estas más adelante en esta sección.
\[8(14 - 8) \qquad 21 - 3[2 + 4(9 - 8)] \qquad 24 \div {13 - 2[1(6 - 5) + 4]} \nonumber\]
Identificar expresiones y ecuaciones
¿Cuál es la diferencia en inglés entre una frase y una oración? Una frase expresa un solo pensamiento que está incompleto por sí mismo, pero una oración hace una declaración completa. “Correr muy rápido” es una frase, pero “El futbolista corría muy rápido” es una frase. Una oración tiene un sujeto y un verbo.
En álgebra, tenemos expresiones y ecuaciones. Una expresión es como una frase. Aquí hay algunos ejemplos de expresiones y cómo se relacionan con las frases de palabras:
| Expresión | Palabras | Frase |
|---|---|---|
| 3 + 5 | 3 más 5 | la suma de tres y cinco |
| n - 1 | n menos uno | la diferencia de n y uno |
| 6 • 7 | 6 times 7 | el producto de seis y siete |
| \(\dfrac{x}{y}\) | x dividido por y | el cociente de x e y |
Observe que las frases no forman una oración completa porque la frase no tiene verbo. Una ecuación son dos expresiones vinculadas con un signo igual. Cuando lees las palabras que representan los símbolos en una ecuación, tienes una oración completa en inglés. El signo igual da el verbo. Aquí hay algunos ejemplos de ecuaciones:
| Ecuación | Sentencia |
|---|---|
| 3 + 5 = 8 | La suma de tres y cinco es igual a ocho. |
| n − 1 = 14 | n menos uno es igual a catorce. |
| 6 • 7 = 42 | El producto de seis y siete es igual a cuarenta y dos. |
| x = 53 | x es igual a cincuenta y tres. |
| y + 9 = 2y − 3 | y más nueve es igual a dos y menos tres. |
Una expresión es un número, una variable o una combinación de números y variables y símbolos de operación.
Una ecuación se compone de dos expresiones conectadas por un signo igual.
Determina si cada uno es una expresión o una ecuación:
- \(16 − 6 = 10\)
- \(4 • 2 + 1\)
- \(x ÷ 25\)
- \(y + 8 = 40\)
Solución
| (a) 16 − 6 = 10 | Esta es una ecuación: dos expresiones están conectadas con un signo igual. |
| b) 4 • 2 + 1 | Esta es una expresión, no hay signo igual. |
| (c) x ÷ 25 | Esta es una expresión, no hay signo igual. |
| (d) y + 8 = 40 | Esta es una ecuación: dos expresiones están conectadas con un signo igual. |
Determina si cada uno es una expresión o una ecuación:
- \(23 + 6 = 29\)
- \(7 • 3 − 7\)
- Contestar a
-
ecuación
- Respuesta b
-
expresión
Determina si cada uno es una expresión o una ecuación:
- \(y ÷ 14\)
- \(x − 6 = 21\)
- Contestar a
-
expresión
- Respuesta b
-
ecuación
Simplificar expresiones con exponentes
Simplificar una expresión numérica significa hacer todas las matemáticas posibles. Por ejemplo, para simplificar primero\(4 • 2 + 1\) multiplicaríamos\(4 • 2\) para obtener\(8\) y luego agregaríamos el\(1\) para obtener\(9\). Un buen hábito para desarrollar es trabajar abajo de página, escribiendo cada paso del proceso por debajo del paso anterior. El ejemplo que acabamos de describir se vería así:
\[\begin{split} 4 \cdot 2 + &1 \\ 8 + &1 \\ &9 \end{split}\]
Supongamos que tenemos la expresión\(2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2\). Podríamos escribir esto de manera más compacta usando notación exponencial. La notación exponencial se utiliza en álgebra para representar una cantidad multiplicada por sí misma varias veces. Escribimos\(2 • 2 • 2\) como\(2^3\) y\(2 • 2 • 2 • 2 • 2 • 2 • 2 • 2 • 2\) como\(2^9\). En expresiones como\(2^3\), el\(2\) se llama la base y el\(3\) se llama el exponente. El exponente nos dice cuántos factores de la base tenemos que multiplicar.
significa multiplicar tres factores de\(2\)
Decimos que\(2^3\) está en notación exponencial y\(2 • 2 • 2\) está en notación expandida.
Para cualquier expresión\(a^n\),\(a\) es un factor multiplicado por sí mismo\(n\) veces si\(n\) es un entero positivo.
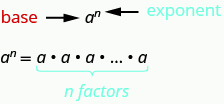
La expresión\(a^n\) se lee\(a\) al\(n^{th}\) poder.
Para poderes de\(n = 2\) y\(n = 3\), tenemos nombres especiales. \(a^2\)se lee como "\(a\)cuadrado”\(a^3\) se lee como "\(a\)cubed” Tabla\(\PageIndex{7}\) enumera algunos ejemplos de expresiones escritas en notación exponencial.
| Notación exponencial | En palabras |
|---|---|
| \(7^2\) | 7 a la segunda potencia, o 7 al cuadrado |
| \(5^3\) | 5 a la tercera potencia, o 5 cubos |
| \(9^4\) | 9 a la cuarta potencia |
| \(12^5\) | 12 a la quinta potencia |
Escribe cada expresión en forma exponencial:
- \(16 • 16 • 16 • 16 • 16 • 16 • 16\)
- \(9 • 9 • 9 • 9 • 9\)
- \(x • x • x • x\)
- \(a • a • a • a • a • a • a • a\)
Solución
| a) La base 16 es un factor 7 veces. | \(16^7\) |
| b) La base 9 es un factor 5 veces. | \(9^5\) |
| (c) La base x es un factor 4 veces. | \(x^4\) |
| d) La base a es un factor 8 veces. | \(a^8\) |
Escribe cada expresión en forma exponencial:\(41 • 41 • 41 • 41 • 41\)
- Responder
-
\(41^5\)
Escribe cada expresión en forma exponencial:\(7 • 7 • 7 • 7 • 7 • 7 • 7 • 7 • 7\)
- Responder
-
\(7^9\)
Escribe cada expresión exponencial en forma expandida:
- \(8^6\)
- \(x^5\)
Solución
- La base es\(8\) y el exponente es\(6\), entonces\(8^6\) significa\(8 • 8 • 8 • 8 • 8 • 8\)
- La base es\(x\) y el exponente es\(5\), entonces\(x^5\) significa\(x • x • x • x • x\)
Escribe cada expresión exponencial en forma expandida:
- \(4^8\)
- \(a^7\)
- Contestar a
-
\(4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\cdot 4\)
- Respuesta b
-
\(a\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a\)
Escribe cada expresión exponencial en forma expandida:
- \(8^8\)
- \(b^6\)
- Contestar a
-
\(8\cdot 8\cdot 8\cdot 8\cdot 8\cdot 8\cdot 8\cdot 8\)
- Respuesta b
-
\(b\cdot b\cdot b\cdot b\cdot b\cdot b\)
Para simplificar una expresión exponencial sin usar una calculadora, la escribimos en forma expandida y luego multiplicamos los factores.
Simplificar:\(3^4\).
Solución
| Expandir la expresión. | 3 4 = 3 • 3 • 3 • 3 |
| Multiplicar de izquierda a derecha. | 9 • 3 • 3 = 27 • 3 |
| Multiplicar. | 81 |
Simplificar:
- \(5^3\)
- \(1^7\)
- Contestar a
-
\(125\)
- Respuesta b
-
\(1\)
Simplificar:
- \(7^2\)
- \(0^5\)
- Contestar a
-
\(49\)
- Respuesta b
-
\(0\)