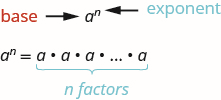2.2: Usar el lenguaje del álgebra (Parte 2)
- Page ID
- 114260
Simplificar las expresiones usando el orden de las operaciones
Hemos introducido la mayoría de los símbolos y notación utilizados en álgebra, pero ahora necesitamos aclarar el orden de las operaciones. De lo contrario, las expresiones pueden tener diferentes significados, y pueden dar como resultado valores diferentes. Por ejemplo, considere la expresión:\[4 + 3 \cdot 7 \nonumber\]
| Algunos estudiantes dicen que simplifica | 49 | Algunos estudiantes dicen que simplifica | 25 |
| Desde 4 + 3 da 7. | 4 + 3 • 7 = 7 • 7 | Desde 3 • 7 es 21. | 4 + 3 • 7 = 4 + 21 |
| Y 7 • 7 es 49. | 7 • 7 = 49 | Y 21 + 4 hace 25. | 4 + 21 = 25 |
Imagínese la confusión que podría resultar si cada problema tuviera varias respuestas correctas diferentes. La misma expresión debería dar el mismo resultado. Por lo que los matemáticos establecieron algunas pautas llamadas el orden de las operaciones, que esboza el orden en que deben simplificarse las partes de una expresión.
Al simplificar las expresiones matemáticas, realice las operaciones en el siguiente orden:
- P arentesis y otros símbolos de agrupación
- Simplifica todas las expresiones dentro de los paréntesis u otros símbolos de agrupación, trabajando primero en los paréntesis más internos.
- E xponentes
- Simplifica todas las expresiones con exponentes.
- M ultiplicación y D ivision
- Realiza toda la multiplicación y división en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
- Una ddición y sustracción S
- Realizar todas las sumas y restas en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
Los estudiantes a menudo preguntan: “¿Cómo voy a recordar el orden?” Aquí hay una manera de ayudarte a recordar: Toma la primera letra de cada palabra clave y sustituye la frase tonta. P arrendamiento E xcuse M y D oreja A unt S aliado.
| Orden de Operaciones | |
|---|---|
| P arrendamiento | P arentesis |
| E xcuse | E xponentes |
| Oreja M y D | M ultiplicación y D ivision |
| Un aliado unt S | Una ddición y sustracción S |
Es bueno que 'M y D oreja' vaya de la mano, ya que esto nos recuerda que m ultiplicación y d ivisión tienen igual prioridad. No siempre hacemos multiplicación antes de la división o siempre hacemos división antes de multiplicar. Los hacemos en orden de izquierda a derecha.
De igual manera, 'A unt S ally' va de la mano y así nos recuerda que una ddition y una s ubtracción también tienen igual prioridad y las hacemos en orden de izquierda a derecha.
Simplifica las expresiones:
- \(4 + 3 • 7\)
- \((4 + 3) • 7\)
Solución
| ¿Hay paréntesis? No. ¿Hay exponentes? No. ¿Hay alguna multiplicación o división? Sí. | \(4 + 3 \cdot 7\) |
| Multiplicar primero. | \(4 + \textcolor{red}{3 \cdot 7}\) |
| Agregar. | \(4 + 21\) |
| \(25\) |
| ¿Hay paréntesis? Sí. | \((4 + 3) \cdot 7\) |
| Simplifica dentro de los paréntesis. | \(\textcolor{red}{(4 + 3)} \cdot 7\) |
| ¿Hay exponentes? No. ¿Hay alguna multiplicación o división? Sí. | \((7)7\) |
| Multiplicar. | \(49\) |
Simplifica las expresiones:
- \(12 − 5 • 2\)
- \((12 − 5) • 2\)
- Contestar a
-
\(2\)
- Respuesta b
-
\(14\)
Simplifica las expresiones:
- \(8 + 3 • 9\)
- \((8 + 3) • 9\)
- Contestar a
-
\(35\)
- Respuesta b
-
\(99\)
Simplificar:
- \(18 ÷ 9 • 2\)
- \(18 • 9 ÷ 2\)
Solución
| ¿Hay paréntesis? No. ¿Hay exponentes? No. ¿Hay alguna multiplicación o división? Sí. | \(18 \div 9 \cdot 2\) |
| Multiplicar y dividir de izquierda a derecha. Dividir. | \(\textcolor{red}{2} \cdot 2\) |
| Multiplicar. | \(4\) |
| ¿Hay paréntesis? No. ¿Hay exponentes? No. ¿Hay alguna multiplicación o división? Sí. | \(18 \cdot 9 \div 2\) |
| Multiplicar y dividir de izquierda a derecha. Multiplicar. | \(\textcolor{red}{162} \div 2\) |
| Dividir. | \(81\) |
Simplificar:\(42 ÷ 7 • 3\)
- Responder
-
\(18\)
Simplificar:\(12 • 3 ÷ 4\)
- Responder
-
\(9\)
Simplificar:\(18 ÷ 6 + 4(5 − 2)\).
Solución
| ¿Paréntesis? Sí, restar primero. | \(18 \div 6 + 4(5-2)\) |
| ¿Exponentes? No. ¿Multiplicación o división? Sí. | \(18 \div 6 + 4(\textcolor{red}{3})\) |
| Dividir primero porque multiplicamos y dividimos de izquierda a derecha. | \(\textcolor{red}{3} + 4(3)\) |
| ¿Alguna otra multiplicación o división? Sí. Multiplicar. | \(3 + \textcolor{red}{12}\) |
| ¿Alguna otra multiplicación o división? No. ¿Alguna suma o resta? Sí | \(15\) |
Simplificar:\(30 ÷ 5 + 10(3 − 2)\)
- Responder
-
\(16\)
Simplificar:\(70 ÷ 10 + 4(6 − 2)\)
- Responder
-
\(23\)
Cuando hay múltiples símbolos de agrupación, simplificamos primero los paréntesis más internos y trabajamos hacia afuera.
Simplificar:\(5 + 2^3 + 3[6 − 3(4 − 2)]\).
Solución
| ¿Hay paréntesis (u otro símbolo de agrupación)? Sí. | \(5 + 2^{3} + 3[6-3(4-2)]\) |
| Enfócate en los paréntesis que están dentro de los corchetes. | \(5 + 2^{3} + 3[6-3 \textcolor{red}{(4-2)}]\) |
| Restar. | \(5 + 2^{3} + 3[6- \textcolor{red}{3(2)}]\) |
| Continuar dentro de los corchetes y multiplicar. | \(5 + 2^{3} + 3[6- \textcolor{red}{6}]\) |
| Continuar dentro de los corchetes y restar. | \(5 + 2^{3} + 3[\textcolor{red}{0}]\) |
| La expresión dentro de los corchetes no requiere más simplificación. | |
| ¿Hay exponentes? Sí. | \(5 + \textcolor{red}{2^{3}} + 3[0]\) |
| Simplifica los exponentes. | \(5 + \textcolor{red}{8} + 3[0]\) |
| ¿Hay alguna multiplicación o división? Sí. | \(5 + 8 + \textcolor{red}{3[0]}\) |
| Multiplicar. | \(5 + 8 + \textcolor{red}{0}\) |
| ¿Hay alguna suma o resta? Sí. | \(textcolor{red}{5+8+0}\) |
| Agregar. | \(\textcolor{red}{13} + 0\) |
| Agregar. | \(13\) |
Simplificar:\(9 + 5^3 − [4(9 + 3)]\)
- Responder
-
\(86\)
Simplificar:\(7^2 − 2[4(5 + 1)]\)
- Responder
-
\(1\)
Simplificar:\(2^3 + 34 ÷ 3 − 5^2\).
Solución
| Si una expresión tiene varios exponentes, pueden simplificarse en un mismo paso. | \(2^{3} + 3^{4} \div 3 - 5{2}\) |
| Simplifica los exponentes. | \(\textcolor{red}{2^{3}} + \textcolor{red}{3^{4}} \div 3 - \textcolor{red}{5^{2}}\) |
| Dividir. | \(8 + \textcolor{red}{81 \div 3} - 25\) |
| Agregar. | \(\textcolor{red}{8+27} - 25\) |
| Restar. | \(\textcolor{red}{35-25}\) |
| \(10\) |
Simplificar:\(3^2 + 2^4 ÷ 2 + 4^3\)
- Responder
-
\(81\)
Simplificar:\(6^2 − 5^3 ÷ 5 + 8^2\)
- Responder
-
\(75\)
Acceda a recursos adicionales en línea
Conceptos clave
| Operación | Notación | Decir: | El resultado es... |
|---|---|---|---|
| Adición | la suma de | ||
| Multiplicación | El producto de | ||
| Resta | la diferencia de | ||
| División | \(a\div b, a/b, \dfrac{a}{b}, a \overline{\smash{)}b}\) | El cociente de |
- Símbolo de igualdad
- El símbolo\(=\) se llama el signo igual.
- Desigualdad
- \(a>b\)se lee\(a\) es mayor que\(b\)
| Notación algebraica | Decir |
|---|---|
| es menor o igual a | |
| es mayor o igual a |
- Notación exponencial
- Para cualquier expresión\(a^n\) es un factor multiplicado por sí mismo
- La expresión de
Orden de Operaciones Al simplificar las expresiones matemáticas, realice las operaciones en el siguiente orden:
- Paréntesis y otros símbolos de agrupación: Simplifique todas las expresiones dentro de los paréntesis u otros símbolos de agrupación, trabajando primero en los paréntesis más internos.
- Exponentes: Simplifica todas las expresiones con exponentes.
- Multiplicación y División: Realiza todas las multiplicaciones y divisiones en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
- Suma y resta: Realiza todas las sumas y restas en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
Glosario
- expresiones
-
Una expresión es un número, una variable o una combinación de números y variables y símbolos de operación.
- ecuación
-
Una ecuación se compone de dos expresiones conectadas por un signo igual.
La práctica hace la perfección
Usar variables y símbolos algebraicos
En los siguientes ejercicios, traduzca de la notación algebraica a las palabras.
- 16 − 9
- 25 − 7
- 5 • 6
- 3 • 9
- 28 ÷ 4
- 45 ÷ 5
- x + 8
- x + 11
- (2) (7)
- (4) (8)
- 14 < 21
- 17 < 35
- 36 ≥ 19
- 42 ≥ 27
- 3n = 24
- 6n = 36
- y − 1 > 6
- y − 4 > 8
- 2 ≤ 18 ÷ 6
- 3 ≤ 20 ÷ 4
- a ≠ 7 • 4
- a ≠ 1 • 12
Identificar expresiones y ecuaciones
En los siguientes ejercicios, determine si cada uno es una expresión o una ecuación.
- 9 • 6 = 54
- 7 • 9 = 63
- 5 • 4 + 3
- 6 • 3 + 5
- x + 7
- x + 9
- y − 5 = 25
- y − 8 = 32
Simplificar expresiones con exponentes
En los siguientes ejercicios, escribe en forma exponencial.
- 3 • 3 • 3 • 3 • 3 • 3 • 3
- 4 • 4 • 4 • 4 • 4 • 4
- x • x • x • x
- y • y • y • y • y
En los siguientes ejercicios, escribe en forma expandida.
- 5 3
- 8 3
- 2 8
- 10 5
Simplificar las expresiones usando el orden de las operaciones
En los siguientes ejercicios, simplifique.
- (a) 3 + 8 • 5 (b) (3+8) • 5
- (a) 2 + 6 • 3 (b) (2+6) • 3
- 2 3 − 12 ÷ (9 − 5)
- 3 2 − 18 ÷ (11 − 5)
- 3 • 8 + 5 • 2
- 4 • 7 + 3 • 5
- 2 + 8 (6 + 1)
- 4 + 6 (3 + 6)
- 4 • 12/8
- 2 • 36/6
- 6 + 10/2 + 2
- 9 + 12/3 + 4
- (6 + 10) ÷ (2 + 2)
- (9 + 12) ÷ (3 + 4)
- 20 ÷ 4 + 6 • 5
- 33 ÷ 3 + 8 • 2
- 20 ÷ (4 + 6) • 5
- 33 ÷ (3 + 8) • 2
- 4 2 + 5 2
- 3 2 + 7 2
- (4 + 5) 2
- (3 + 7) 2
- 3 (1 + 9 • 6) − 4 2
- 5 (2 + 8 • 4) − 7 2
- 2 [1 + 3 (10 − 2)]
- 5 [2 + 4 (3 − 2)]
Matemáticas cotidianas
- Basquetbol En los playoffs de la NBA 2014, los San Antonio Spurs vencieron al Miami Heat. En la siguiente tabla se muestran las alturas de los abridores en cada equipo. Utilice esta tabla para rellenar el símbolo apropiado (=, <, >).
| Espuelas | Altura | Calor | Altura |
|---|---|---|---|
| Tim Duncan | 83″ | Rashard Lewis | 82" |
| Boris Diaw | 80" | LeBron James | 80" |
| Kawhi Leonard | 79" | Chris Bosh | 83" |
| Tony Parker | 74" | Dwyane Wade | 76" |
| Danny Green | 78" | Ray Allen | 77" |
- Altura de Tim Duncan____Altura de Rashard Lewis
- Altura de Boris Diaw____Altura de LeBron James
- Altura de Kawhi Leonard____Altura de Chris Bosh
- Altura de Tony Parker____Altura de Dwyane Wade
- Altura de Danny Green____Altura de Ray Allen
- Elevación En Colorado hay más de 50 montañas con una elevación de más de 14,000 pies. En la tabla se muestran los diez más altos. Utilice esta tabla para rellenar el símbolo de desigualdad apropiado.
| Montaña | Elevación |
|---|---|
| Mt. Elbert | 14,433′ |
| Mt. Masiva | 14,421′ |
| Mt. Harvard | 14,420′ |
| Pico Blanca | 14,345′ |
| Pico La Plata | 14,336′ |
| Pico Uncompahgre | 14,309′ |
| Pico Crestón | 14,294′ |
| Mt. Lincoln | 14,286′ |
| Pico Grays | 14,270′ |
| Mt. Antero | 14,269′ |
- Elevación de La Plata Pico____Elevación del Monte. Antero
- Elevación del pico Blanca____Elevación del monte. Elbert
- Elevación del pico de Gray ____Elevación del monte. Lincoln
- Elevación del monte. Masiva____Elevación del Pico Crestone
- Elevación del monte. Cosecha____Elevación del Pico Uncompahgre
Ejercicios de escritura
- Explicar la diferencia entre una expresión y una ecuación.
- ¿Por qué es importante utilizar el orden de las operaciones para simplificar una expresión?
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
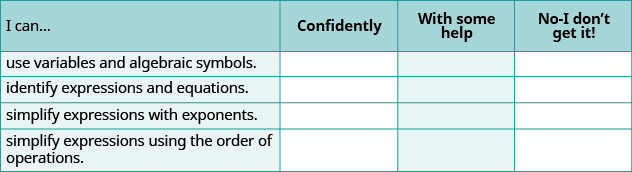
(b) Si la mayoría de sus cheques fueron:
... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.
... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas, cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?
... no, ¡no lo comprendo! Esta es una señal de advertencia y no debes ignorarla. Debería obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.