2.5: Resolver ecuaciones usando las propiedades de resta y suma de la igualdad (Parte 1)
- Page ID
- 114255
- Determinar si un número es una solución de una ecuación
- Modelar la Propiedad de Sustracción de Igualdad
- Resolver ecuaciones usando la Propiedad de Sustracción de Igualdad
- Resolver ecuaciones usando la Propiedad de Suma de Igualdad
- Traducir frases de palabras a ecuaciones algebraicas
- Traducir a una ecuación y resolver
¡
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar\(x + 8\) cuándo\(x = 11\). Si te perdiste este problema, revisa el Ejemplo 2.. 2.1.
- Evaluar\(5x − 3\) cuándo\(x = 9\). Si te perdiste este problema, revisa el Ejemplo 2.2.2.
- Traducir al álgebra: la diferencia de\(x\) y\(8\). Si te perdiste este problema, revisa el Ejemplo 2.2.11.
Cuando algunas personas escuchan la palabra álgebra, piensan en resolver ecuaciones. Las aplicaciones de la resolución de ecuaciones son ilimitadas y se extienden a todas las carreras y campos. En esta sección, comenzaremos a resolver ecuaciones. Comenzaremos resolviendo ecuaciones básicas, y luego a medida que avasemos por el curso vamos a construir nuestras habilidades para cubrir muchas formas diferentes de ecuaciones.
Determinar si un número es una solución de una ecuación
Resolver una ecuación es como descubrir la respuesta a un rompecabezas. Una ecuación algebraica establece que dos expresiones algebraicas son iguales. Resolver una ecuación es determinar los valores de la variable que hacen de la ecuación una declaración verdadera. Cualquier número que haga verdadera la ecuación se denomina solución de la ecuación. ¡Es la respuesta al rompecabezas!
Una solución a una ecuación es un valor de una variable que hace una declaración verdadera cuando se sustituye en la ecuación. El proceso de encontrar la solución a una ecuación se llama resolver la ecuación.
Encontrar la solución a una ecuación significa encontrar el valor de la variable que hace verdadera la ecuación. ¿Se puede reconocer la solución de\(x + 2 = 7\)? Si lo dijiste\(5\), ¡tienes razón! Decimos que\(5\) es una solución a la ecuación\(x + 2 = 7\) porque cuando\(5\) sustituimos\(x\) la afirmación resultante es verdad.
\[\begin{split} x + 2 & = 7 \\ 5 + 2 & \stackrel{?}{=} 7 \\ 7 & = 7 \; \checkmark \end{split} \nonumber \]
Ya que\(5 + 2 = 7\) es una afirmación verdadera, sabemos que efectivamente\(5\) es una solución a la ecuación. El símbolo\(\stackrel{?}{=}\) pregunta si el lado izquierdo de la ecuación es igual al lado derecho. Una vez que sabemos, podemos cambiar a un signo igual (\(=\)) o signo no igual (\(≠\)).
Paso 1. Sustituir el número por la variable en la ecuación.
Paso 2. Simplifica las expresiones en ambos lados de la ecuación.
Paso 3. Determinar si la ecuación resultante es verdadera.
- Si es cierto, el número es una solución.
- Si no es cierto, el número no es una solución.
Determinar si\(x = 5\) es una solución de\(6x − 17 = 16\).
Solución
| \(6x − 17 = 16\) | |
| Sustituto\(\textcolor{red}{5}\) por x. | \(6 \cdot \textcolor{red}{5} - 17 \stackrel{?}{=} 16\) |
| Multiplicar. | \(30 - 17 \stackrel{?}{=} 16\) |
| Restar | \(13 \neq 16\) |
Entonces no\(x = 5\) es una solución a la ecuación\(6x − 17 = 16\).
¿Es\(x = 3\) una solución de\(4x − 7 = 16\)?
- Contestar
-
no
¿Es\(x = 2\) una solución de\(6x − 2 = 10\)?
- Contestar
-
si
Determinar si\(y = 2\) es una solución de\(6y − 4 = 5y − 2\).
Solución
Aquí, la variable aparece en ambos lados de la ecuación. Debemos sustituir a\(2\) cada uno\(y\).
| \(6y − 4 = 5y − 2\) | |
| Sustituto\(\textcolor{red}{2}\) de y. | \(6(\textcolor{red}{2}) - 4 \stackrel{?}{=} 5(\textcolor{red}{2}) - 2\) |
| Multiplicar. | \(12 - 4 \stackrel{?}{=} 10 - 2\) |
| Restar | \(8 = 8 \; \checkmark\) |
Dado que\(y = 2\) resulta en una ecuación verdadera, sabemos que\(2\) es una solución a la ecuación\(6y − 4 = 5y − 2\).
¿Es\(y = 3\) una solución de\(9y − 2 = 8y + 1\)?
- Contestar
-
si
¿Es\(y = 4\) una solución de\(5y − 3 = 3y + 5\)?
- Contestar
-
si
Modelar la Propiedad de Sustracción de Igualdad
Usaremos un modelo para ayudarte a entender cómo el proceso de resolver una ecuación es como resolver un rompecabezas. Un sobre representa la variable —ya que se desconoce su contenido— y cada contador representa uno.
Supongamos que un escritorio tiene una línea imaginaria dividiéndola por la mitad. Colocamos tres mostradores y un sobre en el lado izquierdo del escritorio, y ocho mostradores en el lado derecho del escritorio como en la Figura\(\PageIndex{1}\). Ambos lados del escritorio tienen el mismo número de mostradores, pero algunos mostradores están ocultos en el sobre. ¿Se puede decir cuántos mostradores hay en el sobre?
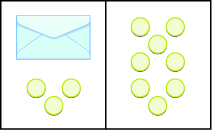
Figura\(\PageIndex{1}\)
¿Qué pasos estás tomando en tu mente para averiguar cuántos contadores hay en el sobre? Quizás estés pensando “Necesito quitar los\(3\) contadores del lado izquierdo para obtener el sobre por sí mismo. Esos\(3\) contadores de la izquierda coinciden con\(3\) los de la derecha, así puedo quitárselos de ambos lados. Eso deja cinco contadores a la derecha, por lo que debe haber\(5\) mostradores en el sobre”. La figura\(\PageIndex{2}\) muestra este proceso.
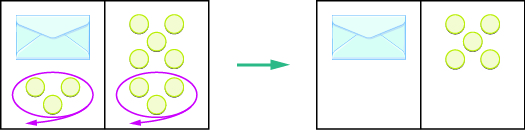
Figura\(\PageIndex{2}\)
¿Qué ecuación algebraica es modelada por esta situación? Cada lado del escritorio representa una expresión y la línea central toma el lugar del signo igual. Llamaremos al contenido del sobre\(x\), por lo que el número de contadores en el lado izquierdo del escritorio es\(x + 3\). En el lado derecho del escritorio hay\(8\) mostradores. Se nos dice que\(x + 3\) es igual a\(8\) así es nuestra ecuación\(x + 3 = 8\).

Figura\(\PageIndex{3}\)
\(x + 3 = 8\)
Escribamos algebraicamente los pasos que dimos para descubrir cuántos contadores había en el sobre.
| \(x + 3 = 8\) | |
| Primero, nos quitamos tres de cada lado. | \(x + 3 \textcolor{red}{-3} = 8 \textcolor{red}{-3}\) |
| Entonces nos quedamos con cinco. | \(x = 5\) |
Ahora vamos a comprobar nuestra solución. Nosotros\(5\) sustituimos\(x\) en la ecuación original y vemos si obtenemos una declaración verdadera.
\[\begin{split} x + 3 & = 8 \\ \textcolor{red}{5} + 3 & \stackrel{?}{=} 8 \\ 8 & = 8 \; \checkmark \end{split} \nonumber \]
Nuestra solución es correcta. Cinco contadores en el sobre más tres más equivale a ocho
Escribe una ecuación modelada por los sobres y contadores, y luego resuelve la ecuación:
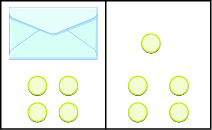
Figura\(\PageIndex{4}\)
Solución
| A la izquierda, escribe x para el contenido del sobre, agrega los 4 contadores, así tenemos x + 4. | x + 4 |
| A la derecha, hay 5 mostradores. | 5 |
| Los dos lados son iguales. | x + 4 = 5 |
| Resuelve la ecuación restando 4 contadores de cada lado. |
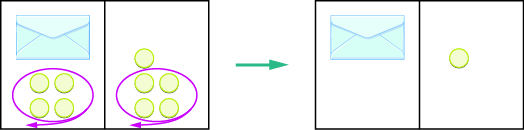
Figura\(\PageIndex{5}\)
Podemos ver que hay un contador en el sobre. Esto se puede mostrar algebraicamente como:
\[\begin{split} x + 4 & = 5 \\ x + 4 \textcolor{red}{-4} & = 5 \textcolor{red}{-4} \\ x & = 1 \end{split} \nonumber \]
Sustituir\(1\)\(x\) en la ecuación a verificar.
\[\begin{split} x + 4 & = 5 \\ \textcolor{red}{1} + 4 & \stackrel{?}{=} 5 \\ 5 & = 5 \; \checkmark \end{split} \nonumber \]
Ya\(x = 1\) que hace que la afirmación sea cierta, sabemos que efectivamente\(1\) es una solución.
Escribe la ecuación modelada por los sobres y contadores, y luego resuelve la ecuación:
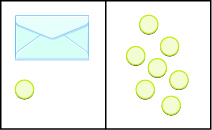
Figura\(\PageIndex{6}\)
- Contestar
-
\(x + 1 = 7; x = 6\)
Escribe la ecuación modelada por los sobres y contadores, y luego resuelve la ecuación:
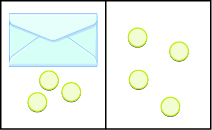
Figura\(\PageIndex{7}\)
- Contestar
-
\(x + 3 = 4; x = 1\)
Resolver ecuaciones usando la propiedad de sustracción de igualdad
Nuestro rompecabezas nos ha dado una idea de lo que debemos hacer para resolver una ecuación. El objetivo es aislar la variable por sí misma en un lado de las ecuaciones. En los ejemplos anteriores, se utilizó la Propiedad de Sustracción de Igualdad, que establece que cuando restamos la misma cantidad de ambos lados de una ecuación, todavía tenemos igualdad.
Para cualquier número\(a\),\(b\), y\(c\), si\(a = b\) entonces\(a − c = b − c\)
Piensa en los hermanos gemelos Andy y Bobby. Tienen\(17\) años. ¿Cuántos años tenía Andy hace\(3\) años? Tenía\(3\) años menos que\(17\), entonces su edad era\(17 − 3\), o\(14\). ¿Qué pasa con la edad de Bobby hace\(3\) años? Por supuesto, él\(14\) también lo fue. Sus edades son iguales ahora, y restar la misma cantidad de ambos resultó en edades iguales\(3\) años atrás.
\[\begin{split} a & = b \\ a - 3 & = b - 3 \end{split} \nonumber \]
Paso 1. Utilice la Propiedad de Sustracción de Igualdad para aislar la variable.
Paso 2. Simplifica las expresiones en ambos lados de la ecuación.
Paso 3. Consulta la solución.
Resolver:\(x + 8 = 17\).
Solución
Utilizaremos la Propiedad de Resta de Igualdad para aislar\(x\).
| \(x + 8 = 17\) | |
| Restar 8 de ambos lados. | \(x + 8 \textcolor{red}{-8} = 17 \textcolor{red}{-8}\) |
| Simplificar. | \(x = 9\) |
| Consulta la solución. | \(\textcolor{red}{9} + 8 = 17\) |
| \(17 = 17 \; \checkmark\) |
Ya\(x = 9\) que hace\(x + 8 = 17\) una verdadera afirmación, sabemos que\(9\) es la solución a la ecuación.
Resolver:\(x + 6 = 19\)
- Contestar
-
\(x=13\)
Resolver:\(x + 9 = 14\)
- Contestar
-
\(x=5\)
Resolver:\(100 = y + 74\).
Solución
Para resolver una ecuación, siempre debemos aislar la variable, no importa de qué lado se encuentre. Para aislar y, restaremos\(74\) de ambos lados.
| \(100 = y + 74\) | |
| Restar 74 de ambos lados. | \(100 \textcolor{red}{-74} = y + 74 \textcolor{red}{-74}\) |
| Simplificar. | \(26 = y\) |
| Sustituye 26 para y para verificar | \(100 \stackrel{?}{=} \textcolor{red}{26} + 74\) |
| \(100 = 100 \; \checkmark\) |
Ya\(y = 26\) que hace\(100 = y + 74\) una verdadera afirmación, hemos encontrado la solución a esta ecuación.
Resolver:\(95 = y + 67\)
- Contestar
-
\(y=28\)
Resolver:\(91 = y + 45\)
- Contestar
-
\(y=46\)
Resolver ecuaciones usando la propiedad de suma de igualdad
En todas las ecuaciones que hemos resuelto hasta el momento, se agregó un número a la variable en un lado de la ecuación. Se utilizó la resta para “deshacer” la suma con el fin de aislar la variable.
Pero supongamos que tenemos una ecuación con un número restado de la variable, tal como\(x − 5 = 8\). Queremos aislar la variable, así que para “deshacer” la resta agregaremos el número a ambos lados.
Utilizamos la Propiedad de Suma de Igualdad, que dice que podemos agregar el mismo número a ambos lados de la ecuación sin cambiar la igualdad. Observe cómo refleja la Propiedad de Resta de Igualdad.
Para cualquier número\(a\),\(b\), y\(c\), si\(a = b\) entonces\(a + c = b + c\)
¿Recuerdas a los gemelos de\(17\) un año, Andy y Bobby? En diez años, la edad de Andy seguirá siendo igual a la de Bobby. Ambos lo serán\(27\).
\[\begin{split} a & = b \\ a + 10 & = b + 10 \end{split} \nonumber \]
Podemos sumar el mismo número a ambos lados y seguir manteniendo la igualdad.
Paso 1. Utilice la Propiedad de Suma de Igualdad para aislar la variable.
Paso 2. Simplifica las expresiones en ambos lados de la ecuación.
Paso 3. Consulta la solución.
Resolver:\(x − 5 = 8\).
Solución
Utilizaremos la Propiedad de Adición de Igualdad para aislar la variable.
| \(x − 5 = 8\) | |
| Agrega 5 a ambos lados. | \(x − 5 \textcolor{red}{+5} = 8 \textcolor{red}{+5}\) |
| Simplificar | \(x = 13\) |
| Ahora ya podemos verificar. Dejar x =\(\textcolor{red}{13}\). | \(\textcolor{red}{13} - 5 \stackrel{?}{=} 8\) |
| \(8 = 8 \; \checkmark\) |
Resolver:\(x − 9 = 13\)
- Contestar
-
\(x=22\)
Resolver:\(y − 1 = 3\)
- Contestar
-
\(y=4\)
Resolver:\(27 = a − 16\).
Solución
Vamos\(16\) a agregar a cada lado para aislar la variable.
| \(27 = a − 16\) | |
| Agrega 16 a cada lado. | \(27 \textcolor{red}{+16} = a − 16 \textcolor{red}{+16}\) |
| Simplificar. | \(43 = a\) |
| Ahora ya podemos verificar. Dejar a =\(\textcolor{red}{43}\). | \(27 \stackrel{?}{=} \textcolor{red}{43} - 16\) |
| \(27 = 27 \; \checkmark\) |
La solución a\(27 = a − 16\) es\(a = 43\).
Resolver:\(19 = a − 18\)
- Contestar
-
\(a=37\)
Resolver:\(27 = n − 14\)
- Contestar
-
\(n=41\)


