2.7: Encontrar múltiplos y factores (Parte 1)
- Page ID
- 114252
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Identificar múltiplos de números
- Usar pruebas comunes de divisibilidad
- Encuentra todos los factores de un número
- Identificar números primos y compuestos
¡
Antes de comenzar, toma este cuestionario de preparación.
- ¿Cuáles de los siguientes números son números de conteo (números naturales)? \(0, 4, 215\)Si te perdiste este problema, revisa el Ejemplo 1.1.1.
- Encuentra la suma de\(3\),\(5\), y\(7\). Si te perdiste el problema, revisa la Sección 2.1.
Identificar múltiplos de números
Annie está contando los zapatos en su clóset. Los zapatos se emparejan en pares, así que no tiene que contar cada uno. Ella cuenta por dos:\(2, 4, 6, 8, 10, 12\). Ella tiene\(12\) zapatos en su clóset.
Los números\(2, 4, 6, 8, 10, 12\) se llaman múltiplos de\(2\). Los múltiplos de se\(2\) pueden escribir como producto de un número de conteo y\(2\). A continuación se dan los\(2\) primeros seis múltiplos de.
\[\begin{split} 1 \cdot 2 & = 2 \\ 2 \cdot 2 & = 4 \\ 3 \cdot 2 & = 6 \\ 4 \cdot 2 & = 8 \\ 5 \cdot 2 & = 10 \\ 6 \cdot 2 &= 12 \end{split} \nonumber \]
Un múltiplo de un número es el producto del número y un número de conteo. Entonces un múltiplo de\(3\) sería producto de un número de conteo y\(3\). A continuación se presentan los primeros seis múltiplos de\(3\).
\[\begin{split} 1 \cdot 3 & = 3 \\ 2 \cdot 3 & = 6 \\ 3 \cdot 3 & = 9 \\ 4 \cdot 3 & = 12 \\ 5 \cdot 3 & = 15 \\ 6 \cdot 3 &= 18 \end{split} \nonumber \]
Podemos encontrar los múltiplos de cualquier número continuando con este proceso. \(\PageIndex{1}\)La tabla muestra los múltiplos de\(2\) through\(9\) para los primeros doce números de conteo.
| Número de conteo | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Multiplos de 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Multiplos de 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| Multiplos de 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| Multiplos de 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Multiplos de 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| Multiplos de 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| Multiplos de 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| Multiplos de 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
Un número es un múltiplo de\(n\) si es producto de un número de conteo y\(n\).
Reconocer los patrones para múltiplos de\(2\)\(5\),\(10\),, y te\(3\) será útil a medida que continúes en este curso.
La figura\(\PageIndex{1}\) muestra los números de conteo de\(1\) a\(50\). \(2\)Se resaltan múltiplos de. ¿Te das cuenta de un patrón?
Figura\(\PageIndex{1}\): Multiplos de 2 entre 1 y 50
El último dígito de cada número resaltado en la Figura\(\PageIndex{1}\) es o bien\(0\)\(2\)\(4\),\(6\),, o\(8\). Esto es cierto para el producto de\(2\) y cualquier número de conteo. Entonces, para saber si algún número es un múltiplo de\(2\) mirar el último dígito. Si es\(0\),,\(2\),\(4\)\(6\), o\(8\), entonces el número es un múltiplo de\(2\).
Determine si cada uno de los siguientes es un múltiplo de\(2\):
- \(489\)
- \(3,714\)
Solución
| ¿489 es múltiplo de 2? | |
| ¿El último dígito es 0, 2, 4, 6 u 8? | No. |
| 489 no es múltiplo de 2. |
| ¿3.714 es múltiplo de 2? | |
| ¿El último dígito es 0, 2, 4, 6 u 8? | Sí. |
| 3,714 es un múltiplo de 2. |
Determine si cada número es un múltiplo de\(2\):
- \(678\)
- \(21,493\)
- Contestar a
-
si
- Respuesta b
-
no
Determine si cada número es un múltiplo de\(2\):
- \(979\)
- \(17,780\)
- Contestar a
-
no
- Respuesta b
-
si
Ahora veamos múltiplos de\(5\). La figura\(\PageIndex{2}\) destaca todos los múltiplos de\(5\) entre\(1\) y\(50\). ¿Qué notas sobre los múltiplos de\(5\)?
Figura\(\PageIndex{2}\): Multiplos de 5 entre 1 y 50
Todos los múltiplos de\(5\) extremo con cualquiera\(5\) o\(0\). Así como identificamos múltiplos\(2\) de mirando el último dígito, podemos identificar múltiplos\(5\) de mirando el último dígito.
Determine si cada uno de los siguientes es un múltiplo de\(5\):
- \(579\)
- \(880\)
Solución
| ¿El 579 es múltiplo de 5? | |
| ¿El último dígito es 5 o 0? | No. |
| 579 no es múltiplo de 5. |
| ¿El 880 es un múltiplo de 5? | |
| ¿El último dígito es 5 o 0? | Sí. |
| 880 no es múltiplo de 5. |
Determinar si cada número es un múltiplo de\(5\).
- \(675\)
- \(1,578\)
- Contestar a
-
si
- Respuesta b
-
no
Determinar si cada número es un múltiplo de\(5\).
- \(421\)
- \(2,690\)
- Contestar a
-
no
- Respuesta b
-
si
La figura\(\PageIndex{3}\) destaca los múltiplos de\(10\) entre\(1\) y\(50\). Todos los múltiplos de\(10\) todos terminan con un cero.
Figura\(\PageIndex{3}\): Multiplos de 10 entre 1 y 50
Determine si cada uno de los siguientes es un múltiplo de\(10\):
- \(425\)
- \(350\)
Solución
| ¿El 425 es un múltiplo de 10? | |
| ¿El último dígito es cero? | No. |
| 425 no es múltiplo de 10. |
| ¿350 es múltiplo de 10? | |
| ¿El último dígito es cero? | Sí. |
| 350 es un múltiplo de 10. |
Determine si cada número es un múltiplo de\(10\):
- \(179\)
- \(3,540\)
- Contestar a
-
no
- Respuesta b
-
si
Determine si cada número es un múltiplo de\(10\):
- \(110\)
- \(7,595\)
- Contestar a
-
si
- Respuesta b
-
no
La figura\(\PageIndex{4}\) destaca múltiplos de\(3\). El patrón para múltiplos de no\(3\) es tan obvio como los patrones para múltiplos de\(2\),\(5\), y\(10\).
Figura\(\PageIndex{4}\): Multiplos de 3 entre 1 y 50
A diferencia de los otros patrones que hemos examinado hasta ahora, este patrón no involucra el último dígito. El patrón para múltiplos de\(3\) se basa en la suma de los dígitos. Si la suma de los dígitos de un número es un múltiplo de\(3\), entonces el número en sí es un múltiplo de\(3\). Ver Tabla\(\PageIndex{2}\).
| Múltiple de 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
|---|---|---|---|---|---|---|---|---|
| Suma de dígitos | 3 | 6 | 9 |
1 + 2 3 |
1 + 5 6 |
1 + 8 9 |
2 + 1 3 |
2 + 4 6 |
Considera el número\(42\). Los dígitos son\(4\) y\(2\), y su suma es\(4 + 2 = 6\). Ya que\(6\) es un múltiplo de\(3\), sabemos que también\(42\) es un múltiplo de\(3\).
Determine si cada uno de los números dados es un múltiplo de\(3\):
- \(645\)
- \(10,519\)
Solución
- ¿Es\(645\) un múltiplo de\(3\)?
| Encuentra la suma de los dígitos. | 6 + 4 + 5 = 15 |
| ¿15 es un múltiplo de 3? | Sí. |
| Si no estamos seguros, podríamos agregar sus dígitos para averiguarlo. Podemos verificarlo dividiendo 645 por 3. | 645 ÷ 3 |
| El cociente es de 215. | 3 • 215 = 645 |
- ¿Es\(10,519\) un múltiplo de\(3\)?
| Encuentra la suma de los dígitos. | 1 + 0 + 5 + 1 + 9 = 16 |
| ¿15 es un múltiplo de 3? | No. |
| Así que 10,519 tampoco es un múltiplo de 3.. | 645 ÷ 3 |
| Podemos verificar esto dividiendo entre 10,519 por 3. |  |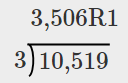
Cuando dividimos\(10,519\) por\(3\), no obtenemos un número de conteo, así que no\(10,519\) es producto de un número de conteo y\(3\). No es un múltiplo de\(3\).
Determine si cada número es un múltiplo de\(3\):
- \(954\)
- \(3,742\)
- Contestar a
-
si
- Respuesta b
-
no
Determine si cada número es un múltiplo de\(3\):
- \(643\)
- \(8,379\)
- Contestar a
-
no
- Respuesta b
-
si
Mira hacia atrás en los gráficos donde destacaste los múltiplos de\(2\), de\(5\), y de\(10\). Observe que los múltiplos de\(10\) son los números que son múltiplos de ambos\(2\) y\(5\). Eso es porque\(10 = 2 • 5\). De igual manera, ya que\(6 = 2 • 3\), los múltiplos de\(6\) son los números que son múltiplos de ambos\(2\) y\(3\).
Usar pruebas comunes de divisibilidad
Otra forma de decir que\(375\) es un múltiplo de\(5\) es decir que\(375\) es divisible por\(5\). De hecho,\(375 ÷ 5\) es\(75\), así\(375\) es\(5 • 75\). Observe en Ejemplo\(\PageIndex{4}\) que no\(10,519\) es un múltiplo\(3\). Cuando nos\(3\) dividimos\(10,519\) por no conseguimos un número de conteo, así que no\(10,519\) es divisible por\(3\).
Si un número\(m\) es un múltiplo de\(n\), entonces decimos que\(m\) es divisible por\(n\).
Dado que la multiplicación y la división son operaciones inversas, los patrones de múltiplos que encontramos pueden ser utilizados como pruebas de divisibilidad. El cuadro\(\PageIndex{3}\) resume las pruebas de divisibilidad para algunos de los números de conteo entre uno y diez.
| Un número es divisible por | |
|---|---|
| 2 | si el último dígito es 0, 2, 4, 6 u 8 |
| 3 | si la suma de los dígitos es divisible por 3 |
| 5 | si el último dígito es 5 o 0 |
| 6 | si es divisible por 2 y 3 |
| 10 | si el último dígito es 0 |
Determinar si\(1,290\) es divisible por\(2\)\(3\),\(5\), y\(10\).
Solución
Tabla\(\PageIndex{4}\) aplica las pruebas de divisibilidad a\(1,290\). En la columna del extremo derecho, verificamos los resultados de las pruebas de divisibilidad viendo si el cociente es un número entero.
| Divisible por...? | Test | ¿Divisible? | Cheque |
|---|---|---|---|
| 2 | ¿El último dígito es 0, 2, 4, 6 u 8? | si | 1290 ÷ 2 = 645 |
| 3 |
¿La suma de dígitos es divisible por 3? 1 + 2 + 9 + 0 = 12 |
si | 1290 ÷ 3 = 430 |
| 5 | ¿El último dígito es 5 o 0? | si | 1290 ÷ 5 = 258 |
| 10 | ¿El último dígito es 0? | si | 1290 ÷ 10 = 129 |
Así,\(1,290\) es divisible por\(2\),\(3\),\(5\), y\(10\).
Determine si el número dado es divisible por\(2\)\(3\),\(5\), y\(10\).
\(6240\)
- Contestar
-
Divisible por\(2\),\(3\),\(5\), y\(10\)
Determine si el número dado es divisible por\(2\)\(3\),\(5\), y\(10\).
\(7248\)
- Contestar
-
Divisible por\(2\) y\(3\), no\(5\) o\(10\)
Determinar si\(5,625\) es divisible por\(2\)\(3\),\(5\), y\(10\).
Solución
Tabla\(\PageIndex{5}\) aplica las pruebas de divisibilidad\(5,625\) y prueba los resultados encontrando los cocientes.
| Divisible por...? | Test | ¿Divisible? | Cheque |
|---|---|---|---|
| 2 | ¿El último dígito es 0, 2, 4, 6 u 8? | no | 5625 ÷ 2 = 2812.5 |
| 3 |
¿La suma de dígitos es divisible por 3? 5 + 6 + 2 + 5 = 18 |
si | 5625 ÷ 3 = 1875 |
| 5 | ¿El último dígito es 5 o 0? | si | 5625 ÷ 5 = 1125 |
| 10 | ¿El último dígito es 0? | no | 5625 ÷ 10 = 562.5 |
Así,\(5,625\) es divisible por\(3\) y\(5\), pero no\(2\), o\(10\).
Determine si el número dado es divisible por\(2\)\(3\),\(5\), y\(10\).
\(4962\)
- Contestar
-
Divisible por\(2\),\(3\), no\(5\) o\(10\)
Determine si el número dado es divisible por\(2\)\(3\),\(5\), y\(10\).
\(3765\)
- Contestar
-
Divisible por\(3\) y\(5\)
Encuentra todos los factores de un número
A menudo hay varias formas de hablar de la misma idea. Hasta el momento, hemos visto que si\(m\) es un múltiplo de\(n\), podemos decir que\(m\) es divisible por\(n\). Sabemos que\(72\) es producto de\(8\) y\(9\), así podemos decir que\(72\) es un múltiplo de\(8\) y\(72\) es un múltiplo de\(9\). También podemos decir que\(72\) es divisible por\(8\) y por\(9\). Otra forma de hablar de esto es decir eso\(8\) y\(9\) son factores de\(72\). Cuando\(72 = 8 ⋅ 9\) escribimos podemos decir que hemos factorizado\(72\).
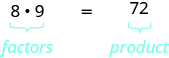
Si\(a • b = m\), entonces\(a\) y\(b\) son factores de\(m\), y\(m\) es producto de\(a\) y\(b\).
En álgebra, puede ser útil determinar todos los factores de un número. Esto se llama factorizar un número, y puede ayudarnos a resolver muchos tipos de problemas.
Por ejemplo, supongamos que un coreógrafo está planeando un baile para un recital de ballet. Hay 24 bailarines, y para cierta escena, el coreógrafo quiere organizar a los bailarines en grupos de igual tamaño en el escenario.
¿De cuántas maneras se puede poner a los bailarines en grupos de igual tamaño? Responder a esta pregunta es lo mismo que identificar los factores de\(24\). Tabla\(\PageIndex{6}\) resume las diferentes formas en que el coreógrafo puede organizar a los bailarines.
| Número de grupos | Bailarines por Grupo | Total Bailarines |
|---|---|---|
| 1 | 24 | 1 • 24 = 24 |
| 2 | 12 | 2 • 12= 24 |
| 3 | 8 | 3 • 8= 24 |
| 4 | 6 | 4 • 6= 24 |
| 6 | 4 | 6 • 4= 24 |
| 8 | 3 | 8 • 3= 24 |
| 12 | 2 | 12 • 2= 24 |
| 24 | 1 | 24 • 1= 24 |
¿Qué patrones ves en Table\(\PageIndex{6}\)? ¿Te diste cuenta que el número de grupos por el número de bailarines por grupo es siempre\(24\)? Esto tiene sentido, ya que siempre hay\(24\) bailarines.
Puede notar otro patrón si observa cuidadosamente las dos primeras columnas. Estas dos columnas contienen exactamente el mismo conjunto de números, pero en orden inverso. Son espejos el uno del otro, y de hecho, ambas columnas enumeran todos los factores de\(24\), que son:
\(1, 2, 3, 4, 6, 8, 12, 24\)
Podemos encontrar todos los factores de cualquier número de conteo dividiendo sistemáticamente el número por cada número de conteo, empezando por\(1\). Si el cociente es también un número de conteo, entonces el divisor y el cociente son factores del número. Podemos detenernos cuando el cociente se vuelve más pequeño que el divisor.
Paso 1. Divida el número por cada uno de los números de conteo, en orden, hasta que el cociente sea menor que el divisor.
- Si el cociente es un número de conteo, el divisor y el cociente son un par de factores.
- Si el cociente no es un número de conteo, el divisor no es un factor.
Paso 2. Enumere todos los pares de factores.
Paso 3. Escribe todos los factores en orden de menor a mayor.
Encuentra todos los factores de\(72\).
Solución
Dividir\(72\) por cada uno de los números de conteo comenzando con\(1\). Si el cociente es un número entero, el divisor y el cociente son un par de factores.
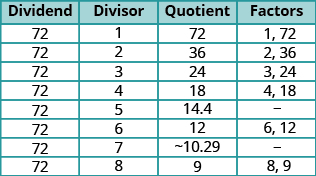
La siguiente línea tendría un divisor de\(9\) y un cociente de\(8\). El cociente sería menor que el divisor, así que paramos. Si continuamos, terminaríamos enumerando solo los mismos factores nuevamente en orden inverso. Enumerando todos los factores de menor a mayor, tenemos\(1\),,\(2\),\(3\),\(4\),\(6\),\(8\),\(9\),\(12\),\(18\),,\(24\),\(36\), y\(72\).
Encuentra todos los factores del número dado:\(96\)
- Contestar
-
\(1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96\)
Encuentra todos los factores del número dado:\(80\)
- Contestar
-
\(1, 2, 4, 5, 8, 10, 16, 20, 40, 80\)