2.9: Factorización de Prime y el Múltiple Mínimo Común (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114265

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Encuentra la factorización primo de un número compuesto
Encuentra el múltiplo mínimo común (MCM) de dos números

¡prepárate!

Antes de comenzar, toma este cuestionario de preparación.

¿Es$810$ divisible por$2, 3, 5, 6,$ o$10$? Si te perdiste este problema, revisa el Ejemplo 2.4.5.
¿Es$127$ primo o compuesto? Si te perdiste este problema, revisa el Ejemplo 2.4.8.
Escribir$2 • 2 • 2 • 2$ en notación exponencial. Si te perdiste este problema, revisa el Ejemplo 2.1.5.

Encuentre la factorización principal de un número compuesto

En el apartado anterior, encontramos los factores de un número. Los números primos tienen sólo dos factores, el número$1$ y el número primo en sí. Los números compuestos tienen más de dos factores, y cada número compuesto se puede escribir como un producto único de primos. A esto se le llama la factorización prima de un número. Cuando escribimos la factorización prima de un número, estamos reescribiendo el número como producto de primos. Encontrar la factorización primo de un número compuesto te ayudará más adelante en este curso.

Definición: Factorización Prime

La desfactorización de un número es el producto de números primos que es igual al número.

Es posible que desee hacer referencia a la siguiente lista de números primos menos que a$50$ medida que trabaja a través de esta sección.

$2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47$

Factorización Prime Usando el Método de Árbol de Factores

Una forma de encontrar la factorización prima de un número es hacer un árbol de factores. Comenzamos por escribir el número, y luego escribirlo como producto de dos factores. Escribimos los factores debajo del número y los conectamos al número con un segmento de línea pequeña, una “rama” del árbol factorial.

Si un factor es primo, lo rodeamos (como un brote en un árbol), y no factorizamos esa “rama” más allá. Si un factor no es primo, repetimos este proceso, escribiéndolo como producto de dos factores y agregando nuevas ramas al árbol.

Seguimos hasta que todas las ramas terminen con un prime. Cuando el árbol factorial está completo, los primos rodeados nos dan la factorización principal.

Por ejemplo, encontremos la factorización principal de$36$. Podemos comenzar con cualquier par de factores como$3$ y$12$. Escribimos$3$ y$12$ a continuación$36$ con sucursales conectándolos.

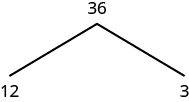
El factor$3$ es primo, así que lo rodeamos. El factor$12$ es compuesto, por lo que necesitamos encontrar sus factores. Vamos a usar$3$ y$4$. Escribimos estos factores en el árbol bajo el$12$.

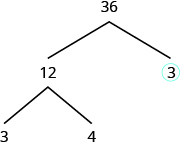
El factor$3$ es primo, así que lo rodeamos. El factor$4$ es compuesto, y factoriza en$2 • 2$. Escribimos estos factores bajo el$4$. Ya que$2$ es primo, rodeamos ambos$2s$.

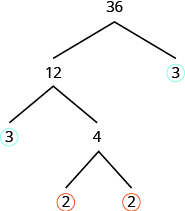
$La figura muestra un árbol factorial con el número 36 en la parte superior. Dos ramas se están dividiendo de menos de 36. La rama derecha tiene un número 3 al final con un círculo alrededor de ella. El ramal izquierdo tiene el número 12 al final. Dos ramas más se están separando de las menores de 12. La rama derecha tiene el número 4 al final y la rama izquierda tiene el número 3 al final con un círculo alrededor de ella. Dos ramas más se están separando de las menores de 4. Tanto la rama izquierda como la derecha tienen el número 2 al final con un círculo alrededor de ella.$

La factorización prima es el producto de los primos en círculo. Generalmente escribimos la factorización prima en orden de menor a mayor.

$2 \cdot 2 \cdot 3 \cdot 3$

En casos como este, donde se repiten algunos de los factores primos, podemos escribir la factorización prima en forma exponencial.

$2 \cdot 2 \cdot 3 \cdot 3$

$2^{2} \cdot 3^{2}$

Tenga en cuenta que podríamos haber comenzado nuestro árbol de factores con cualquier par de factores de$36$. Elegimos$12$ y$3$, pero el mismo resultado hubiera sido el mismo si hubiéramos empezado con$2$ y$18$,$4$ y$9$, o$6$ y y$6$.

CÓMO: ENCONTRAR LA FACTORIZACIÓN PRIMERA DE UN NÚMERO COMPUESTO USANDO EL

Paso 1. Encuentra cualquier par de factores del número dado, y usa estos números para crear dos ramas.
Paso 2. Si un factor es primo, esa rama está completa. Da un círculo a la prima.
Paso 3. Si un factor no es primo, escríbelo como producto de un par de factores y continúe con el proceso.
Paso 4. Escriba el número compuesto como el producto de todos los primos en un círculo.

Ejemplo$\PageIndex{1}$: prime factors

Encuentre la factorización principal del$48$ uso del método del árbol de factores.

Solución

Podemos iniciar nuestro árbol usando cualquier par de factores de 48. Usemos 2 y 24. Damos un círculo al 2 porque es primo y así esa rama está completa.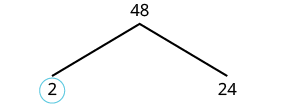
Ahora vamos a facturar 24. Usemos 4 y 6.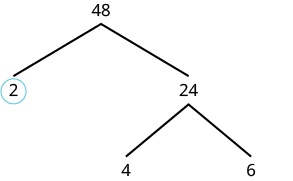
Ninguno de los dos factores es primo, por lo que tampoco hacemos un círculo. Se factoriza el 4, usando 2 y 2. Nosotros factorizamos 6, usando 2 y 3. Damos un círculo a los 2s y a los 3 ya que son primos. Ahora todas las ramas terminan en un prime.
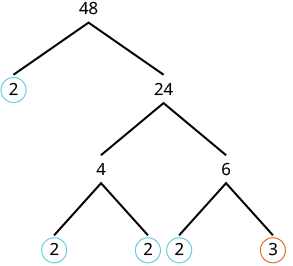Escribe el producto de los números con un círculo.	2 • 2 • 2 • 2 • 3
Escribir en forma exponencial.	2 ⁴ • 3

Comprueba esto por tu cuenta multiplicando todos los factores juntos. El resultado debe ser$48$.

Ejercicio$\PageIndex{1}$

Encuentra la factorización principal usando el método de árbol de factores:$80$

Contestar: $2 \cdot 2 \cdot 2 \cdot 2 \cdot 5, \text { or } 2^4 \cdot 5$

Ejercicio$\PageIndex{2}$

Encuentra la factorización principal usando el método de árbol de factores:$60$

Contestar: $2 \cdot 2 \cdot 3 \cdot 5, \text { or } 2^2 \cdot 3 \cdot 5$

Ejemplo$\PageIndex{2}$: prime factors

Encuentre la factorización principal del$84$ uso del método del árbol de factores.

Solución

Empezamos con el par de factores 4 y 21. Ninguno de los dos factores es primo así que los factorizamos más.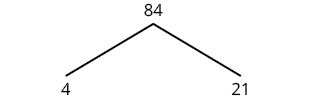
Ahora los factores son todos primos, así que los rodeamos.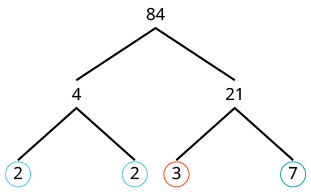
Entonces escribimos 84 como producto de todos los primos rodeados.	2 • 2 • 3 • 7 = 2 ² • 3 • 7

Dibuja un árbol factorial de$84$.

Ejercicio$\PageIndex{3}$

Encuentra la factorización principal usando el método de árbol de factores:$126$

Contestar: $2 \cdot 3 \cdot 3 \cdot 7, \text { or } 2 \cdot 3^2 \cdot 7$

Ejercicio$\PageIndex{4}$

Encuentra la factorización principal usando el método de árbol de factores:$294$

Contestar: $2 \cdot 3 \cdot 7 \cdot 7, \text { or } 2 \cdot 3 \cdot 7^2$

Factorización Prime Usando el Método Ladder

El método de escalera es otra forma de encontrar los factores primos de un número compuesto. Conduce al mismo resultado que el método del árbol factorial. Algunas personas prefieren el método de escalera al método del árbol factorial, y viceversa.

Para comenzar a construir la “escalera”, divida el número dado por su factor primo más pequeño. Por ejemplo, para iniciar la escalera para$36$, dividimos$36$ por$2$, el factor primo más pequeño de$36$.

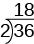
Para agregar un “escalón” a la escalera, seguimos dividiendo por el mismo primo hasta que ya no se divida uniformemente.

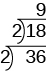
$En la imagen se muestra la división de 2 en 36 para obtener el cociente 18. Esta división se representa usando un soporte de división con 2 en el exterior izquierdo del soporte, 36 dentro del soporte y 18 por encima del 36, fuera del soporte. Otro soporte de división se escribe alrededor del 18 con un 2 en el exterior izquierdo del soporte y un 9 por encima del 18, fuera del corchete.$

Entonces dividimos por el próximo primo; así dividimos$9$ por$3$.

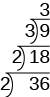
Seguimos dividiendo la escalera de esta manera hasta que el cociente sea primo. Dado que el cociente,$3$, es primo, nos detenemos aquí. ¿Ves por qué el método de escalera a veces se llama división apilada?

La factorización principal es el producto de todos los primos en los lados y la parte superior de la escalera.

$2 \cdot 2 \cdot 3 \cdot 3$

$2^{2} \cdot 3^{2}$

Observe que el resultado es el mismo que obtuvimos con el método del árbol factorial.

CÓMO: ENCONTRAR LA FACTORIZACIÓN PRIMERA DE UN NUMERO COMPUESTO USANDO EL MÉTODO

Paso 1. Divide el número por el primo más pequeño.

Paso 2. Continúa dividiendo por ese primo hasta que ya no se divida uniformemente.

Paso 3. Divide por el siguiente primo hasta que ya no se divida de manera uniforme.

Paso 4. Continuar hasta que el cociente sea primo.

Paso 5. Escriba el número compuesto como producto de todos los primos en los lados y la parte superior de la escalera.

Ejemplo$\PageIndex{3}$: prime factors

Encuentra la factorización principal del$120$ uso del método de escalera.

Solución

Divida el número por el primo más pequeño, que es 2.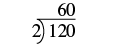
Continúa dividiendo por 2 hasta que ya no se divida uniformemente.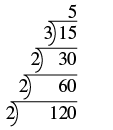
Dividir por el próximo primo, 3.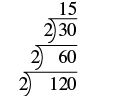
El cociente, 5, es primo, por lo que la escalera está completa. Escribe la factorización prime de 120.	2 • 2 • 2 • 3 • 5 2 ³ • 3 • 5

Compruébalo tú mismo multiplicando los factores. El resultado debe ser$120$.

Ejercicio$\PageIndex{5}$

Encuentra la factorización principal usando el método de escalera:$80$

Contestar: $2 \cdot 2 \cdot 2 \cdot 2 \cdot 5, \text { or } 2^4 \cdot 5$

Ejercicio$\PageIndex{6}$

Encuentra la factorización principal usando el método de escalera:$60$

Contestar: $2 \cdot 2 \cdot 3 \cdot 5, \text { or } 2^2 \cdot 3 \cdot 5$

Ejemplo$\PageIndex{4}$: prime factors

Encuentra la factorización principal del$48$ uso del método de escalera.

Solución

Divida el número por el primo más pequeño, 2.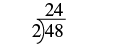

Continúa dividiendo por 2 hasta que ya no se divida uniformemente.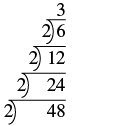

El cociente, 3, es primo, por lo que la escalera está completa. Escribe la factorización prime de 48.

$2 • 2 • 2 • 2 • 3$

$2^4 • 3$

Ejercicio$\PageIndex{7}$

Encuentra la factorización principal usando el método de escalera:$126$

Contestar: $2 \cdot 3 \cdot 3 \cdot 7, \text { or } 2 \cdot 3^2 \cdot 7$

Ejercicio$\PageIndex{8}$

Encuentra la factorización principal usando el método de escalera:$294$

Contestar: $2 \cdot 3 \cdot 7 \cdot 7, \text { or } 2 \cdot 3 \cdot 7^2$

Colaboradores y Atribuciones

Template:ContribElementaryAlgebraOpenStax

Search

Definición: Factorización Prime

CÓMO: ENCONTRAR LA FACTORIZACIÓN PRIMERA DE UN NÚMERO COMPUESTO USANDO EL

Ejemplo\(\PageIndex{1}\): prime factors

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{2}\): prime factors

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

CÓMO: ENCONTRAR LA FACTORIZACIÓN PRIMERA DE UN NUMERO COMPUESTO USANDO EL MÉTODO

Ejemplo\(\PageIndex{3}\): prime factors

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejemplo\(\PageIndex{4}\): prime factors

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)