2.S: Introducción al Lenguaje del Álgebra (Resumen)

Términos Clave

coeficiente	La constante que multiplica la (s) variable (s) en un término.
número compuesto	Un número compuesto es un número de conteo que no es primo.
divisibilidad	Si un número m es un múltiplo de n, entonces decimos que m es divisible por n.
ecuación	Una ecuación se compone de dos expresiones conectadas por un signo igual.
evaluar	Evaluar una expresión algebraica significa encontrar el valor de la expresión cuando la variable es reemplazada por un número dado.
expresión	Una expresión es un número, una variable o una combinación de números y variables y símbolos de operación.
mínimo común múltiplo (MCM)	El número más pequeño que es un múltiplo de dos números.
términos similares	Términos que son constantes o tienen las mismas variables con los mismos exponentes.
múltiplo de un número	Un número es un múltiplo de n si es producto de un número de conteo y n.
factorización prima	El producto de números primos que es igual al número.
número primo	Un número de conteo mayor a 1 cuyos únicos factores son 1 y en sí mismo.
solución de una ecuación	Un valor de una variable que hace una declaración verdadera cuando se sustituye en la ecuación. El proceso de encontrar la solución a una ecuación se llama resolver la ecuación.
término	Una constante o producto de una constante y una o más variables.

Conceptos clave

2.1 - Utilizar el lenguaje del álgebra

Operación	Notación	Decir:	El resultado es...
Adición	a + b	a más b	La suma de a y b
Multiplicación	a • b, (a) (b), (a) b, a (b)	a veces b	El producto de a y b
Resta	a - b	a menos b	La diferencia de a y b
División	a ÷ b, a/b,\(\dfrac{a}{b}\),\(b \overline{)a}\)	a dividido por b	El cociente de a y b

• Símbolo de igualdad
  • a = b se lee como a es igual a b
  • El símbolo = se llama el signo igual.
• Desigualdad
  • a < b se lee a es menor que b
  • a está a la izquierda de b en la recta numérica:
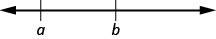
  • a > b se lee a es mayor que b
  • a está a la derecha de b en la recta numérica:

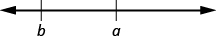
Cuadro 2.77

Notación algebraica	Decir
a = b	a es igual a b
a ≠ b	a no es igual a b
a < b	a es menor que b
a > b	a es mayor que b
a ≤ b	a es menor o igual que b
a ≥ b	a es mayor o igual que b

• Notación exponencial
  • Para cualquier expresión a n es un factor multiplicado por sí mismo n veces, si n es un entero positivo.
  • a ⁿ significa multiplicar n factores de a
  • La expresión de una ⁿ se lee a la n ^ésima potencia

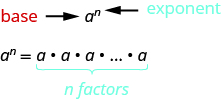
• Orden de Operaciones: Al simplificar expresiones matemáticas, realice las operaciones en el siguiente orden:

1. Paréntesis y otros símbolos de agrupación: Simplifique todas las expresiones dentro de los paréntesis u otros símbolos de agrupación, trabajando primero en los paréntesis más internos.
2. Exponentes: Simplifica todas las expresiones con exponentes.
3. Multiplicación y División: Realiza todas las multiplicaciones y divisiones en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
4. Suma y resta: Realiza todas las sumas y restas en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.

2.2 - Evaluar, simplificar y traducir expresiones

• Combina términos similares.

1. Identificar términos similares.
2. Reorganizar la expresión para que los términos estén juntos.
3. Agregar los coeficientes de los términos similares

2.3 - Resolver ecuaciones usando las propiedades de resta y suma de la igualdad

• Determinar si un número es una solución a una ecuación.

1. Sustituir el número por la variable en la ecuación.
2. Simplifica las expresiones en ambos lados de la ecuación.
3. Determinar si la ecuación resultante es verdadera. Si es cierto, el número es una solución. Si no es cierto, el número no es una solución.

• Resta Propiedad de Igualdad
  • Para cualquier número a, b y c, si a = b, entonces a - c = b - c.

• Resuelve una ecuación usando la Propiedad de Sustracción de Igualdad.

1. Utilice la Propiedad de Sustracción de Igualdad para aislar la variable.
2. Simplifica las expresiones en ambos lados de la ecuación.
3. Consulta la solución.

• Adición Propiedad de Igualdad
  • Para cualquier número a, b y c, si a = b, entonces a + c = b + c.
• Resolver una ecuación usando la Propiedad de Suma de Igualdad.

1. Utilice la Propiedad de Suma de Igualdad para aislar la variable.
2. Simplifica las expresiones en ambos lados de la ecuación.
3. Consulta la solución.

2.4 - Encuentra múltiplos y factores

Pruebas de Divisibilidad
Un número es divisible por
2	si el último dígito es 0, 2, 4, 6 u 8
3	si la suma de los dígitos es divisible por 3
5	si el último dígito es 5 o 0
6	si es divisible por 2 y 3
10	si el último dígito es 0

• Factores: Si a • b = m, entonces a y b son factores de m, y m es el producto de a y b.
• Encuentra todos los factores de un número de conteo.

1. Divida el número por cada uno de los números de conteo, en orden, hasta que el cociente sea menor que el divisor.
   1. Si el cociente es un número de conteo, el divisor y el cociente son un par de factores.
   2. Si el cociente no es un número de conteo, el divisor no es un factor.
2. Enumere todos los pares de factores.
3. Escribe todos los factores en orden de menor a mayor.

• Determina si un número es primo.

1. Pruebe cada uno de los primos, en orden, para ver si es un factor del número.
2. Comience con 2 y deténgase cuando el cociente sea menor que el divisor o cuando se encuentre un factor primo.
3. Si el número tiene un factor primo, entonces es un número compuesto. Si no tiene factores primos, entonces el número es primo.

2.5 - Factorización Prime y el Múltiple Mínimo Común

• Encuentre la factorización primo de un número compuesto usando el método de árbol.

1. Encuentra cualquier par de factores del número dado, y usa estos números para crear dos ramas.
2. Si un factor es primo, esa rama está completa. Encierra en círculo el prime.
3. Si un factor no es primo, escríbelo como producto de un par de factores y continúe con el proceso.
4. Escriba el número compuesto como el producto de todos los primos en un círculo.

• Encuentre la factorización primo de un número compuesto usando el método de escalera.

1. Divide el número por el primo más pequeño.
2. Continúa dividiendo por ese primo hasta que ya no se divida uniformemente.
3. Divide por el siguiente primo hasta que ya no se divida uniformemente.
4. Continuar hasta que el cociente sea primo.
5. Escriba el número compuesto como producto de todos los primos en los lados y la parte superior de la escalera.

• Encuentra el LCM enumerando múltiplos

1. Enumere los primeros varios múltiplos de cada número.
2. Busque múltiplos comunes a ambas listas. Si no hay múltiplos comunes en las listas, escriba múltiplos adicionales para cada número.
3. Busque el número más pequeño que sea común a ambas listas.
4. Este número es el LCM.

• Encuentra el LCM usando el método de factores primos.

1. Encuentra la factorización primo de cada número.
2. Escribe cada número como producto de primos, haciendo coincidir los primos verticalmente cuando sea posible.
3. Baje los primos en cada columna.
4. Multiplica los factores para obtener el LCM.

Colaboradores y Atribuciones