Inicio
Matemáticas
Pre-Álgebra
Libro: Preálgebra (OpenStax)
3: Enteros
3.1: Introducción a los números enteros (Parte 1)

3.1: Introducción a los números enteros (Parte 1)

Última actualización
Guardar como PDF

Page ID: 114217

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Localizar números positivos y negativos en la recta numérica
Ordenar números positivos y negativos
Encuentra opuestos
Simplificar expresiones con valor absoluto
Traducir frases de palabras a expresiones con enteros

¡prepárate!

Antes de comenzar, toma este cuestionario de preparación.

Trazar$0$,$1$, y$3$ en una recta numérica. Si te perdiste este problema, revisa el Ejemplo 1.1.1.
Rellena el símbolo correspondiente: ($=$$<$, o$>$):$2$ ___$4$ Si te perdiste este problema, revisa el Ejemplo 2.1.2.

Localizar números positivos y negativos en la línea numérica

¿Vives en un lugar que tiene inviernos muy fríos? ¿Alguna vez has experimentado una temperatura bajo cero? Si es así, ya estás familiarizado con los números negativos. Un número negativo es un número que es menor que$0$. Las temperaturas muy frías se miden en grados bajo cero y pueden describirse por números negativos. Por ejemplo,$-1^{\circ}$ F (leer como “negativo un grado Fahrenheit”) es$1$ grado por debajo$0$. Se muestra un signo menos antes de un número para indicar que es negativo. La figura$\PageIndex{1}$ muestra$-20^{\circ}$ F, que es$20$ grados por debajo$0$.

$Esta figura es un termómetro escalado en grados Fahrenheit. El termómetro tiene una lectura de 20 grados.$

Figura$\PageIndex{1}$: Las temperaturas por debajo de cero se describen por números negativos.

Las temperaturas no son los únicos números negativos. Un sobregiro bancario es otro ejemplo de un número negativo. Si una persona escribe un cheque por más de lo que tiene en su cuenta, su saldo será negativo.

Las elevaciones también pueden ser representadas por números negativos. La elevación a nivel del mar es de$0$ pies. Las elevaciones sobre el nivel del mar son positivas y las elevaciones por debajo del nivel del mar son negativas. La elevación del Mar Muerto, que limita con Israel y Jordania, está a unos$1,302$ pies por debajo del nivel del mar, por lo que la elevación del Mar Muerto se puede representar como$−1,302$ pies. Ver Figura$\PageIndex{2}$.

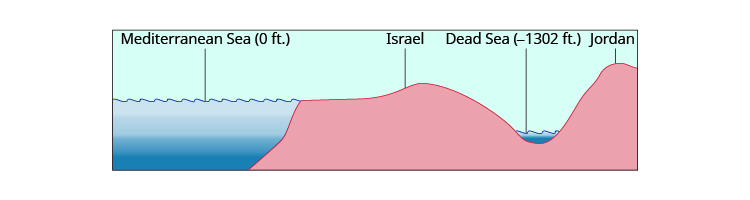
$Esta figura es un dibujo de una vista lateral de la costa de Israel, mostrando diferentes elevaciones. El Mar Mediterráneo está etiquetado 0 pies de elevación y el Mar Muerto está etiquetado como negativo 1302 pies de elevación. El país de Jordania también está etiquetado en la figura.$

Figura$\PageIndex{2}$: La superficie del mar Mediterráneo tiene una elevación de 0 pies. El diagrama muestra que las montañas cercanas tienen elevaciones más altas (positivas) mientras que el Mar Muerto tiene una elevación menor (negativa).

Las profundidades por debajo de la superficie oceánica también se describen por números negativos. Un submarino, por ejemplo, podría descender a una profundidad de$500$ pies. Su posición sería entonces$−500$ pies como se etiqueta en la Figura$\PageIndex{3}$.

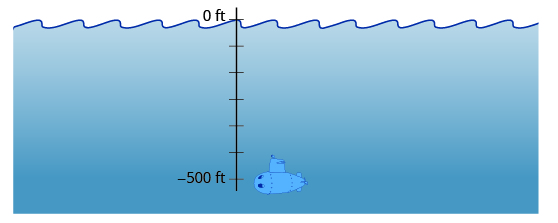
$Esta figura es un dibujo de un submarino bajo el agua. En el agua también hay una línea numérica vertical, escalada en pies. La línea numérica tiene 0 pies en la superficie y menos 500 pies por debajo del agua donde se encuentra el submarino.$

Figura$\PageIndex{3}$: Las profundidades bajo el nivel del mar se describen por números negativos. Un submarino a 500 pies bajo el nivel del mar está a −500 pies.

Tanto los números positivos como los negativos se pueden representar en una recta numérica. Recordemos que la línea numérica creada en Agregar números enteros comenzó en$0$ y mostró los números de conteo aumentando a la derecha como se muestra en la Figura$\PageIndex{4}$. Los números de conteo ($1, 2, 3, …$) en la recta numérica son todos positivos. Podríamos escribir un signo más,$+$, antes de un número positivo como$+2$ o$+3$, pero es costumbre omitir el signo más y escribir sólo el número. Si no hay señal, se supone que el número es positivo.

$Esta cifra es una línea numérica escalada de 0 a 6.$

Figura$\PageIndex{4}$

Ahora necesitamos extender la línea numérica para incluir números negativos. Marcamos varias unidades a la izquierda de cero, manteniendo los intervalos del mismo ancho que los del lado positivo. Etiquetamos las marcas con números negativos, comenzando por$-1$ en la primera marca a la izquierda de$0, -2$ en la siguiente marca, y así sucesivamente. Ver Figura$\PageIndex{5}$.

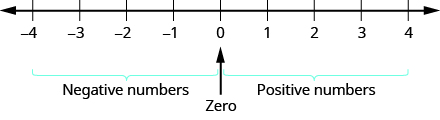
$Esta cifra es una recta numérica con 0 en el medio. Entonces, el escalado tiene números positivos 1 a 4 a la derecha de 0 y números negativos, negativo 1 a negativo 4 a la izquierda de 0.$

Figura$\PageIndex{5}$: En una recta numérica, los números positivos están a la derecha de cero. Los números negativos están a la izquierda de cero. ¿Qué pasa con el cero? El cero no es ni positivo ni negativo.

Las flechas en cada extremo de la línea indican que la recta numérica se extiende para siempre en cada dirección. No hay mayor número positivo y no hay menor número negativo.

Ejemplo$\PageIndex{1}$: plot on the number line

Trazar los números en una recta numérica:

$3$
$-3$
$-2$

Solución

Dibuja una recta numérica. Marcar$0$ en el centro y etiquetar varias unidades a la izquierda y derecha.

Para trazar$3$, comience en$0$ y cuente tres unidades a la derecha. Coloque un punto como se muestra en la Figura$\PageIndex{6}$.

$Esta cifra es una recta numérica escalada del 4 al 4 negativo, con el punto 3 etiquetado con un punto.$

Figura$\PageIndex{6}$

Para trazar$-3$, comenzar en$0$ y contar tres unidades a la izquierda. Coloque un punto como se muestra en la Figura$\PageIndex{7}$.

$Esta cifra es una línea numérica escalada de 4 a 4 negativo, con el punto negativo 3 etiquetado con un punto.$

Figura$\PageIndex{7}$

Para trazar$-2$, comience en$0$ y cuente dos unidades a la izquierda. Coloque un punto como se muestra en la Figura$\PageIndex{8}$.

$Esta cifra es una línea numérica escalada de 4 a 4 negativo, con el punto negativo 2 etiquetado con un punto.$

Figura$\PageIndex{8}$

Ejercicio$\PageIndex{1}$

Trazar los números en una recta numérica.

$1$,$-1$,$-4$

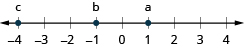
Contestar: $CNX_BMath_Figure_03_01_010_img.jpg$

Ejercicio$\PageIndex{2}$

Trazar los números en una recta numérica.

$-4$,$4$,$-1$

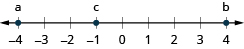
Contestar: $CNX_BMath_Figure_03_01_011_img.jpg$

Orden de números positivos y negativos

Podemos usar la línea numérica para comparar y ordenar números positivos y negativos. Al ir de izquierda a derecha, los números aumentan de valor. Al ir de derecha a izquierda, los números disminuyen de valor. Ver Figura$\PageIndex{9}$.

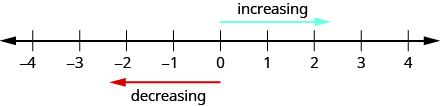
$Esta cifra es una línea numérica. Por encima de la recta numérica hay una flecha apuntando a la derecha etiquetada como creciente. Debajo de la recta numérica hay una flecha que apunta a la izquierda etiquetada como decreciente.$

Figura$\PageIndex{9}$

Así como lo hicimos con los números positivos, podemos usar símbolos de desigualdad para mostrar el orden de los números positivos y negativos. Recuerda que usamos la notación$a < b$ (leer$a$ es menor que$b$) cuando$a$ está a la izquierda de$b$ en la recta numérica. Escribimos$a > b$ (leer$a$ es mayor que$b$) cuando$a$ está a la derecha de$b$ en la recta numérica. Esto se muestra para los números$3$ y$5$ en la Figura$\PageIndex{10}$.

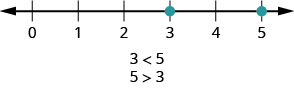
$Esta cifra es una recta numérica con los puntos 3 y 5 etiquetados con puntos. Debajo de la línea numérica se encuentran los estados 3 es menor que 5 y 5 es mayor que 3.$

Figura$\PageIndex{10}$: El número 3 está a la izquierda del 5 en la recta numérica. Entonces 3 es menor que 5, y 5 es mayor que 3.

Las líneas de números a seguir muestran algunos ejemplos más.

$Esta cifra es una recta numérica con los puntos 1 y 4 etiquetados con puntos.$

$4$está a la derecha de$1$ en la recta numérica, entonces$4 > 1$. $1$está a la izquierda de$4$ en la recta numérica, entonces$1 < 4$.

$Esta cifra es una recta numérica con puntos negativos 2 y 1 etiquetados con puntos.$

$-2$está a la izquierda de$1$ en la recta numérica, entonces$−2 < 1$. $1$está a la derecha de$−2$ en la recta numérica, entonces$1 > −2$.

$Esta cifra es una recta numérica con puntos negativos 3 y negativos 1 etiquetados con puntos.$

$−1$está a la derecha de$−3$ en la recta numérica, entonces$−1 > −3$. $−3$está a la izquierda de$−1$ en la recta numérica, entonces$−3 < − 1$.

Ejemplo$\PageIndex{2}$: order the pairs

Ordene cada uno de los siguientes pares de números usando$<$ o$>$:

$14$___$6$
$−1$___$9$
$−1$___$−4$
$2$___$−20$

Solución

Comience trazando los números en una recta numérica como se muestra en la Figura$\PageIndex{11}$.

$Esta cifra es una recta numérica con puntos negativos 20, negativos 4, negativos 1, 2, 6, 9 y 14 etiquetados con puntos.$

Figura$\PageIndex{11}$

Compara 14 y 6.	14___6
14 está a la derecha de 6 en la recta numérica.	14 > 6

Compara −1 y 9.	−1___9
−1 está a la izquierda de 9 en la recta numérica.	−1 < 9

Compara −1 y −4.	−1___−4
−1 está a la derecha de −4 en la recta numérica.	−1 > −4

Compara 2 y −20.	2___−20
2 está a la derecha de −20 en la recta numérica.	2 > −20

Ejercicio$\PageIndex{3}$

Ordene cada uno de los siguientes pares de números usando$<$ o$>$.

$15$___$7$
$−2$___$5$
$−3$___$−7$
$5$___$−17$

Contestar a: $>$
Respuesta b: $<$
Respuesta c: $>$
Respuesta d: $>$

Ejercicio$\PageIndex{4}$

Ordene cada uno de los siguientes pares de números usando$<$ o$>$.

$8$___$13$
$3$___$−4$
$−5$___$−2$
$9$___$−21$

Contestar a: $<$
Respuesta b: $>$
Respuesta c: $<$
Respuesta d: $>$

Encuentra opuestos

En la recta numérica, los números negativos son una imagen especular de los números positivos con cero en el medio. Debido a que los números$2$ y$−2$ están a la misma distancia de cero, se les llama opuestos. Lo opuesto de$2$ es$−2$, y lo contrario de$−2$ es$2$ como se muestra en la Figura$\PageIndex{12 a}$. Del mismo modo,$3$ y$−3$ son opuestos como se muestra en la Figura$\PageIndex{12 b}$.

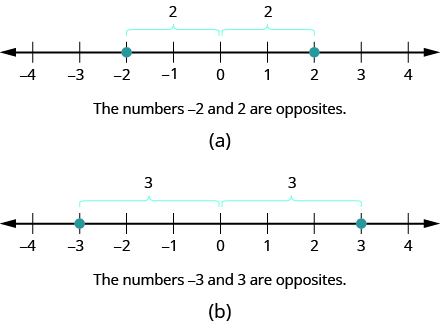
$Esta figura muestra dos líneas numéricas. El primero tiene puntos negativos 2 y positivos 2 etiquetados. Por debajo de la primera línea el enunciado es los números negativos 2 y 2 son opuestos. La segunda línea numérica tiene los puntos negativos 3 y 3 etiquetados. Por debajo de la recta numérica se encuentra la declaración negativa 3 y 3 son opuestos.$

Figura$\PageIndex{12}$

Definición: opuesto

Lo contrario de un número es el número que está a la misma distancia de cero en la recta numérica, pero en el lado opuesto de cero.

Ejemplo$\PageIndex{3}$:

Encuentra lo contrario de cada número:

$7$
$−10$

Solución

El número$−7$ está a la misma distancia de$0$ como$7$, pero en el lado opuesto de$0$. Así$−7$ es lo contrario de$7$ como se muestra en la Figura$\PageIndex{13}$.

$Esta cifra es una línea numérica. Se etiquetan los puntos negativos 7 y 7. Por encima de la línea se muestra la distancia de 0 a negativo 7 y la distancia de 0 a 7 son ambas 7.$

Figura$\PageIndex{13}$

El número$10$ está a la misma distancia de$0$ como$−10$, pero en el lado opuesto de$0$. Así$10$ es lo contrario de$−10$ como se muestra en la Figura$\PageIndex{14}$.

$Esta cifra es una línea numérica. Se etiquetan los puntos negativos 10 y 10. Por encima de la línea se muestra la distancia de 0 a negativo 10 y la distancia de 0 a 10 son ambas 10.$

Figura$\PageIndex{14}$

Ejercicio$\PageIndex{5}$

Encuentra lo contrario de cada número:

$4$
$−3$

Contestar a: $-4$
Respuesta b: $3$

Ejercicio$\PageIndex{6}$

Encuentra lo contrario de cada número:

$8$
$−5$

Contestar a: $-8$
Respuesta b: $5$

Notación opuesta

Así como la misma palabra en inglés puede tener diferentes significados, el mismo símbolo en álgebra puede tener diferentes significados.

El significado específico se vuelve claro al observar cómo se usa. Has visto el símbolo “$−$”, de tres maneras distintas.

10 - 4	Entre dos números, el símbolo indica la operación de resta. Leemos 10 − 4 como 10 menos 4.
-8	Frente a un número, el símbolo indica un número negativo. Leemos −8 como ocho negativo.
-x	Frente a una variable o un número, indica lo contrario. Leemos −x como lo opuesto a x.
− (−2)	Aquí tenemos dos señales. El signo entre paréntesis indica que el número es negativo 2. El signo fuera de los paréntesis indica lo contrario. Leemos − (−2) como lo opuesto a −2.

Definición: Notación opuesta

$−a$significa lo contrario del número$a$.

La notación$−a$ se lee lo contrario de$a$.

Ejemplo$\PageIndex{4}$: simplify

Simplificar:$−(−6)$.

Solución

	− (−6)
Lo opuesto de −6 es 6.	6

Ejercicio$\PageIndex{7}$

Simplificar:$−(−1)$

Contestar: $1$

Ejercicio$\PageIndex{8}$

Simplificar:$−(−5)$

Contestar: $5$

Enteros

El conjunto de números de conteo, sus opuestos, y$0$ es el conjunto de números enteros.

Definición: enteros

Los enteros son números de conteo, sus opuestos y cero.

\[\ldots −3, −2, −1, 0, 1, 2, 3 \ldots \nonumber \]

Debemos tener mucho cuidado con los signos a la hora de evaluar lo contrario de una variable.

Ejemplo$\PageIndex{5}$: evaluate

Evaluar$−x$:

cuando$x = 8$
cuando$x = −8$

Solución

Para evaluar −x cuando x = 8, sustituya x por 8.	$-x$
Sustituto$\textcolor{red}{8}$ por x.	$-(\textcolor{red}{8})$
Simplificar.	$-8$

Para evaluar −x cuando x = −8, sustituya x por 8.	$-x$
Sustituto$\textcolor{red}{-8}$ por x.	$-(\textcolor{red}{-8})$
Simplificar.	$-8$

Ejercicio$\PageIndex{9}$

Evaluar$−n$:

cuando$n = 4$
cuando$n = −4$

Contestar a: $-4$
Respuesta b: $4$

Ejercicio$\PageIndex{10}$

Evaluar$−m$:

cuando$m = 11$
cuando$m = −11$

Contestar a: $-11$
Respuesta b: $11$

Simplificar expresiones con valor absoluto

Vimos que números como$5$ y$−5$ son opuestos porque están a la misma distancia de$0$ en la recta numérica. Ambos son cinco unidades de$0$. La distancia entre$0$ y cualquier número en la línea numérica se llama el valor absoluto de ese número. Debido a que la distancia nunca es negativa, el valor absoluto de cualquier número nunca es negativo. El símbolo para el valor absoluto es de dos líneas verticales a cada lado de un número. 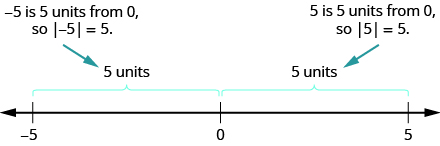Entonces el valor absoluto de$5$ se escribe como$|5|$, y el valor absoluto de$−5$ se escribe$|−5|$ como se muestra en la Figura$\PageIndex{15}$.

$Esta cifra es una línea numérica. Se etiquetan los puntos negativos 5 y 5. Por encima de la recta numérica la distancia de 5 a 0 negativo se etiqueta como 5 unidades. También por encima de la recta numérica la distancia de 0 a 5 se etiqueta como 5 unidades.$

Figura$\PageIndex{15}$

Definición: Valor absoluto

El valor absoluto de un número es su distancia desde$0$ la línea numérica.

El valor absoluto de un número$n$ se escribe como$|n|$.

\[|n| \geq 0\; for\; all\; numbers \nonumber \]

Ejemplo 3.6:

Simplificar:

$|3|$
$|−44|$
$|0|$

Solución

	\|3\|
3 es 3 unidades a partir de cero.	3

	\|-44\|
-44 es 44 unidades a partir de cero.	44

	\|0\|
0 ya está en cero.	0

Ejercicio$\PageIndex{11}$

Simplificar:

$|12|$
$− |−28|$

Contestar a: $12$
Respuesta b: $-28$

Ejercicio 3.12:

Simplificar:

$|9|$
$− |37|$

Contestar a: $9$
Respuesta b: $-37$

Colaboradores y Atribuciones

Template:ContribElementaryAlgebraOpenStax

Para evaluar −x cuando x = 8, sustituya x por 8.	\(-x\)
Sustituto\(\textcolor{red}{8}\) por x.	\(-(\textcolor{red}{8})\)
Simplificar.	\(-8\)

Para evaluar −x cuando x = −8, sustituya x por 8.	\(-x\)
Sustituto\(\textcolor{red}{-8}\) por x.	\(-(\textcolor{red}{-8})\)
Simplificar.	\(-8\)

Search

Ejemplo\(\PageIndex{1}\): plot on the number line

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejemplo\(\PageIndex{2}\): order the pairs

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Definición: opuesto

Ejemplo\(\PageIndex{3}\):

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Definición: Notación opuesta

Ejemplo\(\PageIndex{4}\): simplify

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Definición: enteros

Ejemplo\(\PageIndex{5}\): evaluate

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Definición: Valor absoluto

Ejemplo 3.6:

Ejercicio\(\PageIndex{11}\)

Ejercicio 3.12: